基于交叉延迟线位敏阳极微通道板探测器的光子计数激光三维超分辨成像（特邀）

赵惠，殷浩蒙，2，刘永安，盛立志，杨向辉，邹刚毅，夏思宇，杨明洋，2，樊学武

（1 中国科学院西安光学精密机械研究所，西安 710119）

（2 中国科学院大学，北京 100049）

0 引言

当前，天基态势感知［1-4］以获取目标亮度、几何形状及空间位置等信息为主要目标，未来则以包括距离、位姿及三维形貌等在内的多要素信息获取为重点技术发展方向，而光子计数激光三维成像是典型代表。当前，国内外研究大多集中于基于盖革模式雪崩光电二极管阵列探测器（Geiger Mode Avalanche Photodiode Detector，GM-APD）的光子计数激光三维成像［5-13］。美国麻省理工学院林肯实验室在GM-APD 光子计数激光三维成像领域处于领先地位，自1998 年起先后研制Gen 系列三代样机［14-17］，证明了GM-APD 探测器的潜力。此外，英国、日本、德国、瑞士等也积极推进研究工作，尤其是赫瑞瓦特大学实现的千赫兹超高速、亚厘米距离分辨三维成像令人瞩目［18-26］。

国外之所以在光子计数激光三维成像领域处于领先地位，根本原因在于掌握了GM-APD 探测器的核心技术。除美国林肯实验室之外，包括美国弗吉尼亚大学奥斯汀分校［27］、英国爱丁堡大学［28］、瑞士洛桑联邦理工学院［29］、意大利米兰理工学院［30］等都已成功研发了较大面阵GM-APD 探测器，但高等级器件对国内禁售。反观国内，包括中电44 所［31］、中科院半导体研究所［32］以及北方夜视集团等均在开展GM-APD 探测器研发，但尚未实现原位替代。因此，针对其他类型光子计数探测器的激光三维成像有研究价值，位置敏感微通道板（Micro Channel Plate，MCP）阳极探测器就是其中之一。

国外很早就将位敏阳极MCP 探测器应用于空间探测。如1989 年，美国国家航空航天局（National Aeronautics and Space Administration，NASA）发射探空火箭使用MAMA 型阳极探测器收集银河系NGC6240 星的紫外数据［33］。1995 年，美欧合作的SOHO 任务使用延迟线阳极探测器研究日冕加热过程［34］。2001 年，J-PEX 高分辨率光谱仪使用Vernier 型阳极探测器研究白矮星G191-B2B 的光谱［35］。2012 年，日本EXCEED 卫星则使用电阻型阳极探测器进行空间观测［36］。西安光机所自2007 年开始，针对空间科学应用，先后研制出楔条形探测器原理样机、Vernier 阳极探测器以及大尺寸交叉延迟线阳极探测器；之后以此为基础又开展了MCP 阳极探测器在紫外、可见、近红外波段的光子计数三维成像研究［37-42］。

近年来，国外在积极探索位敏阳极MCP 探测器用于空间目标成像的可行性［43］，提出了利用MCP 位敏阳极探测器实现空间目标三维成像的构想，仿真研究了其在千公里距离上针对低轨卫星实施三维成像的潜力［44］。因此，本文立足于自研大尺寸交叉延迟线位敏阳极MCP/CDL（Micro-Channel-Plate with Cross-Delay-Line，MCP/CDL）探测器，通过开展理论机理研究、仿真特性分析、重建算法研发、探测器样片试制以及三维成像试验等全方位研究，打通了基于MCP/CDL 探测器的光子计数激光三维成像技术体制，在持续改进提升探测器硬件性能的同时，还将多通道探测、多域联合及软性距离选通可控延迟等引入三维重建，探索能够突破时空分辨能力的三维超分辨重建的可行性。

1 MCP/CDL 探测器光子计数机理与激光三维成像方案构想

位敏阳极MCP 探测器主要由输入窗、光电阴极、MCP 组、Ge 感应层以及位敏阳极收集器等部件构成，如图1（a）所示。其中，常见的位敏阳极主要有电阻阳极、楔条形阳极、Vernier 阳极、交叉条阳极以及延迟线阳极等。与其他类型的阳极收集器相比，延迟线阳极收集器具有结构紧凑、计数率高且时间分辨能力强的特点。具体而言，延迟线阳极的时间分辨能力可以达到皮秒量级，而计数率最大可达兆赫兹以上，同时还可以做到比如直径50 mm 的较大尺寸。因此，基于延迟线阳极收集器的大尺寸位置敏感MCP/CDL 探测器在高时间分辨和高空间分辨的场合应用较多，特别适合作为光子计数激光三维成像系统的核心关键器件。

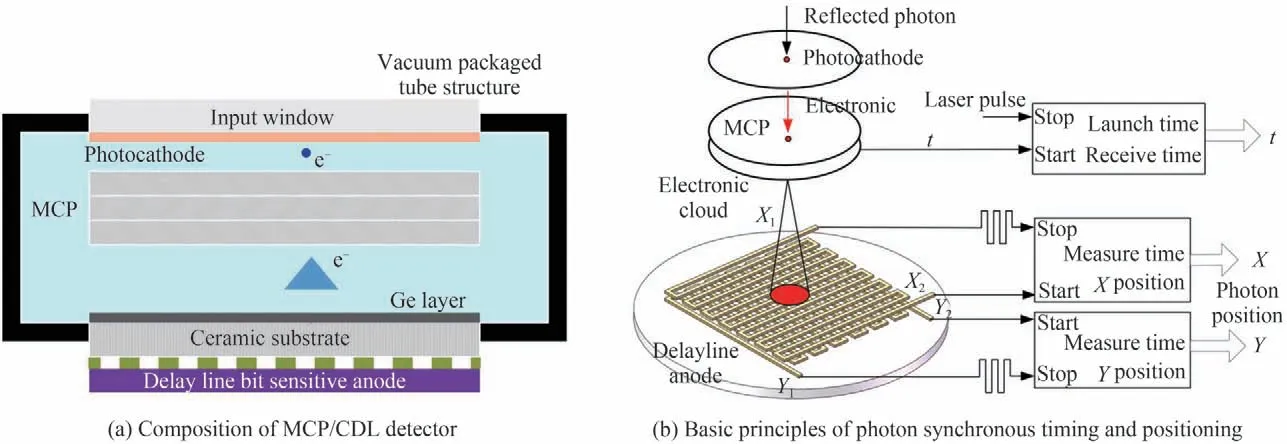
图1 交叉延迟线位敏阳极MCP 探测器组成及光子同步计时与定位基本原理Fig.1 The composition of the crossed delay line position-sensitive anode MCP detector and the basic principle of photon synchronization timing and positioning

位敏阳极MCP/CDL 探测器工作过程如图1（b）所示，光子到达光电阴极后首先在阴极以一定的量子效率激发出初始光电子，之后光电子进入MCP 通道产生电子倍增。经过级联的MCP 倍增后输出电子云团，然后经过电场加速后撞击在位敏阳极上，再由位敏阳极上相互交叉绝缘的延迟线收集后输出电荷脉冲信号。通过对到达探测器的光子的到达时间和位置数据的同步获取就可以得到目标回波三维点云信息。其中，光子到达时间t基于飞行时间法测量，由针对探测器输出脉冲的高精度计时获得，如图2（a）所示，通过统计信号脉冲与参考脉冲之间的脉冲周期个数与延迟进行测算；而利用延迟线收集技术实现光子到达位置二维坐标位置的原理如图2（b）所示。可以看到，每个电子云团所携带的电荷首先由两条相互垂直的延迟线收集，随后沿着延迟线两端传播，最后根据电荷脉冲达到延迟线两端的延时差就可以计算出电荷脉冲到达延迟线的位置，从而实现空间二维位置（x，y）分辨。

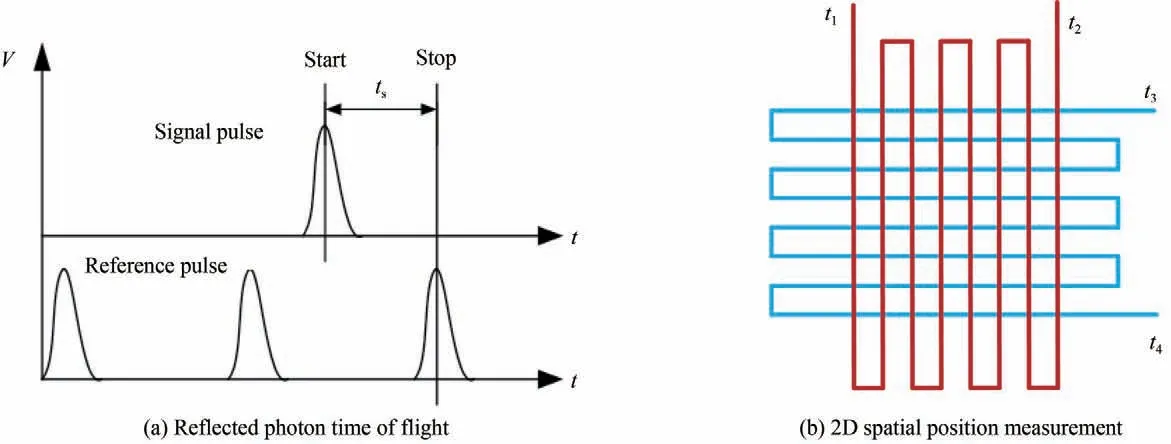
图2 回波光子飞行时间及二维空间位置的测量机理Fig.2 Measurement mechanism of reflected photons on flight time and two-dimensional space position

通过如图2 所示的光子同步计时与定位技术能够获得每一个目标回波光子的（x，y，t）三维点云信息，为实现光子计数激光三维成像奠定了基础。因此，根据延迟线位敏阳极（MCP/CDL）探测器的光子计数机理，对应的光子计数激光三维成像系统方案如图3 所示。该系统在空间应用时，既可以采用单基模式，即激光发射端和光子计数三维成像系统接收端位于同一卫星平台上，也可以采用双基模式，即发射端和接收端分别位于两个独立的卫星平台上。首先，使用高重频、窄脉宽、低功耗的脉冲激光器经发射望远镜准直扩束后对目标进行照明；之后，使用中等口径的望远镜系统收集目标回波光子，并依靠交叉延迟线位敏阳极MCP/CDL 探测器对到达光子进行同步计时与定位来获得目标回波点云数；最后，针对回波点云实施重建来完成三维成像。

图3 基于MCP/CDL 的光子计数激光三维成像方案构想Fig.3 Conception of photon counting laser 3D imaging scheme based on MCP/CDL

2 MCP/CDL 光子计数激光三维成像的端到端成像仿真分析

2.1 基于激光雷达方程的光子计数成像建模

激光雷达方程是针对光子计数激光三维成像实施量化评价的重要手段。通常，要求激光远场照明光斑远大于目标尺寸，针对空间目标，不考虑大气传输衰减，给出了这种典型工况下的激光雷达方程［45］，激光回波功率Pr为

此外，考虑到激光脉冲能量在时间和传输截面上的分布是不均匀的，以高斯激光脉冲为例，激光能量在传输过程中的时间和空间分布可表示为

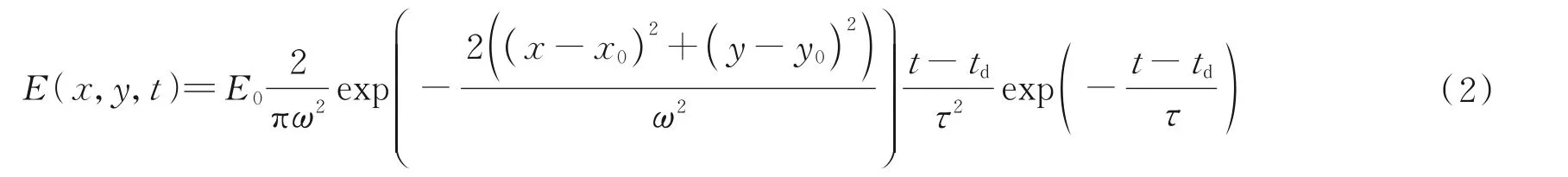
式中，E0表示激光脉冲能量，量纲为J；（x0，y0）表示目标位置处激光传输截面中心位置，量纲为m；td代表回波到达时间，量纲为s；τ表示激光的形状，其与脉宽pω的关系可以近似表示为pω=3.5τ；脉宽pω的量纲为ns。脉冲激光雷达焦平面接收到的单脉冲回波能量Erp可表示为

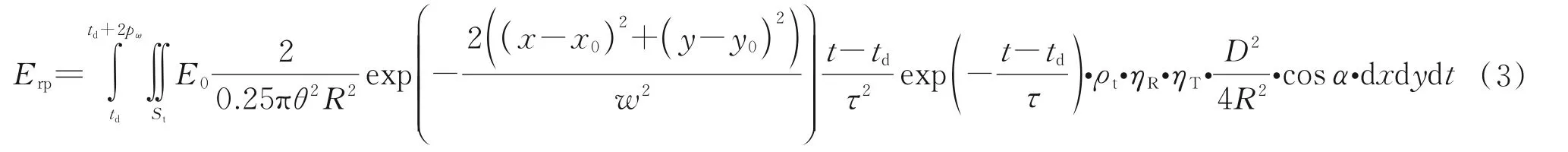
由式（3）可以看到，探测器接收到的回波能量Erp分别与激光发射能量E0成正比，与距离R的4 次方成反比，与光学系统口径D的平方成正比，与激光发散角θ的平方成反比，与目标面积St成正比，此外还与发射端光学系统透过率ηT、接收端光学系统透过率ηR、目标被照表面与目标位置处光束截面的夹角α等因素有关。

光子计数激光三维成像系统是通过统计并累计目标回波光子流实施概率探测成像的，所以回波光子数的数量及分布是其主要特征。利用式（3）所给出的激光雷达方程根据光子能量量化就能够计算出探测器的回波光电子数rph，即

式中，ηq为探测器量子效率；h为普朗克常数，h=6.62×10-34J·s；υ为光频率，量纲为Hz；hυ表示单个光子能量。

MCP/CDL 探测器平均响应数可以表示为

式中，rb为背景噪声光电子数，nd为探测器暗计数；探测器输出光电子数Nout可以表示为Nout=MNph；M代表MCP/CDL 探测器的增益，由于具有高达106以上的增益，所以MCP/CDL 探测器可以响应极其微弱的回波。

探测概率是决定目标光子是否被界定为信号光子的依据。首先，MCP 探测器在进行光子计数成像时，每个虚拟像素由多个倍增通道组成，而每个倍增通道的光电倍增过程都可以认为是相对独立的泊松过程，同时多个独立泊松过程的和仍然符合泊松分布；其次，探测器接收的光子除了包含目标回波对应的有效信号光子之外，还包括背景噪声及暗电流噪声等激发的等效噪声光子，而这些噪声光子也近似服从泊松分布。另外，MCP/CDL 探测器采用位敏阳极结合定时模块探测并记录回波光子三维数据信息，由于延迟线阳极一次仅能解码一个时空位置，当同时有多个位置探测到光子时就会出现误码情况。因此，当多个像元均对应相同的目标距离时，每个像元时隙内探测到光子的概率可表达为

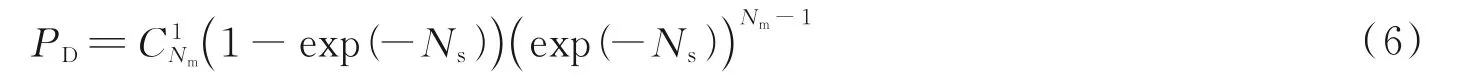
式中，Nm为相同目标距离像元个数，Ns为探测器每个等效像元接收到的平均回波光电子数，式（6）通过对单脉冲回波进行分析，实现对系统激光发射能量和可适用背景光强范围的初步估计；对于非相同时刻但到达时间很接近的两个或多个光子，由于探测器死时间影响，探测器只能探测到第一个光子，因此，实际应用中，第i个时隙探测到光子的概率等于前（i-1）个时隙未探测到光子概率与第i个时隙探测到光子概率的乘积，在弱光环境下，单个脉冲发生两个或多个光子事件的概率特别小时，每个时隙发生光子事件的概率可近似认为服从独立的泊松分布。

由图4（a）可知，每个像素回波光电子数过多或过少都会导致探测概率下降，且探测概率峰值随着相同目标距离像元数的增大，相应的向单像素回波光子数小方向偏移，从图4（b）中可以看出在焦面总回波光电子数为定值时，探测概率会随着相同目标距离像元数的增大逐渐减小且趋于定值。这是由于随着像元数增大，单个像元分到的光电子数越少，相同目标距离对应像元之间的探测串扰会减小，相对来说像元总回波光电子数越少，光子到达时间和位置更随机，像元之间的串扰就会越小。

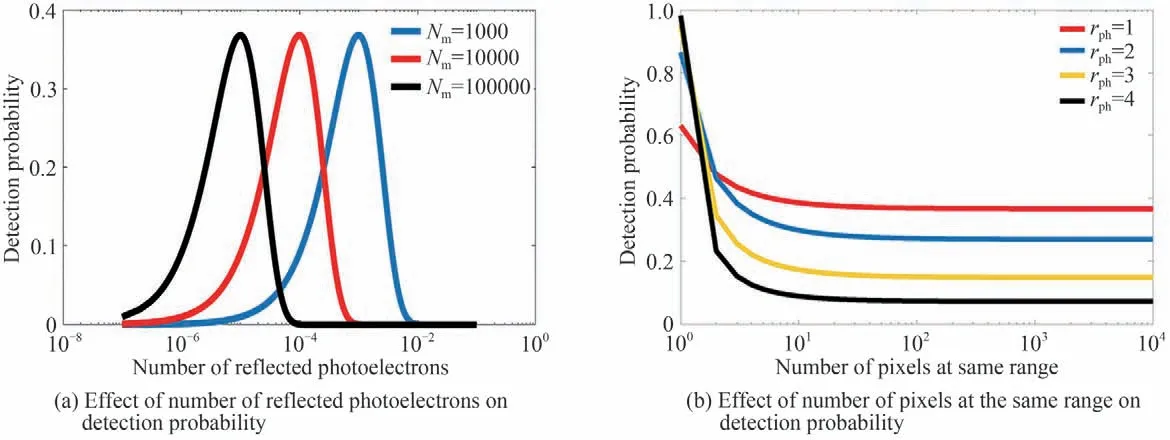
图4 回波光电子数及相同目标距离像元数对探测概率的影响Fig.4 Effect of the number of reflected photoelectrons and pixels at the same height on the probability of detection

成像信噪比是光子计数成像系统的重要指标，与回波光子数密切相关。对于MCP/CDL 探测器而言，其自身的暗计数率极低可以忽略不计，在回波光子水平一定的条件下，成像信噪比主要受背景辐射光子数的影响。式（7）与式（8）分别给出了背景辐射光子数及信噪比计算公式。其他参数保持不变，典型背景辐照条件（比如Eb为3.6×10-6W·m-2·nm-1）下，令窄带滤光片带宽Δλ为1 nm，接收光学系统孔径D为0.6 m，那么当天顶角θ及照射方向与目标被照射面法线夹角θi均为0°时，可以得到不同累积探测次数下信噪比变化情况，如图5 所示。显然，增加回波信号光电子数或者增加发射脉冲数（积分时间），均可以有效提升成像的信噪比。

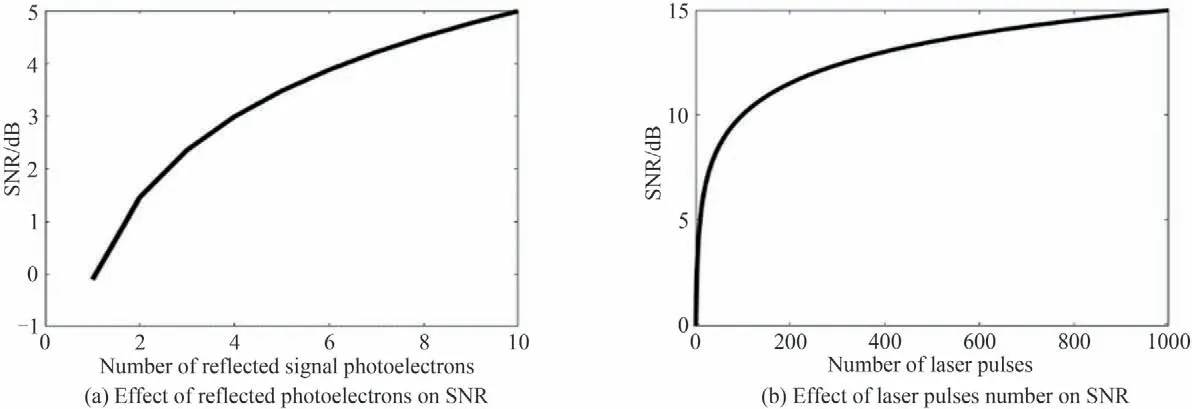
图5 信噪比随信号光电子数和发射脉冲数的变化情况Fig.5 The variation of signal-to-noise ratio with the number of signal photoelectrons and number of laser pulse

式中，rb为背景光电子数；Δλ为窄带滤光片带宽，量纲为nm；Eb为背景辐照度，量纲为W·m-2·nm-1；θ为天顶角，量纲为rad；θi为照射方向与目标被照射面法线夹角，量纲为rad；t为积分时间，量纲为s。

测距精度与回波信号强度、激光脉冲宽度、背景噪声等都有关系，采用参数估计方法对最大似然估计模型下的测距精度进行分析。首先假设目标距离分布一致，相邻像素及其不同时隙探测到光子事件的概率均服从独立的泊松分布；然后将目标距离作为估计量，回波光子飞行距离作为随机量；最后通过克拉美-罗下界（Cramer-Rao Lower Bound，CRLB）计算无偏估计量所能达到的最小方差，方差越小，估计越准确，精度越高。综上，光子计数激光三维成像目标距离的CRLB［46］可表示为

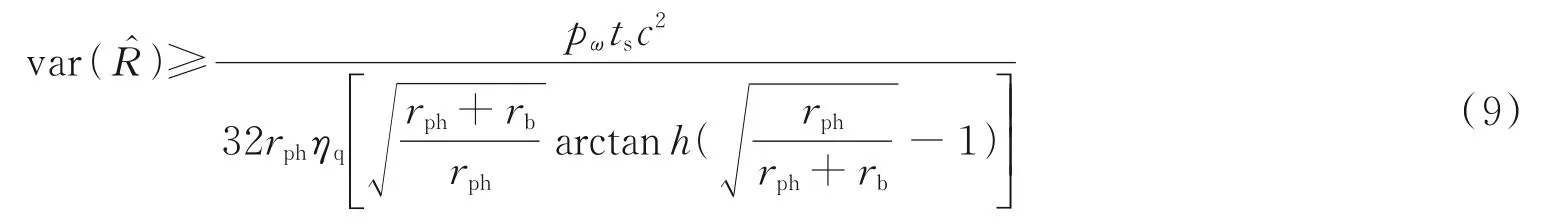
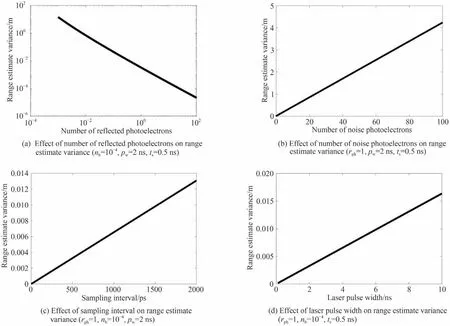
图6 距离估计方差与其影响因素变化曲线Fig.6 Variance curve of distance estimation variance and its influencing factors

2.2 基于蒙特卡罗的端到端成像仿真分析

在2.1 节进行解析建模的基础上，采用蒙特卡罗开展端到端的全链路成像仿真分析，如图7 所示。

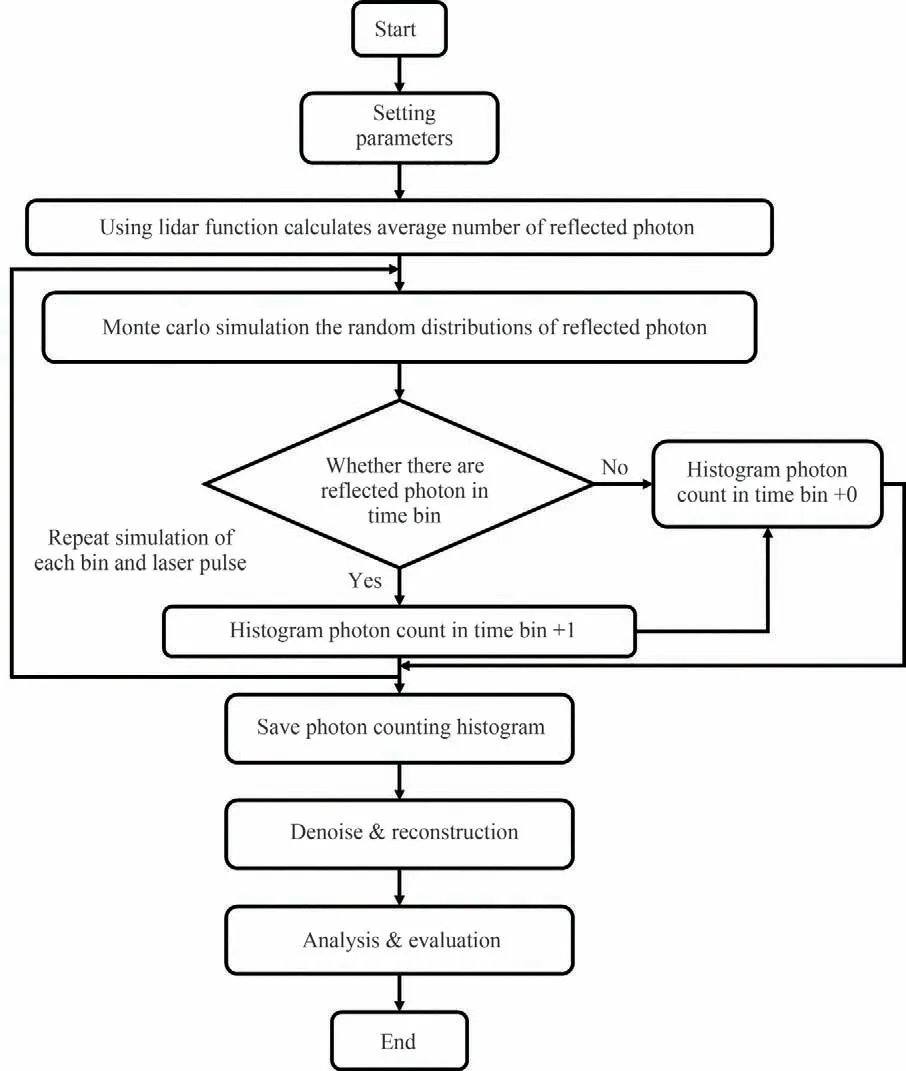
图7 端到端蒙特卡罗法仿真流程Fig.7 End-to-end Monte Carlo simulation process

以图8（a）所示空间目标（目标姿态以前视场为例，目标表面法线与接收光学系统光轴平行，将与前表面平行且过目标最远点的面作为零距离平面，此时目标相对距离分布如图8（b）所示）考察不同工况下的光子计数激光三维成像性能。其中，光学系统口径依然为0.6 m，焦距为6 m，F#为10，探测器像元大小为60 μm，靶面大小为256×256 个像元，532 nm 激光单脉冲能量为1 mJ，重频为10 kHz，激光发散角为2.6 mrad，探测时隙数为100 个，探测时隙宽度为0.5 ns，背景辐照为3.6×10-6W·m-2·nm-1，窄带滤光片带宽为1 nm，不同积分时间与不同作用距离对应的光子计数三维成像效果图8（c）与图8（d）所示。

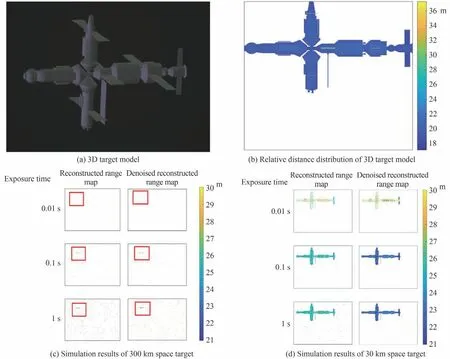
图8 3D 空间目标端到端仿真示例Fig.8 3D space target end-to-end simulation example

可以看到，全链路仿真成像能够实现对目标形貌的三维刻画。同时，在作用距离一定的情况下，增加积分时间能够有效提升成像信噪比。因此，基于蒙特卡罗法的端到端仿真成像是有效的。在开展成像仿真的同时，对背景辐照对测距精度的影响同步进行了分析，如图9 所示。背景辐射对应的噪声较大时，测距精度的主要影响因素是噪声，其主要原因是当门限内的信号回波光电子数量一定时，噪声光子的增加会将回波信号脉冲淹没在噪声中，且当噪声光子数过大时同时探测门开启后，探测器探测到噪声光子后进入死时间，探测到信号光子概率会大大减小，从而导致回波光子分布直方图峰值前移或者峰值消失，但随着噪声的逐渐减弱，测距精度将趋于一个常数。

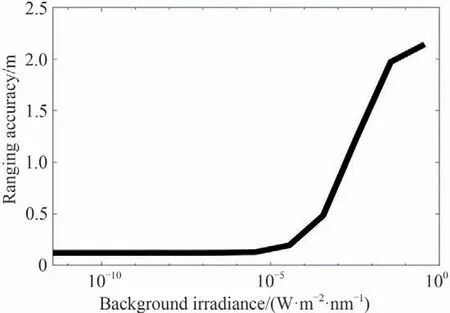
图9 背景辐照与测距精度之间的关系Fig.9 The relationship between background irradiance and ranging accuracy

3 强度-时间-空间多域联合超分辨三维重建

尽管光子计数探测器具有极高的光子灵敏度，但是普遍存在像素间隔大、集成度不够高等问题，比如MCP/CDL 探测器目前的空间分辨仅为60 μm 左右，与传统CCD 或CMOS 探测器相比差距较大，导致光子计数三维成像的空间分辨率不高，距离图像表现为严重的马赛克效应。另外，光子计数探测器的时间分辨能力主要受时间分辨电子学计时时隙的限制，目前研制的MCP/CDL 探测器的时间分辨能力可优于78 ps。因此，通过改进探测器的硬件水平提升光子计数激光三维成像系统的时间与空间分辨率是重要研究方向，但是本文将重点探讨协同工作模式下通过先进回波处理算法实现时空超分辨的可行性。

3.1 基于强度图引导距离图上采样的空间超分辨

在前期的研究中，为了消除光子计数成像因回波脉冲与发射脉冲难以一一对应带来的距离二义性问题，提出了一种利用强度图像边缘高频信息作为约束，通过迭代优化改善距离二义性的算法，可以将距离方差减小二分之一以上［41］。实际上，这种方式同样可以用来提升光子计数激光三维成像距离数据的空间分辨率。2020 年，爱丁堡大学GYONGY I和赫瑞瓦特大学HALIMI A 等采用总广义变分（Total Generalized Variation，TGV）强度图像引导距离图像上采样的方案将距离图的空间分辨率提升了4倍［23］。2020年，中国科学技术大学黎正平等采用亚像素扫描方式将8.2 km 处采集的8 幅亚像素扫描图像融合，将分辨率提升到系统瑞利分辨的两倍［12］。2020年，哈尔滨工业大学龚道然等采用双光路方式，一路由高分辨ICCD 采集获得高空间分辨的强度图，另一路由低分辨率GM-APD 采集获得低分辨距离图，分别采用双三次插值、引导滤波和TGV 等几种强度引导上采样算法获得超分辨距离图像，证明了强度引导上采样方案在光子计数三维超分辨距离图像的潜力，并对TGV 强度引导上采样方案进行了优化［47］。2021年，中科院西安光机所薛瑞凯等采用GM-APD 对3 m 处目标进行成像，通过采用衍射光学元件与亚像素扫描成像方式将单光子三维系统空间分辨率由3 mm 提升到0.33 mm［48］。

如图10（a）所示，本文针对MCP/CDL 探测器光子计数激光三维成像的特点，在前期研究的基础上提出了基于强度上采样的空间分辨率提升算法。首先，将选定积分时间之内的回波点云数据通过统计方式获得原始距离图像；其次，将原始距离图像通过上采样方式转化成与高分辨率强度图大小相同的稀疏高分辨距离图，其中高分辨率强度图像由共孔径协同观测模式同步获得；再次，以全零图像作为待求解高分辨率距离图像的初始估计，以稀疏上采样高分辨距离图与待求解高分辨率距离图之间的差值作为保真项，而以广义全变分作为正则项来构建目标函数；最后，计算高分辨强度图像各向异性张量，并将该张量作为一阶正则项系数引导原始分辨距离图图像上采样过程，通过迭代优化获得空间分辨率提升的距离图像。图10（b）给出了强度引导距离图上采样提升距离图空间分辨率的示例，超分倍率为4 倍。可以看到，距离图的空间分辨率得到了明显的改善。因此，只要采用共孔径设计方式同步获取高分辨率强度图像与光子计数距离图像，就可以突破光子计数探测器本身分辨率不够对空间分辨的影响。

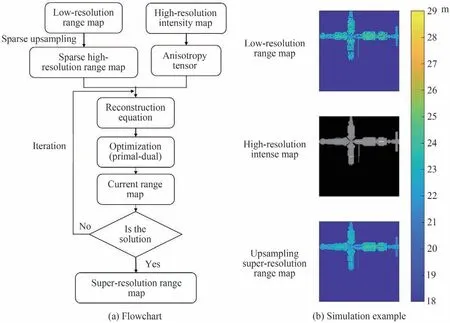
图10 基于强度引导距离图上采样的空间超分辨流程及仿真示例Fig.10 Flowchart and simulation example of spatial super-resolution based on intensity-guided depth upsampling

3.2 基于软性距离选通主动延迟亚时间精度距离超分辨

从理论上来讲，3.1 节所示的距离图像空间超分辨成像方案同样可以用于光子计数激光三维成像系统空间分辨率的提升，但是如何使用超分辨方法提升光子计数激光三维成像系统的测距精度却鲜有研究，而测距精度恰恰是三维成像系统成像质量最重要的参数，尤其是在远距离成像场景下，因此本文将亚像素高分辨成像方案应用于时间维，提出了亚时间分辨扫描方案。

如图11 所示，通过将开始门限延迟固定相位采集多幅连续低时间分辨距离数据，对采集的数据在时间维度通过亚像素融合方式获得具有更多细节的时间信息光子时间分布直方图，配合已有的重构算法，可以通过亚像素超分辨成像方式实现超越探测器硬件限制的高空间分辨和高测距精度三维重建结果。分别采用Middlebury 数据集和3D 空间目标模型进行仿真验证，将数据集中的场景等比例放缩到0～1 m 范围内，采样模块时间分辨设置为1 ns，仿真结果如图12（a）所示。从Middlebury 数据集仿真结果来看，随着延迟间隔Δt越来越小，采集获得信号的时间信息就越多，三维重建后图像的精度越来越高，均方根误差（Root Mean Square Erro，RMSE）越来越小。当延迟间隔为时间分辨的1/100 时，距离图像的均方根误差减小了79.2%；在对3D 模型仿真时，将采样模块时间分辨设置为2 ns，将延迟间隔设置为时间分辨的1/20 倍，重建结果如图12（b）所示，此时获得的超分辨距离图像均方根误差减小了51.9%。除采集模块时间分辨能力外，重建误差还会受到激光脉宽、回波在时隙中的位置等其他因素影响，因此亚时间分辨延迟扫描重建延迟间隔大小与误差减小倍率的精确关系，以及该方案能否减小其他因素对误差的影响还有待深入研究。

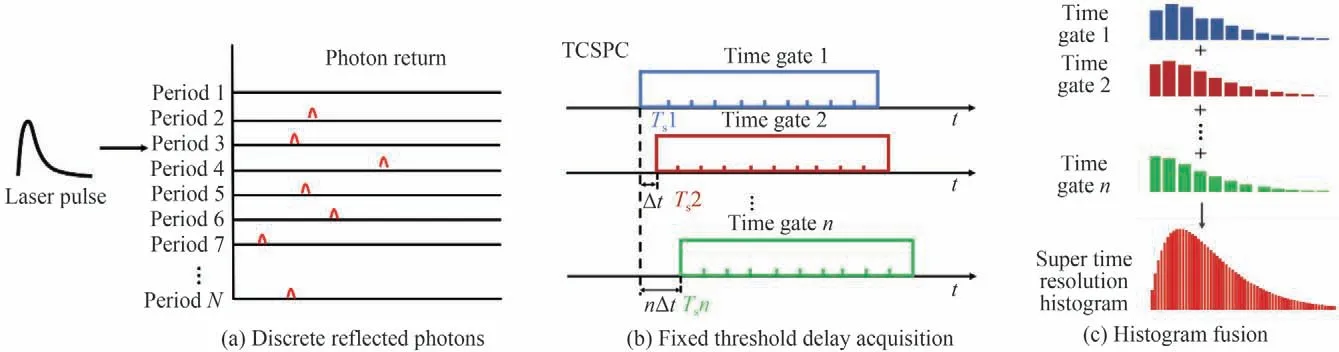
图11 亚时间分辨延迟扫描超分辨重建原理示意图Fig.11 Schematic diagram of the super-resolution reconstruction principle of sub-time-resolved delayed scan

图12 亚时间分辨扫描超分重建仿真示例Fig.12 Sub-time-resolved scanning super-resolution reconstruction simulation example

4 基于MCP/CDL 的光子计数激光三维成像试验研究

4.1 MCP/CDL 探测器样片研制及性能测试

MCP/CDL 探测器主要由输入窗、光电阴极、MCP 组、Ge 感应层以及延迟线位敏阳极收集器等部件构成。探测器中，输入窗采用可见至近红外透过率均较高的石英玻璃；光电阴极采用红外延伸型S25 多碱阴极；同时为了保证较高的增益，采用三块级联的MCP 进行二次电子倍增。图13 为真空封装光子计数成像探测器管体，以及管体与延迟线阳极装配完成后的实物照片。经过测试，研制的MCP/CDL 探测器样片的指标如表1 所示，后续还具备进一步提升和改进的空间。

图13 MCP/CDL 探测器实物Fig.13 MCP/CDL detector

表1 探测器主要技术指标实测结果Table 1 Measured results of main technical indicators of the detector

4.2 光子计数激光三维成像试验

利用研制的MCP/CDL 探测器样片搭建了演示验证原理样机并进行了初步的光子计数激光三维成像试验。图14 所示为研制的基于MCP/CDL 探测器的光子计数激光三维成像系统的原理样机及试验场景。其中，激光发射组件采用由长春新产业光电技术有限公司研制的全固态二极管泵浦Nd∶YAG 激光器（MPL-N-532 nm-100 μJ-19071229），而镜头则采用商用Nikon 70～300 mm 变焦镜头。

图14 MCP/CDL 光子计数激光三维成像系统原理样机及试验场景Fig.14 Principle prototype and test scene of MCP/CDL photon counting laser 3D imaging system

光子计数激光三维成像试验基本原理如图15 所示。通过半透半反镜抽取一小部分发射激光照射在单元APD 探测器上作为计数模块的计数起始信号，获取起始时间t1，由此实现激光发射与时间相关单光子计数（Time-Correlated Single Photon Counting，TCSPC）模块的同步，可以消除外激发同步信号抖动引起的同步性降低问题。为了调试后端电子学和相关处理软件并优化TCSPC 测试精度，首先完成时间测量精度。之后将距离信息与二维图像信息融合，由此形成三维数据。

利用图15 所述系统，在8 m 的距离处对具有不同高度差的目标进行了光子计数三维成像。图16 给出了第一组成像结果。可以看到，系统能够轻松地将距离成像系统不同距离的目标区分出来。此时，两个目标表面之间的距离为40 cm，远远大于MCP/CDL 探测器的计时精度，因此对系统三维成像能力的验证是不充分的。因此，为了进一步验证系统的三维成像能力，开展了第二组成像试验。

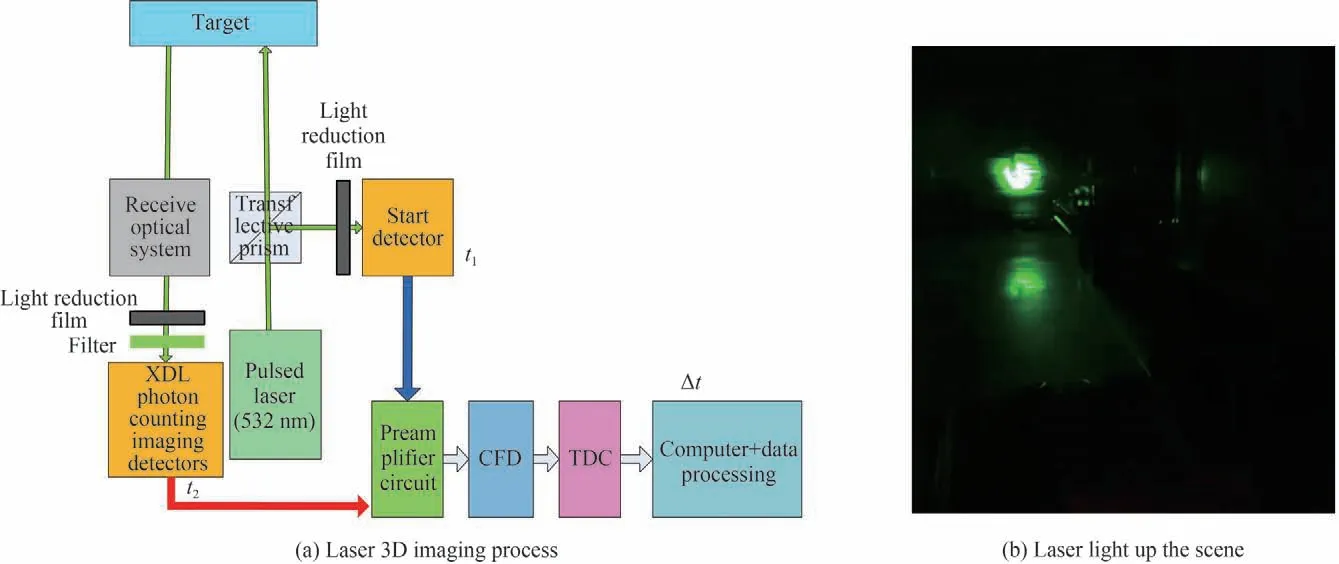
图15 激光三维成像工作流程及激光发射后的场景Fig.15 Laser 3D imaging workflow and scene after laser launch

图16 第一组光子计数激光三维成像试验Fig.16 The first group of photon counting laser 3D imaging experiments

第二组实验基于已有的扫描方式TCSPC 三维成像雷达系统进行［26］，利用研制的CDL 光子计数成像探测器及搭配的光学接收镜头探测目标的回波光子信息。实验系统组成框图如图17 所示，主要由脉冲激光器、发射光学系统、扫描振镜及控制系统、接收光学系统、研制的光子计数成像探测器、TCSPC 电路模块以及计算机控制与数据处理等构成。

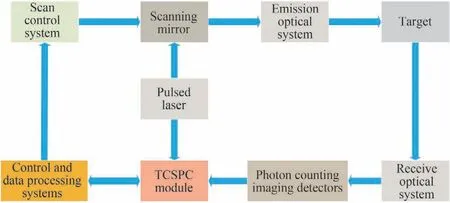
图17 扫描方式激光三维雷达系统框图Fig.17 Scanning mode laser 3D radar system block diagram

测试实验在暗室环境中进行，系统中激光器输出脉冲重复频率设置为10 kHz，扫描像素数目为100×100，通过扫描TCSPC 三维成像雷达系统获得的目标三维成像结果如图18 所示。可见，采用研制的MCP/CDL 光子计数成像探测器成功获取了目标的三维信息。根据所搭建实验系统的性能，在目标距离6.8 m 时，实现了优于5 mm 的距离分辨。

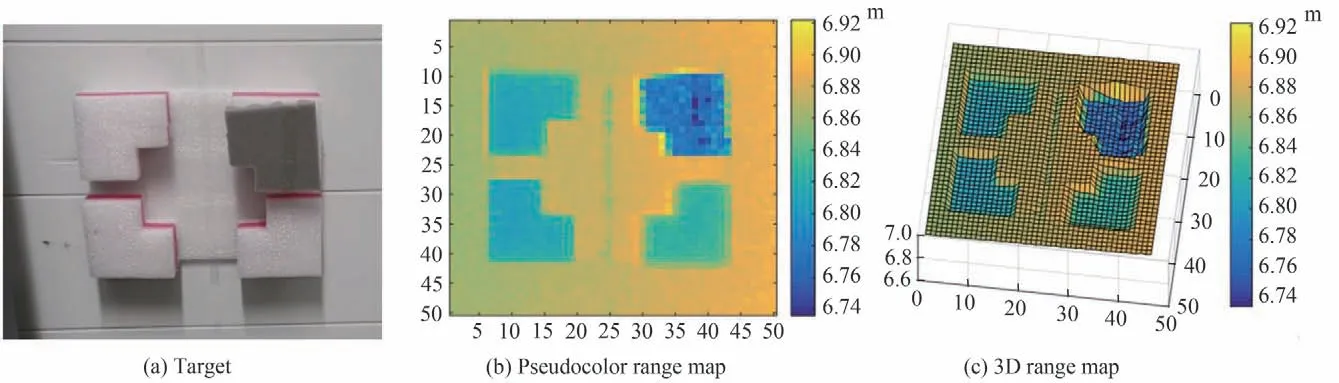
图18 实验采用的测试目标及三维成像结果Fig.18 The target used in the experiment and the 3D imaging results

5 结论

本文依托自主研制的交叉延迟线位敏阳极MCP/CDL 探测器，提出了一种光子计数激光三维超分辨成像技术，详细介绍了该技术成像机理、全链路建模与仿真特性分析、可突破时空分辨硬件限制的三维超分辨重建算法，并对探测器样片原理样机进行了试验验证。研究表明：基于MCP/CDL 探测器的光子计数激光三维超分辨成像技术具备在远距离获得高时空分辨三维图像的潜力，是值得进一步探索的可服务于天基态势感知目标精细成像的技术途径。但是，由于需要光子累积，目前系统的成像时间较长，一般在十几分钟量级。接下来将从持续提升包括时空分辨率、成像速率等在内的探测器性能，及改进超分辨重建算法两方面进行研究，为远距离小目标的精细三维成像奠定基础。

致谢感谢中国科学院西安光学精密机械研究所瞬态光学与光子学国家重点实验室张同意老师和康岩老师提供的大力协助。