基于博弈论抗共谋攻击的全局随机化共识算法

张宝，田有亮，高胜

基于博弈论抗共谋攻击的全局随机化共识算法

张宝1,2，田有亮1,2，高胜3

（1. 贵州大学计算机科学与技术学院，贵州 贵阳 550025；2. 贵州省公共大数据重点实验室，贵州 贵阳 550025；3. 中央财经大学信息学院，北京 100081）

随着区块链技术的不断发展，作为区块链技术基石的共识技术受到更多关注，共识技术的发展越发迅速，但依旧存在相关难题。容错类共识算法作为区块链共识技术的代表性之一，依然存在诸多难题待研究，针对容错类共识算法中节点随机性和节点共谋攻击问题进行了研究，提出基于博弈论抗共谋攻击的全局随机化共识算法，通过实现节点的随机化和解决相关安全问题提高区块链网络的安全性和吞吐量。在选择参与容错类共识算法的节点过程中，利用映射函数和加权随机函数实现发起者和验证者节点的全局随机化，从而保证发起者和验证者节点的身份匿名，提高区块链网络的安全性。利用信誉更新模型实现信誉动态更新的同时利用博弈论分析容错类共识算法的安全问题，构造更加正确和高效的算法模型以提高算法的吞吐量并分析发现这类算法中存在超过1/3节点的共谋攻击问题，利用精炼贝叶斯博弈构造共谋合约，分析求得共谋者之间的纳什均衡点，从而解决超过1/3节点的共谋攻击问题。通过安全性分析和实验表明，基于博弈论抗共谋攻击的全局随机化共识算法相对工作量证明（PoW，proof of work）、权益证明（PoS，proof of stake）和实用拜占庭容错（PBFT，practical Byzantine fault tolerance）共识算法不仅提高吞吐量、降低计算资源消耗，而且该算法抵抗分布式拒绝服务（DDoS，distributed denial of service）、Eclipse attacks和超过1/3节点共谋攻击。

共识算法；全局随机化；博弈论；共谋攻击

0 引言

随着区块链技术的发展，对数据上链速度的要求越来越高，用高效且安全的共识协议来保证数据上链成为区块链系统的关键问题。在该背景下，如何解决基于工作量证明（PoW，proof of work）[1]和基于权益证明（PoS，proof of stake）的共识协议[2]中高资源浪费、低效率上链[3]、权益过大、富者越富、易分叉、易双花[4]等问题是重点。近年来，代理权益证明（DPoS，delegated proof of stake）[5]被认为是解决资源浪费、权益过大和低效率等问题的有效技术。该技术是一种基于投票选举的共识算法，只需要少部分的节点就能达成共识实现交易数据快速上链。基于拜占庭容错协议的Tendermint[6]和True Decentralization[7]协议的出现不仅保证了1/3节点的容错，而且只需要少部分节点对交易进行验证就可以达成最后的共识。

文献[8]提出了一种将PoW和PoS相结合的共识协议，该协议提供了更高的安全性和效率。文献[9]研究了交互式的PoS共识算法，将通信引入块，减少交互，提高效率和安全性，但该协议依然没有解决PoS存在的权益过大、易分叉和易双花问题。文献[10]利用Kgmedoids聚类算法根据参与区块链共识的大规模网络节点的特征进行聚类与层次划分，再将改进的多中心化实用拜占庭容错算法应用于这种聚类后的分层模型。文献[11]研究了新的共识算法固定验证器，但它依赖于极端信任的假设。文献[12]提出了一个无发起者、完全异步的拜占庭容错共识协议。文献[13]提出了一个委托随机拜占庭容错共识协议。文献[14]利用博弈论和智能合约解决了委托计算中不诚实双方的共谋问题。文献[15]提出了休眠共识（SC，sleepy consensus）机制，该机制只要在线诚实节点超过故障节点就可以保证安全性。文献[16]基于发起者的拜占庭容错复制协议提出了HB-BFT（honey badger of BFT）。文献[17]基于拜占庭提出了一种新的共识机制Proteus，无论网络中出现多少次故障，Proteus都能保证稳定的性能。

基于拜占庭容错的这类共识算法中，当提议者提出新块后，发起者接收到提议者指令后开始选择验证者，当验证者确定后由验证者投票达成最终的共识。共识的过程中实现参与节点的随机化是保证共识算法安全性的关键难题。而本文提出的基于博弈论抗共谋攻击的全局随机化共识算法（GRCACAGT，global randomized consensus algorithm resist collusion attack based on game theory）可以解决节点的全局随机化问题以及这类算法中存在的共谋攻击，主要贡献如下。

1) 提出GRCACAGT，利用映射函数和加权随机函数实现共识算法中发起者节点的随机化。

2) 分析容错类共识算法发现1/3节点共谋攻击问题，并利用智能合约和贝叶斯博弈构造共谋合约解决了该问题。

3) 安全性分析和实验表明，GRCACAGT不仅抗分布式拒绝服务（DDoS，distributed denial of service）、1/3节点共谋等攻击，而且相比其他的共识算法，吞吐量和效率方面都有优势。

1 本文算法

本文基于True Decentralization[7]提出GRCACAGT，GRCACAGT与True Decentralization逻辑很像但构造不同。第一，确定所需要的验证者人数方法不同。GRCACAGT是根据提议者的动态信誉值确定验证者人数，而True Decentralization是根据提议者的不诚实概率来确定验证者人数。第二，确定发起者的方法不同。True Decentralization在起始块创建时就确定了发起者。而GRCACAGT每轮共识都需要选择新的发起者，因为True Decentralization中选择发起者的方法存在发起者节点身份暴露的安全问题。分析发现，当所有验证节点身份全部暴露时，节点池中剩下的节点就是发起者节点，此时发起者的身份也会暴露。第三，发起者选择验证者的方法不同。True Decentralization是将节点池平均分为4个小的节点池，每个发起者对应一个小节点池，从对应的节点池中选择验证者。这样风险较大，因为在True Decentralization中虽然每次参与验证节点的身份在节点完成验证之后才会暴露，但经过多轮验证后，每个节点池中节点的身份都会暴露，此时通过节点出现的次数能确定哪些节点被选择的概率最大，所以少数的节点就能实现攻击。而GRCACAGT利用抽样不放回和加权随机的方法，相对True Decentralization不仅能增加4倍的安全性而且节点不会被重复选择。

在GRCACAGT中，每轮共识开始后首先随机选出发起者，并根据提议者的信誉大小确定验证者人数；然后根据更新后的信誉值加权随机选择验证者，该过程是利用抽样不放回的方法实现的，这样能够保证节点不被重复选择；最后利用博弈论分析GRCACAGT发现在验证上链阶段存在节点之间的共谋安全问题。本文将这种共谋定义为1/3节点共谋攻击，并提出共谋合约解决了该安全问题。图1为GRCACAGT模型。

1) 提议者：创建新区块并向全网广播这个块。

2) 发起者：新区块广播后确定所需要的验证者。

3) 验证者：对新提出的区块进行投票达成共识。

4) 其余节点：矿池中没有参与共识的节点。

1.1 发起者的选择

该阶段博弈在提议者（Alice）和发起者（Bob）间进行，通过博弈结果确定发起者人数。发起者有两个策略，即最小验证者（MV）和更多的验证者（AMV），AMV的大小是根据博弈结果确定的。Alice和Bob存在两种状况（诚实或不诚实），Alice不同的状况下有两种类型（作弊或不作弊）。

把4个发起者之间博弈看作一对一的独立博弈。由于Bob不知道Alice的类型，且提议者行动在先，发起者行动在后，两者的行动具有非同时性，所以该博弈是精炼贝叶斯纳什均衡（PBNE），发起者和提议者的博弈树如图2所示。

图1 GRCACAGT模型

Figure 1 GRCACAGT model

图2 发起者和提议者的博弈树

Figure 2 Game tree of initiators and proposers

表1为系统中提议者和发起者间博弈的参数说明。图3表示提议者（Alice）为不诚实节点的收益矩阵，第一个收益是Alice，第二个是Bob。图4表示提议者（Alice）为诚实节点的收益矩阵。

纯策略：假设玩家Alice知道玩家Bob的信誉值为，那么Alice确定他的策略之后，对于玩家Bob选择AMV的预期收益为

同理，玩家Bob选择MV的预期收益为

表1 参数说明

Figure 3 The utility matrix when the proposer (Alice) is the dishonest nodes

图4 提议者(Alice)为诚实节点的收益矩阵

Figure 4 The utility matrix when the proposer (Alice) is the honesty nodes

通过化简之后得到

这时对于玩家Bob来说，最好的选择是AMV。如果玩家Bob选择了AMV，那么作弊对于玩家为不诚实节点就不再是最好的决策，这时他会选择不作弊，所以((不诚实节点且作弊, 诚实节点不作弊)，选择AMV,)不是一个贝叶斯纳什均衡点。

这时玩家Bob最好的选择是MV，((不诚实节点且作弊, 诚实节点不作弊)，选择MV,)是一个纯策略的精炼贝叶斯纳什均衡。

混合策略：在式(4)成立时，不存在纳什均衡，所以存在PBNE的混合策略，假设玩家(Alice)作弊的概率为，玩家Bob选择AMV的概率为，则玩家Bob选择AMV的预期收益为

玩家Bob选择MV的预期收益为

同理，当Alice不诚实时，可预期收益函数为

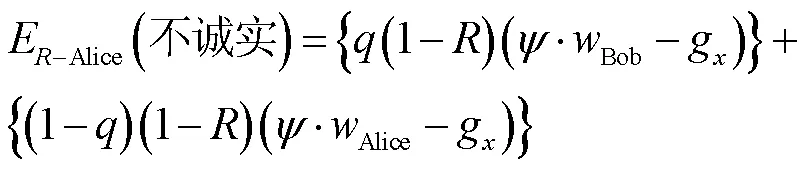
玩家不作弊的收益为

PBNE的混合策略为

这里，*是一个发起者选择AMV的概率。

PBNE混合战略的策略为

1.2 验证者的选择

1.3 节点的信誉更新

利用层次自组网中基于节点角色的新信誉模型实现动态更新[18]，可以通过将节点自身的经验与其行为和其在路由过程中的合作有效性相结合来评估信誉，通过信誉值确定节点的安全情况来选择具有较高价值的节点, 以确保通信可靠。因为不同节点之间可能存在一定的关系，可以根据节点的作用将信誉分为提议者发起者之间的信誉（PLR）、发起者验证者之间的信誉（LVR）、提议者验证者之间的信誉（PVR），根据各个信誉之间的关系制定的信誉更新模型如图5所示。

图5 信誉更新模型

Figure 5 Credibility updating model

在一轮的验证过程中，节点池中节点分为提议者、发起者、验证者和其他，每一个节点都有自己的任务，任务结束后每个节点的信誉会有所变动，通过影响信誉值元素的大小变化而更新对应节点的信誉值。随着PLR、LVR和PVR大小的变化实现节点信誉的更新。提议者提出假的交易块信誉就会被降低，区块通过验证则信誉增大。对于发起者，只有在积极参与验证的情况下信誉才会有所增加。对于验证者也是如此。

2 GRCACAGT共谋攻击

2.1 1/3节点共谋攻击

GRCACAGT在达成共识部分分为身份验证和投票达成两个阶段。首先将验证者人数平均分为两部分，一部分作为发起者身份验证阶段的验证，身份验证成功后另一部分验证者再进行投票达成共识。所以，只有身份验证和投票达成阶段结果正确共识结果才可信。通过博弈论分析发现这个过程中存在严重的安全问题。分析发现通过多次共识后，节点被选择的概率就会被暴露，概率大的节点会选择共谋，当共谋节点数量大于整体的1/3，整个区块链系统就会面临严重的安全问题。本文将这种共谋攻击称为1/3节点共谋攻击，并构建共谋合约解决了该安全问题。

对于该共谋攻击问题，本文首先分析了实现攻击的共谋节点数量及对应的概率，主要分为两个部分（最大数量的共谋节点，最小数量的共谋节点），然后利用智能合约设立共谋合约，再通过博弈论分析不同选择的效用函数证明该共谋合约的正确性。

攻击者人数越多，攻击成功的概率越大，攻击者的期望值越高，因此共谋人数通常远高于节点池中的1/3节点。

若共谋者要实现发起者身份验证结果不可信，则所有共谋节点都要在该阶段选择验证者时被选中，该概率为

通过以上分析可知在1/3节点共谋攻击中，当一些节点之间达成共谋之后, 该协议被攻击的概率是一个不能忽视的大小，因此解决1/3节点共谋攻击问题对该类算法的安全性具有重要意义。

2.2 共谋合约

2.2.1 建立合约

当矿池中的节点被选为发起者或验证者节点后，每个节点都上传一笔保证金，保证节点的诚实行为。若节点行为诚实，完成共识后将会退回，但发现节点行为不诚实时将会被扣除，在共识阶段，理性的矿工为了使自己的利益最大化会寻求共谋，对于这个共谋问题，本文利用构建共谋合约来解决。合约规定，当节点发起共谋后，接收到共谋消息的节点可以选择同意或举报，当节点选择举报策略后，发起共谋节点保证金将被扣除，而举报者获得共谋节点的保证金作为举报奖金，并且两者信誉值将会更新，合约如下。

实现共谋攻击需要矿池中多个节点共谋，矿池中每个节点之间的共谋相互独立，假设每次的共谋节点为c1和c2，节点c1和c2之间共谋，共谋合约参数如表2所示。

1) c1, c2输入时，系统自动执行()函数。

2) 节点加入区块链时支付保证金到系统，执行()函数确定是否要被扣除。

3) 举报共谋，假设c1给c2发起共谋，然后其中一方举报另一方。分为两种情况：c1给c2发起共谋，c2同意之后，c1反过来举报c2获得c2的保证金；c1给c2发起共谋，c2假装答应，等c1签字确认共谋后，c2举报c1获得c1保证金。

4) 将共谋者信誉值归零，举报者信誉增加。

表2 合约参数

2.2.2 合约分析

通过合约的建立可以得到节点c1和c2共谋双方的博弈树，如图6所示。假设c1发起共谋，c2同意的概率为1，c1举报c2的概率为2，因为在该共谋合约中作为c1不知道当它发起共谋时c2是否会同意共谋，但是可以根据共谋攻击获得的利润、获得的举报奖金以及它的信誉值等这些信息判断c2同意共谋的概率1。同样的c2会根据举报奖金、攻击成功获得的利益以及c1的一个信誉值确定被c1举报的概率2。利用不完全信息动态博弈分析该博弈，确定最后的精炼贝叶斯纳什均衡解。

图6 共谋双方的博弈树

Figure 6 Conspiracy the game tree of both parties

本文利用精炼贝叶斯纳什均衡的方法求均衡解，要达到最优必须每步最优。如图6所示。先分析c2同意共谋是否最优，对于c2来说，当它选择了同意，那么希望c1不举报它，最终达成共谋成功获得额外收益。如果2较大，那c2相对于同意的策略不是最优，即相对于c1来说选择不举报是c2选择同意的目的，即

化简之后为

由

则有

因此，c1会大概率举报c2，而对于c2来说，同意共谋就不再是当前最优策略，因此c2会举报c1，而这时对于c1来说，发起共谋也不是最优策略。

每个节点最终都是为了自己的利益最大化，当一个节点发起共谋时，根据博弈树中的线路必定最后会被另一方举报，这时双方就会形成囚徒困境。它的效用函数为

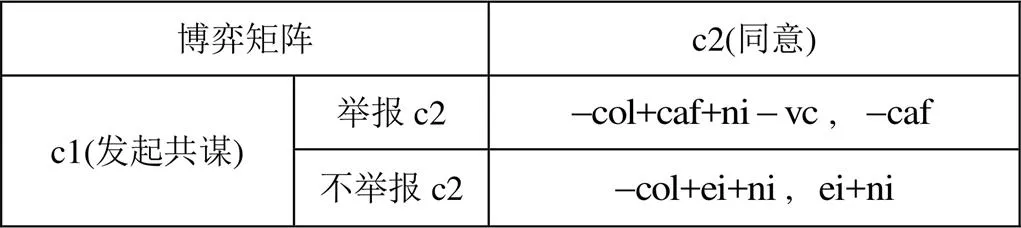
图7 c1发起共谋后c2同意的效用函数

Figure 7 The utility function c2 agrees to after c1 initiates a conspiracy

图8 c1发起共谋后c2不同意的效用函数

Figure 8 The utility function that c2 disagrees with after c1 initiates a conspiracy

图9 c1和c2不共谋的效用函数

Figure 9 c1 and c2 are not collusive utility functions

3 安全性分析

3.1 抗DDoS和Eclipse attacks攻击

在GRCACAGT共识算法中，矿池中节点分为提议者、发起者、验证者和其他，其中发起者和验证者身份的匿名保证了共识算法的安全性，如果发起者和验证者身份暴露，则很可能发生DDoS攻击和Eclipse attacks攻击[19]，这两种攻击都需要事先知道验证发起者和验证者，提出的共识协议中，用智能合约和加权随机函数实现发起者和验证者的随机化，并保证节点之间的身份匿名，从而防止DDoS攻击和Eclipse attacks攻击。

3.2 抗1/3节点共谋攻击

利用博弈论分析容错类的共识算法中得到，该类共识算法每轮投票都需要保证正确节点多于错误节点的3倍，当大于1/3节点发生共谋则最终达成的共识结果不可信。对于该问题，在GRCACAGT共识算法中利用智能合约和博弈论方法设计了共谋合约，当有节点发起共谋时，理性地接收节点最终会选择举报共谋而获得收益，而对于共谋发起者来说这种策略是对其损失最大的策略，因此对于矿池中理性的矿工节点不会选择发起共谋，从而防止了1/3节点共谋攻击。

3.3 信誉动态更新增强共识算法的正确性

一个人的信誉是变化的，并且一个人的不诚实概率等于信誉的对立。因此，本文利用构建的信誉模型对节点信誉进行更新，利用提议者的信誉值代替提议者的不诚实概率能够使本文的共识算法更加高效，同时验证者的数量更加准确，提高共识算法正确性。

4 实验分析

容错类共识算法中共谋攻击的概率是不可以忽略的。本文对基于拜占庭容错的共识算法进行7次共识实验，分别进行20次、50次、80次、110次、140次、170次、200次共识过程。

在假设所有节点被选择的概率相等下得到最后1/3节点共谋攻击成功的次数和每次共谋成功的概率为0.436 4，如图10所示。

图10 1/3节点共谋攻击情况分析

Figure 10 Analysis of conspiracy attack of 1/3 nodes

实际情况是，节点为了更大概率地实现攻击会选择概率大的节点进行共谋，因此实现共谋攻击的概率大于0.436 4。本文通过建立共谋合约制止节点之间的这种共谋。

发起者开销为

验证者确认的时间开销为

投票者确认阶段时间开销

总的时间开销为

通过对比PoW、PoS、True Decentralization和GRCACAGT性能指标（如表3所示），发现GRCACAGT相对PoW和PoS在TPS、时延、交易确认时间、交易不可更改时间、资源消耗方面具有优势，相对True Decentralization具有更高的安全性。

表3 PoW, PoS, True Decentralization, GRCACAGT性能指标

吞吐量是衡量系统单位时间内处理交易的能力。本文使用每秒交易数（TPS，transaction per second）来表示吞吐量，比较了True Decentralization和GRCACAGT两种共识机制的吞吐量，区块链网络中吞吐量指单位时间内交易从产生到被确认并写入区块链中的交易总数，计算如下：

图11 True Decentralization和GRCACAGT吞吐量比较

Figure 11 Comparison of throughput with True Decentralization and GRCACAGT

运行两个共识协议30次后对比两者的运行时间，True Decentralization和GRCACAGT一轮验证时间对比如图12所示。

图12 True Decentralization和GRCACAGT运行时间对比

Figure 12 Run time comparison of True Decentralization and GRCACAGT

通过图12能够清楚地知道，GRCACAGT 在时间上相比True Decentralization更有优势。

5 结束语

本文利用博弈论、映射函数和加权随机函数，提出了GRCACAGT。GRCACAGT主要解决容错类算法中节点的全局随机化问题，并利用博弈论分析发现这类算法中存在共谋攻击，然后构建共谋合约解决这类共谋攻击从而实现该类算法的高安全性。安全性分析表明，GRCACAGT抗DDoS、Eclipse attacks、不诚实节点贿赂和与1/3节点共谋等攻击。实验分析对比了GRCACAGT和相似的一些共识算法的吐量、交易完成时间、时间开销等性能。实验结果表明，GRCACAGT在安全性和效率性方面得到了很大的提高。本文在选择验证节点时通过不放回抽样的方法避免节点被重复选中，但是该方法使协议的效率变低。并且，在信誉的动态更新模型中，本文没有具体设置模型的参数，对于影响信誉大小的元素没有具体构造出来。因此，高效地实现节点不被重复选择和信誉更新模型具体的构建是下一步工作的方向。

[1] TILBORGH C A, JAJIDIA S. Encyclopedia of cryptography and security[M]. US：Springer, 2011.

[2] GANESH C, ORLANDI C, TSCHUDI D. Proof-of-stake protocols for privacy-aware blockchains[C]//Advances in Cryptology – EUROCRYPT 2019, 2019

[3] KIAYIAS A, RUSSELL A, DAVID B, et al. Ouroboros: a provably secure proof-of-stake blockchain protocol[C]//Advances in Cryptology – CRYPTO 2017.

[4] KERBER T, KIAYIAS A, KOHLWEISS M, et al. Ouroboros crypsinous: privacy-preserving proof-of-stake[C]//Proceedings of 2019 IEEE Symposium on Security and Privacy. 2019: 157-174.

[5] FAN X X, CHAI Q. Roll-DPoS: a randomized delegated proof of stake scheme for scalable blockchain-based Internet of things systems[C]//Proceedings of the 15th EAI International Conference on Mobile and Ubiquitous Systems: Computing, Networking and Services. 2018.

[6] BUCHMAN E, KWON J, MILOSEVIC Z. The latest gossip on BFT consensus[EB].

[7] ALZAHRANI N, BULUSU N. Towards true decentralization: a blockchain consensus protocol based on game theory and randomness[C]//Decision and Game Theory for Security, 2018.

[8] BENTOV I, LEE C, MIZRAHI A, et al. Proof of activity[J]. ACM SIGMETRICS Performance Evaluation Review, 2014, 42(3): 34-37.

[9] CHEPURNOY A. Interactive proof-of-stake[EB].

[10] SABZMAKAN A, MIRTAHERI S L. An improved distributed access control model in cloud computing by blockchain[C]//Proceedings of 2021 26th International Computer Conference, Computer Society of Iran (CSICC). 2016: 1-4.

[11] GILAD Y, HEMO R, MICALI S, et al. Algorand: scaling Byzantine agreements for cryptocurrencies[C]//Proceedings of the 26th Symposium on Operating Systems Principles. 2017.

[12] OMAR M, CHALLAL Y, BOUABDALLAH A. Reliable and fully distributed trust model for mobile ad hoc networks[J]. Computers & Security, 2009, 28(3/4): 199-214.

[13] ZHAN Y, WANG B C, LU R X, et al. DRBFT: Delegated randomization Byzantine fault tolerance consensus protocol for blockchains[J]. Information Sciences, 2021, 559: 8-21.

[14] DONG C Y, WANG Y L, ALDWEESH A, et al. Betrayal, distrust, and rationality: smart counter-collusion contracts for verifiable cloud computing[EB].

[15] CHEN H, LAINE K, PLAYER R. Simple encrypted arithmetic library - SEAL v2.1[M]. Berlin:Springer, 2016.

[16] ANDERW M, YU X, KUYLE C,et alThe Honey badger of BFT Protocols[R]. 2016.

[17] JALALZAI M, BUSCH C, JII G R. Proteus: a scalable bft consesus protocol for blockchains[C]//CORR .2019.

[18] LESSMANN S, BAESENS B, SEOW H V, et al. Benchmarking state-of-the-art classification algorithms for credit scoring: an update of research[J]. European Journal of Operational Research, 2015, 247(1): 124-136.

[19] 王缵, 田有亮, 岳朝跃, 等. 基于门限密码方案的共识机制[J]. 计算机研究与发展, 2019, 56(12): 2671-2683.

WANG Z, TIAN Y L, YUE C Y, et al. Consensus mechanism based on threshold cryptography scheme[J]. Journal of Computer Research and Development, 2019, 56(12): 2671-2683.

[20] YU Y L, CHEN T S. An efficient threshold group signature scheme[J]. Applied Mathematics and Computation, 2005, 167(1): 362-371.

Global randomized consensus algorithm resist collusion attack based on game theory

ZHANG Bao1,2, TIAN Youliang1,2, GAO Sheng3

1. Computer Science and Technology Institute, Guizhou University, Guiyang 550025, China 2. Guizhou Provincial Key Laboratory of Public Big Data, Guiyang 550025, China 3. Information Institute CentralUniversityofFinanceandEconomics, Beijing 100081, China

As the cornerstone of blockchain technology, consensus technology has received more attention with the continuous development of blockchain technology. The development of consensus technology has become more and more rapid, but there are still related problems. Nowadays, fault-tolerant consensus algorithms, as one of the representative blockchain consensus technologies, still have many problems to be studied. The problem of node randomness and node collusion attacks in fault-tolerant consensus algorithms had been studied, and a game-theoretic-based anti-corruption algorithm was proposed. The global randomization consensus algorithm of collusion attack improved the security and throughput of the blockchain network by realizing the randomization of nodes and solving related security problems. In the process of selecting nodes participating in the fault-tolerant consensus algorithm, the global randomization of the initiator and verifier nodes was realized by using the mapping function and the weighted random function, thereby ensuring the identity anonymity of the initiator and verifier nodes and improving the blockchain network security accordingly. The reputation update model was used to realize the dynamic update of the reputation, and the game theory was used to analyze the security problems of the fault-tolerant consensus algorithm. A more correct and efficient algorithm model was constructed to improve the throughput of the algorithm and analyze the problem of collusion attack of more than one third of the nodes in this kind of algorithm, the refined Bayesian game was used to construct a collusion contract and analyze the collusion The Nash equilibrium point between the two nodes was adopted to solve the collusion attack problem of more than one third of the nodes. The security analysis and experiments show that the global randomization consensus algorithm based on the game theory anti-collusion attack is better than PoW、PoS and PBFT. The consensus algorithm is not only effective to improve throughput and reduce computing resource consumption, but also resistant to DDoS, Eclipse attacks and collusion attacks by more than one third of nodes.

consensus algorithm, global randomization, game theory, conspiracy attack

The National Natural Science Foundation of China (61662009, 61772008), Science and Technology Major Support Program of Guizhou Province (20183001), Key Program of the National Natural Science Union Foundation of China (U1836205), Science and Technology Program of Guizhou Province ([2019]1098), Project of High-level Innovative Talents of Guizhou Province ([2020]6008), Science and Technology Program of Guiyang ([2021]1-5)

张宝, 田有亮, 高胜. 基于博弈论抗共谋攻击的全局随机化共识算法[J]. 网络与信息安全学报, 2022, 8(4):98-109.

TP393

A

10.11959/j.issn.2096−109x.2022048

张宝（1995−），男，贵州毕节人，贵州大学硕士生，主要研究方向为密码学、区块链网络和共识算法。

田有亮（1982−），男，贵州盘州人，博士，贵州大学教授、博士生导师，主要研究方向为算法博弈论、密码学与安全协议、大数据安全与隐私保护、区块链与电子货币等。

高胜（1987−），男，湖北黄冈人，博士，中央财经大学副教授，主要研究方向为数据安全与隐私保护、区块链技术及应用。

2021−11−22；

2022−03−01

田有亮，youliangtian@163.com

国家自然科学基金（61662009，61772008）；贵州省科技重大专项计划（20183001）；国家自然科学基金联合基金重点支持项目（U1836205）；贵州省科技计划项目（[2019]1098）；贵州省高层次创新型人才项目（[2020]6008）；贵阳市科技计划项目（[2021]1-5）

ZHANG B, TIAN Y L, GAO S. Global randomized consensus algorithm resist collusion attack based on game theory[J]. Chinese Journal of Network and Information Security, 2022, 8(4): 98-109.