基于荧光发射光谱的水质化学需氧量检测研究

胡钢强

(山东省调水工程运行维护中心棘洪滩水库管理站，山东 青岛 266000)

化学需氧量(COD)常用于表示水体内的污染物参数，其数值越大，代表水质较差，受污染较严重。在目前节能减排、绿色发展的大环境下，化学需氧量的检测技术已成为学者专家的研究热点。

周昆鹏等人[1]提出一种检测化学需氧量的方法，建立数学模型对光谱数据进行预测，并研究不同激光波长对预测结果的影响。王晓明等人[2]基于极限学习机算法，建立数学预测模型，以检测水体中的COD含量。曹煊等人[3]设计了一种海水化学需氧量分析系统，分析水体中各种因素变化对化学需氧量含量的影响。买巍等人[4]基于多元分析法，并采用两种算法，对染料溶液中的化学需氧量进行检测。马睿等人[5]建立化学需氧量去除模型，研究某污水厂的化学需氧量去除效率。

本研究基于偏最小二乘回归法和主成分回归法，建立数学模型，对水体的COD浓度进行预测，对比其预测效果的准确性，并将其与实际值对比，验证预测模型的合理性。同时也对水样采样属地棘洪滩水库水质化学需氧量监测情况起重要作用。

1 实验部分

本实验采取含有COD的溶液与不含COD的标准水样作为研究对象，对其进行对比实验。标准水样取自青岛棘洪滩水库水，将其在自然条件下进行静置后，取其上层水样，作为研究对象。含有COD的溶液浓度最小值为2.5mg·L-1，浓度最大值为100mg·L-1。

1.1 实验地的基本资料

实验标准水样取自山东省青岛市棘洪滩水库，棘洪滩水库库区面积14.42km2，围坝长14.227km，总库容约1.46亿m3，由围坝、棘洪滩泵站、输水河、进水闸、放水洞、泄水洞、桃源河改道等工程组成。棘洪滩水库是青岛市最重要的供水水源地，水库的水质状况和水质安全受到社会各界的关注[6]该水库水质多年来一直满足地表水Ⅲ类水标准，棘洪滩水库作为一座调蓄型平原水库，引水水质的好坏直接影响库内水体的质量，主要污染项目为总磷、高锰酸盐指数和五日生化需氧量。

本研究对实验用水的化学需氧量进行测量及分析，采用的实验仪器为荧光分光光度计。标准水样采取消解器和分光光度计进行测定其相关离子含量[7- 8]。

在实验过程中，水样中的物质会与电磁波相互作用，进而产生散射峰。散射峰会影响实验过程的数据准确性，在进行实验之前，需要对实验用水中的散射峰进行去除。在去除实验水体的散射峰后，分析实验水体的荧光光谱图可得，当激发波长为270mm时，荧光发射光谱的增量最大。因此，将270mm作为最优激发波长，340mm作为最优发射波长，以此作为基准值，得出在最优激发波长和最优发射波长下的光谱数据。以此光谱数据作为基准值，建立相关数学模型，对实验用水的化学需氧量进行分析。采用快速消解分光光度法，对实验水样的化学需氧量理论值进行测量，对其测量结果取平均值，以保证实验结果的精度。经过实验测定的实验用水的化学需氧量浓度为0.64～44.5mg·L-1。

1.2 数学模型的建立与验证

将上述实验测得的实验用水的化学需氧量浓度通过数学模型进行分析，采用偏最小二乘回归法(PLSR)和主成分回归法(PCR)进行计算分析。为保证数学模型分析结果与试验结果的一致性，需要对实验用水进行相应的处理：在含有COD的溶液中抽取15组作为数学建模分析对象，在不含COD的标准水样中抽取48组作为数学建模分析对象，将其余实验用水作为检验集，根据检验集的结果对数学模型的计算结果进行对比分析，以验证其精度。

2 结果与讨论

2.1 COD溶液光谱模型的建立

采用偏最小二乘回归法和主成分回归法对实验数据进行建模分析。当主成分回归法主成分分数取8，偏最小二乘回归法主成分分数取5时，数学模型的计算结果较好，所以取上述主成分分数，对实验数据进行建模。偏最小二乘回归法和主成分回归法的建模结果如图1所示。

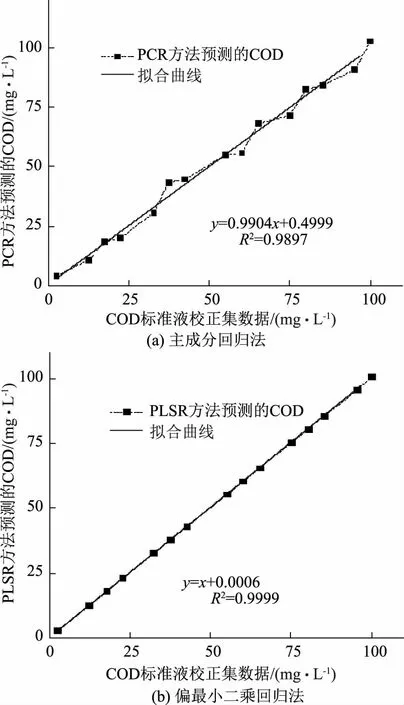
图1 COD溶液数学模型建模结果

最小二乘回归法和主成分回归法预测值与检验集理化值对比见表1。

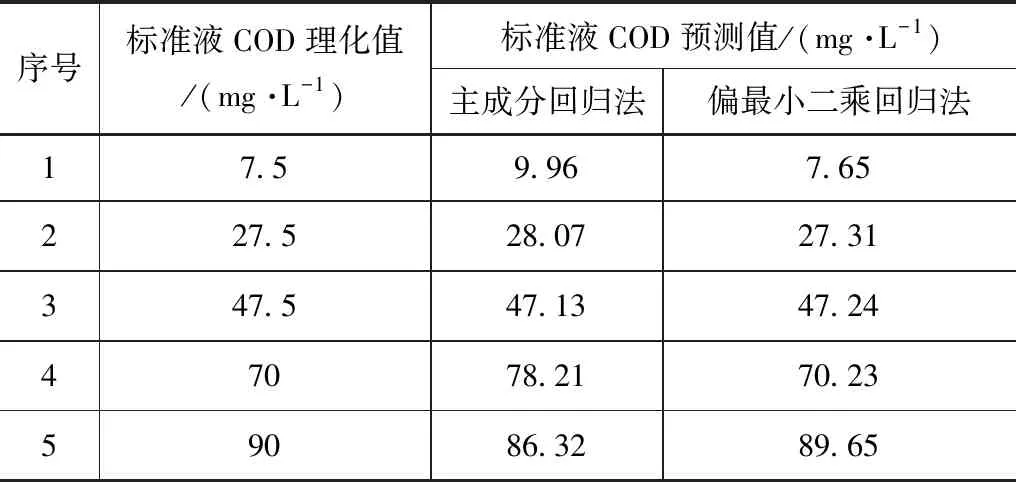
表1 COD标准液的预测值对比

由图可知，主成分回归法和最小二乘回归法拟合曲线的相关系数分别为0.9897、0.9999，相关性良好。采用最小二乘回归法建立的数学模型得出的结果与COD标准液校正集数据对应情况良好，且其拟合曲线的相关系数大于主成分回归法，所以采用最小二乘回归法数学模型分析COD荧光发射光谱数据比主成分回归法准确性更高。

由表1可得，采用主成分回归法分析标准液COD预测值与标准液COD理化值差距较大，最大差距为序号1的COD预测值，差距为32%，最小差距为序号3的COD预测值，差距为0.7%。采用偏最小二乘回归法分析标准液COD预测值与标准液COD理化值差距较小，最大差距为序号1的COD预测值，差距为2%，最小差距为序号4的COD预测值，差距为0.32%。通过对比标准液的COD理化值与预测值可得，采用偏最小二乘回归法对COD浓度进行预测准确度较高，最大误差不超过2%，且预测效果较为稳定，采用主成分回归法进行预测的准确度不稳定，最大误差为32%，最小误差为0.7%，预测效果不稳定，且预测精度不高。这是由于，在试验过程中，存在一些难以避免的误差，配置COD溶液时会产生误差，实验用具的清洁程度也会使结果产生误差。

2.2 实际水样光谱模型的建立

由于实际水样直接取自于棘洪滩水库，在进行试验前只将其进行静置处理，对其进行光谱分析时，其干扰因素较多，所以需要对其数据进行处理后，再进行数学模型建模。基于最小二乘原理，使用多项式算法对数据进行处理。探究试验水样的主成分分数、隐含变量和预测残差平方和(PRESS)之间的关系，如图2所示。

由图可知，当使用偏最小二乘回归法时，当主成分数为6时，有最小残差平方和；当使用主成分回归法时，当主成分数为7时，有最小残差平方和。残差平方和可表示数学模型的预测能力，当其数值越小时，代表其预测准确度越高。综上所述，选用主成分数为6和7作为基准值，对实验用水的COD含量进行预测，在此基础上，对其预测模型进行校正，如图3所示。

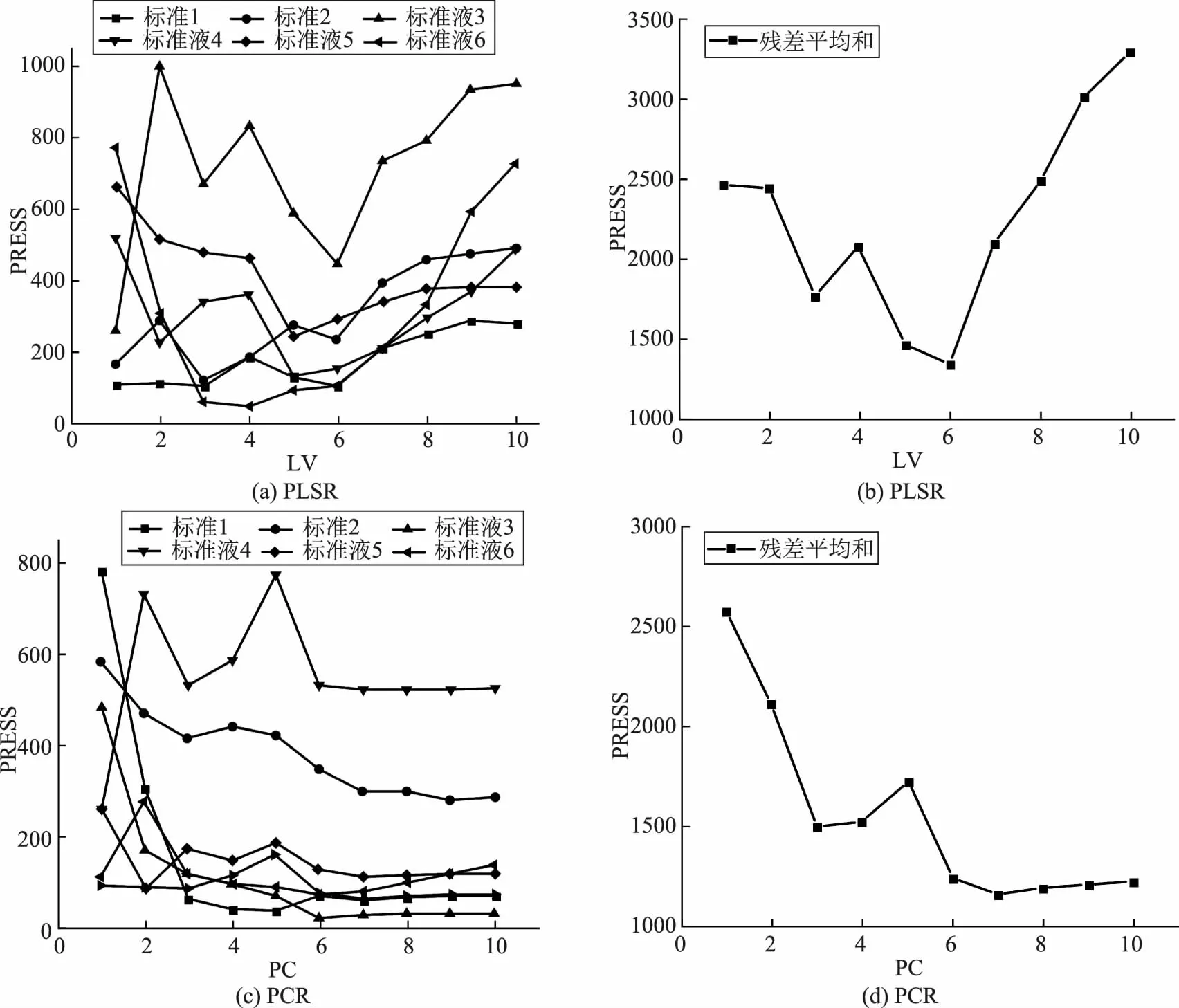
图2 残差平方和与主成分数、隐含变量的关系

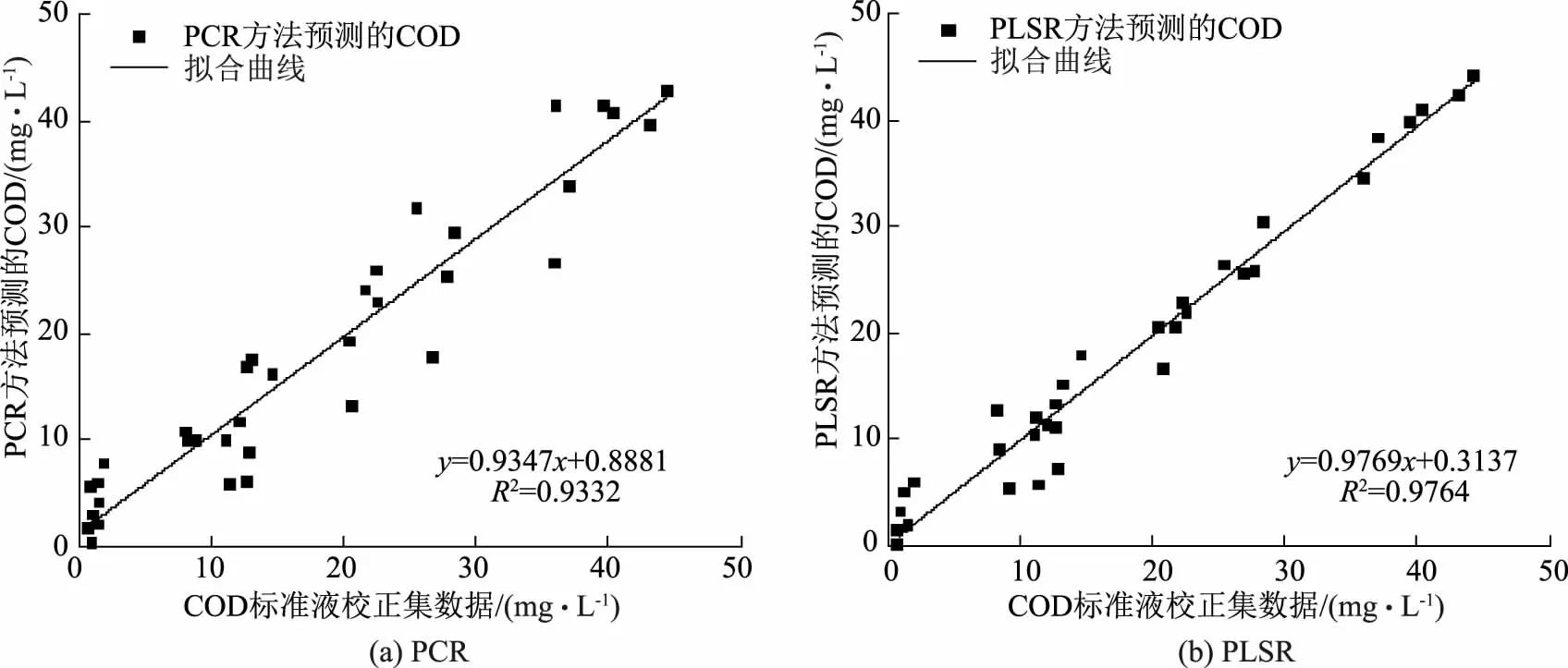
图3 实际水样光谱数据模拟结果对比

由图可知，利用主成分回归法拟合曲线的相关系数为0.9332，利用偏最小二乘回归法的拟合曲线的相关系数为0.9764，说明两种方法拟合的相关性良好。由于偏最小二乘回归法的相关系数大于主成分回归法，所以其预测值更加准确。预测值的大部分值集中于拟合曲线旁，但是存在少量点离拟合曲线较远，这是由于在试验过程中，会产生难以避免的误差，导致试验结果与实际值之间存在误差，影响预测的准确性。将检验集的数据利用偏最小二乘回归法和主成分回归法进行分析，如表2所示。由表可知，两种方法分析标准液COD预测值与标准液COD理化值准确度不稳定，采用偏最小二乘回归法最大差距为序号11的COD预测值,,采用主成分回归法最大差距为序号11的COD预测值。总体而言，通过对比标准液的COD理化值与预测值可得，采用偏最小二乘回归法对COD浓度进行预测准确度较高，且预测效采用主成分回归法进行预测的准确度不稳定，且预测精度不高。

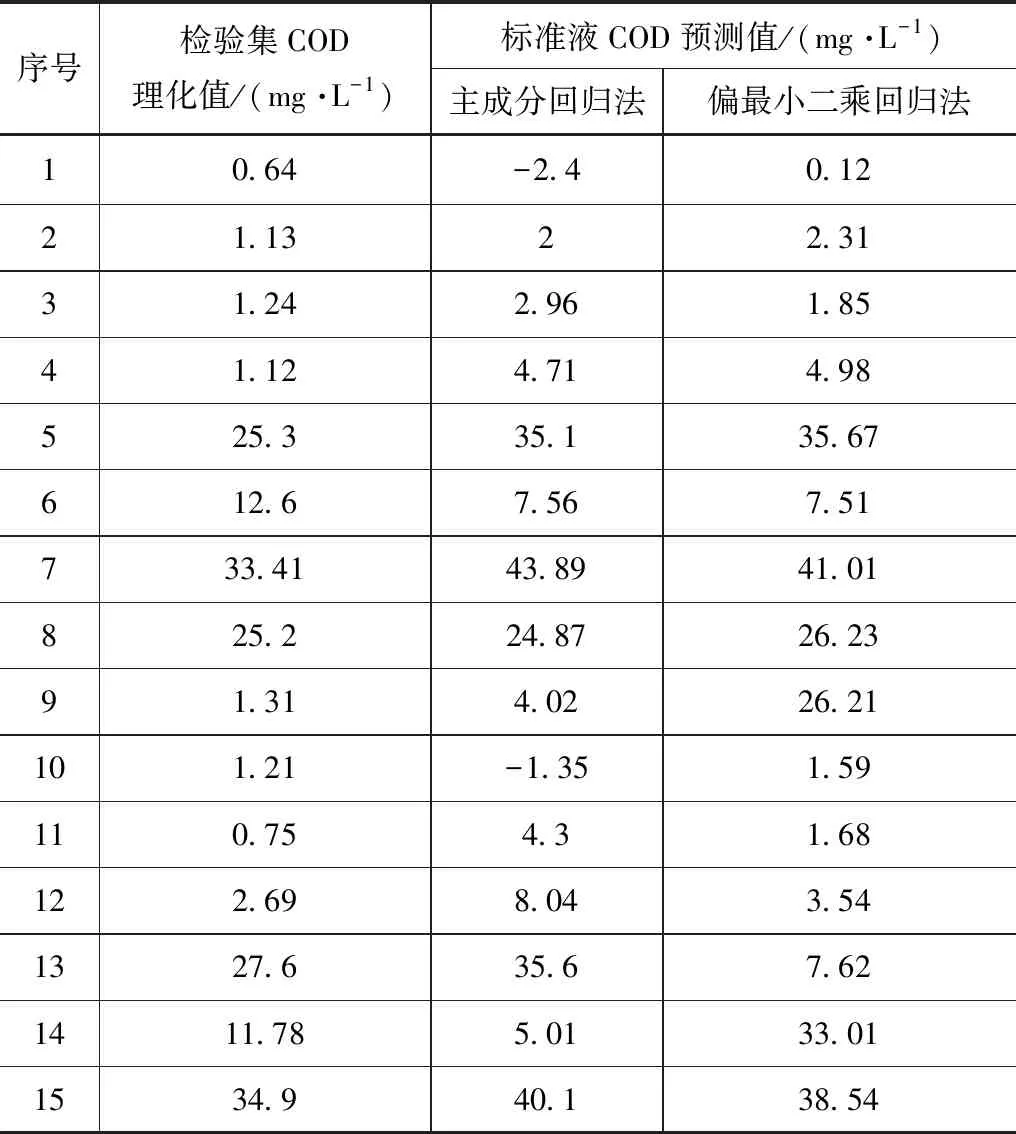
表2 实际水样检验集COD预测结果

图4为实际水样检验集预测值。由图可知，采用主成分回归法拟合曲线的相关系数为0.919，利用偏最小二乘回归法的拟合曲线的相关系数为0.9402，说明两种方法拟合的相关性良好。由于偏最小二乘回归法的相关系数大于主成分回归法，所以其预测值更加准确。

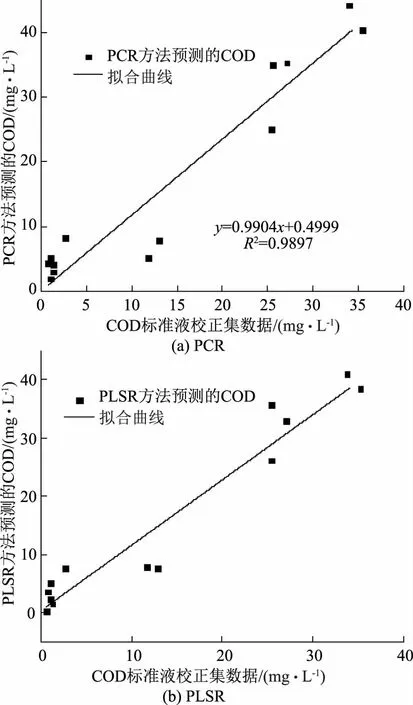
图4 实际水样检验集预测

2.3 本方法与传统方法对比

为验证本方法建立的数学模型(PLSR)的准确性，采用相同条件下的试验用水，在试验室对其COD浓度进行检测，结果见表3。

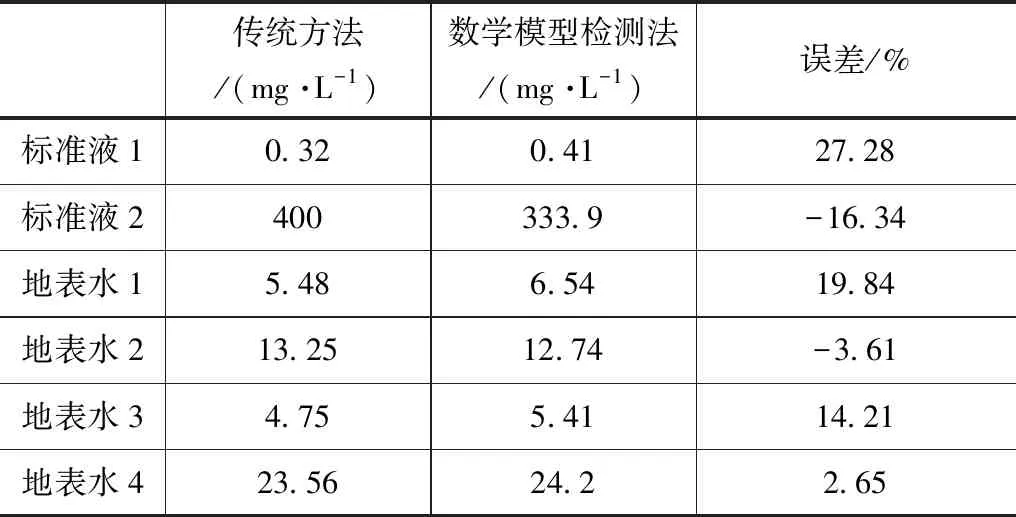
表3

由表可得，采用偏最小二乘回归法预测地表水的COD浓度误差较小，而对于标准液而言，其误差较大。这是由于，标准液为实验室配置的，而地表水含有其他物质，物质成分复杂，其预测情况与实际水样的变化规律相似，水样采用偏最小二乘回归法预测地表水的COD浓度误差较小。综上所述，采用偏最小二乘回归法对水体的COD含量进行预测，其准确度较高。

3 结语

(1)采用最小二乘回归法建立的数学模型得出的结果与COD标准液校正集数据对应情况良好，且其拟合曲线的相关系数大于主成分回归法；采用主成分回归法分析标准液COD预测值与标准液COD理化值差距较大，采用偏最小二乘回归法分析标准液COD预测值与标准液COD理化值差距较小，预测效果较稳定。

(2)采用偏最小二乘回归法预测地表水的COD浓度误差较小，而对于标准液而言，其误差较大。采用偏最小二乘回归法对水体的COD含量进行预测，其准确度较高。基于荧光发射光谱的水质化学需氧量检测方法对于了解棘洪滩水库化学需氧量水质状态的基本现状，提高水质安全管理水平，保障水源地水质。