压力特性曲线法在输气管道堵塞定位中的应用

黄港港，周阳

西安石油大学 石油工程学院（陕西 西安 710065)

0 引言

管道输送是天然气的主要输送方式。为满足国民对于天然气的旺盛需求，我国天然气管道总里程逐年增加。截至2020年底，已建成8.6×104km天然气长输管道[1]。气体杂质沉积、腐蚀产物聚集、水合物生成等均可导致管道堵塞。堵塞事故发生后，管道流量、输送效率等均不断降低，严重时可导致整个管道系统功能失效[2-3]。堵塞物质的积累是一个渐进的过程，管道堵塞初期即不完全堵塞阶段，管内压力、流量变化不大，难以监测，一旦形成完全堵塞，管道立即停输。因此，开展管道不完全堵塞定位技术研究，对于保障管道系统稳定运行具有重要意义[4]。

目前，输气管道堵塞定位技术主要有应力应变法、透射检测法、压力体积法、压力波法等[5-6]。但这些方法均存在一定的局限性。应力应变法和透射检测法需要开挖管道后使用专业设备进行检测，实施困难；压力体积法检测周期长且成本较高；近几年，关于压力波法的研究较多，但在不完全堵塞定位问题上，压力波法仍具有一定局限性[7-8]。压力特性曲线法无需借助其他设备，仅从管道运行数据即可实现不完全堵塞定位，具有易操作、效率高、成本低等优势[9]。但目前国内关于输气管道压力特性曲线的研究与应用较少。为提高堵塞定位效率，保障管道安全运行，对压力特性曲线法在输气管道堵塞定位问题中的适用性进行相关研究。

1 管道不完全堵塞工况分析

如图1 所示，输气管道堵塞初期阶段堵塞点前由于管道憋压，起点压力不断上升；堵塞点处气体由于节流效应压力突降；由于堵塞点处气体产生额外的能量损失，管道终点处压力不断降低，管道流量持续降低；一段时间后，管道起终点压力、流量再次达到稳定状态，但已偏离正常工况[10]。此时，管道起终点压差由ΔP1增加至ΔP2。通过设置ΔP变化阈值，可判断管道不完全堵塞工况是否发生[11]。

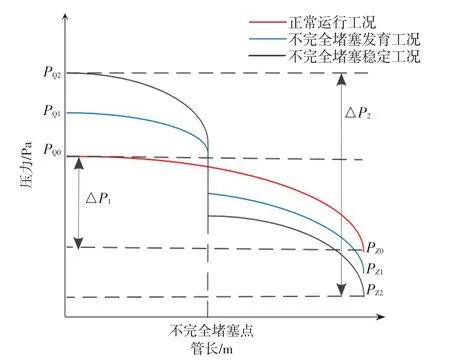
图1 输气管道不完全堵塞沿程压力分布

2 堵塞定位原理及技术路线

2.1 压力特性曲线法堵塞定位原理

如图2所示，不完全堵塞稳定工况下，管道沿程压力、流量、管存量均不随时间变化。迅速关闭起、终点阀门，进行关阀测试。由于堵塞点前后管段连通，管道沿程压力会自动平衡并达到稳定值Pbalance。压力稳定后，管道各点压力均为Pbalance。使用Pbalance计算所得的管存量记为实际管存Vc，使用沿程压力分布曲线积分所得的管存量记为理论管存V，两者满足Vc=V[9]，此为压力特性曲线法核心思想。

图2 输气管道不完全堵塞起终点压力变化趋势

为简化计算过程作出以下假设：①输气管道为一维、水平、等温管道；②气体压缩系数和管道摩阻系数为定值；③不完全堵塞段长度与管道总长度相比极短且唯一。堵塞点前后输气管道均为正常管道，使用参数PQ2、PZ2、流量Q2，结合式（1）即可计算沿程压力分布曲线[12]。其中，PQ2、PZ2分别为堵塞稳定工况下管道起点、终点压力，Pa；Q2为堵塞稳定工况下的管道流量，m3/s。

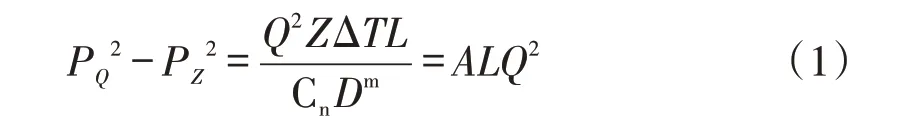
式中：Q为管道体积流量，m3/s；Cn为常数；Dm为管道内径，m；Z为气体压缩因子；Δ为气体相对密度；T为管道运行温度，K；L为管道长度，m；PQ为管道起点压力，Pa；PZ为管道终点压力，Pa；在简化条件下A为常数。

堵塞点处压力突降会使管道实际沿程压力分布如图3 中曲线PQ2-A-C-PZ2或PQ2-B-D-PZ2所示。关阀测试后，实际管存Vc可表示为Pbalance与坐标轴围成的矩形面积，并由式（2）计算[13]。

式中：Vgd为管道容积，m3；P0为标况压力，101 325 Pa；T0为工程标况温度，293.15 K；Z0为工程标况下空气压缩因子；Z为实际气体压缩因子。

理论管存V由压力分布曲线对管长积分所得，且积分值与不完全堵塞点位置相关。由图3 可知，不完全堵塞点1、2 处对应积分差值为阴影部分面积，且随两点间距增加积分差值阴影部分面积不断增大。由此可知，不完全堵塞点位置越靠近终点积分值越大，即管道存气量是堵塞位置的单调函数。以不完全堵塞点位置为自变量，建立管存函数模型，使用优化算法即可反算事故点具体位置。

图3 压力特性曲线法示意图

2.2 技术路线

由上述分析可知，不完全堵塞定位过程可等价于参数优化问题。待优化变量为不完全堵塞点位置，优化目标函数为压力分布曲线积分面积V(l)，目标函数最优值为关阀测试后实际管道存气量Vc，见式（3）。其中a为气体体积转换系数。

此为一元函数参数最优化问题，可通过优化算法求解。粒子群优化算法(PSO)原理简单、计算速度快、适应性强，广泛用于求解优化问题。选用PSO算法进行后续分析，PSO算法原理为：对于N个自变量的优化问题，首先在搜索空间内产生M个粒子，计算每个粒子适应度，然后每个粒子根据自身适应度最优值Pbest和全局适应度最优解Gbest更新自身速度和运动方向，从而不断寻找最优值[4]。粒子速度、位置更新关系式如下。

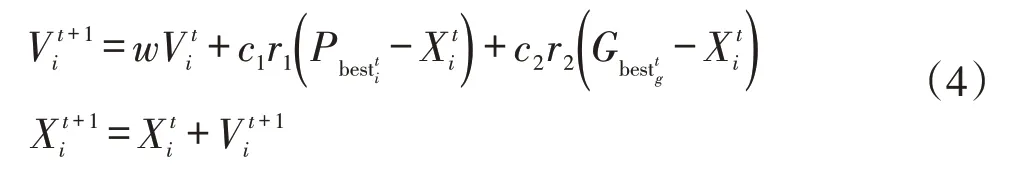
式中：Vti、Xti分别为第i个粒子在t时刻的搜索速度和空间位置；c1、c2分别为粒子对自身适应度最优值和整体适应度最优值的学习因子；w为粒子自身的惯性权重；r1、r2为随机数。

不完全堵塞定位技术路线如图4所示。

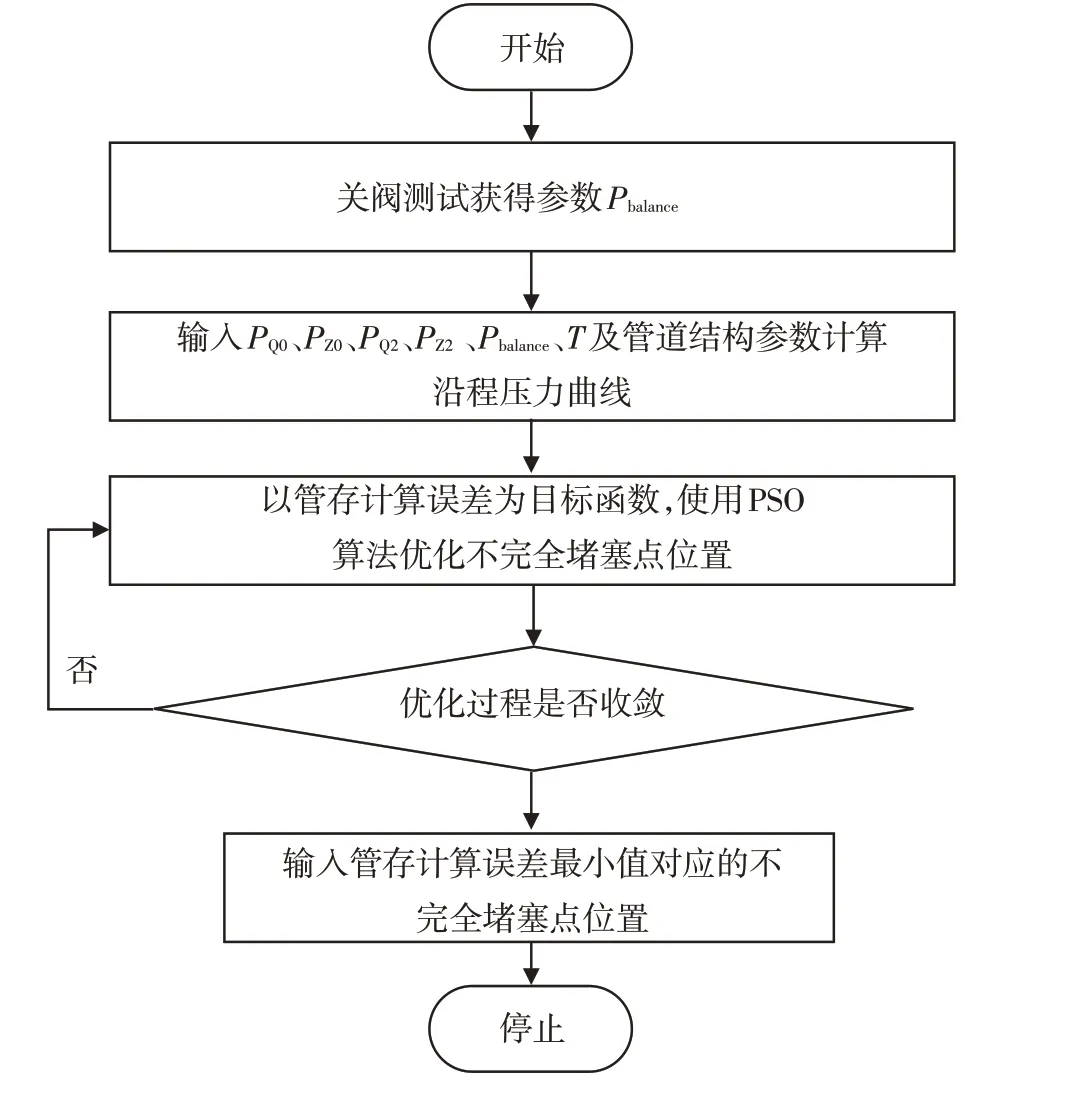
图4 不完全堵塞定位技术路线

3 实验研究

研究过程中，首先基于Matlab 建立输气管道理论沿程压力分布曲线计算模型；然后对管道参数系统进行校正；最后通过PSO 算法对不完全堵塞位置进行求解。同时，采用遗传算法(GA)以及模拟退火算法(SAA)进行对比计算，分析不同优化算法在不完全堵塞定位问题中的适用性。

3.1 实验设备介绍及实验设计

设备参数型号及相关参数见表1，设备流程图如图5所示，空气经压缩机加压后，由气水过滤器去除水分，最后进入PU管道。管道95 m和190 m处设置节流阀，实验过程中可通过调节节流阀开度模拟多个不完全堵塞工况。起终点压力、流量数据由PLC设备实时采集。

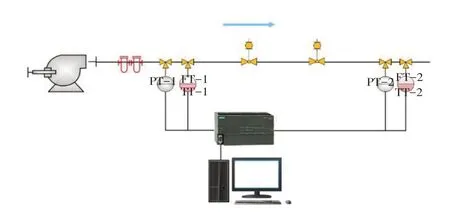
图5 实验设备流程图

表1 实验设备型号及参数

实验过程中，首先全开两节节流阀进行正常工况测试，获得管道正常运行参数PQ0、PZ0并检查装置气密性，之后分别调节两节节流阀开度，进行不完全堵塞工况模拟，运行参数稳定后由PLC设备读取PQ2、PZ2、流量Q2，关阀测试后读取管道平衡压力Pbalance。由于实验设备能力有限，共进行11 次实验，包括：1次管道正常运行工况模拟；10次不完全堵塞工况模拟。相关实验数据见表2。

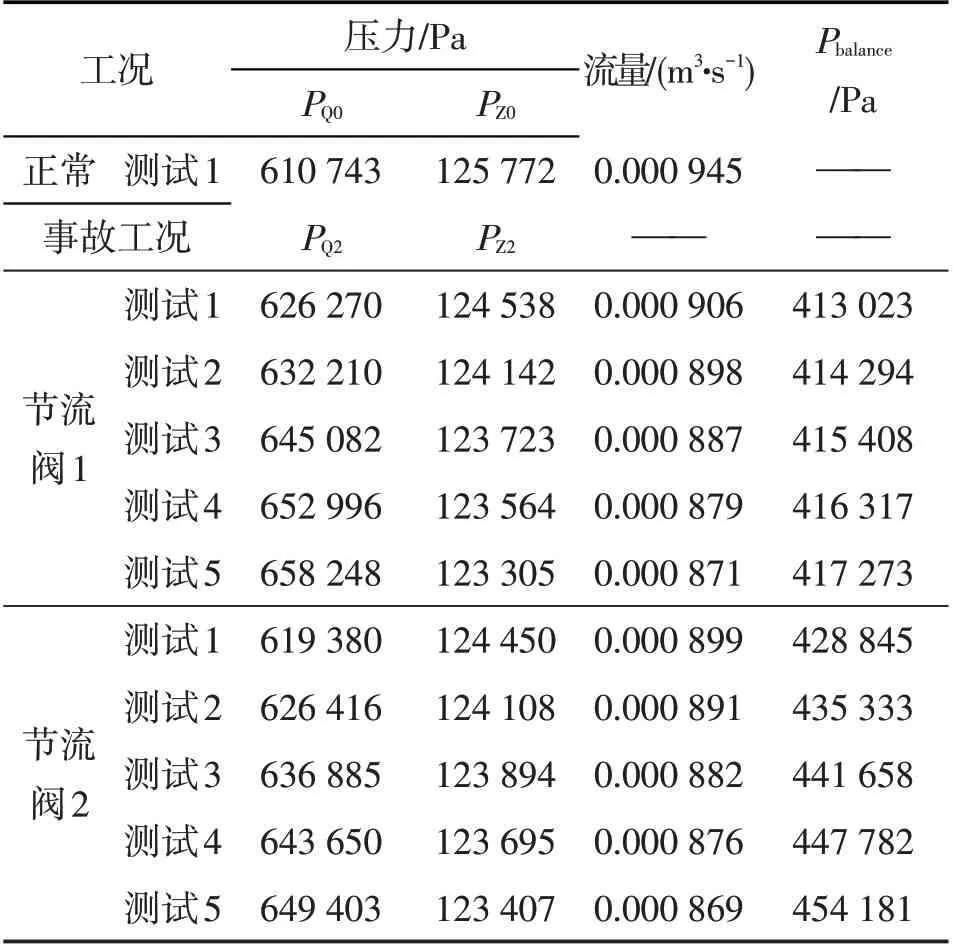
表2 室内实验数据汇总

3.2 不完全堵塞定位计算结果分析

分别使用PSO、GA、SAA 对上述10 组事故工况进行堵塞定位，计算结果如图6所示。

由图6 可以看出，压力特性曲线法可应用于输气管道不完全堵塞问题，将定位问题转化为最优化问题后，结合现代优化算法定位效果良好。从两个节流阀的定位结果看，PSO 算法定位效果优于GA、SAA 算法，定位结果与节流阀实际位置更为接近；对于全长288 m 实验管道，PSO 算法对于两节流阀定位误差为1.4～3.1 m，定位精度最高；从计算时长看，PSO算法整体低于2 s，定位速度最快。

图6 PSO、GA、SAA算法定位结果

尽管如此，采用压力特性曲线与优化算法结合的方式定位管道不完全堵塞位置仍存在一定误差，误差来源包括：①空气湿度较高，气水过滤器过滤能力有限，水分的存在导致起终点压力表和流量表测量值存在误差；②实验过程中关阀操作为手动完成，难以实现同时、迅速关闭起终点阀门，造成实际管存计算值不够精确；③优化算法本身具有局限性，对全局最优值的搜索能力有待提高。

4 结论及展望

通过研究输气管道不完全堵塞工况下沿程压力分布特点，使用压力特性曲线法定位管道堵塞位置。研究结果表明：

1）压力特性曲线法仅通过测量管道堵塞稳定工况和关阀工况下管道起终点压力、流量数据，即可定位不完全堵塞位置，方法简单，易于实现。

2）在理论分析基础上，提出将堵塞定位问题转化为参数优化问题并使用PSO、GA、SAA 算法进行求解。结合室内实验分析结果可知，3 种算法均可实现堵塞定位，且PSO算法定位效果最好。

3）压力特性曲线与最优化方法相结合的思路，在输气管道不完全堵塞定位问题的可行性和适用性较高，具有良好的应用前景。

为进一步提高不完全堵塞定位精度及速度，可从以下3个方面考虑：

1）选用搜索能力更强的优化算法。

2）采用管网仿真技术求解理论沿程压力分布曲线，并采用数值积分方法计算理论管存。

3）若管道无法进行关阀测试，可从分析不同堵塞稳定工况下管存变化量的特点来定位堵塞点。