力量训练负荷和肌肉疲劳对表面肌电非线性参数的双重调节

许全盛，白茹雪，李世明

力量训练负荷和肌肉疲劳对表面肌电非线性参数的双重调节

许全盛1，白茹雪1，李世明2*

1.燕山大学，河北秦皇岛 066004；2.中国海洋大学，山东青岛 266100

目的：研究力量训练负荷和肌肉疲劳对表面肌电信号非线性参数的作用规律，探索精准力量训练中对肌力、肌肉做功和疲劳因素敏感的非线性指标。方法： 6名受试者在非疲劳和疲劳状态下分别完成徒手至90%最大负荷共7个负重水平的下蹲起动作，采集股四头肌的表面肌电、足底压力和膝关节角数据，提取表面肌电非线性参数分形维、多尺度熵、科尔莫戈诺夫熵、LZ复杂度，由足底压力和膝关节角计算膝关节力矩，对疲劳前后负重蹲起动作过程的肌电参数和膝关节力矩进行回归分析。结果：无论肌肉是否处于疲劳状态，表面肌电的非线性参数均随负重水平增加而增大，但同等负重水平下，肌肉疲劳导致参数降低。其中，科尔莫戈诺夫熵的线性增长性最显著，而分形维的数值稳定性最高，其峰值出现在60%～75%最大负重。结论： 1）骨骼肌系统的复杂度受到肌肉疲劳和肌肉收缩的共同作用，在运用表面肌电非线性参数评价肌肉疲劳时，应消除肌力或关节力矩的影响；2）表面肌电分形维能较好地反映肌肉做功能力，更全面地评估肌肉工作状态，可以作为精准化快速力量训练及肌肉伤病康复治疗的评价指标。

表面肌电信号；力量训练；肌肉疲劳；复杂度；递增负重

在健康中国背景下，人们的健身意愿日益强烈，参与健步走、广场舞、慢跑等有氧运动越来越普遍。相较有氧运动，我国群众无氧运动参与程度较低，尤其是力量练习，尽管力量素质对各年龄段人群的健身活动都很重要，但对多数人而言力量练习的量和强度较难把握。因此，科学的健身指导非常必要，一方面应实时监测肌肉活动状态，如果肌肉疲劳了仍继续练习容易造成肌肉和关节的损伤；另一方面，应控制好练习量和强度，量和强度过大容易受伤，过小则无法达到最佳的健身效果。检验力量练习对个体的肌肉力量的锻炼效果，可通过表面肌电（surface electromyography， sEMG）信号分析对肌肉活动状态进行评定，预防过度训练导致的肌肉损伤，并使力量练习的量和强度达到必要的水平，实现力量练习的科学化和精准化。

有研究证实，sEMG时域和频域指标在静态收缩和中低强度动态收缩时对肌肉活动的解释效果很好，比如，sEMG平均频率、中值频率随肌肉疲劳的发展呈下降趋势，而均方根振幅、积分肌电等时域指标则呈上升趋势（王健，2001）。此外，肌肉疲劳与肌力、运动负荷、肌电振幅和频谱间存在内在联系：运动负荷改变迫使肌力变化，负荷增大会加速疲劳发展，而肌电振幅和频谱对肌力和疲劳状态具有双重依赖性（李世明，2014）。在中等负荷范围内，肌电振幅随肌力增大和疲劳的产生而增长；频域指标随肌力增大而增大，但随疲劳的发生而降低。因此，当时域指标增大同时频域指标下降可判定肌肉已经疲劳。但当肌肉处于中高强度的动态收缩时，由电极位置、动作电位传导速度、肌力以及肌纤维长度等因素带来的变化使sEMG具有高度的非平稳性、非线性和混沌背景（曲峰，2008；González et al.， 2010）。此时，通过肌电时域和频域分析来评估肌肉疲劳具有较大的局限性，在力量训练和健身活动指导方面无法取得满意效果。

有2种方法能够克服生理信号的非平稳性和非线性：1）时频分析法，根据信号能量在时域和频域的联合分布计算出时变的频域参数，尤其适合检测和评估动态肌肉疲劳（李世明等，2016； González et al.， 2010），但时频分析的计算量大，数值稳定性也较差；2）非线性动力学分析，直接在时域提取信号的近似熵、样本熵（sample entropy，SampEn）、多尺度熵（multi-scale entropy，MSE）、科尔莫戈诺夫熵（Kolmogorov entropy，KE）、LZ复杂度（LZ Complexity，LZC）、分形维数（fractal dimension，FD）、赫斯特指数以及李雅普诺夫指数等非线性特征（刘秉正等，2004）。这些特征从不同角度反映了系统的复杂度，由于生理系统往往表现出复杂的混沌模式和不规则行为，参考这些非线性特征参数有助于研究系统本身。SampEn是最早用于衡量生理系统的复杂性和无序性的参数之一；MSE是在多个离散时间尺度上的SampEn，能够更完整的反映系统信息和时域演化进程（Costa et al.， 2002； Silva et al.， 2015）；Kolmogorov把信息熵的概念精确化，用KE量度系统在运动过程中的混乱或无序程度；Lempel和Ziv提出了一种更一般性的复杂度定义LZC，以反映一个时间序列随其长度的增长出现新模式的速率（刘秉正等，2004）；FD是混沌系统中吸引子几何结构复杂性程度的完全表征；非线性参数与时频参数也无须信号的平稳性假设，但计算量更小。骨骼肌运动单位、动作电位和神经支配具有复杂性，因此，sEMG非线性分析成为研究肌肉系统的有力手段（Liu et al.， 2005），尤其是肌肉在中高强度的动态收缩时，非线性分析相比传统时域和频域分析具有明显优势。

根据生理系统的复杂性理论，健康系统对复杂和不良环境的调节适应能力更强，复杂度更高，相反，病理和衰老系统的信息量由于生理控制能力退化而下降，复杂度降低（Costa et al.， 2002； Goldberger et al.， 2002； Silva et al.， 2015）。对肌肉系统而言，肌肉疲劳时力量输出调节受损，系统处于“病态”，无论是静态还是动态疲劳，sEMG非线性参数大体呈下降趋势（Ancillao et al.， 2014； Kathick et al.， 2018）。但许全盛等（2017）发现，MSE对肌肉疲劳和收缩强度同时敏感，提示在评估肌肉系统复杂性时，必须同时考虑这2个因素。

目前对sEMG肌肉疲劳的研究已较为透彻，结论也比较明朗，但针对肌肉收缩力量（以下简称“肌力”）或收缩强度、运动负荷与sEMG非线性特征关系的研究仍然不足。特别是哪些或哪一种非线性参数能同时对肌肉疲劳、运动负荷以及肌肉做功能力的变化更为敏感尚不清楚，这在一定程度上限制了sEMG分析对力量练习和健身活动的指导作用。因此，本研究通过递增负重下蹲实验，研究力量训练中运动负荷、疲劳因素与sEMG 4类典型非线性参数（MSE、KE、LZC和FD）间的协同变化规律，探索力量训练中sEMG敏感指标。

1 研究对象与方法

1.1　实验对象

以体育专业6名男生为受试者，年龄（20.7±1.3）岁，身高（1.73±0.03）m，体质量（65.90±2.28）kg。所有受试者均为右利手，身体状况良好，无任何运动损伤，实验前24 h未熬夜，未饮酒，未参与任何形式的剧烈运动，并在实验前签署了知情同意书。

1.2　实验数据采集

1.2.1最大力量测试

采用McNeely推荐的间接测试法测试受试者蹲起的最大负重，具体步骤为：1）采用受试者能轻松重复5～10次的重量进行热身；2）休息2 min；3）重量增加10%～20%，尽量多的重复，使受试者在2～20次达到疲劳；4）利用公式计算最大负重。计算公式为：最大力量（RM）=［（0.033×重复次数）×重量］＋重量，其中，重复次数指蹲起的次数，重量指蹲起的重量，如果受试者的重复次数超过10次，则休息10 min后，将重量再增加10%～20%，再次测试。

1.2.2非疲劳状态下递增负重实验

选择负重下蹲（包括下蹲和起立2个阶段）动作完成数据采集，便于控制实验条件使肌力和关节力矩在较大范围内变化，便于大量重复操作。准备姿势为：将杠铃置于颈后，双手抓握杠铃，身体挺直，两眼平视前方，两脚与肩同宽，足尖外斜约15°，负重下蹲后接着负重起立还原。实验员指导受试者依次在三维测力台上完成从0% 1RM（徒手）、15% 1RM、30% 1RM、45% 1RM、60% 1RM、75% 1RM和90% 1RM共7个负重水平的下蹲起动作，其中30% 1RM、45% 1RM对应力量耐力练习模式，60% 1RM、75% 1RM对应爆发力量练习模式，90% 1RM对应最大力量练习模式。每次动作重心都下蹲到最低位（深蹲）后，再全力快速蹬起，每个负重水平重复做3次，前2次为熟悉性操作，在实验员的指导下感受动作速度和幅度，最后1次时采集实验数据，每个负重水平间休息2 min。实验过程中完成如下测量：1）采用三维测力台测试双脚受力及压心变化，采样频率1 000 Hz；2）采用Simi-Motion运动录像解析系统在矢状面内对动作过程进行拍摄，拍摄频率100 Hz，采集右侧膝关节角和角速度；3）采用JE-TB0810八通道肌电系统采集右侧腹直肌、股内侧肌、股外侧肌的sEMG信号，采样频率1 000 Hz。实验时将测力台的触发信号输入肌电仪和运动录像解析系统，实现硬件同步。

1.2.3疲劳实验

采用部义峰等（2013）研究中的蹬车方案，利用功率自行车给受试者施加递增负荷至疲劳状态。受试者手戴心率遥测表，首先在零负荷下蹬踏功率自行车（MONARK824型）1 min，适应50转/min的转速后进入正式测试。起始负荷50 W，每3 min递增50 W，转速保持50转/min，负荷递增到200 W后不再增加。每一负荷结束前5 s记录自觉用力评分指数（rating of perceived exertion，RPE）等级及心率。如果受试者经鼓励督促仍不能按规定强度运动持续10 s以上，并同时满足达到预期最大心率（220-年龄）和RPE＞18，便认为受试者股四头肌已进入疲劳状态，停止运动。

1.2.4非疲劳状态下递增负重实验

疲劳实验后立即进行负重下蹲起实验。疲劳后受试者很难连续力量耐力和爆发力量练习，随着实验的进行，疲劳程度逐渐降低，而且不同受试者的恢复能力存在差异，因此，在疲劳状态下只进行1～2个负重水平的测试，要求与非疲劳状态下测试一致。完成后休息足够长的时间，使机体完全恢复后，再次通过功率自行车达到疲劳状态，进行下一个负重水平的测试。

1.3　肌电信号采集与预处理

采用八通道肌电采集系统（JE-TB0810，中国）采集sEMG信号，肌电仪佩戴于受试者腰部，电极片采用Ag/AgCI一次性使用圆形心电电极（上海钧康医用设备有限公司），直径2.5 cm；3个电极成等边三角形贴于待测肌肉肌腹沿肌纤维走向的方向上。放置电极贴前分别用磨砂纸和医用酒精擦拭皮肤以减小电阻。肌电仪配备截止频率为10 Hz的2阶巴特沃兹高通滤波器和截止频率为500 Hz的低通滤波器，以消除环境噪声和运动伪迹的影响，信号采样频率1 000 Hz，增益119 dB，共模抑制比＞100 dB，输入阻抗＞1012Ω，输入范围±3 mV。将采集的sEMG信号导入计算机，利用MATLAB 2014a对股直肌、股内侧肌和股外侧肌的疲劳前后7个负重级别的sEMG信号进行预处理，设计2阶椭圆数字陷波器滤除50 Hz工频干扰后，将每位受试者共42段原始sEMG信号（3块肌肉在非疲劳和疲劳后的7级负荷）转换为待处理的时间序列数据，备后续分析使用。

1.4　参数计算

选择MSE、KE、LZC和FD 4种具有代表性的非线性特征参数，利用MATLAB直接在sEMG信号时域提取参数值，从不同角度反映肌肉系统复杂度。利用逆向动力学算法由采集的足底测力数据计算负重下蹲动作的膝关节力矩，以此反映肌肉收缩强度或肌力水平。

1.4.1MSE

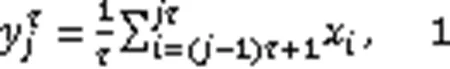
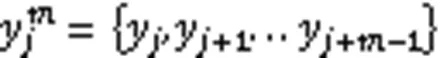
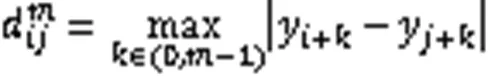
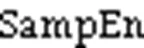
本研究将SampEn在所有尺度上的平均值（mean multi-scale entropy，MMSE）作为MSE复杂度测量。研究表明，MMSE相比单一尺度的SampEn能更有效地识别肌肉动态疲劳（许全盛等，2017）。

1.4.2KE

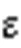
1.4.3LZC

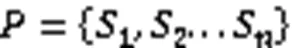
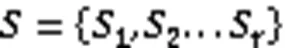
3）当趋于∞时几乎所有的（）都会趋于一常数，即：

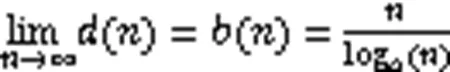
其中，（）为序列的渐进行为，为字符串中不同字符的个数。用（对（进行归一化得：

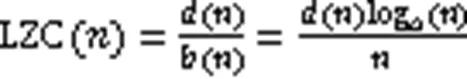
1.4.4FD

分形物体的基本特征是其长度、面积或体积取决于测量尺度。将sEMG信号视为一维曲线，FD就是曲线复杂性的特征，FD最常用的是盒型算法（box counting）（刘秉正等，2004）和Katz算法（Katz， 1988）。Liu等（2005）研究认为，Katz算法对信号的随机性最敏感，对运动相关信号的量化能力最强。因此，本研究选择Katz算法量化sEMG复杂性变化，其原理为：

对一段连续平面曲线，FD的一般定义为：

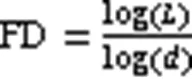
其中，是曲线的总长度，是曲线的直径（平面范围）。对一段波形，它们是由一系列点（x，y）的有序集，总长度是连续点之间距离的之和：

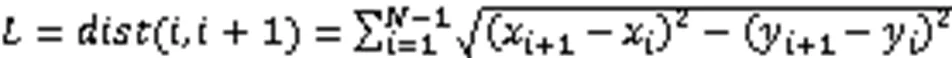
其中，为序列长度，即x和y的个数。由于波形有一个自然的起始点，平面范围可以看作是起始点（1，1）与波形的任何其他点（点）间的最远距离，即：

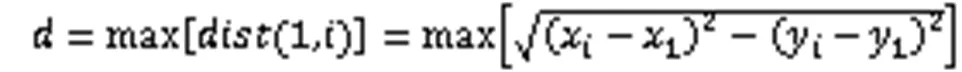
对一维离散波形，FD计算需归一化为平均步长/，代入公式（8）可得Katz的FD：

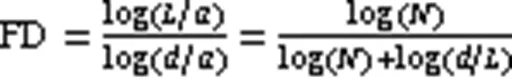
其中，=/是曲线中的步数。对单调进行“向前”的平面曲线，FD介于1.0（直线）和1.5（高尖峰波）之间。真实波形永远不会变得足够复杂来填充一个平面，因此波形永远不会有接近平面2.0维数FD。

1.5　膝关节力矩与非线性参数和疲劳因素的回归分析

本研究通过膝关节角运动学数据、足底测力台数据，利用逆向动力学算法计算得到膝关节合力矩，膝力矩反映膝关节肌群的肌力贡献，大小取决于肌肉收缩强度。膝力矩计算的核心是牛顿-欧拉方程，其中膝关节角度通过运动录像解析系统根据髋膝踝骨性标志点的坐标计算得到，下肢关节转动惯量根据受试者身高、体质量，通过运动解析系统中人体环节参数模型获得。测力台数据包括足底压力和转矩，将测力台关于矢状面受力和冠状轴转矩数据，和转动惯量、膝关节角一起代入牛顿方程得到膝关节力矩，其数值求解过程通过MATLAB多刚体力学工具箱实现。

利用MATLAB对所有受试者在非疲劳和疲劳态下分别完成负重下蹲动作过程膝关节力矩的平均值与股直肌、股内侧肌和股外侧肌sEMG非线性参数值间的相关性进行统计分析。通过绘制非线性参数随膝关节力矩的变化的散点图，运用最小二乘法对散点图进行线性回归并计算其回归系数、可决系数2和统计量，探究对力量练习负荷和疲劳程度敏感的sEMG指标，回归方程如下：

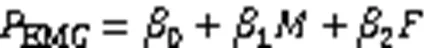
2 研究结果

2.1　时域波形

股直肌、股内侧肌和股外侧肌是对负重蹲起动做贡献最大的3块肌肉。本研究中每位受试者在非疲劳状态和疲劳状态完成负重下蹲动作各产生21段肌电信号（7种负重水平，3块肌肉），以受试者马XX股内侧肌疲劳前后的原始肌电波形为例，无论是非疲劳状态还是疲劳状态时，肌电振幅和信号时长均随负重水平从0% 1RM（徒手）至90% 1RM而递增；与非疲劳状态相比，负重较轻时振幅有所增大，但负重较大时并不显著（图1）。

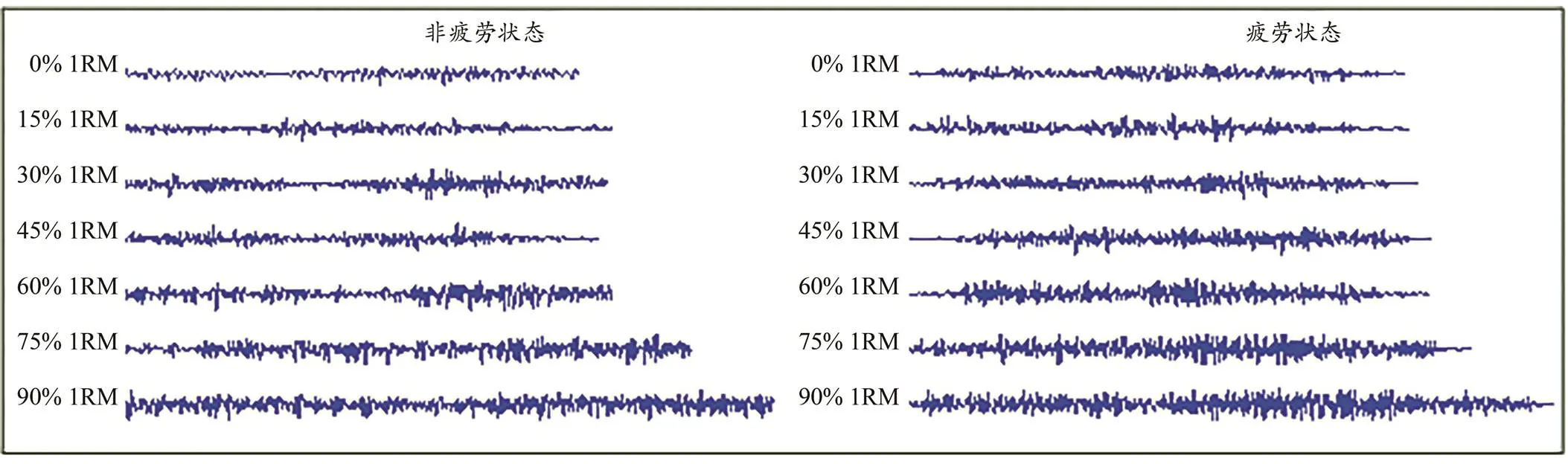
图1　受试者马XX在非疲劳状态（左）和疲劳状态（右）下不同负重时股内侧肌的原始肌电波形

Figure 1. Raw sEMG of Vastus Medialis of Subject Ma XX in Fatigue-Free（Left） and Fatigue State（Right） at Different Loads

2.2　sEMG参数

6名受试者股直肌、股内侧肌和股外侧肌sEMG 4个非线性参数在疲劳和非疲劳状态下的计算结果（平均值±标准差）中MMSE计算时容许误差取0.2，嵌入维取2，时间延迟取1，考虑到受试者完成下蹲起动作记录的长度大多在1 500～2 000 ms，MSE最大时间尺度选择50（表1）。

2.3　膝关节力矩

根据逆向动力学算法得到6名受试者的膝关节力矩在每个负重水平的所有最大值的平均值和标准差（表2）。

以受试者马XX疲劳状态和非疲劳状态的膝关节力矩随时间变化为例，膝力矩最大值和平均值均随负重增加而增加，由于完成动作的难度随负重逐渐增大，膝关节角速度逐渐变慢，膝力矩发挥作用的时长逐渐增加（图2）。

2.4　膝力矩和疲劳对肌电参数的影响

2.4.1sEMG非线性参数随递增负重水平的变化

以股内侧肌为例，将疲劳状态和非疲劳状态时各参数的平均值和标准差数据绘制成按负重水平递增的柱状图（图3）。从徒手到最大负重90% 1RM全部7个负重水平，疲劳后的sEMG非线性参数均显著低于非疲劳状态下的数值。无论是疲劳还是非疲劳状态，4种参数变化趋势基本类似，总体上均随负重递增而递增。其中，KE的线性增长性最显著，MMSE和LZC在30% 1RM负重时稍有下降，但LZC在75% 1RM时稍大于90% 1RM，而FD在60% 1RM和75% 1RM时数值接近，但在90% 1RM时有明显下降；从数值稳定性看，MMSE在不同受试者间个体差异最大，LZC次之，而FD的方差最小，表现最为稳定。

为观察肌电参数在不同肌肉间的变化情况，将股直肌、股内侧肌和股外侧肌的MMSE随负重水平的变化绘制为柱状图（图4），3块肌肉的肌电参数在不同负重水平下的排序并不完全相同，但疲劳前后的总体变化趋势基本一致，其他参数在不同肌肉间变化情况与MMSE类似。

由图5可知，肌电参数与膝关节力矩总体呈正相关，同时，疲劳状态下膝关节力矩和肌电参数均降低（数据点在非疲劳时的左下方）。由图可见，MMSE和LZC的线性性较差，30% 1RM和45% 1RM负重下疲劳和非疲劳状态MMSE和LZC数值有所交叠，而KE和FD增长的线性性更明显。进一步观察可见LZC和FD的峰值都出现在75% 1RM，但FD在60% 1RM时的数值比LZC更加接近75% 1RM。

2.4.2sEMG非线性参数与膝关节力矩的回归分析

将6名受试者从徒手至90% 1RM共7个负重水平的sEMG参数和膝关节力矩的对应关系绘制成散点图（图6）。其中疲劳状态和非疲劳状态的数据点各由42个散点组成，根据最小二乘法对散点数据进行线性回归。结果发现，疲劳状态数据点的回归线均位于非疲劳状态的下方；从散点的分布范围看，MMSE最大，FD最为集中，而KE和LZC介于两者之间；从拟合的直观效果看KE的线性性最显著。

表1　受试者肌电非线性参数汇总表

表2　受试者的膝关节力矩最大值统计

总结4类非线性参数与膝关节力矩的回归方程的可决系数（2统计量）、统计量以及回归系数，结果1全部为正，而2全部为负，说明sEMG的非线性参数与肌力或力矩呈正相关而与疲劳程度的呈负相关。KE的2统计量和统计量显著高于其他3类参数，说明其线性拟合的效果最佳（表3）。

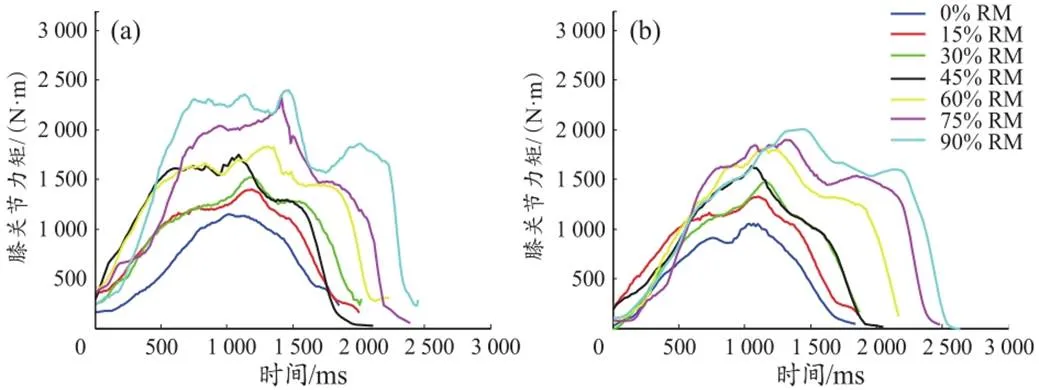
图2　受试者马XX在非疲劳状态（a）和疲劳状态（b）递增负重练习的膝关节力矩

Figure 2. Knee Joint Torque of Subject Ma XX in Fatigue-Free （a） and Fatigue State （b） at Different Loads

3 分析与讨论

力量素质对各年龄段人群都很重要。力量训练过程中，练习者直观感觉是运动负荷增大迫使肌肉加强收缩，以产生更大肌力或力矩来完成动作，同时，负荷增大也会加速疲劳发展。但无论是健身爱好还是专业训练，掌握力量练习的量和强度仅凭感觉是不够的，因为人的主观感受是整体性的，尤其在专项力量训练中很难形成某块肌肉或某个肌肉群的精确感觉，所以需要有科学的量化指导。通过sEMG信号对肌肉状态进行监测评估可以具体到某一块肌肉，由力量训练负荷和练习模式不同所带来的肌肉收缩力、收缩速度、关节力矩、输出功率、疲劳程度的变化信息都蕴含在sEMG信号中，通过时域、频域、时频域以及非线性参数定量得以反映。利用sEMG对肌肉活动状态进行评定，能有效预防过度训练导致的肌肉损伤，制定最佳的练习量和强度，使肌肉力量获得最大限度的超量恢复。

图3　股内侧肌sEMG非线性参数随递增负重水平的变化

Figure 3. The Variation of sEMG Nonlinear Parameters in Medial Femoral with Increasing Load Level

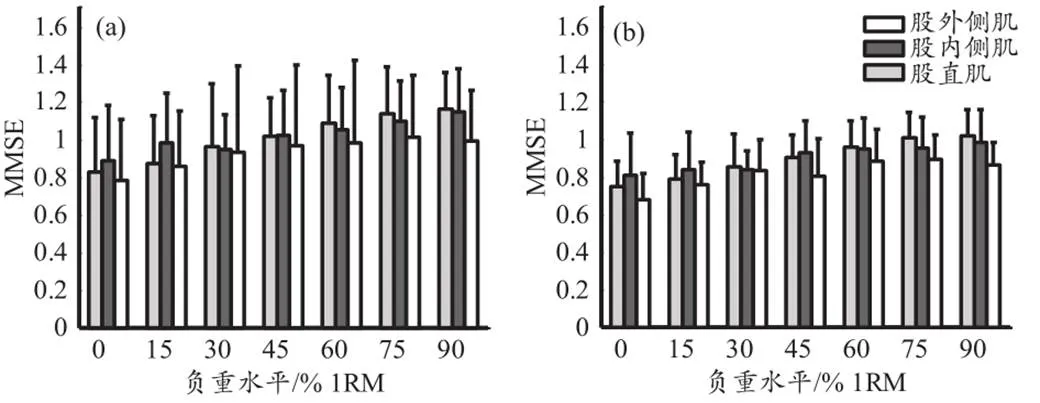
图4　股直肌、股内侧肌和股外侧肌在非疲劳状态（a）和疲劳状态（b）sEMG平均多尺度熵随负重水平的变化

Figure 4. The Variation of Mean Multiscale Entropy of sEMG with Load Level in Rectus Femoris， Medial Femoris and Lateral Femoris in Fatigue-Free （a） and Fatigue State （b）

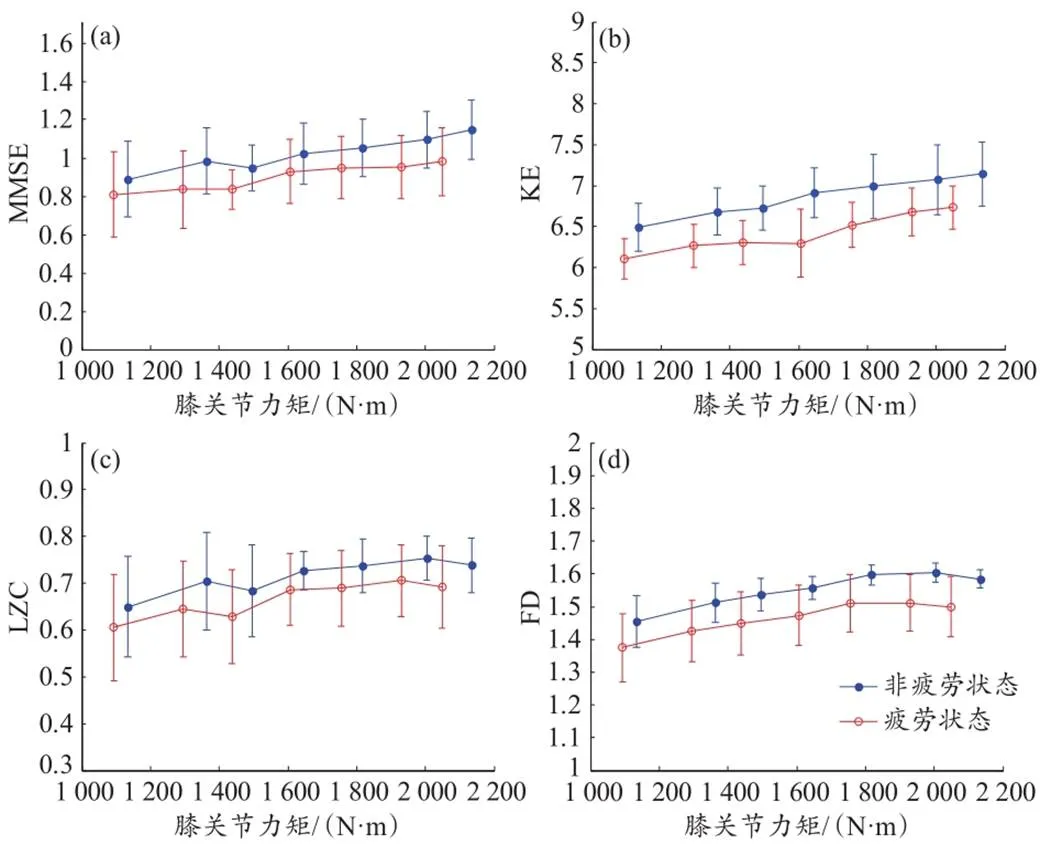
图5　 sEMG非线性参数随膝关节力矩最大值的变化

Figure 5. Variation of Nonlinear Parameters of sEMG with the Maximum Knee Joint Torque

肌力与骨骼肌运动单元的募集程度呈正相关，运动单元募集和发放率最大时形成最大肌力，sEMG信号是骨骼肌运动单元异步发放产生的多个脉冲串叠加的结果，运动单元越多，产生的sEMG信号越复杂。当肌肉被激活并施加负荷时，由此产生的sEMG信号的复杂性随肌肉收缩加剧而增加。因此，可以推测肌肉系统为适应收缩强度增大、肌力增加的变化使sEMG的复杂度也随之增大。本研究选择的sEMG 4种非线性参数从不同侧面反映了肌肉系统的复杂度。股四头肌是膝关节控制肌群中最重要的大肌肉，在屈膝和伸膝过程中分别完成退让式收缩和克制性收缩。图2表明，随着负重等级增大，以股四头肌为主的伸肌群收缩强度增大，以产生更大的肌力和膝力矩。表3、图3、图4、图5中系数1都说明了sEMG 4种非线性参数值与负重水平或膝力矩正相关，也证明了肌肉收缩强度和肌力水平的确与复杂度呈正相关，但在图5中FD和LZC的峰值并没有出现在最大负重上。

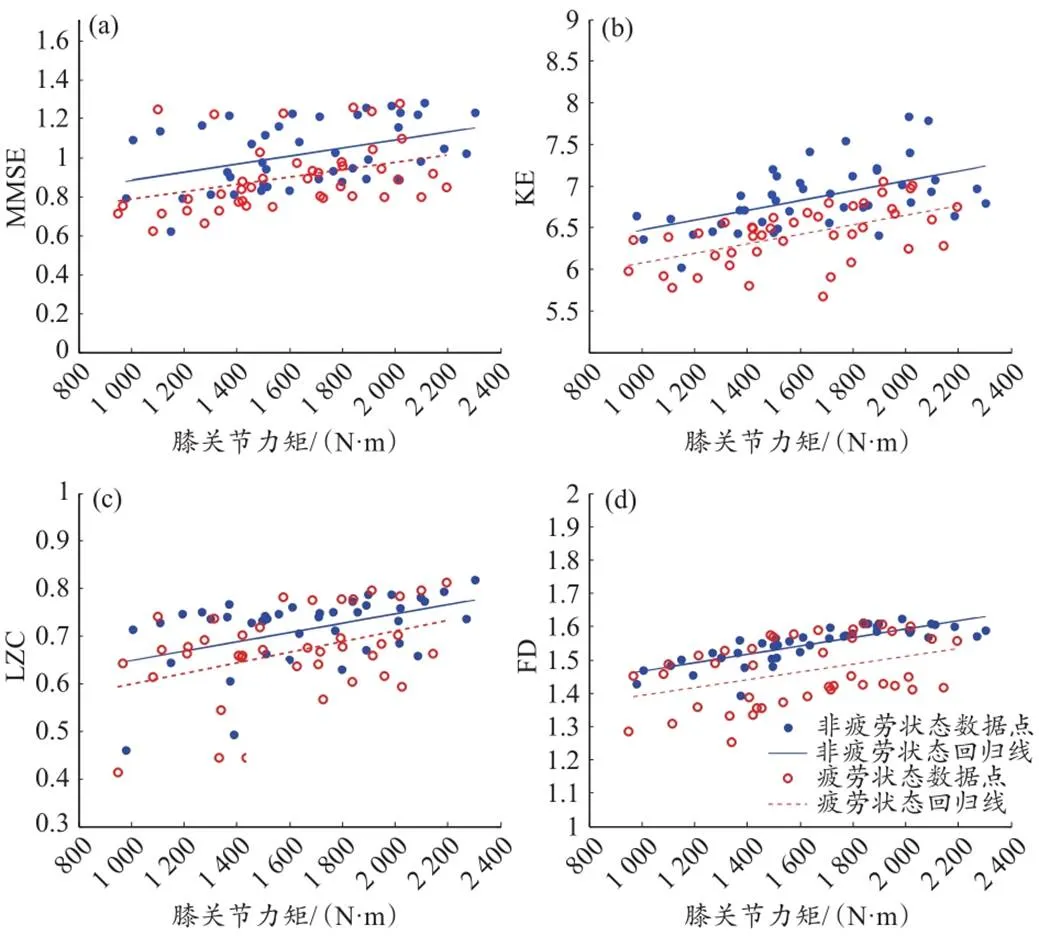
图6　 sEMG非线性参数与膝关节力矩的回归结果

Figure 6. Regression Results of sEMG Nonlinear Parameters and Knee Joint Torque

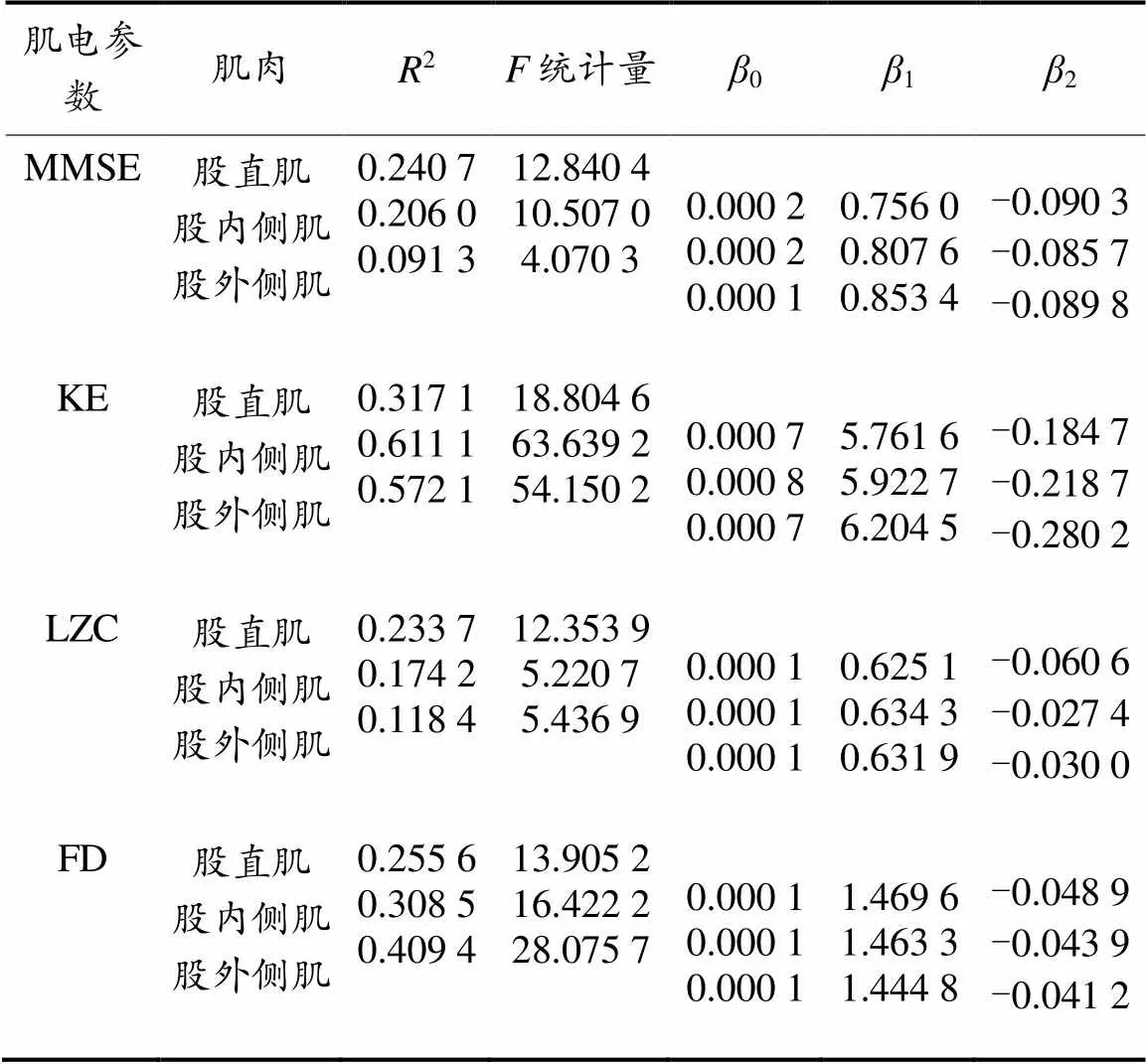
表3　 sEMG非线性参数对膝关节力矩回归统计量

健康系统对复杂和不良环境的调节适应能力更强，而病态和衰老系统的信息量由于生理控制能力退化而下降，表现为复杂度降低（Costa et al.， 2002； Goldberger et al.， 2002； Silva et al.， 2015）。对肌肉系统而言，肌肉疲劳时力量输出调节受损，系统可视为处于“病态”。本实验结果证实，疲劳时肌肉活动的复杂度的确降低。其中，图3、图4说明在同等负荷下，疲劳后的sEMG 4类非线性参数值均显著低于非疲劳状态；疲劳抵消了一部分非线性参数随膝力矩增长的趋势（图5），同时，疲劳引起了骨骼肌最大随意收缩力量和输出功率下降，同等负重下的膝关节力矩均有不同程度的降低；6名受试者的平均值的变化趋势（图3、图4、图5）和42个样本点的线性回归，疲劳状态数据点的回归线均位于非疲劳状态的左下方（图6），同样说明疲劳抵消了非线性参数随负重的一部分增长；系数2则说明，sEMG非线性参数与疲劳程度呈负相关（表3）。综上，本研究认为sEMG非线性参数对力量训练负荷和疲劳状态具有双重依赖性，或者说肌肉系统复杂度对肌力和疲劳因素同时敏感。

肌力的产生和肌肉收缩速度的结合将输出肌肉功率。对sEMG非线性参数与肌肉做功之间联系的研究较少。Liu等（2005）对受试者手持测力装置时脑电信号分析，脑电FD与所测握力呈线性相关；Gupta等（1997）研究表明，sEMG FD对肌力的大小和收缩速度都很敏感，与肌肉的运动潜力密切相关；而Ancillao等（2014）发现，纵跳高度与FD正相关。人体纵跳高度与下肢肌肉爆发力也就是肌肉功率密切相关，因此，可推断FD是一个对肌力和肌肉功率同时敏感的指标，本实验结果也证实了这一点。从图5可见，FD峰值都出现在60% 1RM附近，而LZC出现在75% 1RM，考虑到60%～75% 1RM的力量训练接近爆发力量练习模式，即肌力和肌肉收缩速度的乘积最大，肌肉输出功率最大的模式，而中低负荷时（30% 1RM和45% 1RM）肌肉快速收缩和高负荷时（90% 1RM）肌肉慢速收缩分别属于力量耐力和最大力量练习模式，这2种情况下肌肉输出功率都无法达到最大值接近力量耐力模式，因此，FD和LZC属于与肌力和肌肉功率同时敏感的指标，但FD更能反映爆发力量素质。

进一步分析可知，由于FD和LZC的峰值不在最大负重水平上，破坏了公式（12）的线性假设，所以表3中FD和LZC的2和统计量均显著小于线性拟合效果最好的KE，而图5也更直观地反映了FD对肌肉功率的敏感性。

4 结论与建议

骨骼肌系统的复杂度受到肌肉疲劳和收缩强度的双重调制，在运用非线性参数评价肌肉动态疲劳时，应同时考虑肌肉收缩强度的影响。

FD能更全面地反映骨骼肌的工作状态。在实际工作中，FD可作为快速力量训练效果检验、运动员选材以及肌肉伤病康复治疗的评价指标。

sEMG信号非线性参数提取在时域直接进行，计算复杂度较小，且无须信号的平稳性假设，有利于对力量练习者的肌肉活动状态的实时监测和评估，实现力量训练的科学化、定量化和精准化。

部义峰，李世明，2013. 递增负荷诱发肌肉疲劳过程中肌肉sEMG与负荷的非线性关系研究［J］. 山东体育学院学报，29（6）： 47-52.

李世明，2014.运动技术诊断概论［M］.北京：科学出版社.

李世明，许全盛，翟佳丽，等，2016.基于表面肌电时频分析的递增负荷诱导肌肉周期动态疲劳估计［J］.中国体育科技， 52（3）：48-56.

刘秉正，彭建华， 2004.非线性动力学［M］.北京：高等教育出版社.

曲峰，2008.运动员表面肌电信号与分形［M］.北京：北京体育大学出版社.

王健，2001.静态负荷肌肉疲劳过程中肌肉功率谱转移特征［J］.中国运动医学杂志，20（2）： 199-201.

许全盛，李世明，季淑梅，2017.基于sEMG多尺度熵分析的递增负荷诱导肌肉动态疲劳评估［J］.天津体育学院学报，32（4）： 344-349.

ANCILLAO A， GALLI M， RIGOLDI C， et al.， 2014. Linear correlation between fractal dimension of surface EMG signal from rectus femoris and height of vertical jump［J］. Chaos Soliton Fract， 66： 120-126.

COSTA M， GOLDBERGER A L， PENG C K， 2002. Multiscale entropy analysis of complex physiologic time series［J］. Phys Rev Lett， 89（6）： 1-4.

GOLDBERGER A L， PENG C K， LIPSITZ L A， 2002. What is physiologic complexity and how does it change with ageing and disease？［J］. Neurobiol Aging， 23（1）： 23-26.

GONZÁLEZ M， MALANDA A， NAVARRO A， et al.， 2010. EMG spectral indices and muscle power fatigue during dynamic contractions［J］. J Electromyogr Kinesiol， 20（2）： 233-240.

GUPTA V， SURYANARAYANAN S， REDDY N P， 1997. Fractal analysis of surface EMG signals from the biceps［J］. Int J Med Inform， 45（3）： 185-192.

KATHICK P A， GHOSH D M， RAMAKRISHNAN S， 2018. Surface electromyography based muscle fatigue detection using high-resolution time-frequency methods and machine learning algorithms［J］. Comput Methods Programs Biomed， 154： 45-56.

KATZ M J， 1988. Fractals and the analysis of waveforms［J］. Comput Biol Med， 18（3）：145-156.

LIU J Z， YANG Q， YAO B， et al.， 2005. Linear correlation between fractal dimension of EEG signal and handgrip force［J］. Biol Cybern， 93（2）：131-140.

SILVA L E， CABELLA B C， NEVES U P， et al.， 2015. Multiscale entropy-based methods for heart rate variability complexity analysis［J］. Physical A， 422（1）： 143-152.

Strength Training Load and Muscle Fatigue Cooperatively Modulates the Nonlinear Parameters of Surface Electromyography

XU Quansheng1，BAI Ruxue1，LI Shiming2*

1.Yanshan University, Qinhuangdao 066004, China;2.Ocean University of China, Qingdao 266100, China.

Objective: This paper is aimed to study the effect of strength training load and muscle fatigue on nonlinear parameters of sEMG signal, and to explore the nonlinear indexes sensitive to muscle strength, muscle work and fatigue factors in precision strength training. Methods: Six volunteers were enrolled to perform weight-bearing crouching experiment under seven loading level from zero to 90% maximum load in fatigue and fatigue-free condition, respectively. The sEMG, plantar pressure and knee joint angle data of quadriceps femoris were collected; the nonlinear parameters of sEMG, including fractal dimension, multi-scale entropy, Kolmogorov entropy and LZ complexity, were extracted, and the knee joint torque was calculated from plantar pressure and knee joint angle by inverse dynamics; the nonlinear parameters of sEMG and knee joint torque in weight-bearing squatting were analyzed by regression analysis. Results: Whether the muscles are non-fatigued or fatigued, the nonlinear parameters increased with the increase of weighting load level, but at the same load level, muscle fatigue lead to lower parameters. The linear increase property of Kolmogonov entropy was the most significant, and the numerical stability of fractal dimension was the best, and the peak value appeared between 60% and 75% of the maximum load. Conclusions: 1) the complexity of skeletal muscle system is affected by muscle fatigue and muscle contraction, hence the influence of muscle strength when using nonlinear parameters to evaluate muscle fatigue should be eliminated; 2) fractal dimension can reflect the ability of muscle power to some extent, and evaluate the working state of skeletal muscle more comprehensively, therefore it could be used as an evaluation index of accurate explosive strength training and rehabilitation of muscle injuries.

1002-9826（2022）08-0083-08

10.16470/j.csst.2020081

国家体育总局科技服务项目（2017B047）

许全盛（1973-），男，博士，硕士研究生导师，主要研究方向为生物医学信号处理、运动生物力学，E-mail：123122122@qq.com。

通信作者简介：李世明（1969-），男，教授，博士，硕士研究生导师，主要研究方向为运动生物力学，E-mail：leesm0503@ 163.com。

G808.1

A

（2019-12-19；修订日期：2022-03-23； 编辑：丁合）