基于滑模变结构控制的光电稳定平台控制策略研究

2022-08-27郭擘柯芳余潇高歆杨孙爱鲜

兵工学报 2022年8期

郭擘，柯芳，余潇，高歆杨，孙爱鲜

(西南技术物理研究所，四川成都 610041)

0 引言

光电稳定平台是指安装在光电跟踪系统上使用伺服控制方法减弱光电跟踪系统因基座运动受到的扰动乃至完全隔离扰动的装置。光电稳定平台被广泛地应用于车载、机载、弹载、舰载设备中，从实现的形式上又可分为与跟踪系统完全独立设计和共用同一套伺服驱动装置两种不同方案。视轴稳定技术是光电稳定平台中的关键技术，目前应用较多的视轴稳定控制方法主要分为两类：一种是以PID控制为代表的传统控制方法，PID法已有多年研究历史，理论研究和实际应用的技术均十分成熟，但缺点是无法适应被控对象参数发生改变的情况，同时对于系统运行时受到的随机扰动无法做到有效抵抗。另一类是各种先进控制方法，如自适应控制等。这些方法大多有不错的鲁棒性和抗扰动能力，还能适应系统中存在的非线性特性，相比传统控制方式性能更好，系统更稳定，但是这些方法目前大多在仿真阶段，在实际工程中应用有一定阻碍。

文献[17]提出了一种改进的增量式PID算法控制直流电机，对增量式PID的增量步长加以限制，使电机可以平稳变速，这种控制方式需要得到精确的对象参数，并且限制了系统控制量的同时也限制了系统的快速性。文献[18]使用模型参考自适应控制补偿了光电稳定平台受到的扰动，提升了系统的跟踪性能，增强了抗扰动能力，但是依赖于找到设计参数与输出误差之间的关系。文献[19]提出了神经网络与自抗扰控制结合的控制方法，提升了系统的抗扰能力，但是研究只在理论与仿真阶段。

变结构控制是一种适用于线性及非线性系统的控制系统设计方法，可以用于控制系统的调节、跟踪、自适应及不确定系统。它具有一些优良特性，尤其是对加给系统的摄动和干扰有良好的自适应性，且具有物理实现简单、便捷的优点，从20世纪90年代以来，这种设计方法受到了国内外的广泛重视，得到了很快发展。因此，本文提出用变结构控制的方法来实现光电稳定平台的视轴稳定。

本文提出一种转台三闭环控制系统的速度环采用滑模变结构策略的控制方法，相比于传统的速度环控制策略而言稳定精度更高，也具有对摩擦力矩等扰动更强的自适应能力，使系统可以在各种场合正常运行。以光电稳定平台的方位轴为被控对象设计了滑模控制器，对光电稳定平台进行仿真研究，并与传统控制方法下的系统性能进行对比，验证本文提出的滑模变结构控制器可以改善控制系统的性能，为提升复合轴系统联合跟踪精度奠定了基础。

1 光电稳定平台数学模型

本文研究的光电稳定平台由包含方位轴和俯仰轴的二维伺服转台实现，由于两个轴相互独立，伺服控制方法相似，本文选择方位轴为研究对象。对于高精度的伺服转台，方位轴系与俯仰轴系间有足够的正交度，跟踪回路在方位轴与俯仰轴之间仅有一个俯仰角的正割补偿的变换关系，在进行转台的整体设计时可以代入正割补偿做修正，同时不影响单轴系统的设计结果。典型的转台方位三闭环控制系统结构如图1所示。

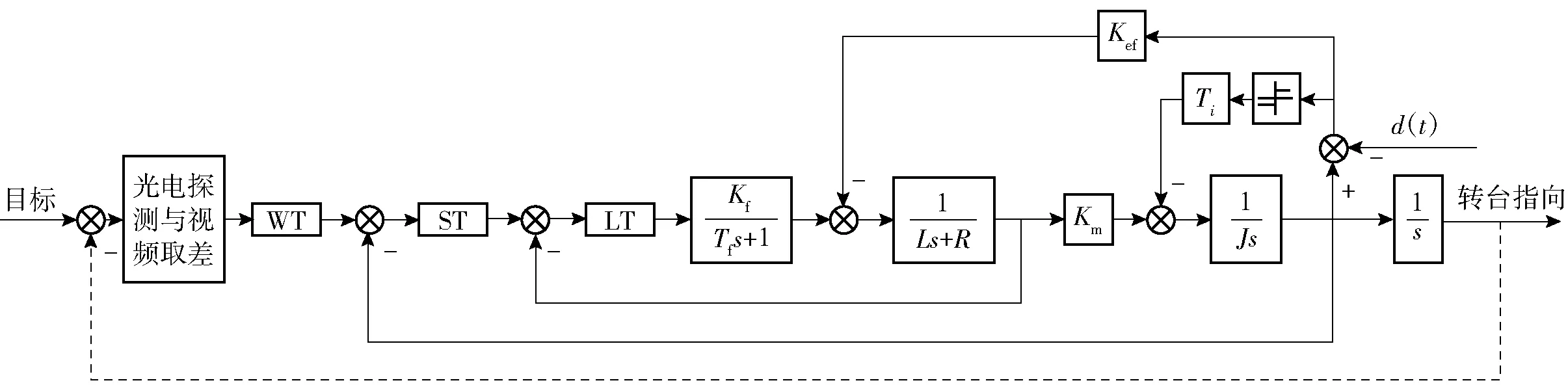
图1 转台方位轴控制系统原理框图Fig.1 Schematic diagram of turntable azimuth axis control system

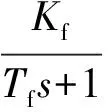
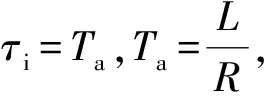
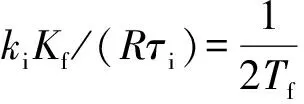
(1)

得到电流环开环传递函数

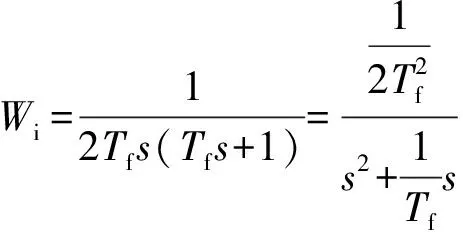
(2)

此时电流环闭环传递函数为

(3)

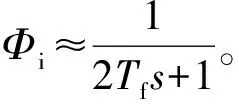
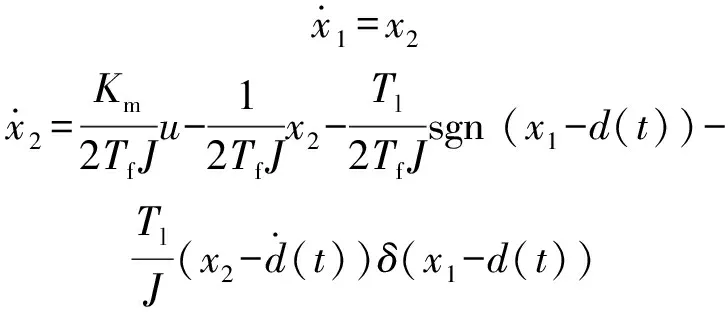
(4)

式中：为系统角速度；为角加速度；为速度环控制器输出；(·)为冲激函数。

2 控制器设计

滑模变结构控制是一种通过切换控制输出迫使控制系统运行在设定好的状态，这种方法具有很强的鲁棒性、抗扰动能力。在滑模控制中，可以通过滑模面来设定系统的运动轨迹，在滑模面的不同侧面控制律可以通过改变自身的结构促使滑模面之外系统状态向着滑模面运动，到达滑模面后控制律也可以通过改变结构使系统保持在滑模面上运动。与许多先进控制理论在物理上难以实现不同，滑模变结构控制技术原理简单，利于在工程中使用。但同时控制律的不连续高频切换会使系统输出产生剧烈的抖振，对控制精度产生较大影响，甚至有可能损坏硬件，如何削弱抖振也是变结构控制器研究的重点。

2.1 速度环滑模变结构控制器设计

滑模控制的基本思路是根据系统的状态改变控制器本身的结构，使系统状态按照预设的轨迹运动。设计人员可以预先设定滑模面轨迹，在系统受到扰动或被控对象参数摄动时不会偏离预设轨迹，使得滑模控制系统具有很强的抗扰能力与鲁棒性。

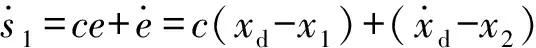
(5)

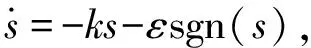
将等式联立，得到控制器的输出：

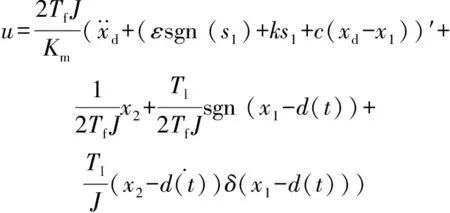
(6)

考虑如下李雅普诺夫函数：

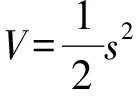
(7)

对该李雅普诺夫函数求导，得

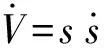
(8)

代入(5)式和滑模面等式，可得

(9)

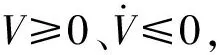
2.2 位置环控制器设计

位置环是实现目标跟踪的跟踪环，位置环控制器采用PID控制方法，参数使用临界灵敏度法整定，画出系统的Bode图，记系统-180°穿越点的幅值裕量和穿越点频率，由公式

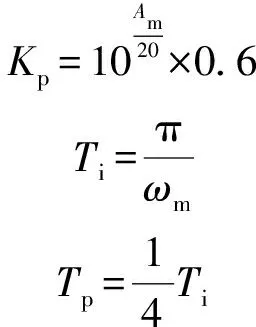
(10)

可得到位置环的PID控制器参数。在光电探测与视频取差环节会出现硬件上的延时，在控制系统中可以等效为纯滞后环节，使得控制系统为非最小相位系统，此时幅值裕量应考查相位为180°的穿越点。

3 仿真实验与分析

3.1 仿真实验所用模型及对象参数

将实际的控制系统建模，得到系统参数=16，=0001 67 s，=175 N·m/A，=175 V/(rad/s)，电机绕组电感=0020 2 H，电机绕组电阻=48 Ω，转动惯量=116 kg·m。将以上参数代入三闭环转台方位轴控制系统，由第1节提到的方法可以设计出系统的电流环控制参数，得到完整的被控对象模型，摩擦力矩取为5 N·m，模拟系统受到的扰动，仿真框图如图2所示。图2中，()为频率为1 Hz、幅值为10°s的正弦扰动角速度。

图2 控制系统仿真模型图Fig.2 Simulation model of control system

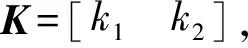
(11)

3.2 稳定性能仿真试验内容

为了验证滑模变结构控制系统应用于光电稳定平台的有效性，以光电跟踪系统的转台方位轴为被控对象，进行与速度环、位置环均采用传统PID控制的系统的对比试验，结合实际工程应用背景，进行以下3项对比试验。

3.2.1 速度环稳定控制对比试验

将跟踪环断开，速度环参考输入为0，仅对比系统速度环稳定误差。

滑模控制系统的稳定误差如图3所示，PID控制系统的稳定误差如图4所示。其中滑模控制系统的稳定误差最大值为5.857×10rad/s，PID控制系统的稳定误差最大值为3.523×10rad/s，滑模控制下的系统稳定误差更小，抵抗扰动的能力更强。

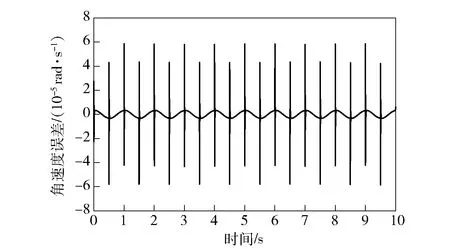
图3 滑模控制器下的速度环稳定误差Fig.3 Stability error of velocity loop under sliding mode controller

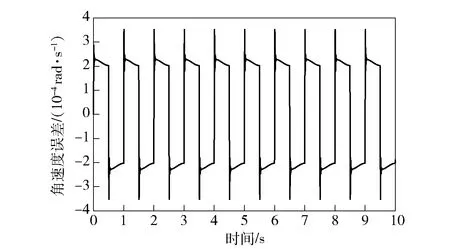
图4 PID控制器下的速度环稳定误差Fig.4 Stability error of velocity loop under PID controller

3.2.2 跟踪环稳定控制对比试验

接入跟踪环，跟踪环参考输入为0°，模拟目标固定的情况，对比系统跟踪环稳定误差。滑模控制系统的稳定误差如图5所示，PID控制系统的稳定误差如图6所示。

图5 滑模控制下的跟踪环稳定误差Fig.5 Stability error of tracking loop under sliding mode control

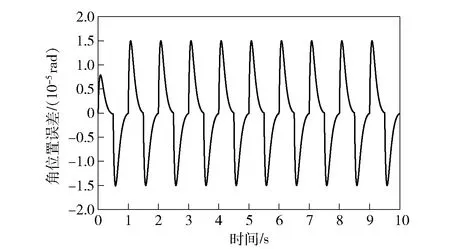
图6 PID控制下的跟踪环稳定误差Fig.6 Stability error of tracking loop under PID control

由图5和图6可见：滑模控制系统的误差的峰值1.54×10rad，标准差为6.88×10rad；PID控制系统的稳定误差的峰值为1.49×10rad，标准差7.88×10rad，可以看出滑模控制能更好地抑制稳定误差。

3.2.3 增大摩擦扰动后跟踪环稳定控制对比试验

系统在实际运行时，使用环境的不同，应用过程中的外界变化和系统本身变化，都会使系统的摩擦系数发生摄动，对摄动的抵御能力强能保证系统的稳定性。将摩擦扰动变为原来的两倍后比较 2种控制系统的位置误差，结果如图7和图8所示。

图7 增大摩擦扰动后滑模控制下的跟踪环稳定误差Fig.7 Tracking loop stability error under sliding mode control under increased friction disturbances

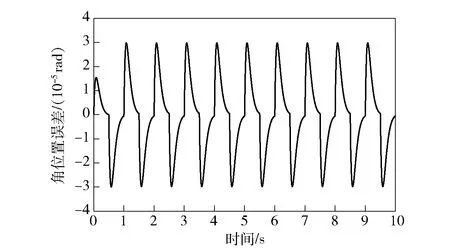
图8 增大摩擦扰动后PID控制下的跟踪环稳定误差Fig.8 Tracking loop stability error under PID control under increased friction disturbances

由图7和图8可知：此时滑模控制的误差峰值为2.61×10rad，标准差为8.09×10rad；PID控制系统的误差峰值为2.98×10rad，标准差为1.57×10rad；在摩擦扰动增大后PID控制系统的误差和标准差均随着摩擦扰动增大为原来的2倍，滑模控制的误差仅在摩擦力换向时造成的误差有了一定的增长，平稳运行时可以较好地适应摩擦力的变化，误差的标准差增长了17.59%，说明滑模控制对摩擦扰动有一定的自适应能力。