地球同步转移轨道数字式太阳敏感器视场局部修正*
2022-08-27叶立军刘付成宝音贺西
叶立军,刘付成,宝音贺西
(1.清华大学 航天航空学院·北京·100084;2.上海航天控制技术研究所·上海·201109;3.上海市空间智能控制技术重点实验室·上海·201109;4.上海航天技术研究院·上海·201109)
0 引 言
数字式太阳敏感器(本文简称数太)是一种经典的测量太阳方向矢量的敏感器,具备原理简单、功耗低、质量小、视场大、可靠性高等优点,在卫星上具有广泛的应用。虽然数太低测量噪声小,但系统误差大,因此需要对其进行修正后再使用。例如,在地球同步轨道(Geosynchronous Orbit, GEO)段,配合地球敏感器等其他单矢量姿态敏感器进行双矢量定姿,确定卫星三轴姿态;地球同步转移轨道(Geosynchronous Transfer Orbit, GTO)远地点点火段,可作为卫星对地指向控制期间的姿态敏感器;还可以将其安装于卫星巡航对日面附近,作为GTO巡航段对日控制期间的姿态敏感器。
对于某些GEO卫星,在其转移轨道段进行远地点点火时,为了提高卫星姿态控制指向精度,需细分为小步长控制技术(如控制周期约0.1s)。而小步长模式下,星载软件可能无法完成星敏数据采集及星敏姿态解算,或者远地点点火时姿态抖动剧烈可能引起星敏跟踪相对困难,因此在转移轨道远地点点火模式下,可能用到数太+地敏的三轴姿态确定模式。
受内外方位参数不准确等影响,数太测量往往存在较大的系统偏差,引起卫星姿态指向控制误差,导致燃料浪费,进而减少GEO卫星在轨工作寿命。对于一个总变轨燃料约2000kg的卫星,如果对应1°控制误差导致约40kg的燃料浪费,若节省这部分燃料,卫星会额外获得约1年位置保持所需速度增量,进而延长卫星使用寿命。因此,为了尽量节省转移轨道期间燃料,需在远地点点火前对数太系统误差进行修正。
GTO卫星轨道一般为近地点约200km,远地点约36000km的大椭圆轨道。由于近地点轨道高度过低,可能引起轨道快速衰减,一般在第一或第二个远地点就需要执行远地点点火,以抬高近地点轨道高度。因此,如何在卫星入轨后远地点点火前不到6h时间内,快速获得所需的数太校准的实测值和标称值是需要解决的问题。
本文以工程实用为目标,通过姿态路径规划,使太阳在数太视场内绕指定局部区域(局部区域是指数太视场内特定两维角度形成的相平面区域)的边缘行进,获取数太和对应的星敏数据作为修正样本,以星敏数据为基准,采用二元三次多项式模型修正数太两轴测量系统误差,最后在指定的局部视场内任找一条太阳运行路径,用于验证在该局部区域内数太测量系统误差的修正效果。
1 总体修正策略
数太视场局部修正的总体策略是,在巡航对日模式下卫星能源和星载计算资源充裕时,获得数太修正所需样本数据(包括星敏测量数据和数太测量数据),并对数太视场进行针对性的局部修正;当在远地点点火模式下计算机计算资源紧缺而无法使用星敏姿态确定时,采用视场局部修正后的数太,由姿态基准与地平仪联合姿态确定,可实现远地点点火期间卫星较高精度的指向控制,并尽可能节省转移轨道燃料消耗。
GEO卫星通常配置以整星姿态为基准的星敏感器,其精度一般可达0.01°,此外,星敏与数太之间热变形误差为0.01°量级,该误差比数太测量误差小1个数量级,因此可将星敏作为数太的标校基准。星敏视场与数太视场互不重叠,太阳在数太视场内运动,在此期间星敏必然不受太阳光干扰,可以正常工作,这是本文方法可行的基础。
在巡航对日模式下(第一次远地点点火前),卫星对能源需求少,抽出一段时间(如90min),让卫星姿态稍微偏离标称对日姿态,完成对数太局部视场修正所需数据采集,整个过程示意图如图1所示。

图1 姿态路径规划示意图Fig.1 Schematic diagram of attitude path planning
图1中,卫星在巡航对日模式下,太阳稳定在标号为“0”的初始标称姿态。通过依次设置目标姿态(通过设置不同的卫星俯仰和偏航两轴姿态偏置角实现),控制卫星依次通过编号为①→②→③→④→①的目标姿态,上述机动执行完毕后,返回标号为“0”的初始标称姿态。
这样太阳在数太视场内的投影会划过一个封闭曲线,且该封闭曲线形成的区域应完全包络远地点点火期间太阳在数太视场内的运行轨迹。尽量均匀地选取封闭曲线上的若干点(点的个数需大于二元次多项式修正算法参数的个数),每个点均同时包含星敏测量数据和数太测量数据,这些点就是数太修正的样本。
数太视场局部修正的主要步骤示意如图2所示。

图2 数太视场局部修正步骤Fig.2 Process of partial field of view calibration for DSS
图2中,各步骤相应描述如下:1)建立巡航对日坐标系,并基于星敏计算巡航对日三轴姿态;2)根据远地点太阳在数太视场中的运行路径,规划本次姿态机动路径,简单起见,可采用多边形来规划姿态机动路径(如图1中采用了四边形规划姿态机动路径),路径规划问题就转化为多边形定点两轴目标偏置姿态角计算问题;3)在巡航对日模式下,将几组目标偏置姿态分别按①→②→③→④→①的顺序依次上注,引导卫星按规划好的路径完成姿态机动;4)按等间距原则选取姿态机动路径上的若干采样点,得到同一时刻数太坐标系下太阳矢量(实测值)和基于星敏计算的太阳矢量(理论值);5)采用事先开发的数太修正程序,得到数太修正参数,并上注至星载计算机。
一般来说,每次远地点点火卫星在惯性空间的姿态指向变化很小,太阳在数太视场中的运行路径比较固定,且近似为直线。在选择数太修正视场时可充分兼顾所有远地点点火,地面获取样本数据后,采用二元多次多项式修正算法,可得到点火期间数太修正参数。
若点火策略有变(便如在计划外的非远地点点火),或预计下一次远地点点火时太阳在数太内的运行轨迹将超过设定的封闭区域,还可以根据需要再次采用本文方法,在点火前的巡航对日模式段重新进行数太视场局部修正。
2 二维曲面拟合修正算法
目前,针对探测器或镜头校准的文献有很多。胡小亮等和徐芳等采用多项式变形修正算法实现图像的全局高精度拟合;崔洪州等引入镜头畸变率的概念,将二维曲面拟合简化为一维曲线拟合,大大减少了待修正参数,实现镜头畸变修正,但该方法仅适用于径向畸变的探测器,不适用于多种系统误差相互耦合的探测器畸变修正;丁莹等采用标准网格模型求解包括径向、离心以及薄棱镜在内的多项镜头畸变系数,大大提高了修正精度,但该方法需要样本数均匀覆盖整个探测器,而本文背景下,系统使用数太前,可用于数太修正的时间短,无法获取整个数太探测器的样本数据,因此该方法不适用。
通过姿态规划机动,获取待修正区数太局部视场样本数据,每个样本数据包括数太实测值和理论值。采用二元多次多项式修正算法,可以确定理论值与实测值的对应关系,二元次多项式修正模型如下
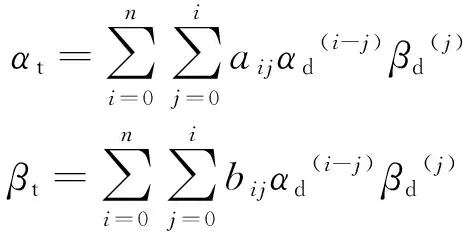
(1)
其中,(,)为基于星敏计算的数太两轴角度;(,)为数太测量的两轴角度;和为修正系数。
根据式(1),二元次多项式修正算法参数的个数为
=(+1)(+2)
(2)
根据式(2),与多项式次数呈平方关系,多项式次数越高,修正精度越高,但越大,计算量也相应越大。此外,本文采用数太视场局部修正方法,越大,样本点本身修正精度越高,但远离样本点的姿态解算精度会被迅速放大。远地点点火时,太阳处于样本点所围成的区域内部,对样本点本身修正精度太高,反而可能引起内部区域修正精度下降。因此,不能过大,一般基于星上计算资源和精度需求综合考虑选取。
3 修正样本获取
3.1 巡航对日姿态控制
巡航对日坐标系为参考坐标系,巡航对日坐标系到惯性系的3×3姿态转移矩阵表示为

(3)
其中,,,分别表示巡航对日坐标系三轴在J2000坐标系下的单位矢量;下标I代表惯性系,下标J代表巡航对日坐标系。
式(3)中各矢量表达式为
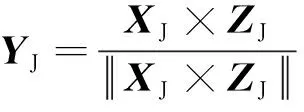
(4)
其中,=()为太阳矢量在J2000惯性坐标系下的单位矢量,下标S代表太阳;=(0 0 1)为J2000惯性坐标系轴。
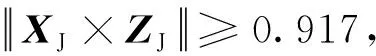
在巡航对日模式下,巡航对日坐标系到卫星本体坐标系的四元数为
=⊗⊗
(5)
其中,为巡航对日坐标系到惯性系的四元数,通过等价转换得到;为星敏测量得到的惯性系到星敏系的四元数;为星敏到卫星本体的安装四元数,下标T代表星敏坐标系,下标B代表卫星本体坐标系。
以为姿态基准,在控制作用下,使卫星三轴姿态保持在0附近,即实现基于星敏的巡航对日控制。
3.2 姿态机动路径规划
姿态机动路径规划,就是在巡航对日模式下,通过设置卫星三轴姿态偏置角,按时序依次驱动卫星姿态机动至相应规划点,则太阳会以预期路径附近在数太视场中运动。
在进行姿态路径规划时,需考虑以下几点:第一,这个规划的轨迹必须完全包围远地点点火时太阳在数太视场内的运行轨迹,其中远地点点火时太阳运动轨迹由地面仿真生成;第二,490N点火弧段比较短(一般约12°),可近似为直线,本文采用四点规划(凸四边形区域)法对该轨迹进行覆盖。
所谓的姿态机动路径规划,就是通过设计合适的目标姿态,使太阳落在数太视场内的指定区域。本文以卫星轴对日为例,旋转卫星轴(通过设置俯仰偏置角)和卫星轴(通过设置偏航偏置角),即可实现太阳在数太视场内的改变。对于某个待规划点,巡航对日轴在数太坐标系的矢量为

(6)
其中,为卫星本体系到数太坐标系的3×3姿态转移矩阵,下标D代表数太坐标系;为待规划点对应的俯仰偏置角;为待规划点对应的俯仰偏置角。
根据之前给出的规划点坐标和式(6),可解算出和。和也可视为目标姿态,采用巡航对日段姿态控制参数,以更新目标姿态后的为姿态基准,卫星三轴姿态收敛并保持到0附近的过程,即姿态按规划路径机动的过程。
3.3 数太修正用理论值计算
依次设置3.2节4个规划点对应的俯仰和偏航姿态偏置角,使卫星执行相应的姿态机动。地面通过遥测获取一系列采样点,包括:数太测量值(,),星敏测量四元数,以及太阳在惯性系下的单位矢量,可计算出基于星敏的数太修正用理论值(,)

(7)

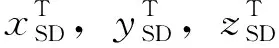
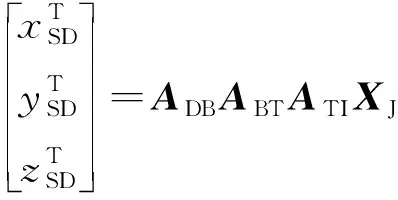
(8)
式中,是星敏坐标系到卫星本体坐标系的3×3姿态转移矩阵;是等价转换得到的J2000惯性系到星敏坐标系的3×3姿态转移矩阵。
4 仿真与分析
数太畸变误差包含了内外方位元素误差,其中外方位元素误差主要是安装误差;内方位元素误差包括径向畸变误差和切向畸变误差等。为了使修正前后效果更直观,设计数太最大误差约7°。
局部区域的选定与后续490N点火时的任务有关, GTO段490N远地点点火时长一般不超过2h,对应点火弧段一般不超过15°,而数太视场为±60°,490N点火弧长在数太视场内占比很小,其运动轨迹一般也可近似为一条直线。本文将修正的局部区域适当放大到数太对角线区域,一方面是为了突出修正的适用范围;另一方面为了增加姿态机动路径长度,证明在指定时间内可以完成姿态机动任务。
在姿态机动过程中,地面通过遥测获得一系列数太修正用样本数据,如表1所示。
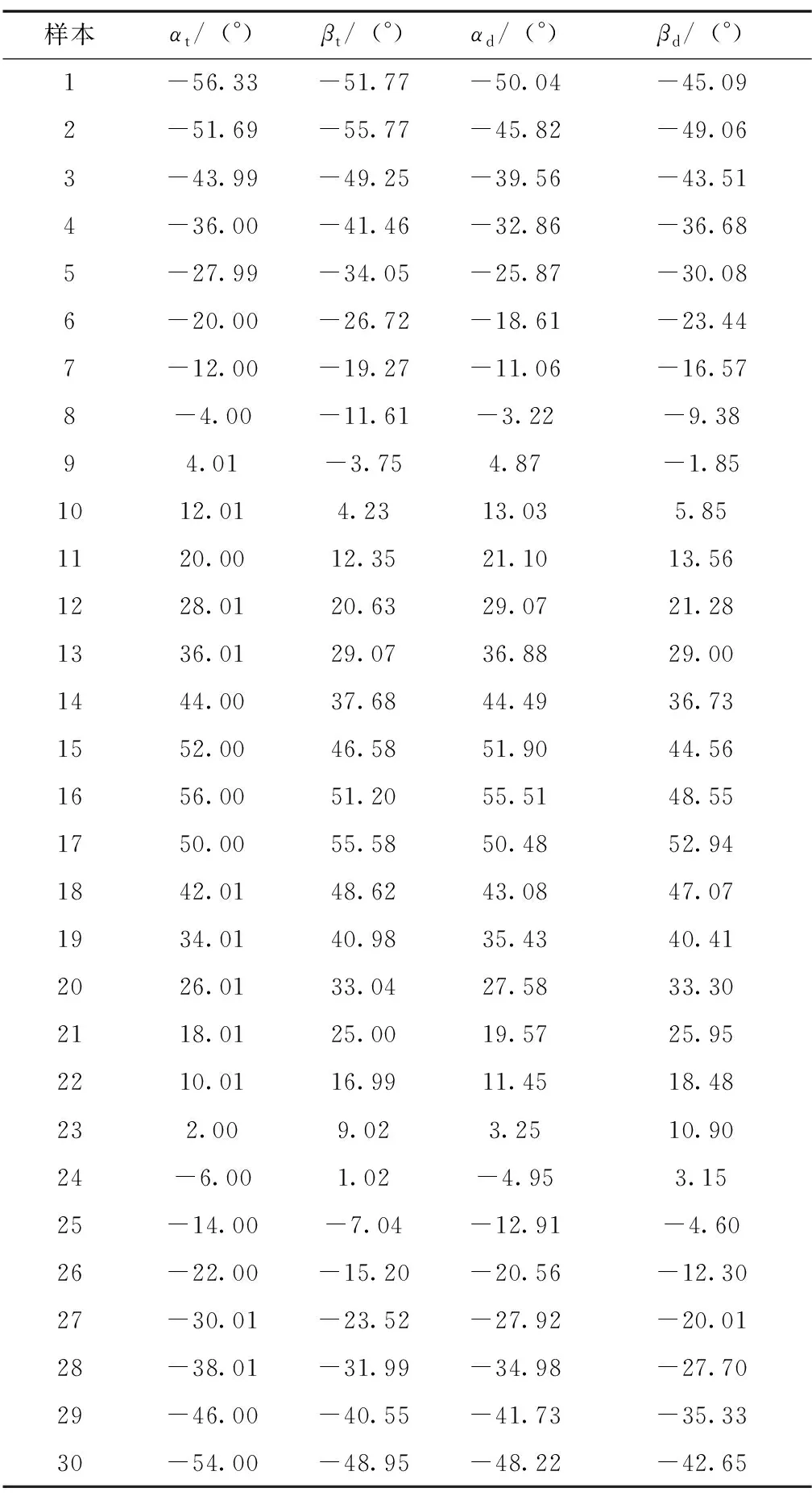
表1 数太修正用样本数据Tab.1 Sample data for calibration of DSS
在数太探测器视场内,这些样本点如图3所示。

图3 星敏感器测量四元数与卫星姿态角的变化Fig.3 Comparison of dark original color statistic distribution
图3中,理论(红色星号)代表基于星敏测量计算出的太阳在数太探测器坐标中的位置;测量(蓝色圆圈)代表数太测量太阳在数太探测器坐标中的位置。可以看出,由于数太径向畸变误差的原因,与理论太阳位置相比,数太实际测量太阳位置更加靠近数太视场中心。
基于式(1),采用最小二乘法,拟合得到二元三次多项式修正参数,如表2所示。
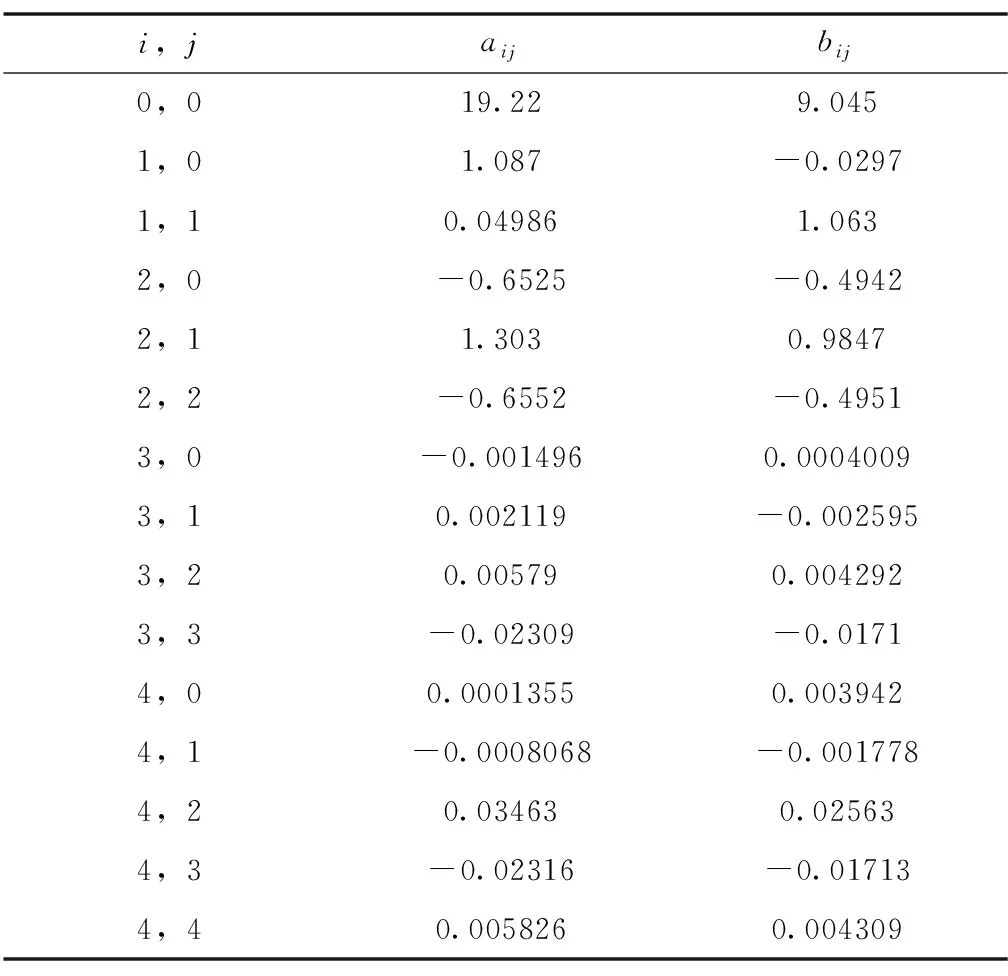
表2 多项式修正参数Tab.2 Parameters for polynomial correction
基于局部视场样本数据得到修正参数,计算数太全视场内修正误差,如图4所示。

图4 数太全视场修正误差二维曲面图Fig.4 Full field correction error surface diagram of DSS
由图4可以看出,经修正,在修正区域内误差较小,而修正区域外误差急剧变大,视场边缘处误差甚至达到850000°。也就是说,本文方法仅适用于数太视场局部修正。
为了验证局部区域的修正效果,除了控制卫星沿规划路径运行一圈,以验证路径上修正误差情况外,还在规划路径内部额外规划一条路径,用于验证局部区域内部修正后误差,修正效果如图5所示。

图5 星敏感器测量四元数与卫星姿态角的变化Fig.5 Comparison of dark original color statistic distribution
图5中,基准(红色实线)代表基于星敏测量计算出的太阳在数太探测器坐标系中的运行轨迹;修正前(蓝色实线)代表数太测量太阳在数太探测器坐标中的运行轨迹;修正后(黑色点虚线)代表经视场局部修正后,数太测量太阳在数太探测器坐标中的运行轨迹。可以看出,在局部区域以外,数太修正误差远大于修正前数太误差;但是在局部区域以内,数太修正误差则远小于修正前数太误差。因此,本文介绍的数太视场局部修正仅适用于当太阳在规划区内时的数太修正,一旦太阳运行轨迹处于规划区以外,应立即停止数太修正。
进一步分析数太修正前误差曲线,如图6所示。
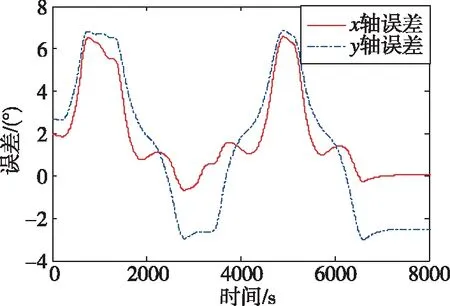
图6 修正前数太两轴姿态角测量误差Fig.6 The measurement error of two axis attitude angle for DSS before correction
图6中,轴误差(红色实线)代表数太修正前在数太轴姿态误差;轴误差(蓝色点虚线)代表数太修正前在数太轴姿态误差。可以看出,数太修正前两轴最大误差约7°。
数太修正后误差曲线,如图7所示。

图7 修正后数太两轴姿态角测量误差Fig.7 The measurement error of two axis attitude angle for DSS after correction
图7中,轴误差(红色实线)代表数太修正后在数太轴姿态误差;轴误差(蓝色点虚线)代表数太修正后在数太轴姿态误差。可以看出,数太修正前两轴最大误差约0.6°,且离规划边界越近,修正后误差越小。
经过修正前后数太测量误差对比,可以看出,修正后数太测量误差比修正前减小约10倍,精度提升明显。
5 结 论
本文讨论了GTO段远地点点火期间数太定姿条件,在GTO巡航段以星敏为姿态基准,采用姿态路径规划的方式获取数太局部视场样本数据并遥测下传,地面采用二维曲面对样本数据系统误差进行拟合。仿真证明,在490N点火期间,采用拟合后的数太测量误差减小了1个数量级。本文所提方法在工程应用中有以下几点需要注意。
1)在视场局部修正区域内,修正后的数太两轴姿态测量误差比修正前小1个数量级左右,但在局部修正区以外,修正后的数太两轴姿态测量误差则远大于修正前,因此,一旦太阳运行轨迹处于规划区以外,应立即停止数太修正;
2)远地点点火期间,太阳在卫星本体坐标系内运行轨迹固定,仅需针对其中一个数太进行规划即可,无需对每个数太都进行规划;
3)本文仅讨论了采用本方法可以有效减小数太在490N点火时局部视场的系统误差,但数太局部视场修正所需样本数据最优选取办法还有待研究;
4)采用姿态偏置实现太阳在数太视场中运动,此过程中,使太阳移动到目标点的三轴姿态偏置方法有无数种(卫星绕太阳矢量的轴是自由的),本文选取原则是姿态转动角不偏置,工程上还可根据实际情况添加对该轴的约束。
