思维导图法在高等数学教学中的实践研究

王 娜

（山西工商学院计算机信息工程学院，太原 030006）

高等数学课程作为一门工具性学科，是众多学科、知识的理论基石，在高校课程体系中占有重要的地位[1]。当下，对高等数学教学的研究已经非常成熟，基于这些研究许多学者也取得了良好的实践成果。尽管如此，一些学生对高等数学的学习积极性和主动性依然不高，解决问题的能力和逻辑思维能力有待提升，因此，探讨在高等数学教学中加入一种更有效的工具——思维导图来改变这一现状尤为重要[2]。

1 研究背景

思维导图作为一种先进的教学工具已经被国内外学者应用于多个领域。Russell Matthew L等[3]论述了思维导图在家庭会议中的效果；Sesanelvira ADIM等[4]借助思维导图对儿童食品安全行为进行了深刻分析。我国学者石向东[5]研 究了思维导图在思想政治课程教学中的应用；罗自强等[6]研究开展了思维导图在生理学教学中的应用并给出了一定的建议；李瑞兵[7]介绍了思维导图在高职数学教学中的实践。尽管思维导图在中小学以及高职教育教学中广泛应用，但在高等教育教学中的应用却较少。基于此，将思维导图引入高等数学教学中，具有一定的必要性和现实性。

1.1 思维导图的内涵

思维导图（The Mind Map），又称脑图、心智地图、脑力激荡图等，是将各级主题的关系与相互隶属的层级关系用图文形式有效表达的思维工具，也是一种将思考方式图示化的辅助工具[2]。

1.2 思维导图的绘制

放射性思维是人类大脑最自然的思考方式，它运用左右脑机能，借助阅读、思维及记忆规律，协助人们在科学与艺术、逻辑与想象之间平衡发展，从而开启人类大脑的无限潜能，思维导图的绘制是这一思考方式的再现。思维导图一般是用一个中央关键词或想法为中心，由此向外以辐射线发散各种关节点，每个关节点继续向外发散更多的关节点，每个关节点可以加入颜色以及不同的图形进行区分，呈现出放射性的立体结构。因此，思维导图由中心图、分支、关键词、线条、颜色和图形及符号语言六个要素构成[8]。其绘制步骤如下：首先，选定思维导图的中央关键词并以此为中心；其次，凝练中央关键词相互隶属的主题作为节点；再次，将节点划分出层级，按照层级进行排序；最后，用辐射线将中心与节点串联起来。根据上述步骤简单绘制的思维导图示意图，见图1。

图1 思维导图示意图

2 教学实践

2.1 引入思维导图的必要性

高等数学不仅为后续数学课程、专业基础课以及相关课程打下必要的数学基础，更为专业人才的培养起到服务性的作用。多年来，一些学者借助信息技术将“翻转课堂”“雨课堂”等教学模式应用于高等数学教学，开展不同形式的教学改革，如果将思维导图法也引入高等数学的教学中，效果可能会更加显著。

由于高等数学课程一般在大学一年级开设，学生正处于高中与大学的过渡期，初次接触高等数学知识，学习上会出现很多问题，比如内容繁杂、概念定理抽象、知识点难以理解等。另外，教师传统教学理念下开展的灌输式教学也影响了学生学习的积极性和自主性。为了解决这些问题，教师将思维导图法引入高等数学教学实践中，希望能够改善教学环境，促进学生学习兴趣和良好学风的形成。

2.2 思维导图法教学思路

教学团队以行动导向为理念，结合学生的基本情况进行有效分组，根据高等数学的内容整理出教学过程中的重点、难点，按照课前、课中、课后的教学过程安排学生制作、展示、优化思维导图，在实现教学一体化的同时，培养学生自主学习精神。具体实施思路见图2。

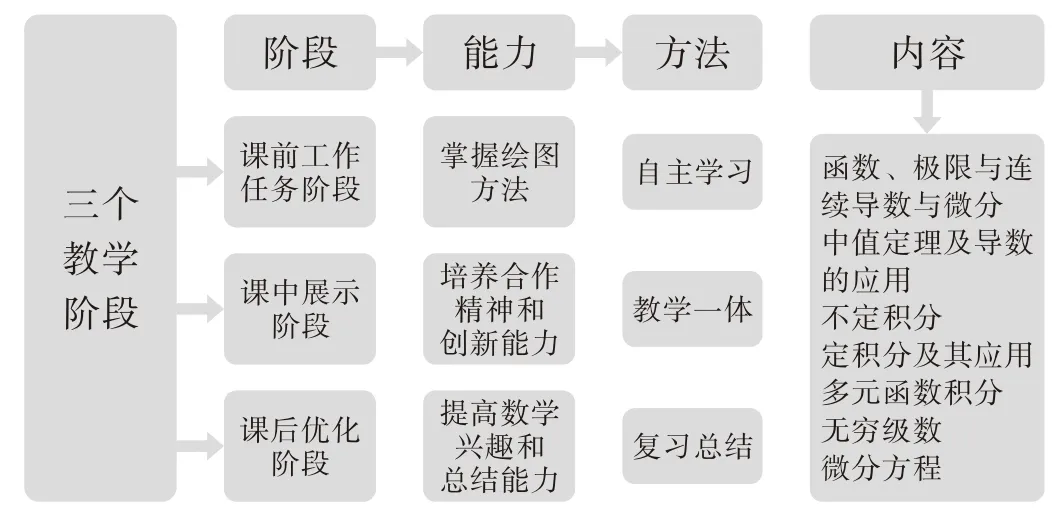
图2 思维导图法教学思路

3 教学原则

3.1 思维发展原则

高等数学教学的开展一定是基于学生当前思维水平的前提下，难易程度适宜大多数同学，因此教师在教学中要求学生使用思维导图时，根据学生的图式，设置情境或者问题引导学生主动思考、主动探索，通过任务驱动法使学生养成善于思考的学习习惯，增强学生思维发展[9]。

3.2 因材施教原则

由于地域教育的差异性，初入大学的学生具有不同的学习思维水平，因此，在实际教学过程中要考虑学生身心发展的差异性，要善于倾听学生的不同意见，发现学生的不同表现，尽可能创造条件实现差异性教学。尤其是在思维导图绘制过程中，学生会有自己的创意和想法，教师要善于接纳和鼓励，促进学生的全面发展[10]。

3.3 问题解决原则

高等数学教学过程中开展思维导图绘制的过程是将碎片知识点进行梳理的过程，也是将数学问题进行解决的过程，通过有效制作思维导图，学生将大量的知识点或者数学问题梳理、总结，进而提升学生问题解决的能力[11]。

3.4 教学相长原则

教学过程中，通过思维导图法的运用，教师借助学生的优秀思维导图进行教学，学生从教师的思维导图教学中获得清晰、条理的高等数学知识点结构图，使学生学习效果事半功倍。教师和学生在教学中共同成长、共同促进，形成良好的教学循环系统，营造和谐的师生关系[12]。

3.5 教学策略

3.5.1 示范-模仿教学策略 在高等数学教学过程中，思维导图法的应用不仅贯穿于高等数学课前、课中、课后三个阶段，而且适用于高等数学全部内容，因此，对学生制作思维导图的熟练度以及应用思维导图的灵活度都有一定的要求，但是，往往刚上大一的学生在此方面还是薄弱阶段，因此教师应当通过示范 -模仿教学策略帮助学生完成过渡[13]。

（1）动作定向——思维导图制作示范。教师需要向学生阐明思维导图的定义、制作软件、制作步骤以及其应用范畴，通过课前录制小视频或者课上演示的方法，教会学生思维导图制作的技能。

（2）参与性练习——学生参与思维导图制作。通过课下的时间，教师指导学生模仿练习制作思维导图的步骤，帮助学生尽快对所学习的步骤由不够精确逐渐走向熟练。

（3）技能迁移——学生应用思维导图。学生制作思维导图达到精炼后，可以将思维导图毫不费力地制作出来，此时教师可以随时设置授课内容、解题思路、复习总结的思维导图任务，学生将制作思维导图的过程内化到大脑中，间接提高了学生高等数学的学习效率。

例如，高等数学第一章《函数、极限、连续》中的极限这一节是后续知识的基础，教师引导学生提出“极限是什么？”“我们学什么？”“极限有什么用？”这三个问题，通过这三个问题进行梳理教和学的思路和内容，同时，给学生演示如何制作围绕这三个关键问题展开的思维导图节点，示范制作的思维导图见图3。通过教师的示范，让学生通过知识的学习在课下围绕“极限怎么学？”“怎么求？”“怎么用？”的关键词进行制作，学生制作的思维导图各具特色，教师通过章节复习课展示给予学生肯定和鼓励，同时，让大家取长补短，将知识点全面串联，提升学生高等数学学习质量。

图3 教师示范制作思维导图

3.5.2 支架式教学策略 支架式教学策略是根据苏联心理学家维果斯基的“最邻近发展区”这一理念发展而来，它主要是指为学习者创造分解的学习任务，提供出框架或者支架帮助其更好地学习[14]。教师在将思维导图引入高等数学教学时，需要了解学生的基本情况，切合把握学生“最邻近发展区”。

（1）搭建支架。思维导图法应用于高等数学教学中，需要教师围绕当下的学习主题，按照“最邻近发展区”的要求拆解知识点，将课堂的难点、重点作为思维导图制作的对象布置任务。

（2）独立探索。给予学生时间，让学生独立探索，自行分析概念或定理的条件、概念或定理的形成过程、概念或定理的注意事项等，通过不断地探索，学生用思维导图呈现出自己的探索结果，极大地促进了学生自学能力的提高，让学生真正成为了学习的主人，更具有使命感和成就感。

（3）协作学习。教师按照每8人的容量给学生分组，设置小组讨论任务，学生在讨论的过程中将原来不确定的问题进行明确，将容易混淆的概念进行区分，将复杂的解题方法和技巧排列组合，通过学生与学生之间思维的碰撞完成思维导图的制作，不仅能够节省教师上课纠错的教学时间成本，还能培养学生合作创新的精神。

高等数学第四章《不定积分》是积分学的开端。首先，教师在上课过程中，让学生明确不定积分和求导运算的互逆关系，复习求导数和求微分的基本公式，然后引导学生将求导和求微分进行逆运算，建立这一“最邻近发展区”；其次，教师布置独立思考“不定积分的计算方法”任务，分小组完成这一思维导图，经过同学们的探索和合作完成了具有自己代表性的作品，见图4。

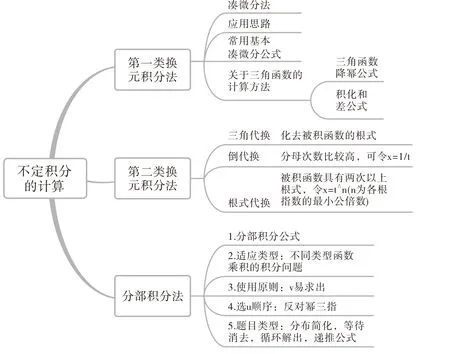
图4 学生自制思维导图

4 实证分析

山西工商学院开设高等数学课程的学院主要是建筑工程学院和计算机信息工程学院，涉及到7个专业12个班级，为了保证研究对象和统计数据来源的合理性，教学开展过程中选择同等职称水平的教师授课，尽量使用集体备课，保证授课进度和授课水平一致。教师将412名学生分成对照组和实验组，分别开展正常教学和思维导图教学，以学生一学期的期末总评成绩（期末成绩×60%+平时成绩×40%）为统计数据，借助EXCEL 2020软件进行统计分析，得到高等数学分数段统计表，见表1。

由表1可知，实验组各个班级大多数学生成绩位于区间[79,90]内，60分以下人数较少，而对照组中每个班级60分以下的同学很多，成绩呈现两极分化的情形，由分数段统计表可以看出经过思维导图法教学后学生的及格率明显提升。

表1 高等数学分数段统计

另外，借助SPSS Statistics 25软件，将实验组中共196位学生未进行思维导图之前的高数成绩和进行思维导图后的成绩进行成对样本T-检验后得到统计结果，见表2。

由表2可知，经过将思维导图引入高等数学教学中，学生的平均成绩由77.82分上升到了78.87分，标准差由13.379降低到了11.041，可见学生高等数学成绩整体波动降低，越来越趋于稳定。

表2 成对样本T-检验统计结果

通过实证分析，可以验证思维导图在高等数学教学中具有积极的意义。一方面提高了学生学习的兴趣和主动性，另一方面，提升了学生总结能力和解题能力，学生的成绩就是最好的证明。但是，由于学校开设高等数学的班级人数有限，统计数据的样本量不够多，有一定的局限性，尽管如此，根据教师与实验组的学生课下访谈和调查的反馈，学生对思维导图应用于高等数学教学中评价较好，不足之处在于教学时长有限，并不能将高等数学的全部内容制作思维导图，这也是激励青年教师在后续的教学实践中继续努力的方向。