基于后验噪声的贝叶斯鲁棒卡尔曼滤波器*
2022-08-26张楚元赵宗民王东峰
张楚元,曹 林,赵宗民,王东峰
(1.北京信息科技大学 a.光电测试技术及仪器教育部重点实验室;b.通信工程系,北京100101;2.北京川速微波科技有限公司,北京 100101)
0 引 言
最优滤波是信号处理的核心问题,想要设计出最优滤波器,就必须对统计模型有全面的了解[1]。然而,实际工程中不可能获得模型的全部信息。例如,很难得到某一场景下毫米波雷达观测噪声的准确信息,但可以设计一个鲁棒滤波器来处理这种不确定性。
卡尔曼滤波[2]是一种通过线性系统状态方程以及观测,对系统状态进行最优估计的算法。但它对噪声高度敏感[3],精确的噪声知识是影响估计精度的关键。最近,Dehghannasiri等人[4]利用贝叶斯创新过程和贝叶斯正交性原理,提出了一种本质上的贝叶斯鲁棒卡尔曼滤波器(Intrinsically Bayesian Robust Kalman Filter,IBRKF),它相对于成本函数和不确定噪声的先验分布是最优的,且该滤波器的递归方程与经典卡尔曼滤波器的递归方程相似。IBRKF定义了有效噪声统计量和有效卡尔曼增益的概念,并用它们来代替经典卡尔曼滤波器中对应的变量,以此改善性能。IBRKF是经典卡尔曼滤波器相对于不确定噪声的扩展版本。
尽管IBRKF的仿真实验证明了其性能的优越性,但其优越的性能仅建立在对先验知识的了解上,忽略了噪声信息可依托系统而传递这一关键因素。因此,如何有效地从观测中提取噪声信息是进一步提升估计精度的基石。
本文针对不确定观测噪声的问题,将IBRKF框架扩展到结合观测序列的后验版本,且所提算法的最终公式与经典卡尔曼滤波算法相似。该算法首先寻找与先验分布最为相似的提议分布,再为获得后验噪声分布的期望而设计了一种方法,借此使滤波算法不停地修正噪声参数,实现更精确的状态估计。通过对毫米波雷达实测数据的处理表明,该算法在应对不确定观测噪声时具有优异的性能。
1 贝叶斯滤波器
贝叶斯准则的含义是找到平均代价最小的滤波器。通常,在状态估计中,均方误差被用来评价滤波器性能的好坏,而优化滤波器的性能即最小化代价函数
C(xk,φ(yk))=E[(xk-φ(yk))T(xk-φ(yk))]。
(1)
因此,可将因果关系转化为根据最小化的代价函数找到一个最优的滤波器,即
(2)
式中:Ψ是所有可能的滤波器的类型。满足上式的滤波器即为最小均方差滤波器。
尽管IBRKF达到了先验意义上的最优,但先验噪声期望与实际噪声仍存在一定的误差,无法实现真正意义上的最优滤波。故本文重点考察后验噪声分布对成本函数的影响,通过提取观测中蕴含的有效噪声信息,进一步提升贝叶斯鲁棒滤波器的性能。
假设模型由未知参数ω=[ω1,ω2,…,ωl]控制,ω∈Ω,Ω为所有可能的参数的集合。此平均代价最小的贝叶斯鲁棒滤波器可表示为
(3)

2 贝叶斯鲁棒卡尔曼滤波器
假设观测噪声的协方差矩阵是未知的,由未知参数ω决定,即
(4)
并令π(ω)作为控制ω的先验分布,则状态空间模型可被参数化为
xk+1=Φkxk+Γkuk,
(5)
(6)
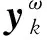
以式(3)的角度分析,满足此贝叶斯鲁棒滤波器定义的线性滤波函数为
(7)
式中:
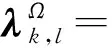
(8)
卡尔曼递归方程的推导基于以下的定理、定义、命题和引理:
定理1[4]:(贝叶斯正交原则)如果一个线性滤波器的权重函数满足式(8),则式(7)中得到的估计量被称为最优贝叶斯最小二乘估计,当且仅当

(9)

(10)

命题1[4]:根据贝叶斯创新过程,可得如下的方程:
(11)
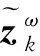
(12)
据此,可将式(7)改写为
(13)
然后,将式(13)代入式(12)可得

(14)
则状态更新方程可表示如下:
(15)
式中:
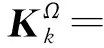
(16)
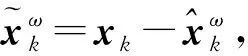

(17)
式中:Q=E[uk(uk)T]为过程噪声协方差矩阵。

3 有效噪声的提取
定理2:①如果x服从高斯分布,对x进行线性变换后,新的变量仍服从高斯分布。②如果高斯分布x、v统计独立,则它们的和仍服从高斯分布。

(18)
在获得不确定参数的似然函数后,利用Metropolis Hastings算法采样得到后验噪声的样本集,并将样本均值当作k时刻后验观测噪声的期望。其中,样本选择采用的是接受-拒绝准则。假设ω(j)为第j次迭代结束时所生成样本序列的最后一个样本,在j+1次迭代时,将从提议分布q(ωcand,ω(j))中抽取一个候选值ωcand,这个候选值通过计算接受率而被接受或者拒绝。接受率的表达式如下:
(19)


Fréchet距离的物理意义是空间中两条连续曲线变化趋势相似性的度量,而离散Fréchet距离则是将空间中的曲线看作由多个有序点构成的多边形,再通过匹配两条曲线的各个端点,寻找最长链接的最小值。
令空间中两条被多边形化的曲线为F:{c1,c2,…,cp}和G:{h1,h2,…,hq},L为两曲线逐点匹配所构成的链接序列,表示为
(cf1,hg1),(cf2,hg2),…(cfm,hgm)。
(20)
式中:f1=1,g1=1,fm=p,gm=q,且对于i=1,2,…,q,必须有fi+1=fi或fi+1=fi+1;gi同理,以此保证曲线中各端点的顺序关系。定义两曲线各匹配点的距离的最大值为
(21)
式中:d(·)表示两点间的欧氏距离。则F、G间的离散Fréchet距离可表示为[5]
ddF(F,G)=min{‖L‖|L为F、G间链接序列}。
(22)
由于文献[6]指出,当以离散Fréchet距离衡量两曲线的相似性且取到峰值点时,则其中一条曲线的某个峰值点只可能与另一条曲线对应的峰值点或其周围的几个峰值点相关,否则两曲线不可能相似。又因为概率密度函数体现了随机变量在某个确定点附近出现的概率,所以在寻找合适的提议分布时,可只取提议分布和先验分布波峰部分的点,使得链接序列至少含有一个峰值点,以此种方式压缩搜索空间,提升所寻提议分布的准确性。
基于提议分布与先验分布的离散Fréchet距离,可采用改进的随机游走算法寻找距离的最小值,并将距离最小时的提议分布作为最优解输出。采用改进后的算法是由于基础的随机游走算法依赖初始迭代点的设置,当经验不够可靠时容易使算法陷入局部最优。虽然增大迭代次数和初始步长可在一定程度上对这种问题进行改善,但这将造成时间花费的提升。因此,本文将离散Fréchet距离考虑为目标函数,寻找最优提议分布的过程如下:
Step1 按经验设置初始提议分布N(μ,θ(0)),定义初始步长ζ和控制精度ε,计算初始提议分布与先验分布的离散Fréchet距离D。
Step2 给定迭代次数N,并令当前迭代次数n=1。
Step3 若n θ(n)=θ(n-1)+ζ·min{θj},1≤j≤m。 (23) Step4 计算新提议分布N(μ,θ(n))与先验分布的离散Fréchet距离D′,若D′ Step5 若连续N次迭代都找不到更优的离散Fréchet距离,则认为最优解在以当前最优解为圆心、半径为步长ζ的圆内。此时,若ζ<ε,则终止算法;否则,令ζ=ζ/2,返回Step 2。 本文针对真实场景下的测量数据进行了实验分析,实验的对象是人。实验情况描述如下:在室内划定175 cm×450 cm的区域,并在实验区域的底部放置毫米波雷达。以雷达的位置为坐标原点(仅考虑二维空间的情况),利用雷达在没有任何目标的情况下对实验区域中的环境进行采样,并以此为基准滤除非目标点。数据采集时,一个人以近似匀速的运动方式在实验区域内按预定的轨迹走动,如图1所示。毫米波雷达安装位置如图2所示。在获得测量点后,对目标点进行聚类预处理,并以聚类中心为目标的观测位置。预处理结束后,利用三种不同的卡尔曼滤波器对这些位置数据进行滤波处理并分析误差。 图2 毫米波雷达安装位置 在滤波处理中,使用的滤波器分别为经典卡尔曼滤波器、IBRKF和本文所提的算法。根据所使用的雷达型号和多次测量的经验可知观测噪声的方差服从均匀分布。上述三种卡尔曼滤波器的滤波结果如图3所示,其中图3(a)代表本文所提出的算法,图3(b)代表IBR方法,图3(c)代表经典卡尔曼滤波算法。从图3可以明显看出,本文所提算法的滤波轨迹优于其他两种方法,更接近目标的真实轨迹。另外,经典卡尔曼滤波算法由于状态空间模型的不精确而导致的噪声积累会对滤波的稳定性产生影响,而IBRKF和本文所提算法都利用了有效信息来削弱这种影响,使得它们的鲁棒性比经典算法更强。 (a)本文所提算法 以目标估计位置与真实位置之间的位置误差(Position Error,PE)为算法评价标准之一,其计算公式如下: (24) 式中:xtrue、yture表示目标的真实坐标,xes、yes表示由滤波器滤波后目标的估计坐标。从图4可以看出,尽管所设计滤波器的PE在某些时刻超过了IBRKF和经典卡尔曼滤波器,但从整体上观察,本文所提算法PE曲线大部分都位于其他两种滤波器的下方,误差也相对集中。而通过计算三种滤波器的平均PE(分别为4.614 7 cm、8.147 0 cm和9.892 8 cm),也可看出本文所提算法整体上的估计位置与真实位置间的误差更小。 分别计算了三种算法的均方根误差(Root Mean Square Error,RMSE),对三种算法的性能进行直观地比较。从图5可以看出,本文所提算法的RMSE明显低于其他两种算法。另外,三种算法RMSE的平均值(Mean of RMSE,MMSE)也清晰地显示出它们滤波性能的优劣。其中,经典卡尔曼滤波器的MMSE为11.406 7 cm,IBRKF的MMSE为9.516 1 cm,本文所提算法的MMSE为5.184 8 cm。 图5 三种算法的RMSE 表1是不同迭代次数下,寻找最优提议分布和整体算法的时间花费情况。其中,ε=0.000 1,算法运行的平台是Matlab R2018b,处理器为1.40 GHz的Intel(R) Core(TM) i5-8257 CPU和8 GB RAM。根据实验数据可以看出,随着迭代次数增加,寻优耗时也将成倍增长,但最优解的变化不大。而由于寻优过程与滤波是串行的关系,且寻优过程在整体算法中只执行一次,因此迭代次数的增加并不会影响后续每一时刻的滤波时间。故在某些情况下,可通过控制迭代次数和适当增大控制精度来提升整体算法的实时性。 表1 不同迭代次数下的寻优耗时和算法总耗时 本文针对毫米波雷达测量时观测噪声不确定的问题,从观测中提取有效噪声信息,设计了一种新型的贝叶斯鲁棒卡尔曼滤波器,并提出了一种提议分布的自适应选取方法。实验证明了与经典和最新算法相比,所提算法在处理不确定观测噪声时性能突出。但目前仍存在一些问题,例如在面对非高斯噪声时,所提算法的性能会大幅降低,且设计时忽略了过程噪声的转移,原因是过程噪声与状态变量不独立,需要通过大量的数据分析来获得它们的相关系数,但此方法无法保证算法的准确性和实时性。下一步研究将把过程噪声加入该滤波框架,进一步提升所提滤波器的性能,并为计算后验噪声期望设计更有效、更便捷的方法。4 实验与性能分析
4.1 实验场景

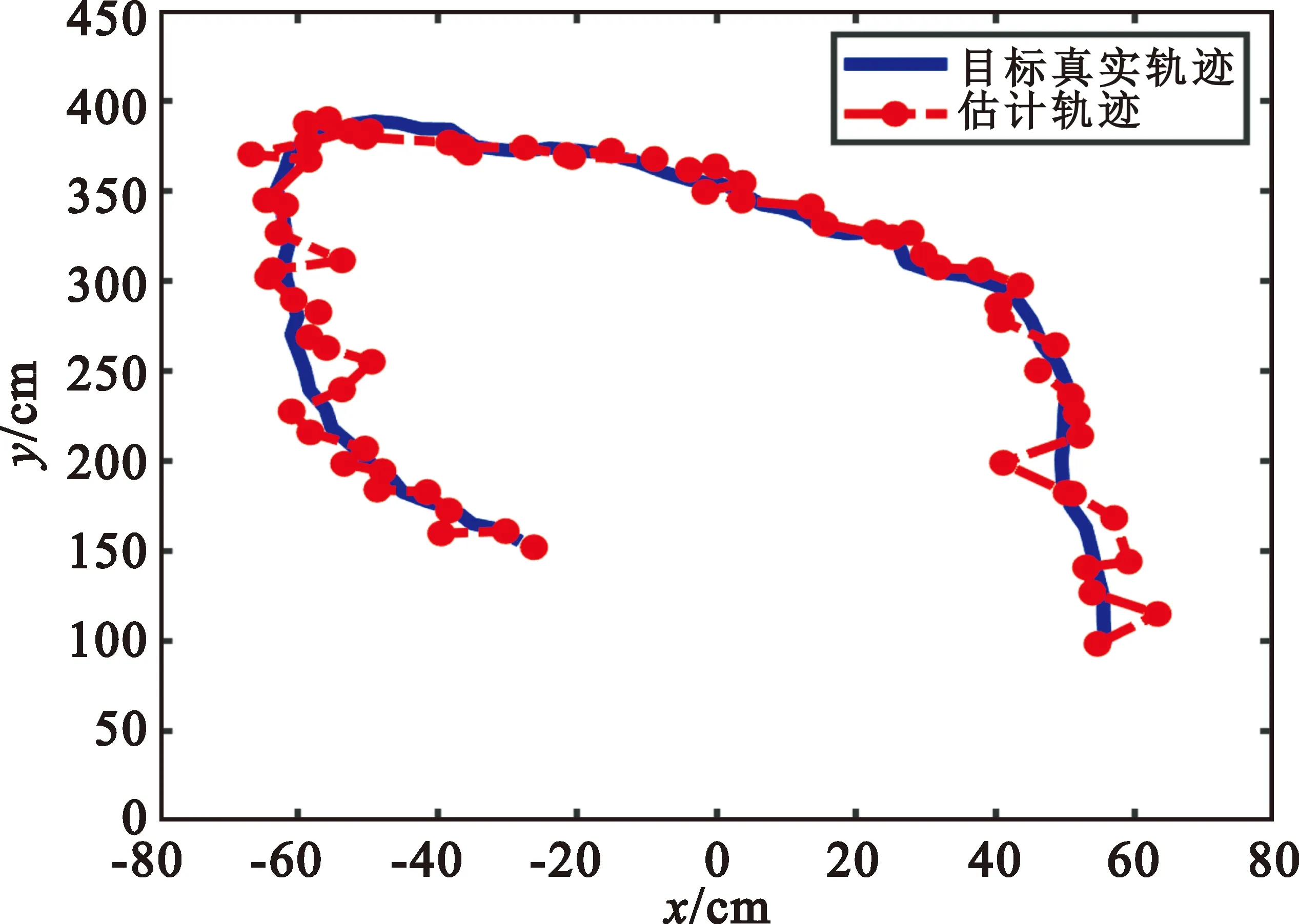
4.2 滤波轨迹
4.3 位置误差
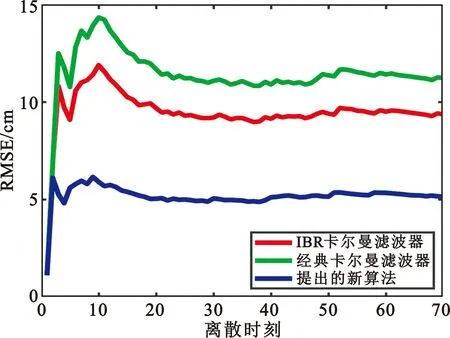
4.4 均方根误差
4.5 时间花费

5 结束语
