一种基于等价字符的不完整时间序列相似度算法*

黄 辰，张 蔚，吕 敏

(1.电子信息控制重点实验室，成都 610036；2.中国西南电子技术研究所，成都 610036)

0 引 言

时间序列的相似度算法是从时间序列中发现数据对象间相关程度和紧密程度的重要手段，是数据挖掘领域中重要的研究课题[1]。时间序列的相似度算法，即综合评定两个时间序列间关联程度的一种方法。两个时间序列特征越接近，它们的相似度越高。

相似度分析广泛运用于预处理[2]、信号处理[3]、聚类[4]、分类[5]、模式识别[6]、关联分析[7-8]、轨迹判断[9]、文本比较[10]等领域。在计算两组时间序列关系时，相似度度量所采用的数据特征和所选取的方法将直接影响数据计算效果。因此，根据数据特点选取相适应的相似度度量方法，对于提升相似度计算的准确性而言具有重要意义。目前，典型的相似度算法有基于最长公共子序列(Longest Common Subsequence，LCS)、基于贪婪字符串匹配(Greedy String Tiling，GST)[11-12]算法等。LCS和GST算法不要求待比较序列长度相等，且能处理具有少量强噪声的序列[9]。

文献[8]针对不等长序列的关联问题，提出了基于滑动窗口的最优匹配增权法，并验证了算法对不等长序列数据关联的有效性。文献[13]提出了基于涨落模式(Frequent Pattern，FP)的时间序列相似性度量研究方法，能有效支持识别多种相似性形变，以FP保存原序列的趋势变化信息，利用LCS算法计算涨落模式的相似度。

现有的相似度算法均在一定程度上解决了数据的相似度计算问题，但对于不完整时间序列而言并没有采取针对性的解决思路，因此并未达到理想效果。本文在充分研究现有算法的基础上，针对不完整时间序列的相似度计算问题，利用差分变换、量化处理、符号化处理、等价字符变换以及LCS、GST算法思想，提出了适用于不完整时间序列相似度计算的改进算法，并与典型的LCS、GST相似度算法进行了对比分析。

1 典型相似度算法介绍

1.1 LCS算法

LCS算法是将两组时间序列分别删去0个或多个字符，但不改变剩余序列顺序后得到最长的相同子序列。

设X1、X2为给定的两组序列，m、n分别为X1和X2的长度，LLCS为两组序列最长公共子序列长度，则LCS相似度计算公式为

(1)

1.2 GST算法

GST算法对两组时间序列进行贪婪式搜索，以找出尽可能多的匹配子序列，并求出最大公共子序列长度LGST。

用GST算法计算相似度公式为

(2)

式中：M、N分别代表匹配子序列在X1、X2中的起始及结束位置，Len代表匹配长度，titles代表所有匹配长度全集。

2 改进相似度算法原理

准确获取不完整时间序列间的最长公共子序列长度，是完成相似度计算的重要工作。对时间序列进行参数变换和符号化处理，计算并建立等价字符表，在此基础上滑窗搜索不完整序列间的相似部分，能更准确地计算出不完整序列间的最长公共子序列长度，并基于改进后的相似度公式计算出相似度值。

2.1 参数变换和符号化处理

通过参数变换和符号化处理将原始时间序列的比较转换为字符串之间的比较，以降低输入数据的信息量，便于后续理解和计算，其步骤如下：

Step2 将上述时间序列进行一阶差分变换后作为一维输入参数序列。经参数变换后的一维输入参数序列可表示为

Step3 采用层次凝聚聚类(Hierarchical Agglomerative Clustering，HAC)方法对上述输入参数序列进行非均匀矢量量化，量化完成后对所有量化值依次打上符号标签(为计算方便取数字形式)即为符号化序列。

设有如下两个时间序列：完整时间序列X1=(0,132,265,397,626,758,891,1 023)和不完整时间序列X2=(0,132,397,626,758,891,1 023)。

时间序列经一阶差分变换后分别为DX1=(132,133,132,229,132,133,132)、DX2=(132,265,229,132,133,132)。令距离阈值ε=1，按上述方法处理后得到符号化序列LX1=(1,1,1,2,1,1,1)；LX2=(1,3,2,1,1,1)。其中，符号值c1=1,c2=2,c3=3。参数变换后的聚类及符号化如图1所示。

图1 聚类及符号化示例图

2.2 等价字符表映射

在时间序列的采样过程中，由于各种原因可能会有数据缺失的情况发生，为此本文提出了一种等价字符表映射技术以解决最长公共子序列提取不准确的问题。

基于上述符号化序列建立时间序列的等价字符表。

定义1 设s为差值级数，k为时间序列连续缺失数据的实际个数，kmax为最大连续缺失数据的个数，m、n分别是两组时间序列的长度，在符号化序列的时间特征参数满足如下条件时建立等价字符表：

(3)

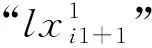
表1 s级等价字符表

等价字符表创建流程如图2所示。

图2 等价字符表创建流程图

令kmax=3，由图2流程及公式(3)可得到，2.1节例子创建的2级等价字符表如表2所示。

表2 2级等价字符表

2.3 动态滑窗搜索

结合等价字符表，采用动态滑窗的方式搜索匹配子序列。基本思路是选择其中一个序列为基准，对另一个序列进行滑窗搜索。

动态滑窗是指搜索窗口的大小和位置在匹配计算的过程中是随时间变化的。本文采用的动态滑窗在每一次比较时，窗口起始位置由向后移动一个序列单元，结束位置为序列末尾。动态滑动搜索窗口如图3所示。

图3 动态滑动搜索窗口

(2)字符比较判断准则

两序列字符搜索时的比较判断准则为，若两序列待比较字符相同或属于等价字符，则两序列待比较字符位置分别向后移动一个序列单元重复上述比较；若不相同且不属于等价字符，则只将待比较序列字符位置往后移动一个单元，按照上述方法继续比较，直至搜索到序列结束位置时输出匹配子序列。

2.4 融合GST思想的LCS改进算法

(1)最长公共子序列长度计算

在上述符号化处理、等价字符映射的基础上，综合考虑LCS、GST算法思想，进一步提出一种融合GST思想的LCS改进算法，滑窗搜索并提取所有非重复的匹配子序列，通过判断多次搜索得到的匹配子序列累计长度计算最长公共子序列长度。具体步骤如下：

Step1 使用上述动态滑窗及字符比较判断准则对两符号化序列开展搜索，搜索到序列末尾提取一次匹配子序列，对已提取的匹配子序列对应字符打上已使用标记，长度分别记为LM1、LM2。

Step2 重复Step 1，对未标记数据进行搜索，提取匹配子序列，得到匹配子序列累计长度，分别记为ALen1、ALen2，此时

(4)

式中：t为搜索次数计数，T为当前最大搜索次数。

Step3 每搜索完一次后，对所有输出的匹配子序列累计长度进行判断，当满足下式则提前停止后继搜索：

min(ALen1+1,ALen2+1)=min(m,n)。

(5)

其中累计长度分别加1是对应回差分前原始时间序列长度。

Step4 当满足搜索提前结束条件或提取完所有匹配子序列时结束搜索，计算最长公共子序列长度。

令LIGST(X1,X2)为改进算法的最长公共子序列长度，所有搜索结束则有

LIGST(X1,X2)=min(ALen1,ALen2)+1。

(6)

(2)相似度计算

由公式(1)、(4)、(6)可得，相似度计算公式为

(7)

根据公式(2)可知，

(8)

(9)

采用上述方式，2.1节例子的符号化数据搜索一次得到匹配子序列为(1,1,1,2,1,1,1)、(1,3,2,1,1,1)，匹配子序列累计长度分别为7、6。对其进行判断，满足公式(5)，因此停止后继搜索，此时根据公式(6)、(7)求得最长公共子序列长度为7，两序列相似度为0.933。

根据上述计算流程推导出如下定理成立：

定理1 令Sim1、Sim2和Sim3分别为时间序列X1和X2按LCS、GST和本文改进算法定义的相似度，则有Sim3≥Sim2≥Sim1。

证明：由LCS、GST和本文改进算法定义的最长公共子序列长度分别为LLCS、LGST、LIGST，由LCS和GST算法定义可知，

LLCS=match(M,N,LenLCS)∈titles，

(10)

则有

(11)

即LLCS≤LGST。

由本文改进算法定义，如果两序列满足等价字符条件，则等价字符对应的序列长度加入到最长公共子序列长度的计算中，因此有min(LM1,LM2)≥LenLCS，进一步得到

(12)

结合公式(2)、(7)～(9)可得

LIGST≥LGST≥LLCS。

(13)

由此可推出如下结论成立：

(14)

基于以上不等式，由相似度定义可推出Sim3≥Sim2≥Sim1。

3 实验与分析

3.1 等长随机漏脉冲对比实验

选取脉冲重复周期(Pulse Repetition Interval，PRI)类型为参差的样本序列进行等长随机漏脉冲相似度算法对比实验。将序列的TOA归一化到0起始，序列TOA参数为X=(0,50.3,117.4,175.9,245.9,296.2,363.3,421.8,491.8,542.1,609.2,667.7,737.7,788,855.1,913.6)，最大连续缺失个数kmax取3，按照漏脉冲数0、1、2、3的条件随机生成1 000组待测数据，分别利用LCS、GST、本文算法分析等长漏脉冲序列之间的相似度分布情况，结果如图4所示。

(a)漏脉冲数为0

由图4(a)可见，当序列为完整序列时，三种算法相似度计算值相等，而当序列为不完整序列时，随着漏脉冲数量的增加，不完整程度随之升高，相似度计算值总体会有所下降。通过分析图4(b)～(d)相似度分布情况可知，本文算法的相似度更高。

设图4中相似度精度取0.01，i=1,2,…,100，simi为第i个相似度值，numi为simi对应的统计次数，利用加权平均法可计算出相似度在多组统计中的算术平均数。加权平均相似度计算公式为

(15)

式中：simi=0.01×i；sum为总的测试次数，在本实验中sum为1 000。

将图4中的相似度分布进行加权平均计算，结果如表3所示，可见，本文算法相比典型算法有10%以上的性能提升。

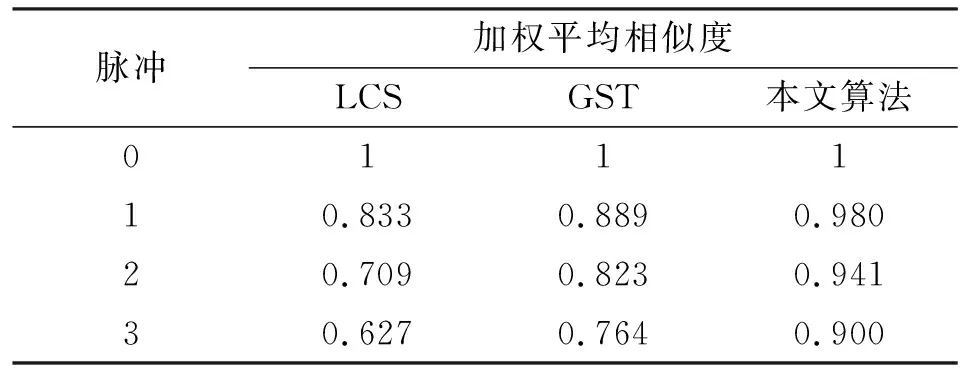
表3 漏脉冲为0～3条件下的加权相似度对比表

进一步地，选取4种典型PRI类型(A、B、C、D分别代表组变、参差、复合和滑变)的脉冲时间序列进行等长随机漏脉冲相似度算法对比实验，归一化后的序列TOA参数如表4所示。

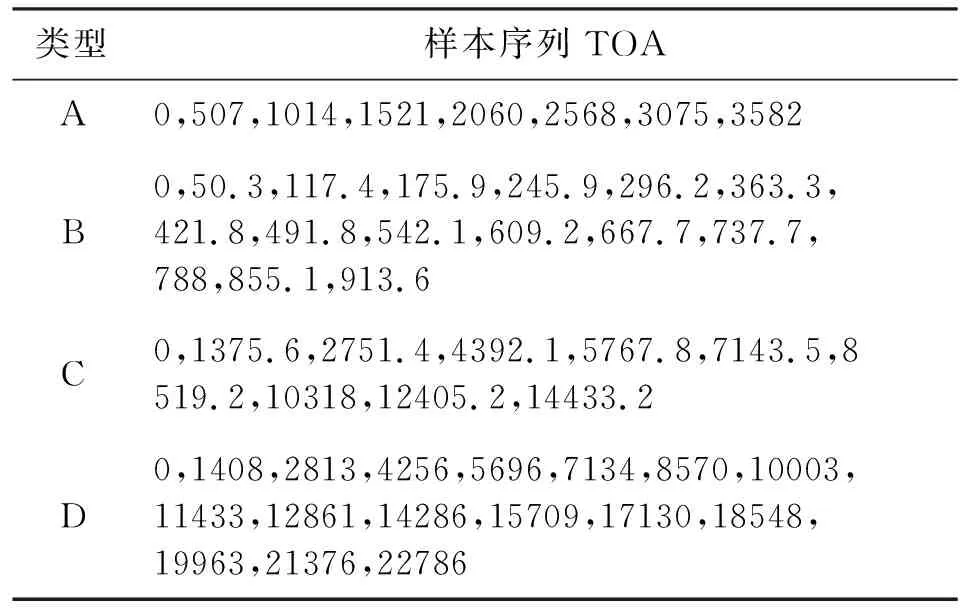
表4 4种PRI类型的时间序列

根据以上的测试方法，分别比较4种类型数据加权相似度随序列漏脉冲数量的变化情况，如图5所示。

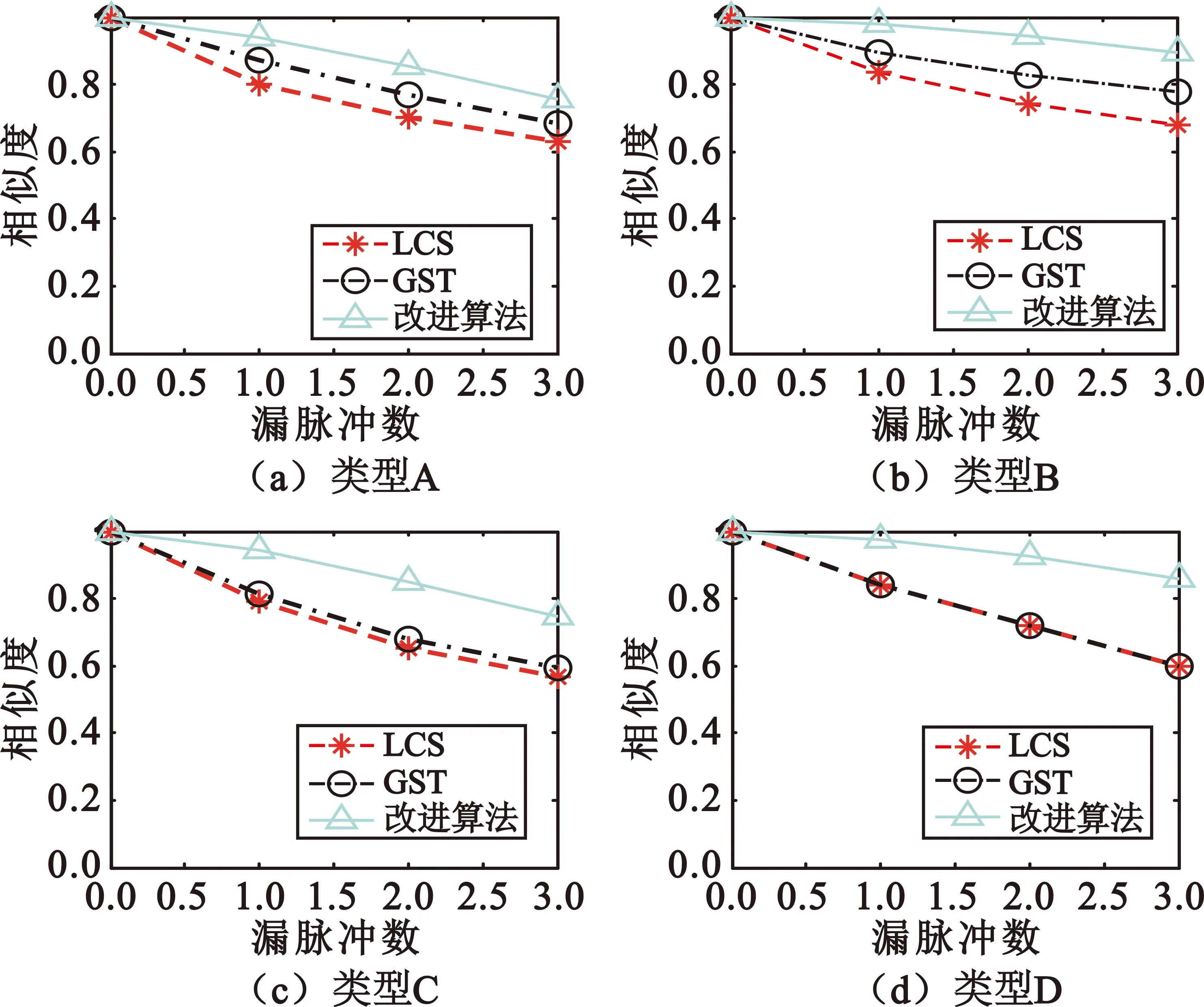
图5 4种数据类型的相似度对比图

可见，对于不同类型的测试数据，取相同长度的完整脉冲序列，随着漏脉冲数量从1增加至3，LCS、 GST方法计算出的相似度下降相对明显，本文算法的加权平均相似度高于其余两类算法。

3.2 非等长随机漏脉冲对比实验

选取4种不同PRI类型共8对时间序列进行非等长随机漏脉冲对比实验，序列TOA参数如表5所示。

脉冲时间序列经差分变换、量化处理及符号化处理后的结果如图6所示。

图6 不同脉冲时间序列符号化值对比图

表5 不同类型脉冲时间序列

利用本文方法计算上述序列对的相似度，与LCS、GST算法进行对比，结果如表6所示。

表6 各组脉冲时间序列相似度计算结果

不同类型脉冲时间序列相似度结果如图7所示。

图7 不同算法相似度结果对比图

以上总的相似度对比结果表明，在时间序列存在数据缺失情况时，利用本文方法计算得到的相似度高于LCS和GST算法，针对存在数据缺失的时间序列具有更好的效果。

4 结束语

本文研究了一种基于等价字符的不完整时间序列相似度算法，通过挖掘时间序列之间的内在规律提高一定数据缺失情况下的时间序列相似度计算准确性，在等长漏脉冲条件下，当脉冲缺失1～3个时，相比LCS、GST算法，本文算法的相似度计算结果有10%以上的提高。而非等长脉冲缺失对比分析表明，本文算法能有效提高对比序列的相似度结果。

虽然基于等价字符的方法能在序列不完整情况下能得到更接近于完整序列情况下的相似度计算结果，但漏脉冲数量会直接影响计算结果的可靠程度。因此，下一步工作可根据序列的不完整程度，研究相似度结果的置信度评估方法。