一种雷达导引头天线罩误差数字补偿方法*

杨胜华

(中国西南电子技术研究所，成都 610036)

0 引 言

弹载雷达导引头的天线罩既对雷达天线起保护作用,又要允许对雷达天线发射或接收的电磁波最大化穿透。天线罩一般安装在导弹的头部，是满足导弹弹体气动外形的重要组成部分，也是制导系统跟踪回路的组成部分。天线罩承载了透射雷达电磁波的作用，但不可避免对雷达电磁波有反射、折射和衰减等的传播影响，最终体现在对雷达天线瞄准线引入误差，这种误差耦合到导引头跟踪回路中，对制导性能造成很大影响[1-2]。

为了降低天线罩误差对制导性能的影响，常采用硬件和软件补偿法。边打磨边测量方法[3-4]，打磨和测量需要反复迭代，不能降低天线罩在使用过程中引入的误差。电子标定法或寻零法测得天线罩误差，利用等电平评价计算方法降低误差[5]。此方法用于测试天线罩的性能，未能完全反应误差，用电平评价计算方法只能减小部分误差。周荻等[7]所提方法的前提条件是天线罩误差是随机白噪声，无系统误差，仅适用于球形罩。宗睿等[8]所提方法对象是平台式导引头，罩误差斜率与电缆力矩、电机反电势一起作为随机量，结合制导回路进行滤波估算。曹旭东等[9]所提方法在回路内直接进行角度补偿，其缺点是在回路中直接引入误差补偿量，而补偿量又与方位、俯仰的角度相关，造成方位俯仰两回路耦合。

本文利用雷达单脉冲跟踪技术，提出用雷达导引头跟踪静止模拟目标的方法获取天线罩误差特性，导引头与天线罩的几何关系基本与装弹状态一致，对其中的安装误差和天线在罩内扫描状态下反射、折射和信道通道间不一致等引入的误差进行测量，然后在回路外进行数字补偿，对回路本身不产生影响，能更全面、更安全地减小天线罩引入的误差。

1 天线罩对波束角度和视线角速率的影响

1.1 天线罩对波束角度的影响

由于天线罩影响，弹目视线将偏离实际弹目视线，偏离角度为天线罩引起的视线角误差，计算公式如下：

σ=q-θm-φ-e。

(1)

式中：σ是天线罩引起的视线误差，q是视线角，θm是弹体姿态角，φ是雷达导引头波束中心线偏离弹体轴线的角度，e是波束中的失调角。当导引头波束角度为φ时，在天线罩外的实际波束中心不是φ，而是带有误差σ。误差σ是雷达工作频率f、导引头方位角θAz和俯仰角θEl的三元函数，即

σ=ErrData(f,θAz,θEl)。

1.2 天线罩对视线角速率的影响

根据图1的角度定义，带罩后雷达测得视线角为qm=q+σ,误差σ包含方位误差σAz和俯仰误差σEl。

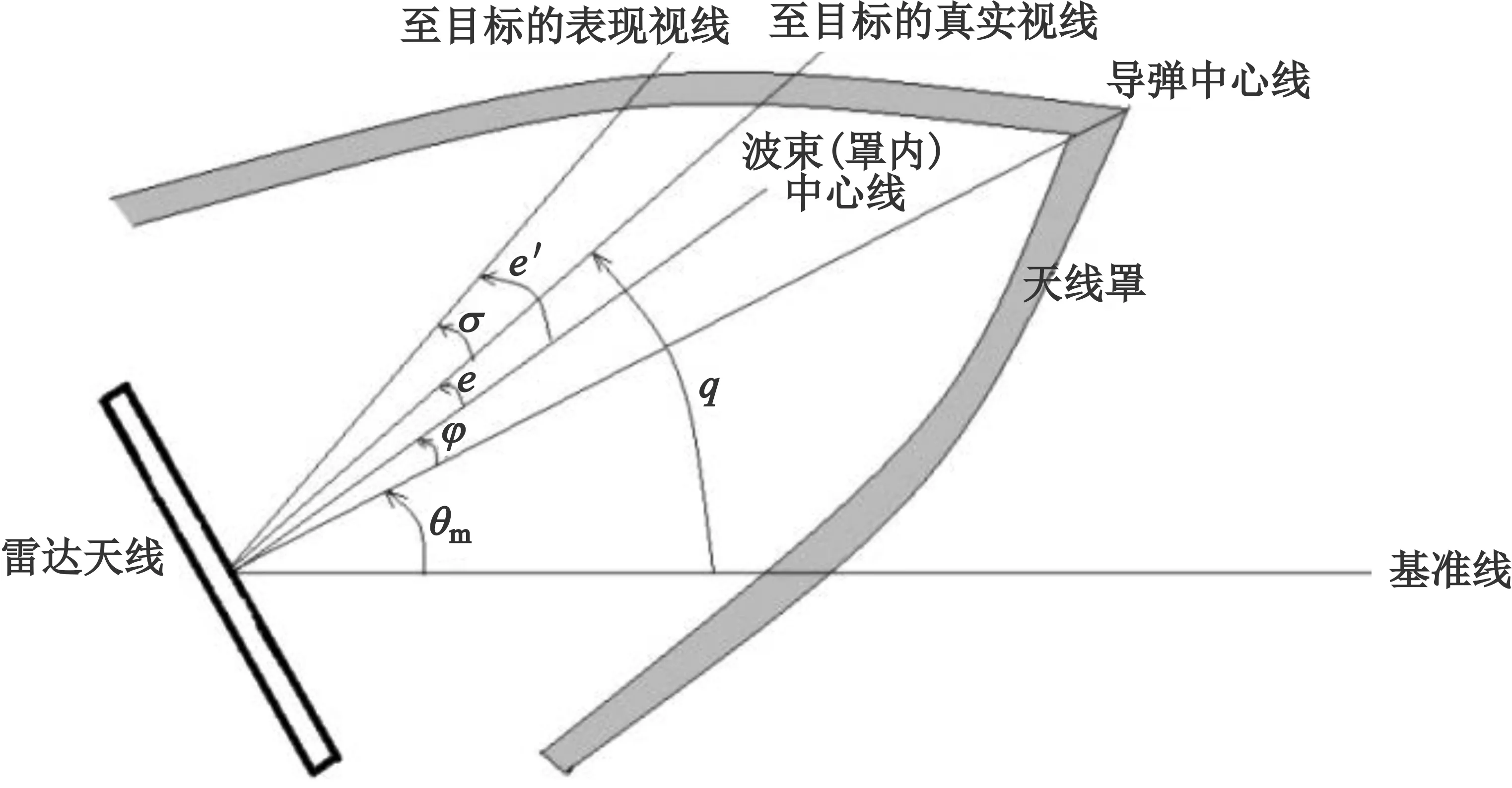
图1 天线罩对波束角度影响

(2)

2 角度和角速率测量方法

若雷达坐标系和弹体坐标系重合，在相控阵雷达中，雷达波控角度为波束中心在弹体系下的角度。

视线角速率按图2所示的角跟踪回路得到。其中，q(s)是视线角；MeasureAngle是单脉冲测角输出的目标偏离波束中心的角度值，归一化后为1；K为增益，一般K=10左右；BeamContr是波控单元，归一化后为1；1/s是积分环节；u(s)是视线角速率输出值。

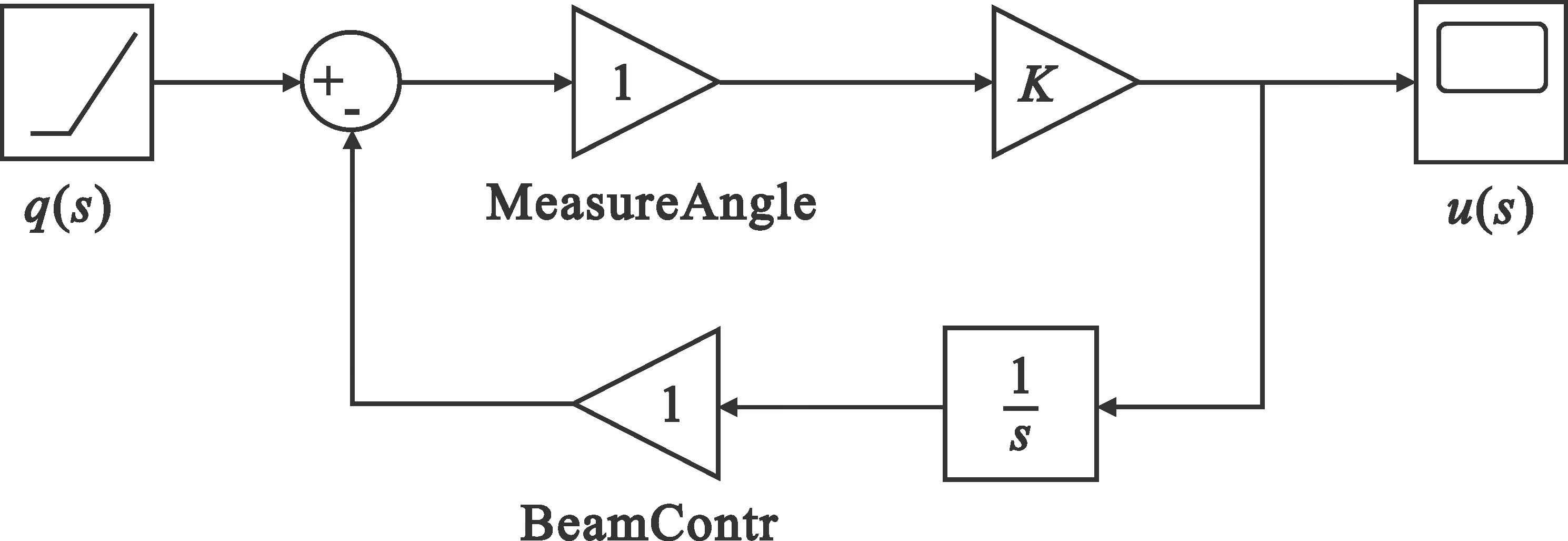
图2 视线角速率测量的简化原理图

根据自动控制原理可知，

(3)

3 天线罩误差测量方法

为了降低天线罩误差对角速率的影响，需要测量天线罩误差。天线罩误差测量原理如图3所示，其测试系统主要由目标模拟器、高精度二维转台、一维高精度滑轨、转台控制器、滑轨控制器、供电电源、安装工装架和相关控制软件组成。在微波暗室测量，暗室的尺寸必须满足天线远场条件，利用目标模拟器模拟雷达静止目标，雷达导引头用单脉冲跟踪技术对目标进行稳定跟踪测角，其得到的角度为波束中心角。控制转台按“走一步，测一次”的方法，覆盖导引头测量区域，记录在相同转台角度下带天线罩角度和不带天线罩的角度测量值，用雷达导引头的带罩角度减去不带罩角度，其差便是天线罩瞄准线误差，经处理后得到方位和俯仰两维天线罩误差表。

图3 天线罩误差测量原理框图

4 数字补偿算法

数字补偿分为角度补偿和角速率补偿，角度补偿包括指向补偿和测角补偿。

4.1 波束指向与测角补偿

指向补偿需要波束在无罩条件下指向空间某角度，加上罩误差得到带罩后的实际波控角度。测角补偿是雷达导引头在带罩条件下测得的目标空间角度，减去罩误差求取无罩下的实际目标空间角度。角度补偿值为实测天线罩误差值。工程中难以测得任意角度下的误差值，只能按一定间隔测量离散的误差值。由测量的误差值生成角度指向误差表和角度测量误差表，假定误差在小范围内是线性变化的，然后通过二维线性插值方法获取任意空间角度近似误差值。

如图4所示，二维线性插值算法根据所求角度点M的角度坐标(x,y)，查天线罩方位误差表得到其紧邻周围M11(x1,y1)、M12(x1,y2)、M21(x2,y1)、M22(x2,y2)4个点的坐标，其中x2>x>x1，y2>x>y1。M11表示方位角为x1，俯仰角为y1条件下，罩引起的方位误差为M11；同理M12、M21和M22为其对应方位/俯仰角条件下的罩引起的方位误差。按式(4)、(5)和(6)计算，得到点M的方位误差Mxy。

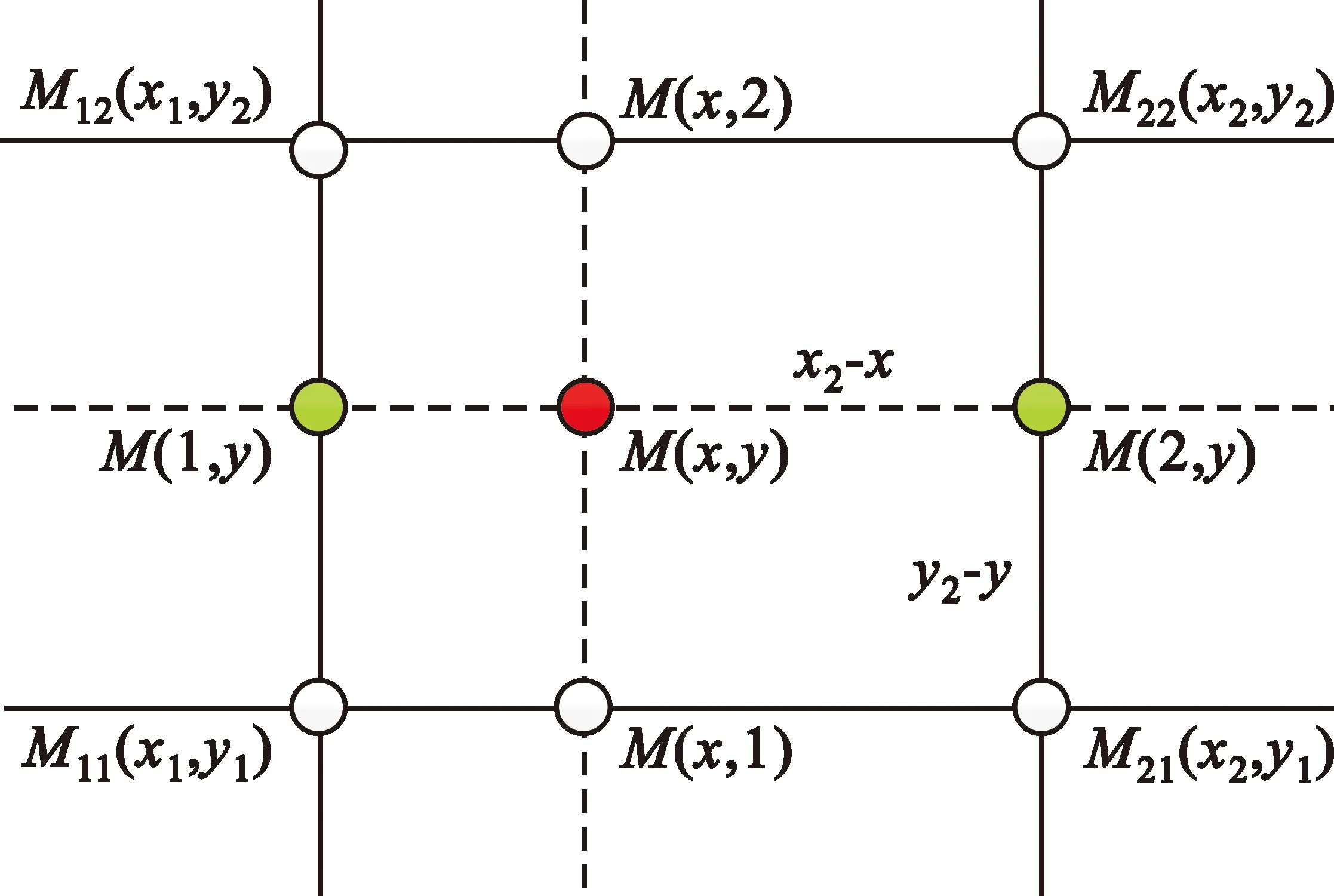
图4 线性插值算法

(4)

(5)

(6)

4.2 角速率测量值补偿

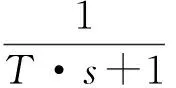
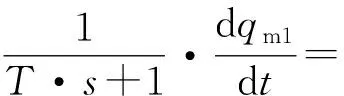
(7)

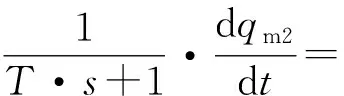
(8)

由式(7)和式(8)整理得

(9)

(10)

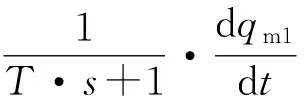
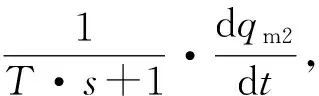
(11)

(12)

式(11)中M(1,y)和M(2,y)分别与式(4)和式(5)中的M(1,y) 和M(2,y)相同。式(12)中，

(13)

(14)

(15)

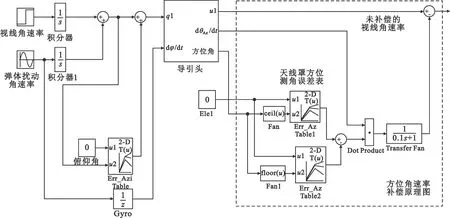
图5 角速率补偿原理图

5 仿真和试验验证

5.1 测量得到的天线罩误差特性

通过上述天线罩误差测量方法测得真实天线罩的误差特性，从图6中某频点天线罩方位误差特性可知，最大误差出现在方位角7°附近，约0.6°；从图7天线罩俯仰误差特性图可知，最大误差出现在俯仰角7°附近，约0.6°。

图6 天线罩方位误差特性

图7 天线罩俯仰误差特性

图8是俯仰角度固定为0°时，方位误差随方位角度的变化曲线，拟合直线得出在-7°～+7°之间误差斜率为11.9%。图9是方位角度固定为0°时，俯仰误差随俯仰角度的变化曲线，拟合直线得出在-7°～+7°之间误差斜率为11.68%。此天线罩为圆锥性罩，方位、俯仰向误差特性对称。从图8和图9中测量出的天线罩误差特性数据表明，天线罩误差特性对称，表明了测试方法的可行性和准确性。

图8 方位误差变化曲线

图9 俯仰误差变化曲线

5.2 加入天线罩误差对雷达导引头系统影响仿真

把测得的天线罩误差特性数据，加入到导引头跟踪回路系统进行仿真。当俯仰角为0°，方位视线角按10 °/s线性增加，平台不加扰动时，输出角速率补偿前和补偿后结果如图10所示，其真实视线角速率10 °/s，曲线凸起0.4 °/s，补偿前后角速率误差分别为0.38 °/s与0.16 °/s。

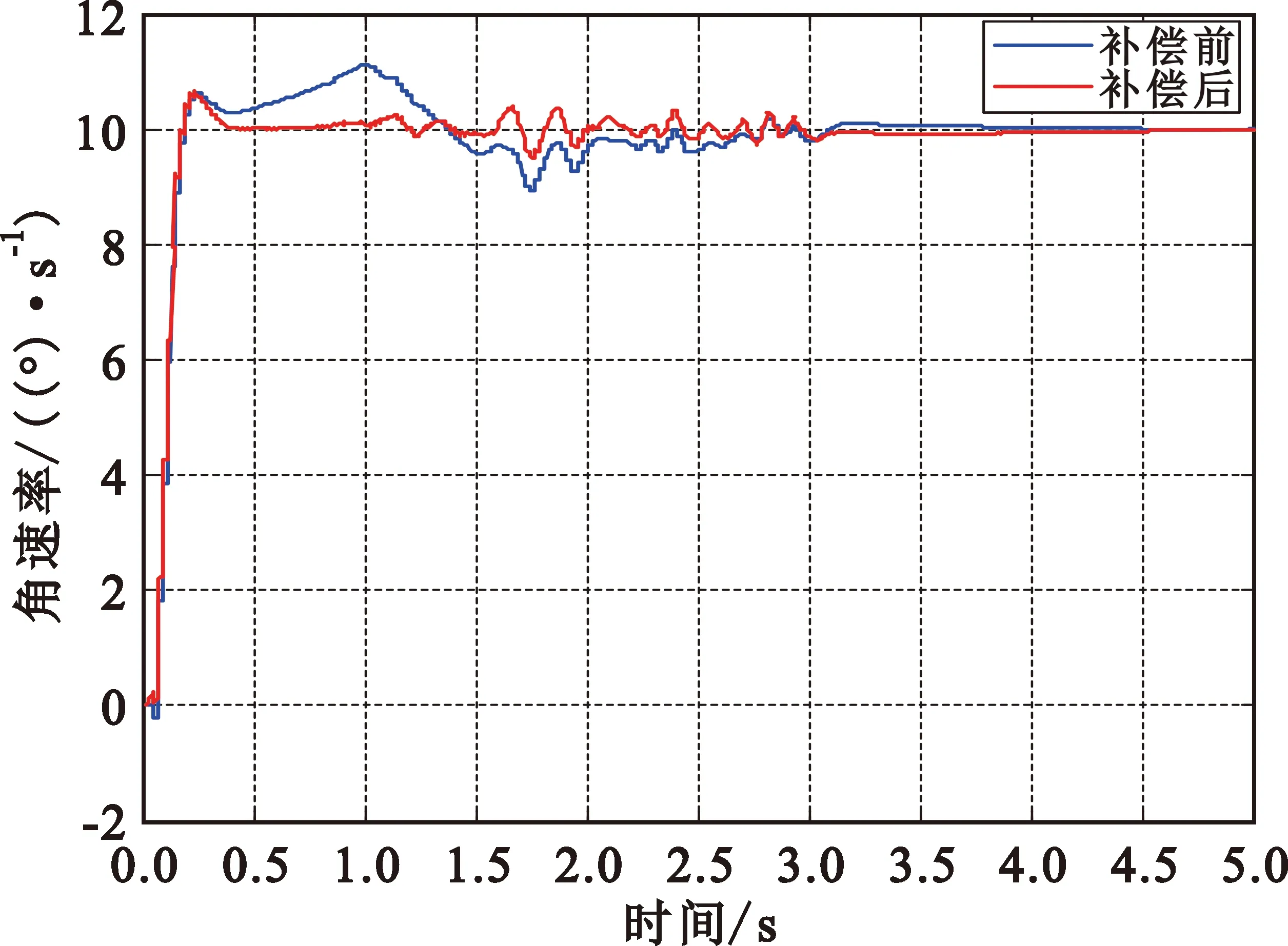
图10 无扰动视线角速率

当俯仰为0°，弹平台方位角摆幅7°，0.2 Hz扰动时，输出角速率补偿前后的结果如图11所示，补偿前后角速率误差分别为0.67 °/s与0.15 °/s。

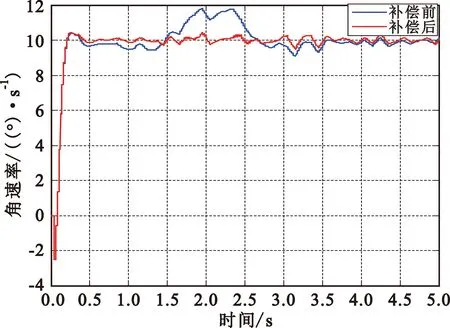
图11 加扰动视线角速率

上述分析结果表明补偿后曲线起伏减小，补偿效果有效，但未能完全补偿，其原因是误差表格数据是离散的，在表格数据两点之间插值取得的误差用直线近似代替，留有残差。

加入测量的天线罩误差特性后，对雷达导引头跟踪回路系统进行仿真，仿真结果表明采用补偿算法补偿后角速率误差小于0.2 °/s。

5.3 暗室试验验证

阵列墙喇叭模拟目标角度运动，方位运动角速率为10°/s，目标从-10°～+10°进行往返运动，雷达导引头安装上天线罩，始终保持跟踪目标状态进行角速率测量；同样方法测量俯仰角速率，经过补偿后的测试结果如图12和图13所示，对测试结果分析表明，补偿后方位角和俯仰速度误差分别为0.12 °/s和0.15 °/s，与仿真结果一致。

图12 方位角速率

图13 俯仰角速率

6 结束语

本文对单脉冲跟踪测角方法测量天线罩误差特性的原理、头罩数字补偿算法进行了阐述，并对测量数据和补偿方法进行分析、仿真与暗室试验验证，结果说明了此方法的可行性和有效性。多次参加了在试验场的飞试试验，试验结果圆满成功，进一步充分验证了此方法。本文所提方法可在其他工程研制中推广使用。该头罩补偿方法能对“一头”匹配“一罩”进行有效补偿验证，下一步将在“一头”匹配“多罩”或“一罩”匹配“多头”方面的补偿方法开展研究，进一步优化补偿方法，以提高测试效率和生产效率。