一种低轨卫星动态链路预算评估模型*

张朝贤,张 毅,徐 帆

(1.厦门大学嘉庚学院 信息科学与技术学院,福建 漳州 363105；2.中国西南电子技术研究所,成都 610036；3.福州大学 物理与信息工程学院，福州 350108)

0 引 言

随着移动互联网的飞速发展和智能终端产品设备的推广应用，人们对移动通信的速率提出了更高的要求。第五代移动通信系统(5G)旨在提供10～20 Gb/s的峰值速率以及100 Mb/s～1 Gb/s的用户体验速率，满足更为广泛的业务需求[1]。5G移动通信系统具有频带利用率高、传输速度快等优点，已经处于商用普及阶段。但是由于5G采用的超高频谱，会造成信号传播距离短、覆盖范围窄，需要大量基站来满足日常通信需求。对于人口密度较小的偏远地区而言，5G地面移动通信网络需要较大成本并可能造成资源浪费。相比较地面移动通信网络，卫星通信受地形影响小，覆盖范围广，信道容量大，能为全球提供服务。当今卫星通信系统正沿着天地一体化的方向发展，随着5G技术的逐渐进步，卫星通信的优点和地面通信的优点将充分融合，实现移动通信网络全球覆盖的目标指日可待[2-3]。

卫星透明转发系统因其星上处理简单，有利于迅速部署星地通信网络。因此，有必要研究地面信关站到卫星的馈电侧链路和卫星到终端用户的用户侧链路衰减，评估卫星透明转发通信系统的链路预算要求。目前，对于低轨卫星链路衰减及链路预算已有研究：文献[4]对卫星通信系统Q/V频段馈电侧链路的衰减进行了详细的计算，并得到链路的最大衰减、最小衰减和动态范围；文献[5]给出了低轨卫星的大尺度信道模型，并给出不同场景下无线电波在星地链路中传输时应考虑的衰减；文献[6-8]分别提出了大气吸收、云雾衰减、降雨衰减的具体计算方法。

上述研究仅给出某种链路衰减因素的计算方法或一侧链路的链路衰减值和链路预算，且未能在卫星星座覆盖下进行终端信噪比(Signal-to-Noise Ratio，SNR)分析。实际应用中的卫星中继通信系统需要考虑用户、卫星和地面信关站三者的具体地理位置和透明转发时卫星对信号放大情况，从而确定终端用户SNR是否满足要求，以及满足链路预算要求的卫星和信关站的等效全向辐射功率(Equivalent Isotropically Radiated Power，EIRP)。因此，本文对卫星透明转发通信系统进行建模，根据典型的低轨卫星星座参数分析终端用户的SNR分布以及对信关站的EIRP要求。

1 卫星透明转发通信系统模型

卫星中继通信系统模型包括地面信关站、卫星和终端用户三个部分。在下行链路中，无线信号从信关站发送到卫星，经过卫星对信号的放大后再从卫星发送给用户。

假设信关站的EIRP为Pt1(W/MHz)，卫星的EIRP为Pt2(W/MHz)，馈电侧链路增益为L1，用户侧链路增益为L2，星上噪声为Pn1(W/MHz)，终端噪声为Pn2(W/MHz)，卫星对信号的放大倍数为A，则终端用户接收的信号功率Ps为

Ps=(Pt1×L1)×A×L2。

(1)

经过馈电侧链路衰减后的信关站发射信号与星上噪声一起被卫星放大，这时信号功率应与卫星发射功率相等：

Pt2=(Pt1×L1+Pn1)×A。

(2)

星上噪声Pn1由文献[9]给出：

Pn1=10(TS+k+60)/10。

(3)

由公式(2)得出放大倍数A，进而得到卫星转发后接收端的总噪声功率为

Pn=Pn1×A×L2+Pn2。

(4)

终端噪声Pn2由文献[9]得到：

Pn2=10(10lg(T0+(Ta-T0)×10-0.1Nf)+Nf+k+60)/10。

(5)

式中：T0为环境噪声温度，取值为290 K；Ta为天线温度，取值为150 K；Nf为噪声指数，取值为1.2[9]。

由公式(1)、(2)、(4)得出系统信噪比为

(6)

将以上计算的信噪比与链路解调门限信噪比相比较，进而得出此系统各项指标是否满足链路预算的需求。由式(6)可以看出，如果馈电链路损耗过大，则星上噪声会被过度放大，导致接收信噪比恶化，此时两跳链路信噪比主要受馈电链路影响；如馈电链路质量较好，则两跳链路信噪比主要受用户链路影响。

2 卫星链路衰减分析

在卫星中继通信系统模型中，用户侧工作在Ka频段，因而可假设用户侧工作频率为20 GHz。假设用户终端所在地理位置天气状况为晴天，则用户侧链路衰减应考虑自由空间传播损耗、阴影衰落和大气吸收。

馈电侧工作在Q/V频段，因而假设馈电侧工作频率为50 GHz。在馈电侧链路衰减中，由于地面信关站通常处于空旷无人的地方，因而不考虑阴影衰落对馈电侧无线电波衰减的影响。在馈电侧中，信号的衰减包括自由空间传播损耗、大气吸收、云雾衰减和降雨衰减。

2.1 基本路径损耗

基本路径损耗(Basic Path Loss,BPL)包括信号在星地链路间的自由空间传播损耗(Free Space Path Loss,FSPL)和阴影衰落(Shadow Fading,SF)两部分。

2.1.1 自由空间路径损耗

电磁波在自由空间的传播是无线电波最基本、最简单的传播方式，在传播过程中，能量将随着电磁波传输距离的增加而扩散，由此引起的传播损耗称为自由空间路径损耗。当无线电波的传播距离为d(km)，载波频率为fc(GHz)，自由空间路径损耗LFSP(dB)可以表示为[5]

LFSP(d,fc)=32.45+20lg(fc)+20lg(d)。

(7)

对于地面的用户终端或信关站，与卫星的距离d可以通过卫星高度h0(km)和仰角θ(°)确定为[5]

(8)

式中：地球半径RE取值为6 371 km。

2.1.2 阴影衰落

阴影衰落是指卫星信号传送过程中遇到地面比如山丘或大型建筑物的大障碍对信号能量进行吸收和发散而造成的信号衰落。阴影衰落模型服从对数正态分布，当用dB为单位表示时，它是均值为0、标准差为σSF的正态分布[5]：

(9)

阴影衰落的大小与视距传播(Line-of-Sight，LOS)和非视距传播(Non-Line-of-Sight，NLOS)的概率有关。由于卫星用户大都分布在市郊或农村等地区，表1和表2分别给出了这些地区在不同仰角下的LOS概率以及对应的阴影衰落标准差[5]。

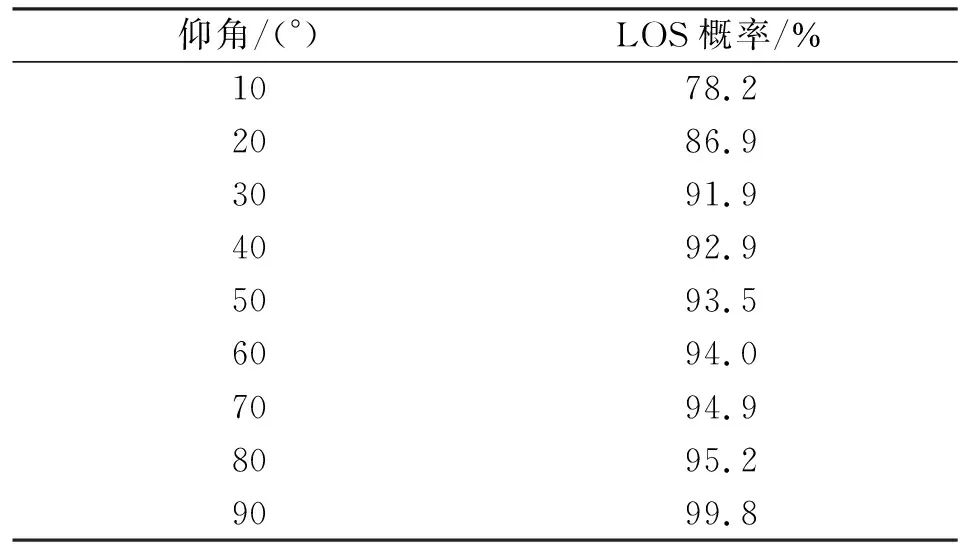
表1 郊区或农村场景中不同仰角下LOS概率

表2 郊区或农村场景中不同仰角下LOS和NLOS情况下阴影衰落

2.2 大气吸收

信号在卫星中继系统的传输过程中，星地链路间的多种气体成分会对信号能量造成衰减，这种衰减称为大气吸收(Atmospheric Absorption)。星地链路的用户侧工作在Ka频段，馈电侧工作在Q/V频段，所以本小节仅对频率为54 GHz以下的情况大气吸收进行计算。大气吸收主要取决于工作频率f(GHz)、仰角θ(°)、压强Bp(hPa)、相对湿度RH(%)和温度t(°C)[6]。

对于干燥空气，衰减率γ0(dB/km)为

(10)

式中：

(11)

(12)

(13)

(14)

(15)

(16)

(17)

对于水蒸气，衰减率γw(dB/km)为

(18)

式中：

(19)

(20)

(21)

对于干燥空气，其等效高度为

(22)

式中：

(23)

(24)

(25)

对于水蒸气，其等效高度为

(26)

式中：

(27)

当仰角5°≤θ≤90°时，计算出大气吸收Ag(dB)为

(28)

2.3 云雾衰减

无线电波在链路传输中受到大气中云雾粒子的影响发生信号衰减，这种衰减称为云雾衰减。(Cloud Attenuation)。云雾衰减主要与工作频率f(GHz)、仰角θ和液态水总柱含量L(kg/m3)有关[7]。

水的复介电常数可以表示为

(29)

(30)

衰减率系数K1(dB/km)表示为

(31)

当仰角10°≤θ≤90°时，计算出云雾衰减Ac(dB)为

(32)

2.4 降雨衰减

电磁波在降雨区域中由于雨水散射、吸收而造成信号衰减，这种造成信号强度的衰减称为降雨衰减(Rain Attenuation)。降雨衰减主要取决于工作频率f(GHz)、仰角θ(°)、地面站纬度φ(°)、圆极化角τ取45°、地面站海拔高度hs(km)和地面站平均年0.01%时间的降雨率R0.01(mm/h)[8]。

地面站的降雨高度hR(km)为

(33)

倾斜路径长度LS(km)为

(34)

水平投影LG(km)为

LG=LScosθ

。

(35)

衰减率γR(dB/km)为

(36)

其中：

(37)

(38)

上式中，当馈电侧工作频率为50 GHz时，kH为0.660 0，αH为0.804 8，kv为0.647 2，αv为0.787 1[10]。

水平缩减因子r0.01为

(39)

垂直缩减因子v0.01为

(40)

其中：

(41)

式中：当|φ|<36时，χ=36-|φ|，否则χ=0。

计算出平均年0.01%时间超出的降雨衰减Ar(dB)为

Ar=γRLRv0.01。

(42)

3 链路预算过程

低轨卫星透明转发通信系统链路预算的具体过程如下：

Step1 设置初始参数。设地球半径RE为6 371 km，卫星轨道高度h0为1 175 km，用户侧工作频率为20 GHz，馈电侧工作频率为50 GHz。星上噪声和终端噪声分别由公式(3)和公式(5)算出，卫星EIRP为4 dBW/MHz[9]。

卫星星座部署选取了Iridium、Teledesi和OneWeb 三个典型的全球低轨卫星星座，都采用极地轨道，其具体轨道参数如表3所示。

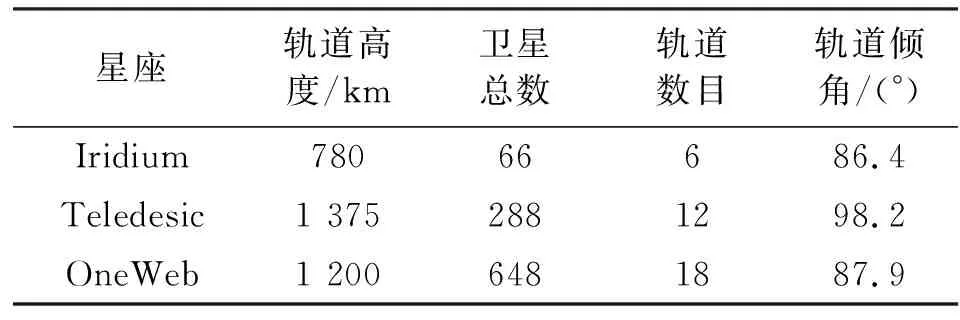
表3 典型低轨星座轨道参数

为了评估低轨卫星通信网络对我国大陆地区的覆盖情况，本文选取的终端用户地理位置分别是位于东、东南、南、西南、西、西北、北、东北8个方位的典型城市，选取的8个用户信息如表4所示；5个信关站信息如表5所示。

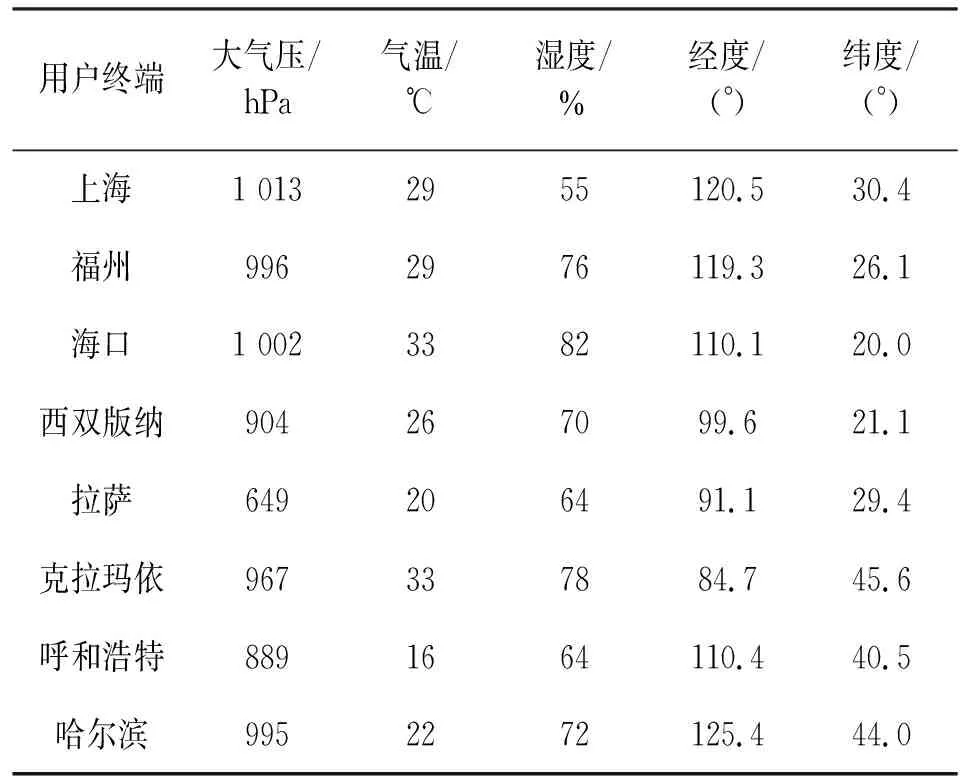
表4 8个用户终端信息

表5 5个地面信关站信息

Step2 计算两跳链路衰减。根据Step 1中星座参数，利用第1节的模型和第2节的链路衰减计算方法，对星座进行动态遍历，计算不同用户位置的用户侧和馈电侧最大链路衰减。在计算用户侧衰减时，阴影衰落采用表6给出的95%最大阴影衰落值，该数值根据表1和表2计算得出。

表6 不同仰角下95%概率的阴影衰落值

Step3 链路最小SNR分析。利用第1节中的公式(1)～(6)和计算出的两跳链路衰减值，计算出采用不同低轨星座时，在不同信关站EIRP下各城市用户终端对应的透明转发两跳链路最小SNR(即最坏情况下的SNR)。

Step4 信关站EIRP分析。计算出在不同解调门限的系统信噪比下各城市受到不同单轨道卫星数的影响，分析能满足链路解调门限信噪比要求的信关站EIRP。

4 仿真分析

4.1 链路SNR仿真分析

三种典型低轨星座覆盖下，各个城市对应的最小链路信噪比随着信关站EIRP变化的仿真结果如图1所示。

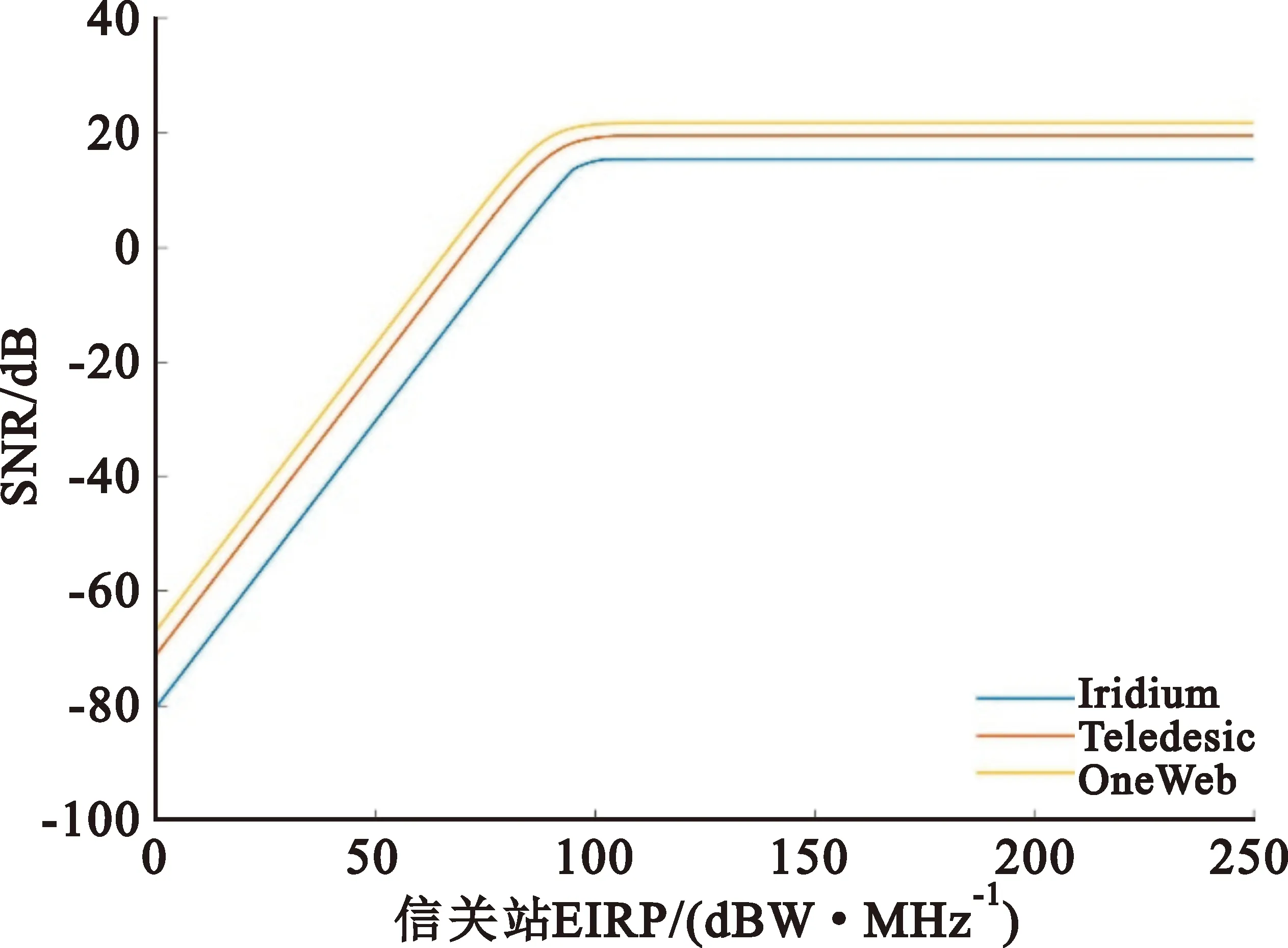
(a)上海

由仿真结果可以看出，当地面信关站EIRP较小时，链路信噪比随着信关站EIRP增大而增大，系统处于馈电受限情况；而当信关站EIRP足够大时，链路SNR不再随信关站EIRP变化，趋于恒定，此时的馈电链路饱和，SNR仅由用户链路决定。

在馈电饱和的情况下，从所有8个城市的仿真结果来看，三个典型低轨星座中SNR最大的都是OneWeb，其次是Teledesic，而Iridium最差。这是因为OneWeb星座卫星数量最多，密度最大，虽然其轨道高度比Iridium要高，但用户仰角最大，仍然可提供三者中最大的SNR；Iridium星座卫星数过少，虽然其轨道高度最低，但是过小的用户仰角导致其SNR最小。

需要指出的是，本文给出的两跳链路SNR计算方法考虑了馈电链路和用户链路的共同作用。同一卫星星座在信关站EIRP不同时，由公式(6)得到的最差SNR对应的接入卫星轨道位置可能不同，从而导致对不同星座的SNR比较在EIRP不同区间内的大小关系不一致。如图8所示的哈尔滨市接收SNR，Iridium曲线和Teledesic出现了交叉，在EIRP小于100 dBW/Hz时，Iridium星座的接收SNR高于Teledesic，而在EIRP大于100 dBW/Hz时则相反。表7给出了哈尔滨市在Iridium星座覆盖下，不同EIRP的最差SNR对应的用户侧和馈电侧损耗。从表中可以看出，EIRP小于100 dBW/Hz对应的馈电损耗较大，而大于100 dBW/Hz对应的馈电损耗较小，说明不同EIRP时用户最差SNR对应的卫星轨道位置不同，验证了EIRP对接入卫星位置的影响。

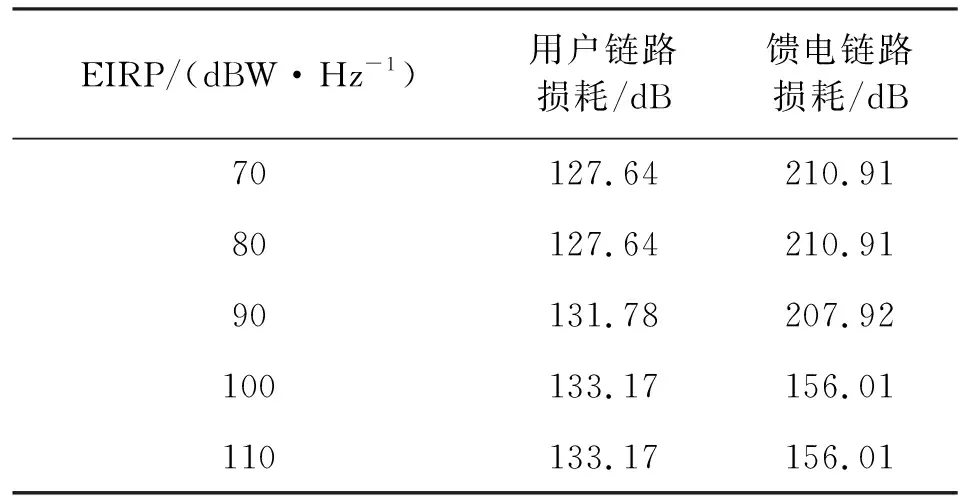
表7 哈尔滨市不同EIRP的用户侧和馈电侧损耗

4.2 解调门限所需信关站EIRP分析

当链路解调门限SNR要求为-10～10 dB时，在系统信噪比最差情况下如要保证卫星通信链路能正常工作，不同星座在不同城市所需要的地面信关站EIRP如图2～4所示。

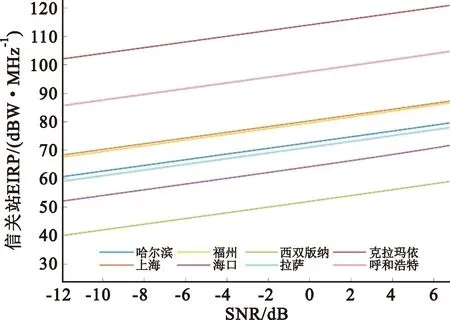
图2 Iridium星座对应各城市门限SNR所需信关站EIRP

图3 Teledesic星座对应各城市门限SNR所需信关站EIRP

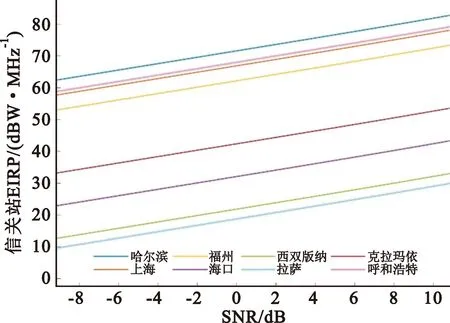
图4 OneWeb星座对应各城市门限SNR所需信关站EIRP

对比图2～4可知，在相同的解调门限下，各用户所需要的信关站EIRP随用户地理位置的不同而产生较大差异；在卫星轨道方面，总体上相同SNR解调门限对EIRP的要求按Iridium、Teledesic、OneWeb依次减小。参照5G-NR物理层设计，在最低阶MCS(QPSK调制，码率0.1172)时，误块率为0.001对应的解调门限为-6 dB[11]，则可以看到不同星座下各个城市所需的信关站EIRP，Iridium为45～105 dBW/MHz，Teledesic为12～100 dBW/Hz，OneWeb为12～65 dBW /Hz。

5 结束语

本文通过对卫星透明转发通信系统的建模，提出了低轨卫星动态链路预算评估模型，为透明转发卫星互联网链路预算设计提供参考。利用大尺度信道模型和链路衰减的相关计算方法，给出国内典型城市在不同的典型低轨卫星星座下随着信关站EIRP变化的链路信噪比，以及不同卫星星座、不同城市下解调门限对EIRP的要求。本文提出的方法考虑了馈电链路和用户链路的共同作用，链路预算结果能够较好地评估卫星星座设计、用户地理位置对两跳链路SNR的影响。

卫星星座设计需要进行综合考虑，才能在合理的EIRP水平下使得SNR达到解调门限，实现较好的覆盖。