卫星位置高时空分辨率实时预报的FPGA实现*

郑金秀

(中国西南电子技术研究所,成都 610036)

0 引 言

航天测控地面站的研制过程中，常常需要卫星信号模拟器，产生目标信号，以支撑测控相关装备的设计验证。

对卫星信号模拟往往要求进行角误差、时延及多普勒频率的模拟。角误差受卫星当前位置与接收天线指向角的影响，而时延和多普勒频率则由卫星与接收平台之间的相对位置及其变化决定。在某些应用中，常常要求卫星模拟器具有较高的时延和多普勒频率模拟精度，所以，连续地获取卫星位置并根据接收天线当前位置及指向计算角误差、时延及时延变化，进而逐采样点地计算卫星模拟信号，是一种极为有效的卫星信号模拟方法。卫星模拟信号的采样率越高，相应的卫星位置采样周期越小，再结合高的卫星位置计算精度，角误差、时延和多普勒频率的模拟精度则会越高，越接近真实情况。

卫星位置获取可以通过存储查表和实时计算两种方式。存储查表方式是把卫星运行历经的位置数据按顺序存储起来，然后通过实时查表的方式获取卫星当前的位置。该方法难以实现卫星位置的高时空分辨率。对应于目标模拟信号的采样周期，若卫星位置采样频率为100 Msample/s，卫星位置数据若采用3个20位数据表示,则1 s的位置数据需要750 MB的存储空间，十分庞大。

本文基于现场可编程门阵列(Field Programmable Gate Array，FPGA)器件，根据星历中的轨道参数和摄动参数进行卫星位置的实时计算设计，以在每个目标模拟信号的采样时刻给出高精度的卫星位置数据，最大限度支撑模拟器尽可能精确地模拟误差角、时变多普勒等，实现卫星目标信号的高时空分辨率模拟。

1 卫星位置计算

通过卫星下发的广播星历参数模拟卫星运动轨迹，星历参数包括轨道参数和修正轨道的摄动参数，每2 h更新一次，在参考时间前后1 h内，卫星的误差可以控制在米级别[1]。星历中的轨道参数包括椭圆半长轴a、椭圆离心率e、轨道倾角i、升交点赤经Ω0、近地点角距ω、真近点角f。星历中的摄动参数包括星历中的摄动参数包括升交点角距余弦调和校正振幅Cμc、升交点角距正弦调和校正振幅Cμs、轨道半径余弦调和校正振幅Crc、轨道半径正弦调和校正振幅Crs、轨道倾角余弦调和校正振幅Cic、轨道倾角正弦调和校正振幅Cis、平均运动角速度校正值Δn、轨道倾角对时间的变化率id和轨道升交点赤经对时间的变化率Ωd[2]。

本文采用了轨道平面坐标系、WGS-84坐标系(协议地球坐标系)和站心坐标系，最后根据卫星在站心坐标系中的位置得到卫星相对地面接收站俯仰角、距离和方位角[3]。

卫星轨道的平近点角M可以通过平均角速度n和运行时间计算得到。平近点角与卫星运行的角度——偏近点角可通过解开普勒方程得到，该方程不能通过直接求出数值解，需迭代几次求解[4]。整理得到开普勒方程如下：

E=M0+n(t-t0)+esinE。

(1)

在求得卫星运行的偏近点角后，再求解真近点角f、向径r′和角距μ′，整理得

(2)

求出的极坐标系坐标可以直接参与运算，但是为了得到较高精确度的采样点，这里根据星历参数的摄动对轨道参数修正：

(3)

修正后的向径、升交角距和轨道倾角参与计算卫星轨道坐标系位置坐标，整理得

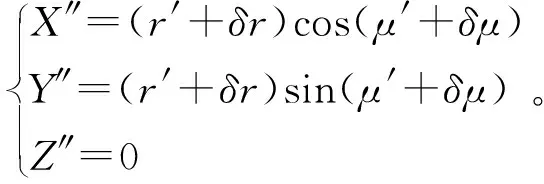
(4)

根据求得的卫星在轨道平面上的实时位置(X″,Y″,Z″),再利用式(5)得到卫星在WGS-84坐标系中的实时位置(Xk,Yk,Zk)[5]：

(5)

利用WGS-84坐标系与站心坐标系之间的转换关系式，得到卫星在站心坐标系中的向量(Δe,Δn,Δu)T，整理得到式(6)所示的计算公式：

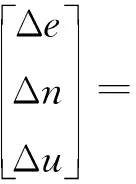
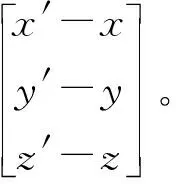
(6)

式中：(x,y,z)T为地面接收站在WGS-84坐标系中的位置坐标，(x′,y′,z′)T为卫星在WGS-84坐标系中的位置坐标，λ和φ分别式地面接收站的经度和纬度。利用式(7)可以得到卫星相对于地面接收站的距离、俯仰角、方位角：

(7)

式中：I、θ、α分别表示地面观测站与卫星之间的距离、俯仰角和方位角；θ的范围在(0,π/2)之间，与天顶角之间为互余关系。

2 卫星位置计算FPGA实现

根据第1节所述卫星轨道计算过程综合设计FPGA实现过程，为了实现高时空分辨率，也就是高数据精度和采样率，从模块设计、流水设计、精度控制三个方面完成FPGA设计。

图1所示为计算流程图。整个计算过程可以划分成5个模块进行，分别为t更新模块、t时刻卫星参数计算、轨道平面坐标计算、WGS-84坐标系坐标计算、站心坐标系坐标计算和相对位置计算。通过在信号线上插入缓存模块的方式同步数据，完成流水设计。在模块之间建立Valid和Ready控制信号，来判断数据传输的有效性。

图1 卫星轨道计算系统框图

图1中的t更新模块是在输入t1的基础上进行循环迭代，将更新后的t送入寄存器进行缓存。图1中也给出了各个计算模块之间的数据传输关系以及数据位宽，所有数据均由有符号浮点数量化成了有符号定点数，以达到提高运算速率和减少资源占用的目的。

2.1 功能模块实现设计

根据第1节中算法的叙述和图1所示计算流程，图2给出了t时刻卫星参数计算模块的设计框图，框图中的轨道参数和摄动参数都是星历下发的参数。

当calc_en为由低电平跳变到高电平时，整个模块开始工作。同理，其他子模块在对应的控制信号拉高的时候开始工作，送出输出参数和控制信号。部分数据信号插入缓存，以达到数据同步的目的。若模块计算一个数据需要T时间，某个时刻输入t，则同时输出(t-T)时刻的μ、r、i、Ωk，T时间后输出t时刻的参数，通过预先偏移时间T完成实时计算。

图2 t时刻卫星参数FPGA设计框图

在图2中的计算除了加、减、乘等简单运算，还涉及到了大量了的三角函数、反三角函数和开方运算这样的复杂运算。本文采用CORDIC算法来进行这些复杂运算的求解。CORDIC算法相比于ROM查找表和多项式近似法等方法，节约了硬件资源[6]，增加角度的旋转次数就可以提高精度，方便FPGA的实现。CORDIC算法的实现可采用循环迭代结构或流水线结构，流水线结构能够提高系统的工作频率，循环迭代结构节约硬件逻辑资源，应根据系统的速度和资源占用的需求来选择合适的实现结构。图3为CORDIC算法实现的硬件结构图，其采用流水线结构来实现系统速度的提升。

图3 CORDIC算法硬件结构图

如图3所示，CORDIC算法将三角和反三角等函数的计算转化成加、减和移位等便于硬件实现的操作。arctan(2-i)查找表通过一个小容量的ROM实现。图3所对应的迭代公式为

(8)

式(8)中的zi为角度累加器，在计算三角函数时，zi=0时结束迭代。di的正负由角度累加器来进行判断，di=1时，表示逆时针旋转；di=-1时，表示顺时针旋转。式(8)中对tanθi=2-i做了近似的代替，这使得复杂的超越方程成了简单的移位运算，大大提升了运算效率。

CORDIC算法的旋转模式可以求解正弦函数sin和余弦函数cos，向量化模式可以求解反正切函数arctan和向量模值。

根据文献[7],在圆坐标系中，对输入向量(X0,Y0)经过n次角度旋转，得到结果为

(9)

在圆坐标系中向量化模式的原理和旋转模式是类似的，唯一的不同就在于，输入向量通过n次旋转后与X轴对齐，旋转的方向由Yi决定。

CORDIC旋转器对输入向量旋转n次之后，得到的结果为

(10)

2.2 时序设计

为了获得高速的运算速度，整个FPGA程序设计采用了流水线技术。流水线技术只需占用少量的硬件资源，就可以大大的提高运算速度，是以面积换取速度的典型设计方法[8]。将整个卫星轨道的运算系统进行分解，分解成小规模的运算单元，将运算结果存储在寄存器中，隔离两个运算单元，该运算单元在下一个时钟周期又根据输入进行计算，从而实现流水线。这样大大缩短了整个系统在首次延迟后的运算的时间。本文中FPGA的流水线结构图如图4所示。

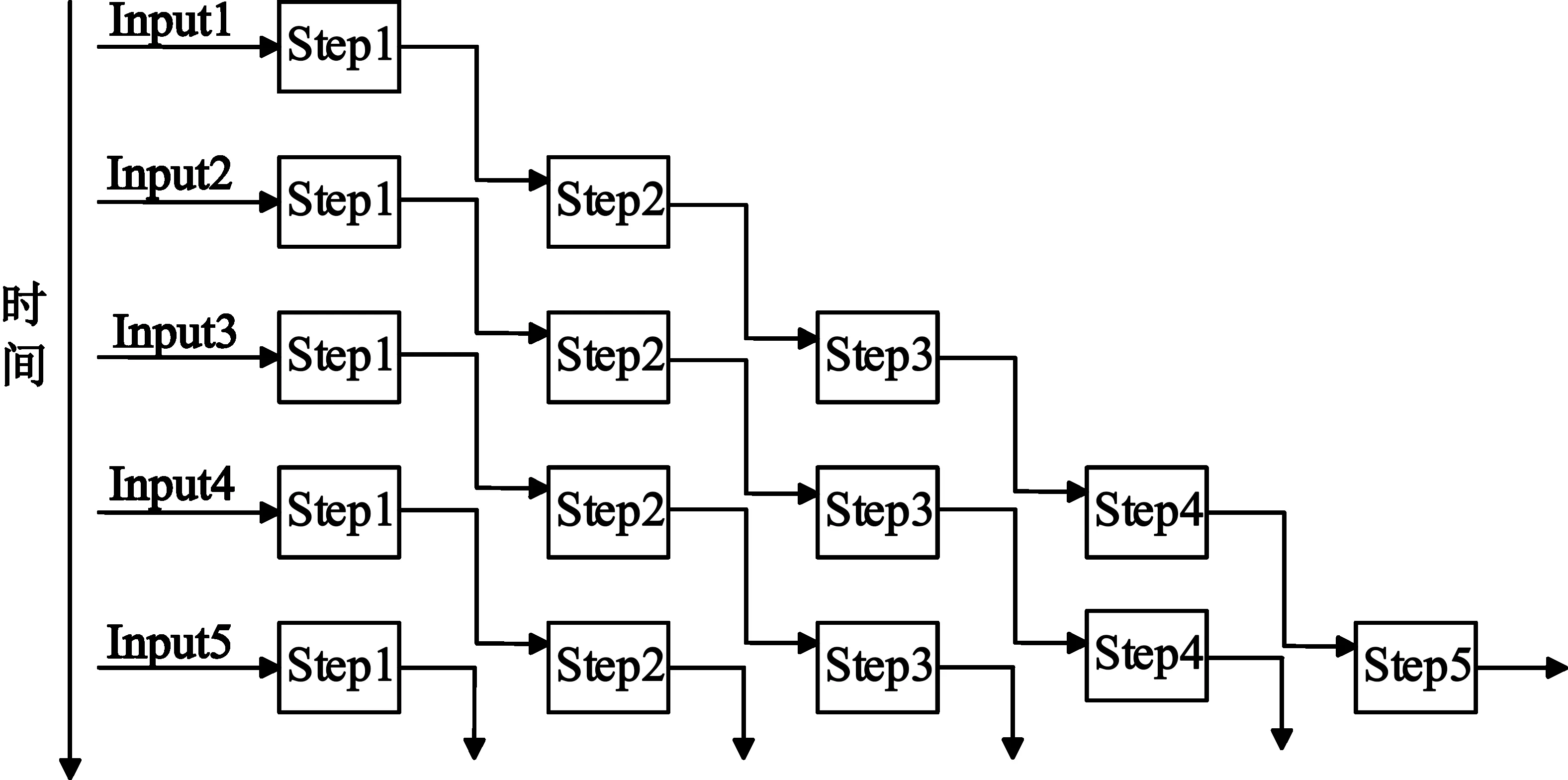
图4 流水设计

根据图4的流水结构图可以看出，整个系统被分解成了5个大的运算模块构成4级流水系统。每一个运算模块中也采用了流水式的设计，以提高每个模块的运算速率。第1级流水，Step1读取卫星星历参数、更新后的观测时间t和控制信号，根据图2中所设计框图的流程运算，输出t时刻摄动校正后的μ、r、i、Ωk和控制信号，将其存入1级寄存器，在input2时重复上述操作。第2级流水，Step2读取控制信号和存入1级寄存器中的数据，进行卫星在轨道平面的位置计算，将计算结果和控制信号存入2级寄存器，再读取1级寄存器中更新后的数据重复上述操作。第3级流水，Step3读取控制信号和存入2级寄存器中的数据，进行卫星在WGS-84坐标系的位置计算，将计算结果和控制信号存入第3级寄存器，再读取2级寄存器更新数据后和控制信号重复上述操作。第4级流水，Step4读取第3级寄存器中的数据和控制信号，计算卫星在WGS-84坐标系中的坐标，将运算结果和控制信号存入第4级寄存器，再读取第3级寄存器更新后的数据和控制信号重复上述操作。最后如图4所示，整个系统就实现了流水并行式的操作。每一模块都在时时刻刻进行运算，不需要等上一模块的结束，大大地提高了整个系统运算速率。

系统的首次延迟为1 374个时钟周期，大约耗时1.4 μs。当整个系统流动起来之后，一个cycle的延时为36个时钟周期，因此在时钟频率为100 MHz时，36 ns就能计算出一个结果。程序的最终的资源使用情况：寄存器使用37 468；LUT使用26 686；RAM/FIFO使用6；DSP48E1s使用225。

2.3 数据量化与精度设计分析

相比于浮点数，定点数在FPGA中占用的资源更少，运算速度更高。在精度满足要求的情况下，定点数相比于浮点数在FPGA中更加合适。因此在本文设计的卫星轨道计算系统中，将有符号浮点数量化成有符号定点数，以达到更少的资源占用和更高的运算速度。在有符号浮点数量化成有符号定点数的过程中，小数有效位宽不同量化后的定点数精度就不同，小数有效位宽越大，则量化后的定点数精度就越大。若量化后的小数有效位宽为n，则定点数的精度为1/2n。同时在对浮点数进行量化时，在数据不溢出的情况下，存在一定的量化误差。比如数7.512，在量化成1位符号位、6位整数位和1位小数位的情况下，量化后的定点数二进制如图5所示，表示的十进制为22+21+20+2-1=7.500，因此产生了0.012的量化误差。通过小数位的所在位置，能够有效地将定点数还原成与之对应的十进制数值。

综上所述，人民币汇率政策变动的宏观经济效应十分显著，但影响的方向和程度与人民币汇率所处的周期密切相关。具体而言，顺应汇率周期的制度改革对宏观经济有正向影响，而逆汇率周期的制度改革对宏观经济有负向影响；从汇率制度改革的长短期效应来看，汇率制度变化往往在短期内对宏观经济的冲击较大，而在长期逐渐趋于平稳。汇率制度变化对宏观经济的冲击方向在长短期并不一致，短期内有效的政策从长期来看可能有失误，短期内造成“阵痛”的政策从长期来看意义颇大；此外，不仅汇率制度变化对宏观经济有影响，宏观经济的运行形势对汇率制度变化也有相当大的制约作用，若两者出现“错配”，将会对宏观经济稳定和国内金融安全带来巨大的压力。

图5 8 b定点数结构

浮点数量化成定点数的具体量化公式为

(11)

式中：s为符号位的值，ffloat、lbw分别表示小数位宽和总的量化位宽，xi表示有效位。

整个运算过程中，每一个参数的小数部分量化位宽，对最后的运算结果有极大的影响。在保证精度的情况下，小数的有效位宽要尽可能地小，避免FPGA资源浪费。因此本文采用控制变量法对每一个参数做小数有效位宽对结果的误差分析，以寻找每个参数的最佳小数部分量化位宽。图6所示为卫星矢径长度r的小数有效位宽对距离精度的影响。

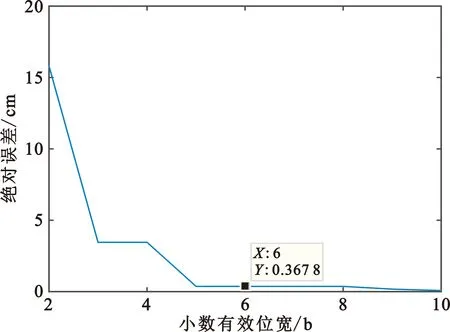
图6 卫星矢径长度对距离精度影响

图6纵坐标表示的绝对误差是相关参数量化后计算的距离结果和距离理论值之间绝对误差。从图6可以看出，当卫星矢径长度r的小数有效位宽为5 b、6 b、7 b和8 b的时候，绝对误差是比较接近的。综合资源占用和精度要求方面考虑，取r的小数有效位宽长度为6 b，则此时的绝对误差为0.367 8 cm。根据图6中的分析手段，依次对每个参数量化后的小数有效位宽对精度的影响进行分析，表1给出了部分参数量化后的小数有效位宽对误差的影响。对比三个小数有效位宽所带来的误差可以得到的结果是，当取到合适的小数有效位宽后，再增加小数的有效位宽并不能使误差明显减小。因此，本文将中间的小数有效位宽作为对应参数的最佳小数有效位宽。

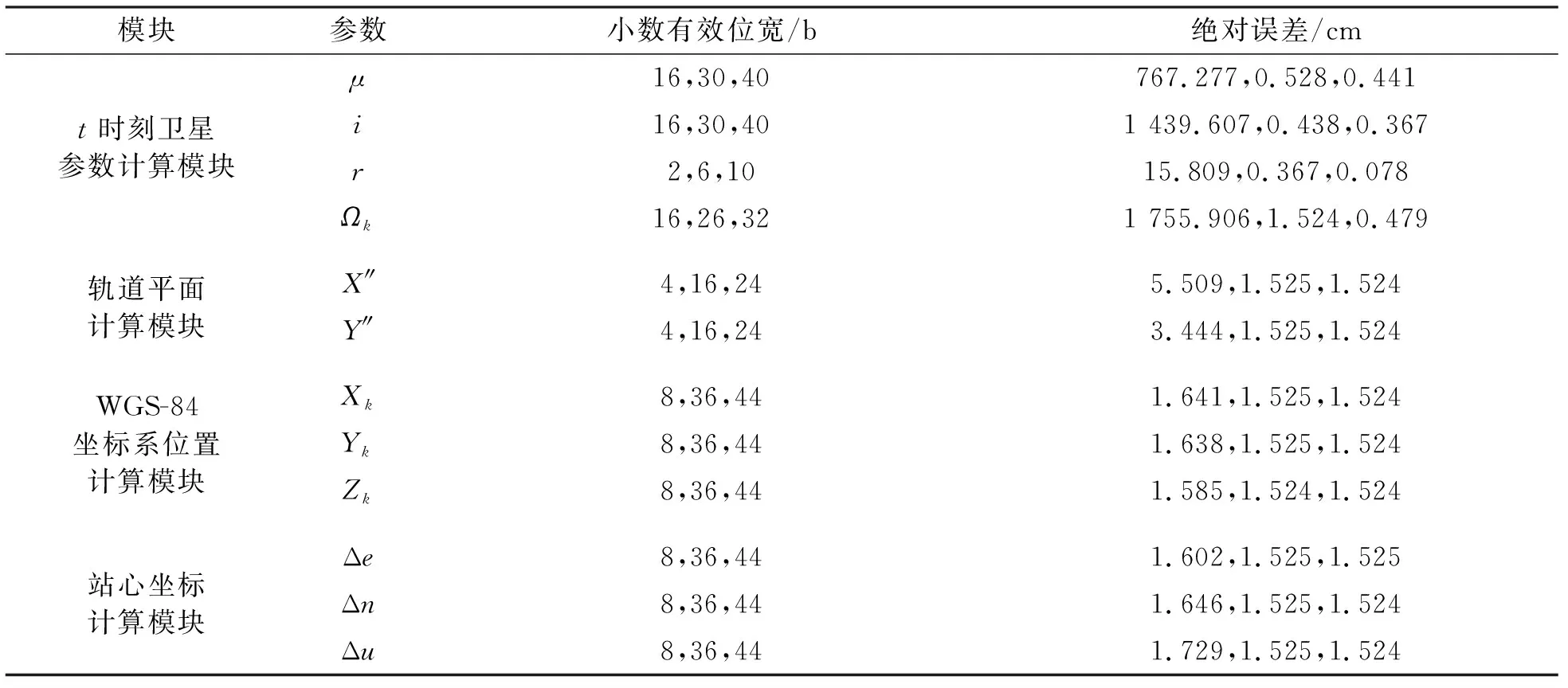
表1 部分参数量化小数有效位宽与误差关系

3 仿真结果

为了验证整个卫星轨道实时计算系统的正确性，本文借助ISE DesignSuite14.7软件搭建卫星轨道实时计算系统并进行仿真实验。卫星星历参数和参考时间来源于卫星PRN-1在某日下发的一组参数，该卫星轨道高度为20 200 km，属于中轨GPS导航卫星；精确度和实时性基于卫星星历，具体参数取值如表2所示。

表2 输入数据参数表

将表2中的卫星星历参数和观测时间t，以及地面接收站的WGS-84坐标系坐标参数作为仿真实验的输入，构建仿真环境，进行仿真实验。本文将100 MHz作为仿真的时钟频率，根据表2中的参数仿真出来的结果如图7所示。

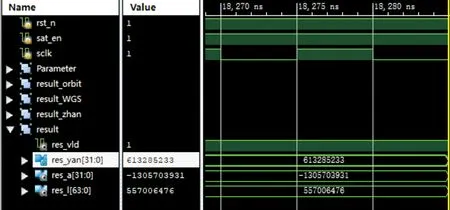
图7 卫星位置计算FPGA实现仿真

图7中res_yan、res_a和res_I分表表示仰角、方位角和距离，其中res_yan和res_a均为29 b小数位的定点小数，res_l为5 b小数位的定点小数。将方位角转换为非定点小数后，还应该将其变换到-π/2～π/2的范围。将结果转换成有符号浮点数，分别为res_yan=1.142 332 764 342 427、res_a=0.709 529 560 180 858和res_I=17 406 452.375，而理论数据分别为1.142 332 789 655 088、0.709 529 472 943 342和17 406 452.417 841 10。通过对比理论数据和仿真数据可以得出仿真数据和理论数据是非常接近的，验证了整个卫星轨道实时计算系统的正确性。

4 结 论

本文利用FPGA进行卫星位置的实时高时空分辨率预报，采用CORDIC算法实现开方、三角函数和反正切运算，采用流水线技术提高整体的运算速度。采用该方法，卫星信号模拟器在生成每一个采样点的模拟信号时都可以依据更新的卫星位置对时变的角误差、时变的时延、时变的时延变化或时变多普勒进行高精度的模拟，与存储查表预报法相比，可以避免难以实现的海量存储问题。