扩张调节片结构点阵拓扑轻量化技术研究

2022-08-26宋经远邵万仁贾东兵金文栋杜桂贤

机械工程师 2022年8期

宋经远，邵万仁，贾东兵，金文栋，杜桂贤

（中国航发沈阳发动机研究所，沈阳 110066）

0 引言

点阵结构作为一种新型轻质功能结构，由规则的多孔单胞结构按一定规律排列构成，具有轻质量、高承载力、高刚度、高孔隙率和能量吸收等一系列优异特性，同时在减振、降噪和散热等方面具有比传统结构更加优异的性能。因此，该类结构在航空航天、船舶工程和轨道交通等领域得到广泛关注，能够满足关键零部件的轻量化和功能设计需求。

廖中源等[1]根据实际载荷提出一种均匀化的多尺度拓扑优化方法来优化变密度点阵结构体，并以汽车连杆为例，通过HyperWorks商业软件来验证提出方法的正确性。柏龙等[2]和徐亮等[3]基于体心四方点阵结构模型，以材料尺寸和成型工艺为约束条件，以单胞构型尺寸为设计变量，以初始刚度、塑性强度、密度为多目标评价参数，建立目标优化数学模型，为轻质点阵结构的优化设计提供理论依据。王向明等[4]针对飞机结构与功能的一体化需求，对点阵结构的制造工艺、性能和应用背景进行系统化描述，对点阵结构应用的局限性进行了分析。方泽辉等[5]采用拓扑优化方法结合三维打印技术及泡沫填充技术设计了泡沫填充点阵结构，并通过材料实验机研究该类结构在准静态压缩条件下的力学行为。杜义贤等[6]基于拓扑优化技术，采用能量均匀化方法建立关于周期性点阵结构的优化分析模型。孟传伟等[7]以三维悬臂梁为研究对象，采用变密度拓扑优化方法对点阵结构进行优化，在上述优化的基础上，进一步进行尺寸优化，设计出性能优越的杆件结构。朱杰等[8]采用有限元商业软件ANSYS和MATLAB，通过拓扑优化和尺寸优化对风力机叶片进行轻量化设计。徐伟等[9]采用了拓扑优化及尺寸优化方法对复合材料点阵结构进行优化设计。朱健峰等[10]基于拓扑优化原理对多种点阵结构进行仿真和实验分析，为点阵结构的轻量化设计提供理论依据。雷鹏福等[11-12]以航空构件的轻量化设计及其优化为研究背景，采用增材制造工艺将点阵结构填充于结构内部，在实现结构轻量化设计的同时带来新的功能特性。

本文在现有研究的基础上，以扩张调节片为研究对象，基于均匀化方法，采用MATLAB和ABAQUS软件实现对扩张调节片结构的点阵拓扑优化，以此得到点阵结构单元中的相对密度分布。在点阵拓扑优化的基础上，采用OPTISTRCUT软件对点阵结构进行尺寸优化分析，从而获得最佳的点阵结构尺寸类型，以此实现对扩张调节片结构的轻量化设计研究。

1 扩张调节片结构描述

图1所示为扩张调节片结构的几何模型示意图。图1中的深色区域表示扩张调节片的优化设计空间，本文将上述深色区域中实体单元进行点阵拓扑优化，在保证扩张调节片结构整体刚度的前提下，实现对扩张片结构的轻量化设计。同时指出，扩张片结构模型的约束位置为左端孔和模型支架上方的孔，扩张片结构的载荷工况是在模型底部施加随位移变化的均布压强。

图1 扩张调节片结构示意图

2 扩张调节片结构点阵拓扑优化流程

图2所示为扩张调节片结构点阵拓扑优化的流程。本文对扩张调节片的结构轻量化设计是根据上述流程图展开的，具体研究思路为：首先通过均匀化方法对点阵结构中的点阵胞元的力学性能进行等效，并将等效的力学性能参数拟合为与点阵胞元相对密度相关的函数；然后根据已知的模型约束和载荷工况，以点阵胞元的相对密度为设计变量，以最小化柔度为目标函数，采用MATLAB软件进行点阵拓扑优化，得到点阵胞元的相对密度分布。与此同时，根据已获得的点阵胞元的等效力学性能参数，采用等效体积单元法，将点阵胞元等效成实体单元，并通过ABAQUS软件进行有限元分析，以此确定点阵胞元的单元节点等相关信息；然后根据点阵胞元的相对密度分布和单元节点，采用OPTISTRCUT软件对扩张调节片结构进行参数建模，并对扩张调节片结构进行点阵拓扑优化；最后在上述点阵拓扑优化的基础上，以最小化质量为目标函数，通过对点阵胞元的尺寸优化实现扩张调节片结构的轻量化设计。

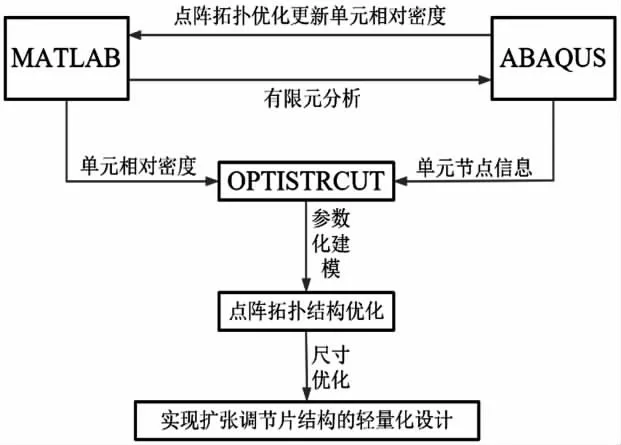
图2 点阵拓扑优化流程图

3 扩张调节片结构点阵拓扑优化分析

3.1 低密度点阵拓扑优化结果分析

图3所示为扩张调节片粗网格结构的有限元模型示意图，加粗优化设计区域网格的目的是得到稀疏点阵结构（低密度点阵结构），便于开展低密度点阵拓扑优化分析，分析结果如图4（a）所示。为了进一步显示点阵拓扑优化的效果，图4（b）为局部放大示意图。从图4中可以看出，点阵拓扑结构出现截面的梯度变化，这是由于只考虑1D单元的应力约束，没有考虑结构整体体积和质量的限制。

图3 扩张调节片粗网格结构示意图

图4 扩张调节片结构低密度点阵拓扑优化结果示意图

在上述点阵拓扑优化的基础上，在保证扩展调节片结构强度和刚度的基础上，对结构进行尺寸优化以实现结构的轻量化设计，尺寸优化的结果如图5所示。

图5 扩张调节片低密度尺寸优化结果示意图

最终优化结果表明，尺寸优化的过程中通过调整1D单元的截面尺寸，实现结构的“梯度”变化，从而实现结构材料的合理分布。通过测量整个模型的质量，模型优化最终的质量为1.784 kg，与原模型的2.4 kg相比，减重25.67%。为了进一步说明点阵拓扑和尺寸优化效果，对优化后的模型进行静力学仿真，位移和应力仿真结果分别如图6和图7所示。

从图6可以看出，在非线线性变化的均布压强载荷下，结构的最大变形位置出现在模型端部，数值为1.801 mm，原模型的最大位移为2.068 mm，结构整体刚度提升了12.57%。从图7可以看出，经过点阵拓扑优化以后，扩张调节片结构的最大等效应力为373.1 MPa。与点阵拓扑优化前的最大等效应力437.515 MPa相比，扩张调节片的强度有了大幅度的提高。

图6 高密度扩张调节片位移变形云图

图7 高密度扩张调节片应力变化云图

3.2 高密度点阵拓扑优化结果分析

与上述低密度点阵拓扑优化相比，高密度拓扑优化是在扩张调节片的点阵拓扑优化区域采用细化的网格。点阵拓优化结果如图8所示。

图8 扩张调节片结构高密度点阵拓扑优化结果示意图

在点阵拓扑优化的基础上，对扩张调节片进行尺寸优化，尺寸优化的结果如图9所示。

图9 扩张调节片高密度尺寸优化结果示意图

最终优化结果表明，在原模型的基础上，对1D单元进行了尺寸优化，细小结构被删除，点阵结构出现了新的结构。通过显示截面属性查看表明，点阵结构的梯度性增强，在满足结构刚度、强度的条件下保证结构的轻量化。通过测量得到优化后的点阵结构其质量为1.51 kg，比原模型减重了37.10%。为了进一步探究点阵拓扑和尺寸优化效果，对优化后的模型进行静力学仿真，位移和应力仿真结果分别如图10和图11所示。

从图10可以看出，模型的最大位移出现在未约束的末端，其数值为1.802 mm，原模型最大位移为2.068 mm，刚度提升12.86%。从图11可以看出，实体结构的最大等效应力为398.2 MPa，与原模型的437.515 MPa相比，强度有了大幅提高。

图10 低密度扩张调节片位移变形云图

图11 低密度扩张调节片应力变化云图

3.3 点阵拓扑优化结果选型

经过上述研究，为了得到更合理并且便于加工的点阵结构，本节将在点阵结构最大长度分别为10、12、14、16、18、20 mm的条件下，进行点阵拓扑优化，以此获得最佳的点阵拓扑结构。扩张调节片结构的边界条件是约束结构端部和结构上部螺栓孔的自由度，扩张调节片结构的载荷工况是在结构底部施加梯度变化的压强载荷，如图12所示。

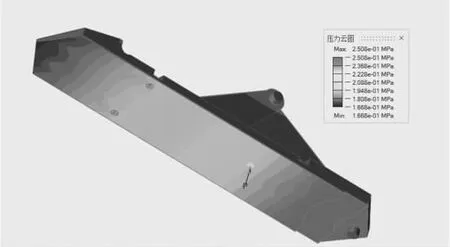
图12 扩张调节片边界条件和载荷工况示意图

同时指出，采用点阵直径为点阵长度1.0 mm～0.2倍格栅长度的方式，对扩张调节片区域进行点阵拓扑优化设计，扩张调节片结构在不同点阵结构最大长度下的点阵拓扑优化结果如图13所示。

图13 不同点阵结构最大长度下的点阵拓扑优化结果

从图13可以看出，当点阵结构较密时（点阵结构最大长度较小时），点阵结构有更多的自由度进行优化且优化呈现为不同梯度。但是较密的点阵结构为增材制造和后处理过程带来了困难。随着点阵结构最大长度的增加，孔隙率逐渐增加，点阵梯度变化不明显，截面尺寸变化较为明显，增材制造和后处理过程的难度有所降低。

为了进一步说明上述点阵拓扑优化效果，给出了点阵拓扑优化后的静力学仿真结果，具体如图14所示。结果表明，当点阵结构最大长度为10 mm时，结构最大的位移为2.119 mm，大于原模型的2.098 mm，在刚度方面存在较大的不足。但是在结构轻量化方面，减重了21.38%；当点阵结构最大长度为12 mm时，模型的最大位移为1.732 mm，最大数值出现在模型无约束的一端，与原模型的2.098 mm相比，刚度提升17.45%。模型的总质量为1.908 kg，比原模型减重20.5%；当点阵结构最大长度为14 mm时，模型的最大位移为1.558 mm，比原模型刚度提升25.74%。点阵拓扑优化后结构总质量为2.1 kg，比原模型减重13.33%。当点阵结构最大长度为16 mm时，模型的最大位移出现在远离约束的端部，其数值为1.239 mm，与原模型2.098 mm的变形相比，刚度提升40.94%。点阵优化后，结构的总质量为1.81 kg，比原模型减重了24.58%。当点阵结构最大长度为18 mm时，模型的最大位移为1.309 mm，与原模型的2.098 mm的变形量相比，模型整体的刚度提升37.61%。优化后的模型质量为2.43 kg，比原模型减重-1.25%。

图14 点阵结构不同最大长度下的位移变形云图

当点阵结构最大长度为20 mm时，模型的最大位移为1.274 mm，出现在模型无约束的一端。与原模型的2.098 mm相比，模型整体的刚度提升39.28%。优化后的点阵模型总质量为2.48 kg，比原模型减重-3.33%。

综上所述，不同点阵结构最大长度的对比结果如表1所示。从表1可以看出，随着点阵结构最大长度的增加，点阵结构的直径变化范围增大，能够快速进行刚度提升。在结构轻量化方面，较短的点阵有较大的优势，这是因为点阵较短，数量较大，存在更多的截面尺寸变化的自由度，能提供更多的减重选择。

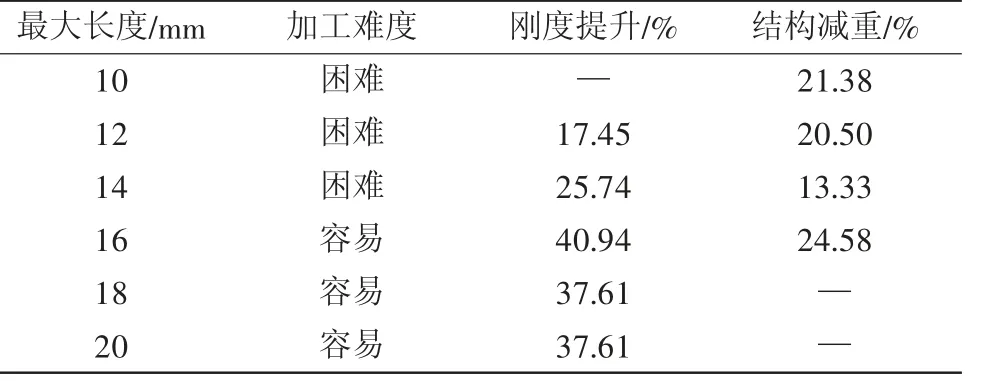
表1 不同点阵结构最大长度对比结果

同时从上述点阵拓扑优化结果中可以看出，如果不控制点阵直径的上限值，点阵优化结果的质量将逐渐增大。所以在本次优化中，人为约束点阵结构直径的范围为1～3 mm，对设计区域进行点阵优化。最终优化结果如图15所示，为了保证结构的轻量化，点阵结构直径的下限值为1 mm，结果表明点阵结构有着明显的梯度变化趋势。