航天服软关节小样本阻力矩预测方法研究
2022-08-26董长林周仕明李道奎
董长林,周仕明,李道奎*
(1.国防科技大学空天科学学院,长沙 410073;2.空天任务智能规划与仿真湖南省重点实验室,长沙 410073)
1 引言
舱外航天服是航天员出舱活动必须穿戴的个人防护装备。航天服充气后出现内外压差,导致作业过程中出现气体压缩和材料变形等现象,它们共同作用在关节处产生阻力矩,影响航天员的作业能力。因此,舱外航天服的关节阻力矩大小对软关节的灵活性和可靠性影响较大。由于航天员与不同结构、不同尺寸的航天服之间存在着不同的人-服耦合特性,因而阻力矩特性不同。考虑上述特性对航天服进行迭代与优化时,仿真和实验的成本高、效率低,故建立小样本阻力矩预测方法对航天服设计开发阶段具有重要意义。
航天服关节阻力矩特性研究大致包括关节阻力矩实验、有限元分析、理论计算和阻力矩预测4个研究阶段。早期研究主要采用实验方法。Vykukal等设计了一种航天服关节阻力矩外置法测量装置,为外置法实验的发展打下了基础。Matty提出了一种能够消除重力影响的水平面内的测量方法,在关节阻力矩实验中应用广泛。在此基础上,Meyen等针对航天服软关节进行了内置法实验,并测得内置法驱动的关节阻力矩。王晓东等进行了航天服上肢关节舱外作业的实验研究,发现关节阻力矩不仅具有迟滞特性,还具有历程特性。通过实验研究能够获得阻力矩特性,但成本高、效率低,在设计优化阶段难以穷举。
伴随计算机科学技术的发展,逐渐利用仿真分析进行关节阻力特性的研究,以降低成本。Furuya等进行了航天服圆筒关节模型和波纹管关节模型的弯曲仿真,并分析了弯曲过程中褶皱出现原因及其发展的过程。尚坤等针对航天服平褶式关节进行了有限元仿真,并通过能量法分析得知关节阻力矩是由气体压缩、材料变形及摩擦共同作用所导致。王鲁豫等开展了航天服波纹式髋关节仿真研究,并以关节阻力矩和压缩气体做功最小为目标进行了优化,提高了关节的灵活性和操作性。然而,对于复杂运动历程或考虑不同人-服耦合特性时,有限元方法的计算效率较低。
为解决上述问题,尝试采用理论方法求解航天服的关节阻力矩。Schmidt建立了航天服关节膜和梁的理论模型,并通过实验验证了航天服关节更符合膜简化模型,即关节阻力矩主要是由压缩气体做功引起的;然后基于膜模型建立了无人状态关节运动变形的解析模型,但由于体积计算存在误差且仅考虑压缩气体产生的阻力矩,导致该模型仅适用于小角度范围的关节转动。李广利等通过能量法推导了无人状态下波纹式关节的阻力矩方程,但其仅在弹性范围内适用,且难以考虑材料迟滞特性、厚度等因素的影响,与工程实际中的人-服耦合存在一定的误差。综上,现有的理论方法在变形假设和体积计算方面均存在误差,不适用于关节转角较大时的阻力矩计算;且难以开展人-服耦合特性分析,因而在工程中的应用受到很大限制。
鉴于理论方法的局限性,基于已有的实验和仿真成果,阻力矩预测模型方面的研究逐步开展,以提高复杂运动历程下关节阻力矩的求解效率。Schmidt首先引入Preisach模型实现了对时间历程下航天服关节阻力矩的预测,且精度较高。后续研究不断针对Preisach模型进行改进和优化,以提高关节阻力矩的预测精度:文剑通过BP神经网络建立了基于Preisach模型的关节阻力矩预测模型,取得了较高的模型预测精度,但模型所需数据量较大且训练时间长;念龙生等提出了一种基于Preisach模型的内插方法,刘文樵将该方法应用于航天服关节阻力矩预测,取得了较好的预测精度。另外,也有部分学者尝试将不同方法或模型应用于航天服关节阻力矩的研究:王昊等、赵京东等通过外置法实验测得航天服关节阻力矩,并通过样条曲线对实验数据进行了拟合,但难以进行高精度的外插和预测;张新军等采用电磁学领域的Jiles-Atherton迟滞模型,通过遗传算法进行了参数辨识,进而对单历程阻力矩进行了拟合,但由于模型本身的对称性,拟合效果并不理想,因此该模型在航天服关节阻力矩领域的应用存在局限。可见,相对于其他方法,Preisach模型能够较好地表征关节阻力矩的迟滞特性和历程特性,但仍需要大量的实验数据才能准确预测关节阻力矩,否则预测结果会出现较大误差。
综上所述,为改善Preisach模型对数据样本的依赖性,本文深入分析Preisach模型在小样本条件下预测误差产生的原因,并对该模型进行修正;进一步,针对修正后的模型推导由于样本减小而产生的预测误差,进而提出小样本条件下的阻力矩预测方法,并对该方法进行验证。
2 基于Preisach模型的阻力矩预测误差分析与修正
2.1 Preisach模型
在航天服关节弯曲伸展过程中,由于气体做功、材料变形等因素影响,关节阻力矩在单历程运动中具有明显的迟滞特性,且在复杂历程运动中具有历程相关性。Preisach模型作为基于唯象学方法的迟滞模型预测方法,能够考虑历程特性用于航天服关节阻力矩的预测。Preisach模型将阻力矩曲线转换为另一平面的积分形式描述,该模型数学描述如公式(1)所示:
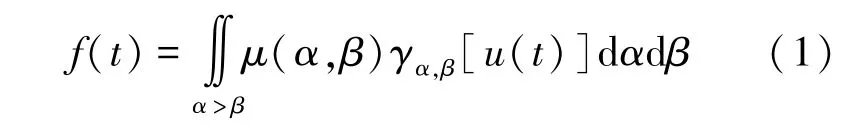
式中,()是时刻关节阻力矩大小。(,)是迟滞函数。()是时刻输入转角大小,以划分正、负积分平面,定义正、负积分区域分别为、,如图1所示。γ[()]为基于关节转角()的符号函数,在正向区域为+1,在负向区域为-1。基于()对积分平面分割和γ[()]的正负性,利用积分区域变换性质将式(1)整理为式(2)。
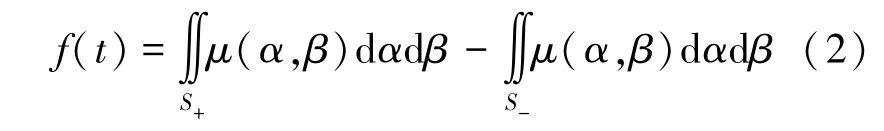
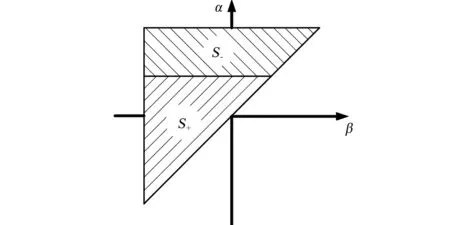
图1 预测模型积分平面Fig.1 Integral plane of the prediction model
定义整个积分平面为,则有整个积分平面内均为正积分时的积分值为。根据运动历程转角变化情况对积分平面的分割,可将式(2)转换为正积分或者负积分的表述形式,如式(3)所示。
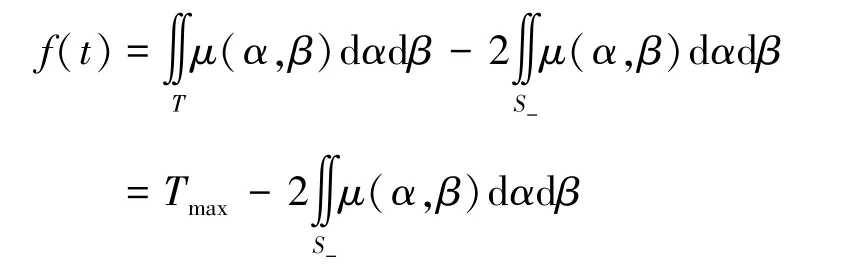

关节复杂运动历程对应积分平面的变化情况如图2(a)所示。根据积分平面变化情况将历程曲线划分为3段:①段关节转角增加,随关节转角增加水平边界上移,使得积分区域变化;②段为关节转角加载到极值点后卸载过程,在积分平面斜边边界处增加竖直边界,随关节转角减小竖直边界左移改变积分区域;③段为卸载到极小值后再加载过程,在积分平面斜边边界处增加另一水平边界,随转角增大水平边界上移,改变正负积分区域。同上述方法,关节转角历程转化为正负积分区域的变化,正负积分区域边界拐点对应关节加载卸载历程中极值点,如图2(b)所示。因此,该方法可以记录关节运动历程对现有关节阻力矩的影响,即模型能够考虑关节运动的历程特性。
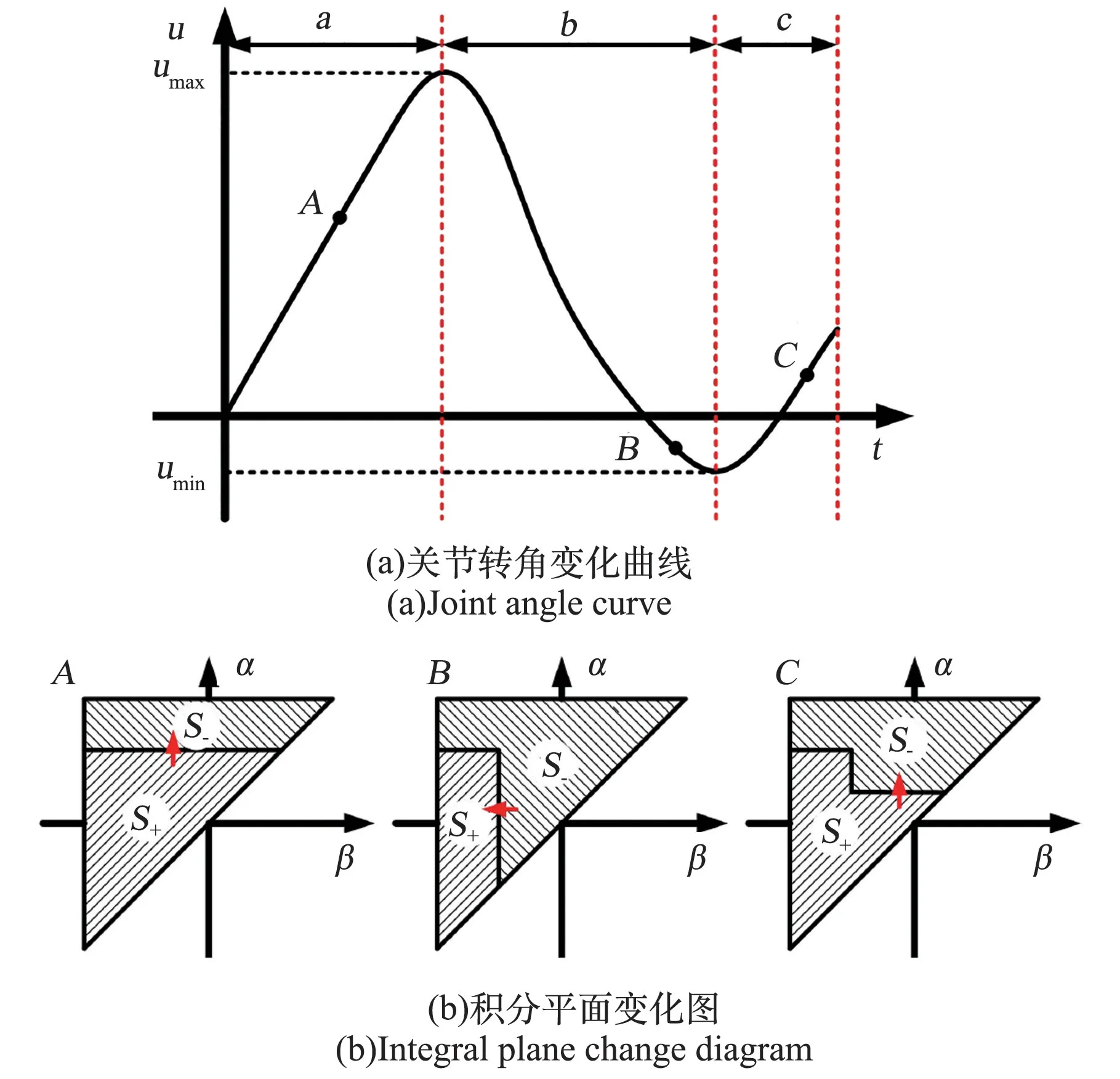
图2 加卸载历程对积分平面分割Fig.2 Influence of loading and unloading process on integral plane segmentation
当关节运动历程为单历程加载卸载时,关节阻力矩及积分面变化如图3所示,定义(α,β)为转角先加载至α再卸载至β对应阻力矩变化值,可以得到加载至α再卸载至β时阻力矩差值与积分区域的关系如式(4)所示。

图3 加卸载阻力矩变化对应面积分变化关系Fig.3 Relationship between change of loading and unloading resistance torque and change of area fraction
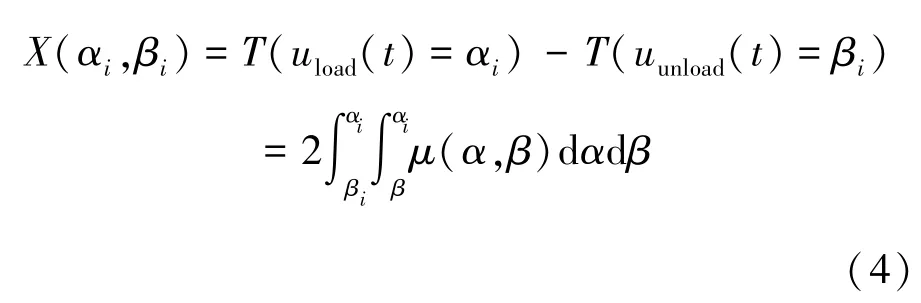
由图3可通过关节单历程运动将整个积分平面离散化,即通过积分几何意义描述。同理,可将式(1)微分,通过迟滞函数对积分平面进行表征,迟滞函数的微分形式如式(5)所示:

Preisach模型是一种唯象学模型,若采用式(5)通过迟滞函数连续描述积分平面,由于含微分项,受实验数据噪声影响会导致迟滞函数和积分后阻力矩预测产生较大误差。因此,本文采用积分几何意义的方法对积分平面进行表征。
基于航天服关节单历程加卸载过程,阻力矩差值对应图4中红色卸载区域面积分积分值的2倍,通过每次加载至极值点α后卸载,将数据点离散可对应多个β值。因此,可以根据输入数据将整个积分平面离散为不同α和β,如图4所示。
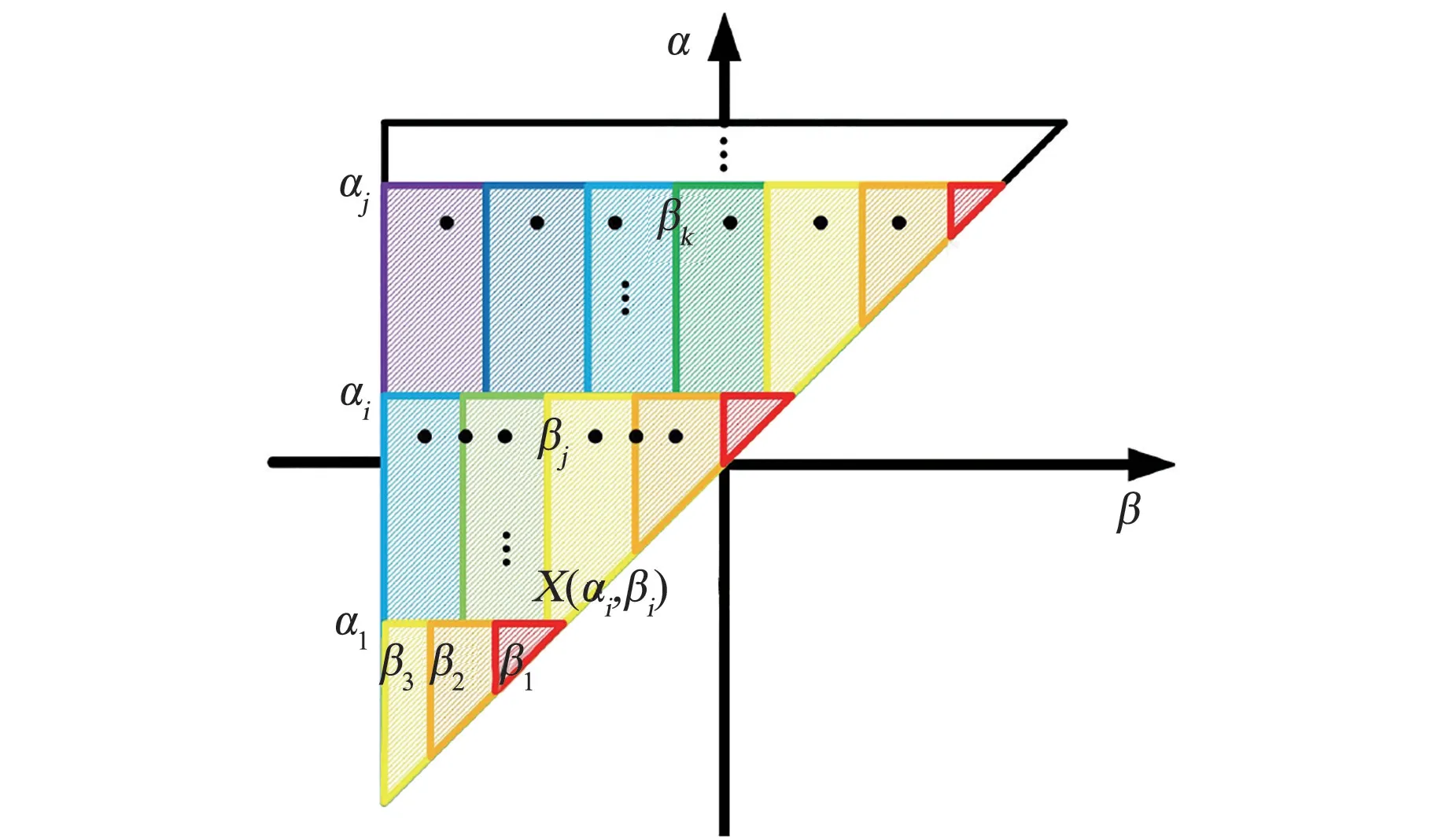
图4 积分平面离散图Fig.4 Integral plane discretization diagram
基于上述离散方法可以将整个积分平面离散为(α,β)形式,因此针对任意给定积分区域范围,如图5所示,其正积分区域积分值可表述为式(6)。
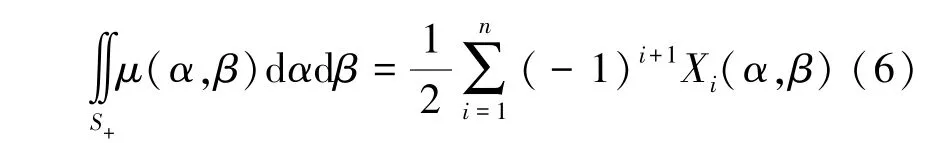

图5 积分平面分解图Fig.5 Diagram of integral plane decomposition
将式(6)带入式(3),整理得到任意历程下关节阻力矩计算公式,如式(7)所示。
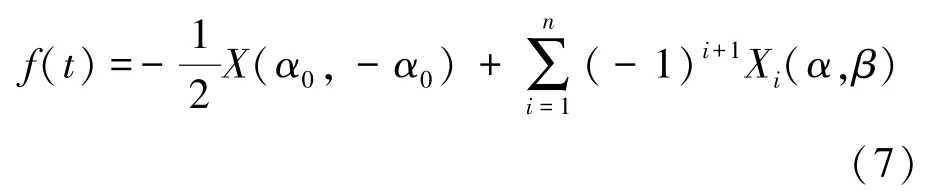
2.2 Preisach模型预测误差分析
为了将积分平面准确对应于离散的积分点,需要大量实验数据将积分平面进行离散,因此样本数会对积分平面表征精度产生影响。但由于预测点并不一定落在给定数据上,对预测点的面积分可以采用不同的内部插值方式进行计算,本文以精度高、参数少的权重系数法为例,对样本减小所引起的模型预测误差展开分析。
积分区域由=,=-,=作为边界构成,因此不同运动历程对应阻力矩预测可分为3点预测和4点预测。3点预测对应在=边界附近的预测值,4点预测则对应远离=边界的预测值,如图6所示。

图6 基于临近点预测示意图Fig.6 Schematic diagram based on near point prediction
基于临近点预测,小样本较大样本条件下,临近点数据位置发生移动,样本减小后对同一点的预测如图7所示。

图7 数据点减少临近点预测示意图Fig.7 Schematic diagram based on near point prediction with data reduction
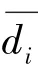

则有对任意预测点的计算方法如式(9)所示。
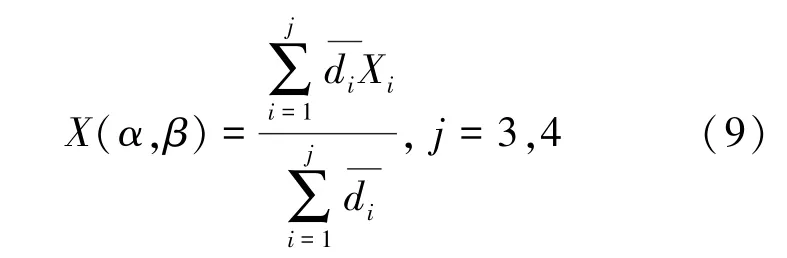
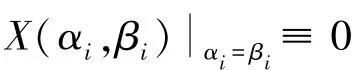
采用单历程加卸载最大转角分别为20°,40°,60°共3组数据对肘关节复杂运动历程进行预测的结果,如图8所示。图8(a)中段为航天服内部充气阶段;段为关节初始运动阶段;段关节进行特征性运动,阻力矩随关节运动变化;段关节运动停止,阻力矩基本保持不变。段、段与段为非预测段,段能够反映关节复杂运动过程中阻力矩特性,为预测研究段。由图8(d)可知,预测范围内在极值点附近预测误差较非极值附近预测误差明显增大,且该预测误差对极值点后续预测产生影响,验证上述分析正确性。
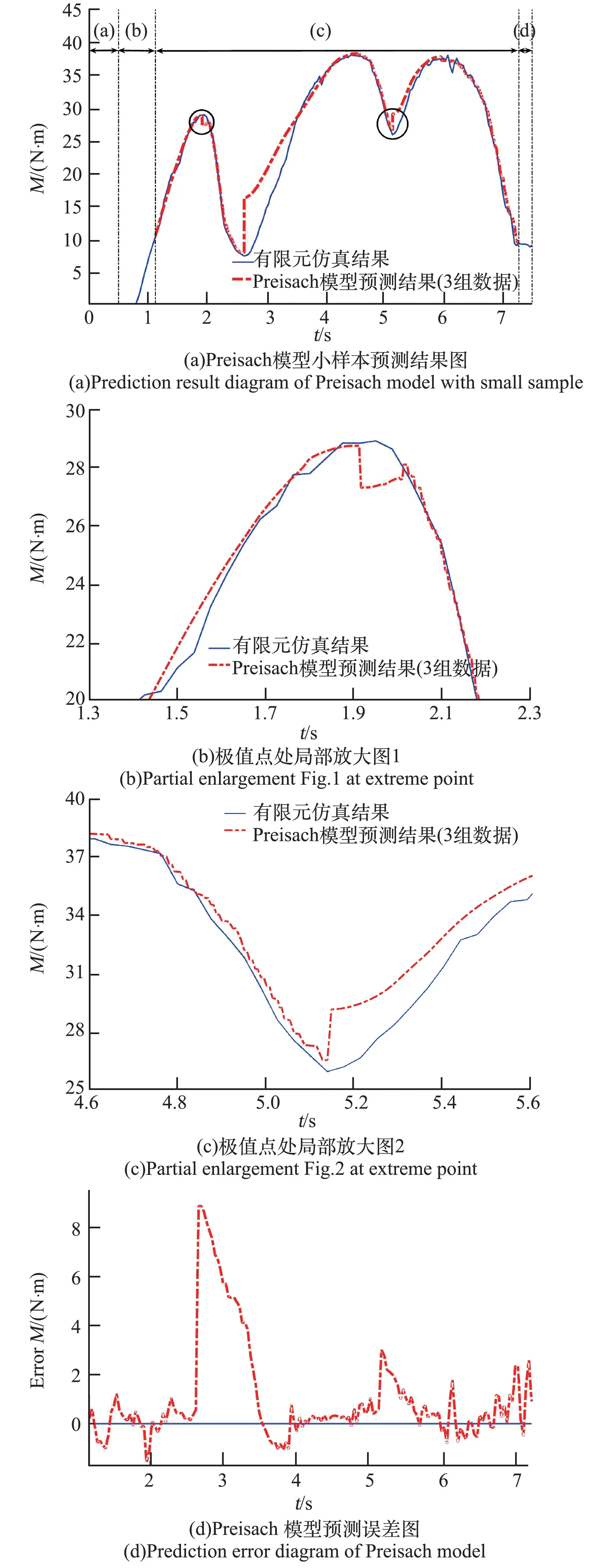
图8 3组输入数据预测结果Fig.8 Prediction results of 3 groups of input data
2.3 Preisach模型预测误差修正
由于在积分平面边界=较非边界处样本减小引起的误差较大,且模型的历程特性会导致极值点的预测误差对后续产生影响,因此主要针对该边界处进行修正。
式(5)中采用迟滞函数微分方式表征积分平面,由于迟滞函数误差会导致阻力矩预测误差,故采用积分几何意义对积分平面离散,通过权重系数法进行预测点面积分的计算。在小样本条件下,数据点偏移较大导致临近点中非零项权重变化,产生极值点处的预测误差。
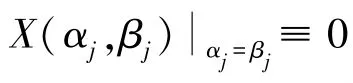

图9 边界附近预测点积分平面修正Fig.9 Integral plane correction of prediction points nears boundary
模型修正后,同样采用上述3组数据进行预测,结果如图10所示。修正后预测曲线较未修正预测曲线在极值点处能够一定程度降低模型的预测误差,但关节阻力矩仍存在较大误差。在阻力矩最大值附近未出现较大预测误差,这是由于输入数据含60°单历程迟滞曲线临近最大阻力矩对应关节转角。
由图10可知,采用同样的输入数据对复杂运动历程进行预测,模型修正后能够明显提高极值点附近的预测精度。但在数据较少时,积分平面表征精度不足,使得预测点积分值计算不准确,预测结果在极值点附近仍存在明显误差。因此,有必要针对修正后模型作进一步分析。
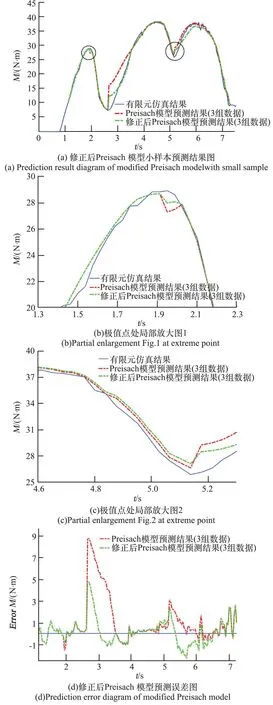
图10 积分平面修正后3组输入数据预测结果Fig.10 Prediction results of 3 groups of input data after integral plane correction
3 小样本阻力矩预测方法
3.1 小样本预测误差的分析
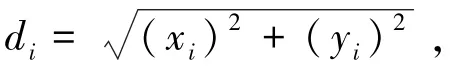
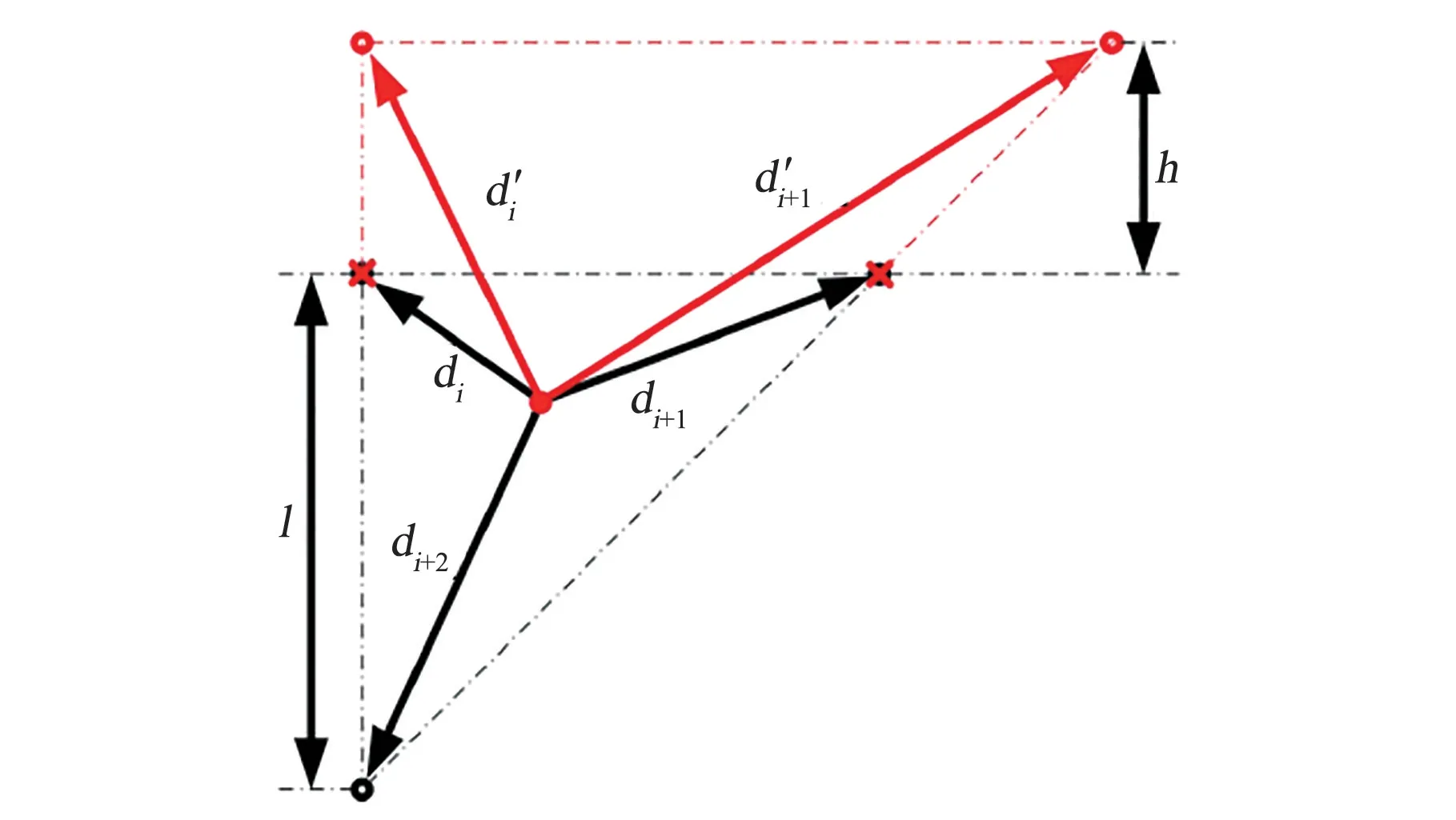
图11 数据减少导致积分区域变化Fig.11 Changes of integral area due to the decrease of data
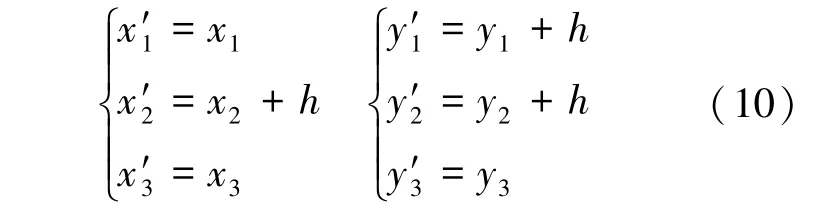
基于式(4),偏移后临近非零点的面积分′,通过积分几何意义可表述为式(11)。



考虑到由于数据减少带来的偏移远大于临近范围预测尺寸,则有式(13)所示。
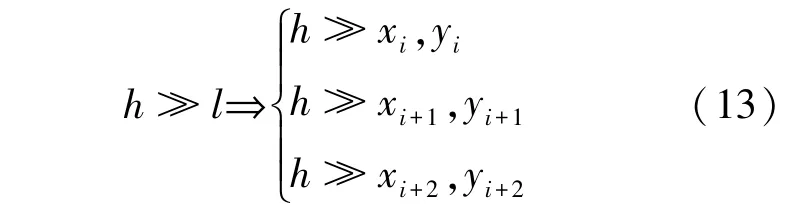
针对Δ可以分为前一部分的高次项和后部分的常数项,主要针对高次项展开分析。略去其中小量,可简化为式(14)。
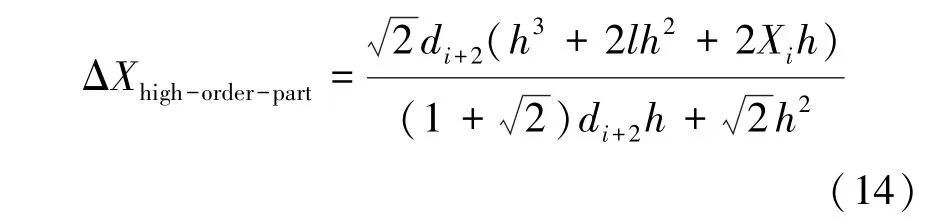
预测点面积分的预测误差Δ,主要由数据减少产生的偏移量和d共同决定。由于数据点减少导致模型预测误差随着偏移量的增加而显著增大,与上述分析结果符合。即输入数据中,极值点较非极值点附近单历程迟滞曲线对积分平面表征贡献性更大。
3.2 极值点法的小样本阻力矩预测方法
基于上述对阻力矩预测模型误差的研究,在关节复杂运动预测过程中,小样本条件下积分平面边界=处权重变化,使得极值点处误差较非边界处的误差更大。在此基础上针对极值点处积分平面进行修正,虽然能在一定程度上降低预测误差,但修正后模型在极值点附近由于数据点减少而导致模型的预测误差仍然存在,误差随数据减少引起的偏移量增加而明显增加。
3.1节推导了在小样本下数据点减少引起的模型预测误差,确定了预测精度主要由输入数据远离极值点的距离而决定,即极值点附近数据较非极值点数据对模型预测精度影响(对积分平面表征贡献)更大,基于此提出极值点法的小样本阻力矩预测方法。由于最大误差位置出现在关节运动过程极值点处,且对后续预测存在影响,因此主要考虑误差较大的极值点附近对预测的影响,对输入数据进行限制能够明显降低输入数据数量的同时提高预测精度。输入数据以关节可能运动过程中主要动作或重复性动作为依据,确定运动历程,提取关节运动过程中的极值点,对临近极值点合并以减小输入样本大小;对于非极值点的单历程数据,以能够提高积分平面表征精度为依据,增加其他有效数据点,依据图4,提高模型的拓展修正性。以单历程运动阻力矩-转角迟滞特性曲线作为输入,同时对边界附近积分平面进行修正,实现对关节复杂运动历程阻力矩的预测。采用极值点法输入3组数据对任意复杂运动历程阻力矩的预测结果如图12所示。
图12中红色点划线为极值点法预测结果,较原模型方法预测结果,最大预测误差由8.881 Nm降低至2.565 Nm,最大预测误差明显降低。采用极值点法能够在满足预测精度要求的前提下,显著降低样本数量。
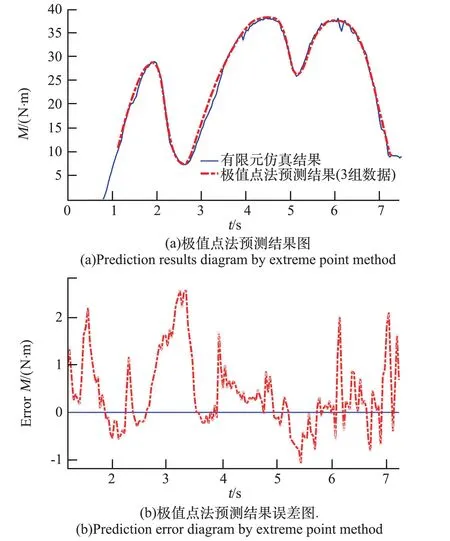
图12 3组输入数据极值点法预测结果及误差图Fig.12 Prediction results and prediction error of extreme point method for 3 groups of input data
输入3组数据采用极值点法预测时,能够显著降低在极值点处的预测误差。但图中3.15 s附近由于该部分较各输入数据偏移较大,导致该部分积分平面表征存在误差(可通过对积分平面表征不准确处补充数据,以达到提高精度的目的),因此预测误差较大,但较原模型误差仍有明显减小。这是由于在非积分边界处的4点预测较3点预测方法受权重变化造成的影响更小,与2.2节分析相一致,因此极值点法能够在小样本条件下保证预测精度。
4 航天服软关节小样本阻力矩预测验证
4.1 航天服典型关节运动历程
航天服肘关节作为上肢作业时主要参与关节,同时肘关节多采用波纹式结构以降低关节弯曲时压缩体积所引起的阻力矩,因此本文以波纹式肘关节为研究对象针对关节阻力矩的小样本预测方法进行验证。按照波纹式关节提取单元模型相关参数如图13所示。
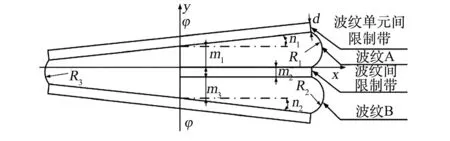
图13 波纹式肘关节单元结构参数示意图Fig.13 Schematic diagram of structural parameters of corrugated elbow joint unit
上述确定航天服波纹式肘关节结构,根据GJB 36A-2008《飞行员人体模板设计和使用要求》建立170 cm人体大臂、小臂关节人体模型,以此为人-服耦合模型研究对象。以单历程加卸载过程关节阻力矩随转角变化的迟滞特性曲线作为预测模型的输入数据,如图14所示,用于预测复杂运动历程下关节阻力矩变化情况。

图14 单历程关节阻力矩-转角迟滞特性曲线Fig.14 Resistance torque-angle hysteresis characteristic curve of single path joint
开始时,航天服与人体处于初始状态并进行充气;充气完成后,航天服采用内置法人体驱动方式运动,肘关节转动至12.9°时,人体与航天服刚产生接触;按照图14中蓝色实线关节弯曲加载至转动最大角度,阻力矩增加;而后按照红色点划线关节伸展卸载至初始状态,阻力矩减小。加卸载曲线不重合,阻力矩在关节加载、卸载过程呈现明显迟滞特性。在之前的研究中,通过实验验证了有限元仿真分析方法的正确性和有效性,因此以仿真数据代替实验进行验证。
任取航天服关节运动历程,如图15所示。将关节运动历程分为3段:段由于人体与航天服从未接触状态转变为刚产生接触,航天服开始产生体积压缩和材料弹性变形等,作用于关节产生阻力矩;段人体关节持续运动与航天服接触,阻力矩随关节运动变化;段关节停止运动,直至仿真分析结束。段人服刚接触,关节阻力矩较小、段关节保持不动至计算结束,阻力矩基本保持不变。因此以段关节运动为预测段进行关节阻力矩预测,即以图15中黑色实线展开研究。
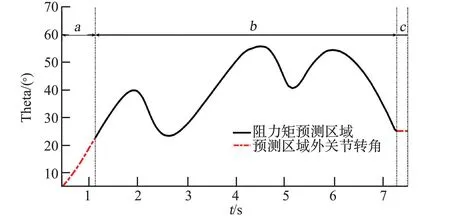
图15 关节运动历程曲线Fig.15 Motion history curve of the joint
由于航天服关节阻力矩具有迟滞特性与历程相关性,预测段曲线具有加载段和卸载段能够反应阻力矩的迟滞特性;且该段曲线存在卸载后过加载以及卸载后非过加载后卸载过程,能够充分体现运动加载历程对关节阻力矩产生的影响。因此该曲线能够特征明确地反映关节运动过程中可能存在的特性,故选用该曲线作为复杂运动历程特征曲线进行关节阻力矩预测。
4.2 航天服关节阻力矩预测结果分析
在给定范围内分别采用均匀取点方式与极值点法2种方式进行预测,结果如图16所示。图16中黑色实线为仿真分析结果关节阻力矩随时间变化曲线、红色点划线为基于Preisach模型小样本下阻力矩预测结果、绿色点划线为修正后Preisach模型阻力矩预测结果、蓝色点划线为采用极值点法在相同数据量下阻力矩预测结果。分别输入3、5、7组数据,预测结果如图16(a)~(c)所示,预测结果方差见表1。
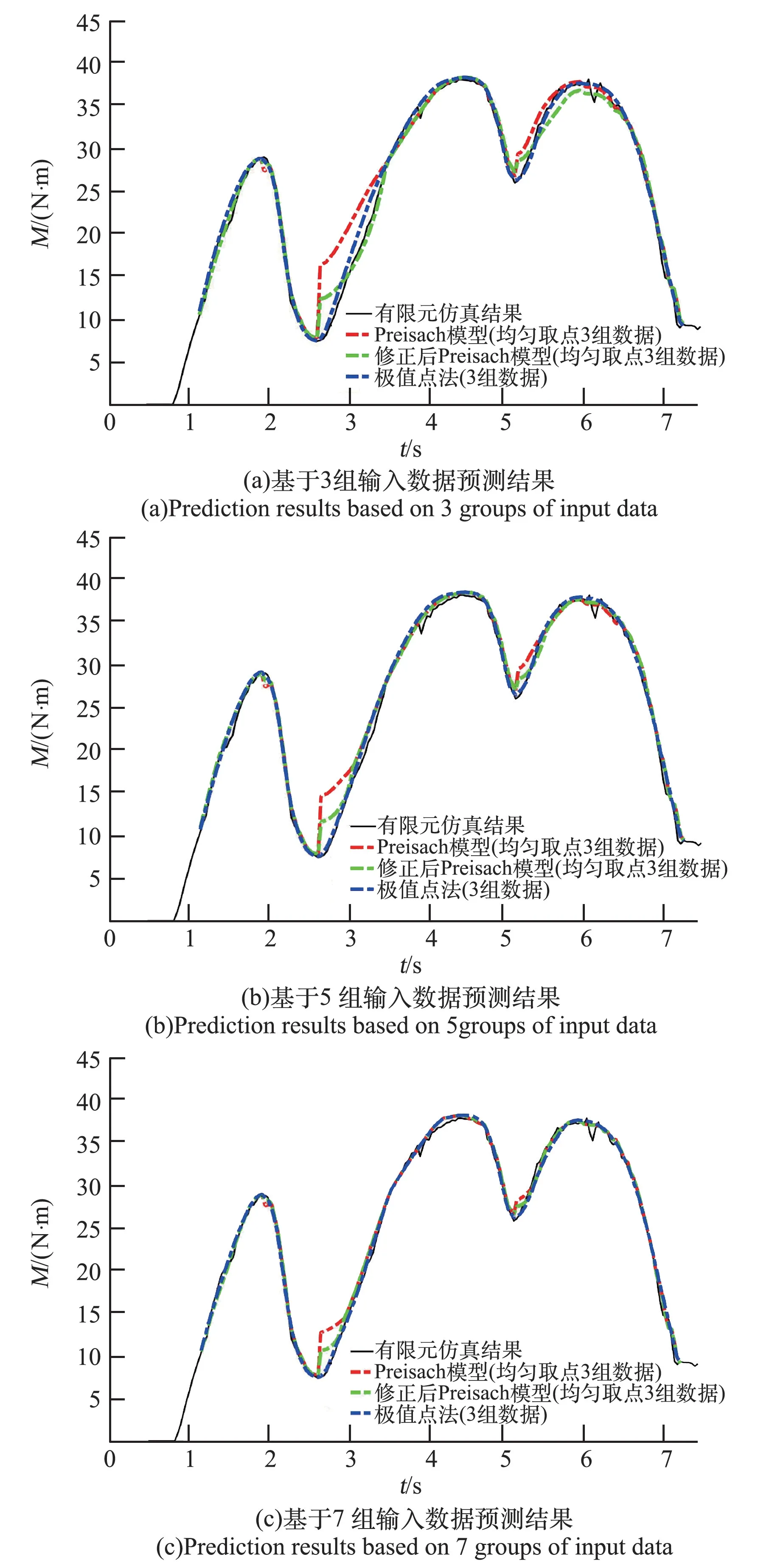
图16 不同组数据预测结果Fig.16 Prediction results of different groups of data

表1 不同方法模型预测误差Table 1 Prediction error of different methods
通过验证,采用极值点法能够明显降低对实验数据数量的需求,并提高模型的预测精度;较Preisach模型及修正后的Preisach模型均匀取点方法精度明显提升,且能够避免局部较大误差。验证了该方法的有效性和正确性。
输入不同组数数据时,采用极值点法对关节阻力矩进行预测,结果如图17所示,预测误差见表1。
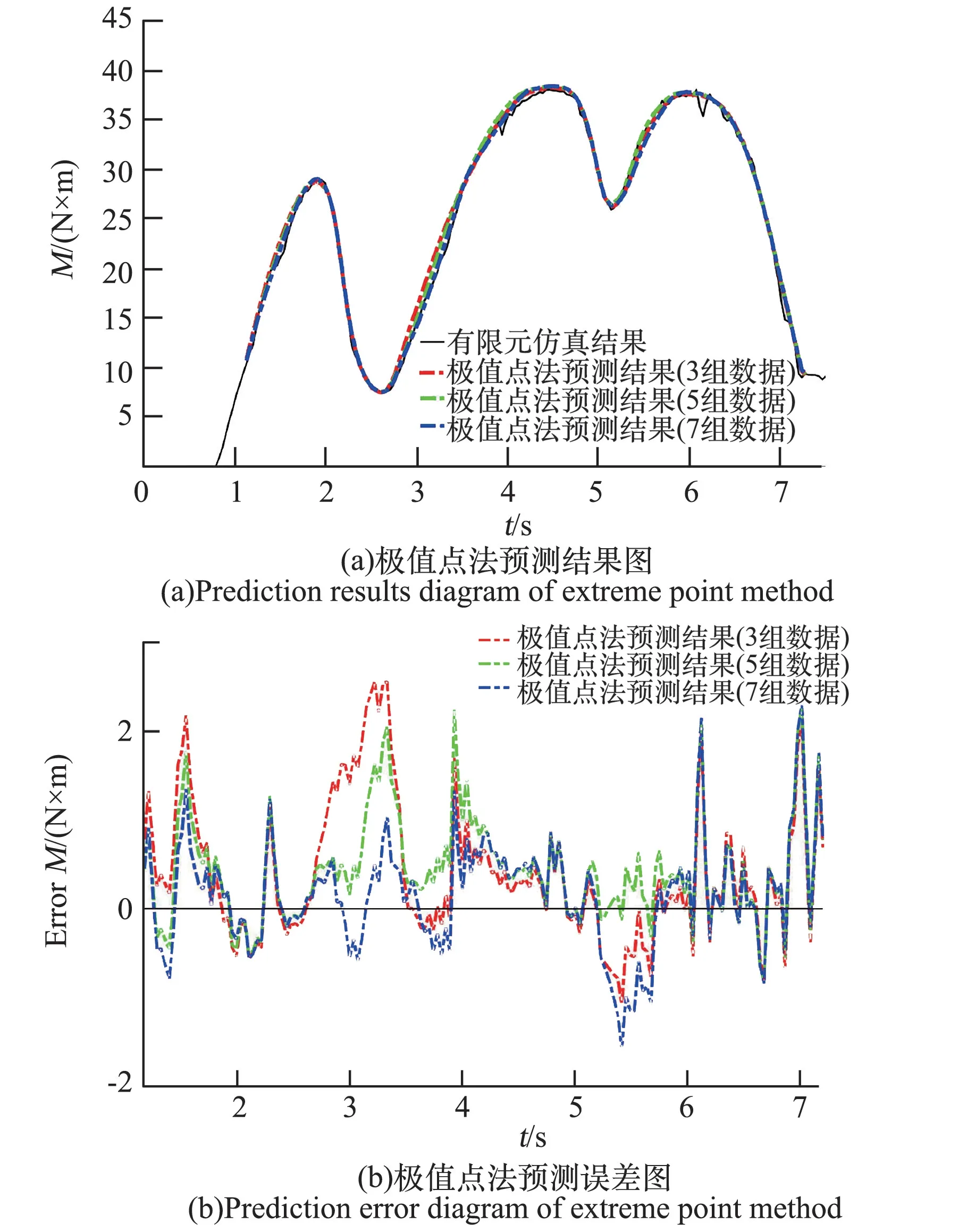
图17 不同组输入数据输入模型预测结果Fig.17 Prediction results of the model for different groups of input data
由于通过积分几何意义对积分平面进行表征,采用内插方式确定预测点积分值,随输入有效数据组数增加,离散数据能够更精确的表征积分平面的变化,使预测误差降低,因此该方法能够随有效数据增加进行拓展修正。同时,该方法能够在小样本条件下,达到较高的精度要求。对试验及仿真时测试点的选取具有指导意义。
5 结论
本文分析了Preisach模型预测误差产生的原因,修正了模型的积分平面,推导了数据减少引起的预测误差,并基于此提出了极值点法的航天服软关节小样本阻力矩预测方法,该方法能够在保证模型预测精度条件下显著降低对数据量的需求。主要结论如下:
1)从Preisach模型预测原理出发,对小样本阻力矩预测时产生局部较大误差的现象进行了分析,得到了误差产生是数据点权重系数变化所导致。
2)基于阻力矩预测模型原理和误差分析,利用积分平面性质,对Preisach模型预测过程进行了修正,降低了权重系数变化产生的影响,减小了预测误差。
3)推导了小样本下数据较少所引起的预测误差,提出了极值点法的小样本阻力矩预测方法,显著降低了对数据量的需求并提高了预测精度,且该方法能随有效数据的增加进行拓展修正。
