基于CEEMD和排列熵的矿山微震信号降噪研究

2022-08-25田全虎王英乐郑禄林刘子琪

黄金 2022年8期

田全虎，王英乐，郑禄林,3*，刘子琪

(1.贵州锦丰矿业有限公司； 2.贵州大学矿业学院； 3.厦门大学建筑与土木工程学院)

引言

微震监测是针对矿山岩爆、矿震等灾害的一种区域性监测技术，可以监测到岩体内部的破裂情况，对矿山安全生产具有重要的参考作用[1-2]。但是，实际生产过程中的环境复杂，微震监测系统采集到的微震信号受到复杂的背景噪声干扰。因此，如何将无效的噪声信号滤除，提取出有效的微震信号，具有重要的研究意义。

微震信号是典型的非线性、非平稳信号，传统的傅里叶变换降噪可以在一定程度上去除噪声，但是该方法更适用于处理平稳的周期性信号，对微震信号这类含有突变的信号降噪效果不理想[3]。目前，常采用的非线性信号降噪方法有经验模态分解(Empirical Mode Decomposition，EMD)[4]和小波降噪[5]等。小波降噪虽然具有较好的分辨特性，但需要选取适合降噪信号的基波函数和阈值才能较好地对信号去噪，而且不同的基波函数适应性也不同；EMD自适应分解降噪虽然有一定的优势，但是其分解算法的不稳定性和模态混叠现象的存在，使得该方法具有很大的弊端[6]；集合经验模态分解(Ensemble Empirical Mode Decomposition,EEMD)通过加入噪声对EMD进行了改进，虽然抑制了一定程度的模态混叠效应，但其计算量较大、信号内部的不同频率分量分割效果不理想。

YEH等[7]提出互补集合经验模态分解(Complementary Ensemble Empirical Mode Decomposition，CEEMD),该算法通过在原始信号中添加幅值相反的两对白噪声后，对其分别进行EMD分解，最后再将分解结果组合得到不同频率的本征模态函数(IMF)。CEEMD算法不仅保证了分解效果，而且还抑制了由于添加了白噪声而造成的重构分量误差。排列熵(Permutation Entropy，PE)是一种检测时间信号序列的随机特性和动力学突变的算法，该算法抗干扰能力强且计算速度快，可以作为检测信号序列中所含随机噪声程度的一种定量指标[8]。

针对EMD、EEMD等[9-11]方法存在的缺陷，为较好地剔除微震信号中的噪声成分，本文提出将CEEMD分解与排列熵算法相结合的降噪方法，通过CEEMD将微震信号分解为数个IMF分量，计算每个IMF分量的排列熵值，根据该值的大小判断IMF分量的随机性程度并筛选出需要去噪的分量，最后利用小波阈值降噪对筛选出的分量进行滤波降噪。通过仿真信号和微震信号实例分析，表明该方法可以适应微震信号分析处理，能够更好地将微震信号中的随机噪声滤除，减少噪声信号的干扰并且提取出有用信号成分。

1 基本理论

1.1 CEEMD算法

CEEMD算法是针对EMD算法存在的模态混叠和端点效应等问题而提出的改进信号分析方法，适用于处理非线性、非平稳信号的分解和降噪问题。该算法消除了EEMD算法中白噪声对原始信号的影响。在分解时采用相对较少的集合平均次数，不仅可以极大地降低剩余噪声干扰，而且能节省计算时间。CEEMD算法流程如下：

1)在原始信号中加入一组正负互为相反的噪声信号，加入新噪声信号的幅值相等，如式(1)、式(2)所示，且求解出加噪信号的EMD分解结果，直到筛选信号结束。

(1)

(2)

3)求出IMF1与IMF2的集合平均值，即为分解最终结果。其中，添加的白噪声对最终分解结果的影响符合以下条件：

(3)

(4)

式中：γn为最终误差的标准差；l为加入噪声的次数；e为加入噪声的幅值。

本文选择0.2倍原始信号作为加入噪声的幅值，分解平均次数为200次。

1.2 排列熵算法原理

排列熵算法是由BANDT等[12]提出的一种检测时间序列和动力学突变特征的算法。PE算法的概念简单，数据计算速度快，而且抗干扰能力强，因此其非常适用于非线性信号的分析处理，具有较好的鲁棒性。其计算流程如下:

X(i)是长度为N的时间信号序列，对该信号进行相空间重构，可以得到如下信号序列：

(5)

式中：m为信号序列嵌入的维数；λ为信号的时间延迟。

将X(i)的m个向量：X(i)=(x(i),x(i+λ),…,x(i+(m-1)λ))从低到高排列，得到一组新的信号序列：S(g)=[j1,j2,…,jm]，其中，g=1,2,…,k,k≤m!。由于共有m!种不同的信号序列，S(g)是m!种信号序列的一种，因此计算每种信号序列出现的概率为：p1,p2,…,pk。

时间信号序列X(i)的排列熵(Hp(m))定义为：

(6)

Hp=Hp(m)/ln (m!)

(7)

经过归一化处理后的Hp值为[0,1]，其数值表示信号序列的随机性程度，该值越大,表明信号序列的随机性越强;否则该信号序列越平稳规则。

1.3 降噪效果评价原则

原始信号经过降噪处理后，为判断信号的去噪效果是否有效，可以通过观察信号的频谱图进行主观评判。为通过定量标准来判断分析信号的去噪效果，本文选取应用广泛的信噪比(SNR)和标准差(RMSE)等参数对信号的去噪效果定量表征。

定义Y(n)为原始带噪信号，y(n)为去噪后的信号。该信号的信噪比(SNR)越大，表示去噪效果越好，其定义为：

(8)

标准差(RMSE)的值越小，表示原始信号的去噪效果越明显，其定义为：

(9)

通过上述2种参数结合使用，可以定量反映出信号的去噪效果，能更好对比分析不同去噪算法的优劣。

2 微震信号降噪方法

矿山微震信号包含有丰富的岩体内部信息，由于现场监测环境复杂，岩体传播介质复杂，微震信号极易受到其他噪声信号的干扰。为去除微震信号中的高频噪声，保留有效的微震信号信息，本文采用CEEMD和排列熵算法对微震信号进行分解降噪。首先，采用CEEMD将原始微震信号分解为数个IMF分量；然后，计算每个IMF分量的排列熵值，根据排列熵值定量表征每个IMF分量所含随机噪声的程度，对含噪声较多的高频分量进行小波阈值降噪；最后，将去噪后的IMF分量与未进行去噪处理的IMF组合重构得到降噪后的微震信号。其具体降噪流程如下：

1)对原始信号x(t)进行CEEMD分解，得到数个IMF分量。

2)计算每个IMF分量的排列熵值，选定所含噪声较多的IMF分量。

3)根据需要降噪的IMF分量选定合适的小波降噪阈值，并对2)中选出的含噪声较多的IMF分量降噪。

4)将3)中降噪后的IMF分量和未进行降噪的IMF分量进行重构，可得降噪后的信号：

式中：y(t)为降噪后的微震信号；IMFi′(t)为经过小波阈值降噪的分量；IMFi(t)是未进行降噪处理的分量；r(t)为残余分量。

3 仿真信号分析

为验证本文所提出的基于CEEMD和排列熵的微震信号降噪方法对含噪信号的降噪效果，设计了一个仿真信号x(t)，该信号由正弦信号x1(t)和余弦信号x2(t)组成，且计算公式为：

(11)

式中：取t=[0,3]，且每间隔0.001 s采样一个点；n(t)为在原始信号中随机添加的高斯白噪声。

仿真信号x(t)的时域波形图和频谱图如图1所示。

图1 仿真信号时域波形和频谱图

为验证CEEMD的优越性，针对以上仿真信号，对其分别进行CEEMD和EMD分解，分解结果分别为IMF分量波形图和对应的频谱图，如图2和图3所示。由于图1中的原始信号混合有高频噪声，其频谱图中的高频部分明显。由图2、图3可知：仿真信号经过EMD分解和CEEMD分解后，分别得到9个和10个IMF分量及1个残余分量。其中，EMD分解存在一定程度的模态混叠和过分解现象，尤其是在IMF2、IMF3、IMF4和IMF5分量中模态混叠更加明显，高频成分和低频成分没有被充分分解，而且两类成分相互混叠对去噪结果有较大影响。相比之下，CEEMD分解方式可以较好地解决该问题，各IMF分量中没有明显的模态混叠。

分别计算CEEMD分解后的IMF分量的排列熵值，如表1所示。由于排列熵值的大小反映信号序列的随机程度，表1中的排列熵值表明，随着IMF分量分解阶次的增加，其随机性逐渐减小，因此仿真信号的噪声成分主要集中在前几个IMF分量中。根据表1中各IMF分量排列熵值的分布特点，本文选取排列熵值大于0.7的IMF分量进行小波阈值降噪。为对比分析本文所提降噪方法的优势，另外采用EMD分解降噪法和CEEMD分解剔除前2个IMF分量降噪法对仿真信号降噪处理。仿真信号经过3种降噪方法降噪后的效果如图4所示。为定量评价每种降噪方法的降噪效果，统计了3种方法对仿真信号处理前后的信噪比，结果如表2所示。

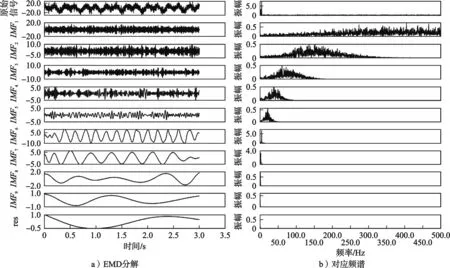
图2 仿真信号EMD分解结果

表1 CEEMD分解各IMF分量排列熵值

图4 仿真信号3种方法降噪效果对比

表2 3种降噪方法降噪效果对比

结合图4降噪后的仿真信号波形和表2降噪后的信噪比分析可知：

1)经过EMD降噪后的仿真信号失真相对严重，波形不够光滑，受噪声影响明显，其信噪比最低，为12.673 1 dB。

2)经过CEEMD分解并剔除前2个IMF分量的降噪方法处理后，仿真信号中的高频噪声大部分被剔除，波形相对EMD方法更平整光滑，其信噪比也有所提高，为15.873 2 dB。

3)本文提出的基于CEEMD和排列熵的降噪方法对比前二者降噪效果最好，信噪比最高，达到21.654 8 dB，而且波形得到了更为准确的还原，波形曲线更加光滑。

以上仿真信号试验表明：基于CEEMD和排列熵的降噪方法可以对信号进行有效降噪，相比单独使用EMD和CEEMD方法降噪，该方法得到的降噪效果更加准确，而且该过程具有自适应的处理特点，在实际应用中可以提高微震信号的处理效率，节省时间。

4 工程应用实例

4.1 工程背景

贵州锦丰矿业有限公司(下称“锦丰金矿”)位于贵州省黔西南自治州贞丰县内，矿区位于北盘江与洛凡河分水岭地带，矿体赋存于三叠系碎屑岩弱含水岩组中，且由于黏土岩发育，破碎带蚀变严重。矿体及顶底板围岩以薄至中厚层砂岩与薄层黏土岩为主，地质构造发育，风化作用强烈，黏土岩软弱层及断裂破碎带影响岩体稳定，易发生垮塌，属工程地质条件中等的半坚硬软弱层状碎屑岩类矿床。因此，在该矿山建立了一套IMS微震监测系统，用于研究该矿山巷道开挖影响下的岩体稳定性。从该系统中选取3组典型微震信号，通过MATLAB平台对其采用基于CEEMD和排列熵的降噪方法进行处理分析。

4.2 降噪效果分析

对选取的3组微震信号采用基于CEEMD和排列熵的降噪方法进行处理分析，其降噪前后的波形图和频谱图如图5所示。

图5 微震信号降噪效果

由图5可知：3组原始微震信号通常会受到高频噪声影响，其频谱图中200～500 Hz部分高频分量明显，很大程度上影响真实微震信号波形分布。经过CEEMD和排列熵降噪处理后，3组原始微震信号中的高频分量均被有效滤除，降噪后的波形相对更加完整、平滑，微震信号的时域特征得到了较为真实的保留；频谱图中频率200～500 Hz的高频分量被最大限度的压制，频谱图中的尖峰特征可以更好地表现出来，整体上充分提取出了真实微震信号的时频域信息。

综上可知，本文提出的基于CEEMD和排列熵的降噪方法能够有效压制微震信号内部的高频噪声，同时也充分保留了微震信号内部的有效信息。