变截面修正Timoshenko梁自振频率的回传射线矩阵法分析

余云燕,孔嘉乐,陈进浩,付艳艳,李 盛

(1.兰州交通大学土木工程学院,甘肃 兰州 730070;2.中铁西北科学研究院有限公司,甘肃 兰州 730000)

0 引言

变截面梁在工程中应用广泛,如箱型变截面桥梁、变截面桥墩、海上风机塔筒、变截面水塔等。其中,海上风机与水塔在进行力学分析时,通常简化为部分埋入单桩顶端带有质量块的力学模型。针对这种稳定性较差的结构形式,应着重分析其动力特性。横向自振频率是反映结构动力特性的重要物理量,而变截面梁的振动方程是复杂的高阶变系数微分方程,除个别结构能求得解析解外[1],大部分结构的直接解析求解目前还做不到,因此需寻求适当方法获得变截面梁振动方程的精确解。

针对变截面梁振动方程的求解问题,国内外学者开展了许多研究。Ece等[2]将变截面简支梁振动方程转化为空间坐标系下普通微分方程,获得了频率方程。Tong等[3]将变截面梁等效为多段等截面微梁段,获得Timoshenko阶梯梁的振动方程近似解。Abrate[4]将变截面梁运动方程转化为等截面梁的运动方程,获得变截面梁近似自振频率。张廷芳[5]对带有变截面梁组合结构自振特性的计算方法进行了研究,建议用“变梁系数”计算变截面梁的单元刚度,用逐步降阶法凝聚总刚度阵。钱波等[6]利用有限差分法研究了变截面简支梁横向振动的自振频率。冯志刚等[7]通过构造矩形变截面梁动力单元和传递函数法,采用摄动法和Laplace变换获得梁振动频率的各阶渐进解。徐腾飞等[8]采用Frobeniu方法求解变截面梁的自由振动问题,但局限于特定截面的变化形式。针对完全弹性支承,闫维明等[9]基于Bernoulli-Euler梁理论对直接模态摄动方法进行改进,建立了求解完全弹性支承变截面梁振动方程的半解析方法。

以上对变截面梁的研究大多基于Bernoulli-Euler梁理论与经典Timoshenko梁理论。经典Timoshenko梁理论以弯曲变形来表达转动惯量,忽略了剪切变形带来的影响,故适用于弯曲变形为主的细长梁。针对长度较小的深梁,陈镕等[10]认为剪切变形不可忽视,主张以弯曲变形与剪切变形共同描述转动惯量,并提出修正Timoshenko梁理论的运动方程,研究修正带来的影响。夏呈[11]论证了修正Timoshenko梁理论只存在一个频谱,解决了经典Timoshenko梁理论存在两个频谱的争议问题[12-13]。陈治江[14]采用动力刚度法研究修正Timoshenko梁在有裂纹情况下动力特性的变化。陈镕等[15]研究了集中质量对无约束修正Timoshenko梁的正碰撞所引起的瞬态冲击响应。

经典Timoshenko梁理论中存在两组截止频率、相速度和群速度,其中一组为运算过程中数学计算的产物,没有实际意义,而修正Timoshenko梁理论中仅存在一组截止频率、相速度和群速度,物理意义更加清晰。依据修正Timoshenko梁理论求得的等截面梁自振频率的结果偏小[10],给结构动力设计提出了更高要求。修正Timoshenko梁理论考虑了剪切变形引起的转动惯量,而常见的变截面结构如桥墩、水塔等都具有短粗的特点,类比建筑结构中的深梁,其剪切变形不可忽略,故求解结构自振频率时应用修正Timoshenko梁理论更加适合。为此,本文基于回传射线矩阵法,将截面半径线性变化的变截面梁(即圆台)等效为多段等截面等效梁,将修正Timoshenko梁理论应用于变截面梁自振频率的求解中;通过具体算例,与经典Timoshenko梁理论进行对比,总结分析该修正对变截面梁自振频率的影响。

1 变截面修正Timoshenko梁回传射线矩阵法的基本原理

变截面梁(即圆台)如图1(a)所示,其长度为L,横截面半径随轴向坐标线性变化。假设材料均质、小变形,基于分段思想,将该变截面梁(即圆台)均匀分为n段,各分段长度均为l=L/n,且分段数足够多。每一分段选用所截取圆台的中位线所在截面作为该段的等效截面,如图1(b)所示。对分段等截面等效梁进行节点编号,以英文字母或数字表示节点,以两个字母或两个数字表示连接两个节点的分段梁编号,将与分段梁有关的物理量放在上标,对该等效梁建立总体坐标系(XOY)。对每一分段梁j(j+1),引入两组笛卡尔局部坐标系:(x,y)j(j+1)和(x,y)(j+1)j;坐标轴正方向如图1(c)所示,其原点分别在j点和j+1点,位移与剪力的正方向与局部坐标系的正方向相同,转角和弯矩正方向符合右手螺旋法则。两组局部坐标系的关系为xj(j+1)=l-x(j+1)j,yj(j+1)=-y(j+1)j。总体坐标系和局部坐标系均为右手坐标系。经过分段处理后,每一段等效梁较粗,应按深梁考虑,且考虑剪切变形对转动惯量的影响。

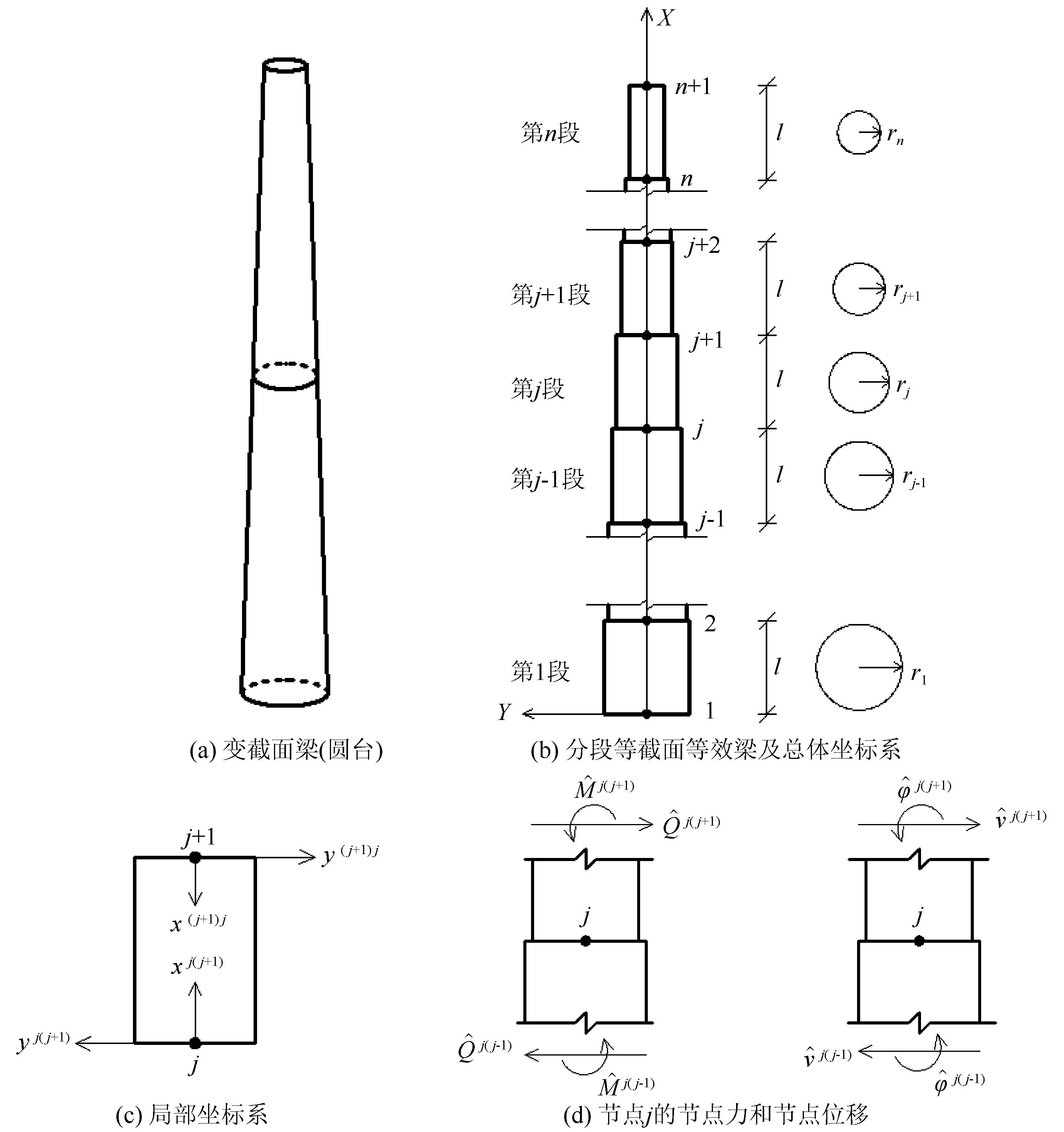
图1 变截面梁Fig.1 Variable cross-section beam

基于修正Timoshenko梁理论,在局部坐标系下,第j段等效梁的横向振动方程为:

(1)

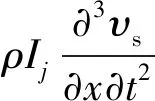
剪力、弯矩和转角可以表示为:

(2)

引入Fourier变换对,对式(1)进行Fourier变换并求解得:

a2(ω)eik2jx+d2(ω)e-ik2jx

(3)

g2j(ω)a2(ω)eik2jx+g2j(ω)d2(ω)e-ik2jx

(4)

式中:“^”表示频域中的变量;ω为自振圆频率;a1(ω)、a2(ω)表示待定入射波波幅;d1(ω)、d2(ω)表示待定出射波波幅;g1j、g2j为剪切变形与弯曲变形的比值;k1j、k2j为波数,由下式计算得到:

(5)

对应于波数k1j,2j,υs与υb的比值g1j,2j为:

(6)

总挠度υ为

[1+g2j(ω)][a2(ω)eik2jx+d2(ω)e-ik2jx]

(7)

剪力、弯矩和转角在频域中的表达式为:

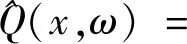
k2jg2j[a2(ω)eik2jx-d2(ω)e-ik2jx]}

(8)

(9)

ik2j[a2(ω)eik2jx-d2(ω)e-ik2jx]

(10)

在频域中对所有节点建立力平衡和位移协调条件,以边节点和中间节点j为例[图1(d)],有:

边节点1

(11-1)

边节点n+1

(11-2)

中间节点j

(11-3)

将式(7)～(10)代入式(11),整理合并为

d1=S1a1
dj=Sjaj
dn+1=Sn+1an+1

(12)

式中:

(13-1)

(13-2)

(13-3)

式(13)中:a1、aj、an+1表示节点1、节点j和节点n+1的局部入射波波幅向量;d1、dj、dn+1表示节点1、节点j和节点n+1的局部出射波波幅向量；S1、Sj、Sn+1表示节点1、节点j和节点n+1的局部散射矩阵。

鬼子队长对灯草老爹的解释深信不疑，竖起大拇指说：“你的老头，专家的有！”回转身，一把揪住刁德恒的衣领，“刁，你的八格牙路，死啦死啦的！”

将所有节点的局部出射波波幅向量dj和局部入射波波幅向量aj组集到总体矩阵d和a中,有

d=Sa

(14)

式中:d和a表示总体出射波波幅向量和总体入射波波幅向量;S表示总体散射矩阵。

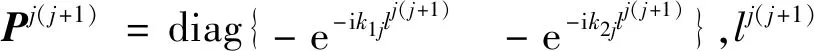
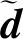
a=PUd

(15)

联立求解式(14)和式(15)得:

[I-R]d=0

(16)

式中:R=SPU为回传射线矩阵;I为单位矩阵。

要得到非零的出射波波幅矩阵d,则[I-R]的行列式必须等于零,从而得到变截面梁对应等效梁的自振频率ωN(N=1,2,…,∞)的特征方程为

det[I-R(ωn)]=0

(17)

式中：det[…]表示行列式。

(1-e-2ik1L)(1-e-2ik2L)=0

(18)

利用Euler公式将其展开,并令实部和虚部分别等于零,得到简支边界条件下修正Timoshenko梁自振时波数的解析表达式为:

(19)

式中:N*为阶数;L为等截面梁总长。

将式(19)代入式(5)中,得到简支边界条件下等截面修正Timoshenko梁自振频率ωN*的解析表达式为

(20)

其他边界条件(如两端固支、一端固支一端自由)情形下,等截面梁或变截面梁的分段数n>1时,采用黄金分割法搜索其自振频率的数值解。

2 计算方法验证

2.1 分段数对计算精度的影响

为探究分段数目n对计算精度造成的影响,设分段数n=1、2、4、8、16、32,利用回传射线矩阵法(Method of Reverberation Ray Matrix,MRRM)计算前8阶自振频率,并利用Midas有限元结果对本文结果进行验证。有限元建模中,采用100个梁单元。梁的计算参数与文献[11]完全相同(表1)。

表1 梁的计算参数[11]Table 1 Parameters for the beam[11]

在两端简支、两端固支和一端固支一端自由三种边界条件下,基于回传射线矩阵法(MRRM)求得不同分段数时的自振频率,与有限元法(Finite Element Method,FEM)计算结果进行对比,结果如表2所列。由表2可见,随着分段数的增加计算精度显著提高,当分段数为16时已具备极高精度;在算力允许的情况下,选择分段数为32可小幅度提升计算精度,但计算时长翻倍。

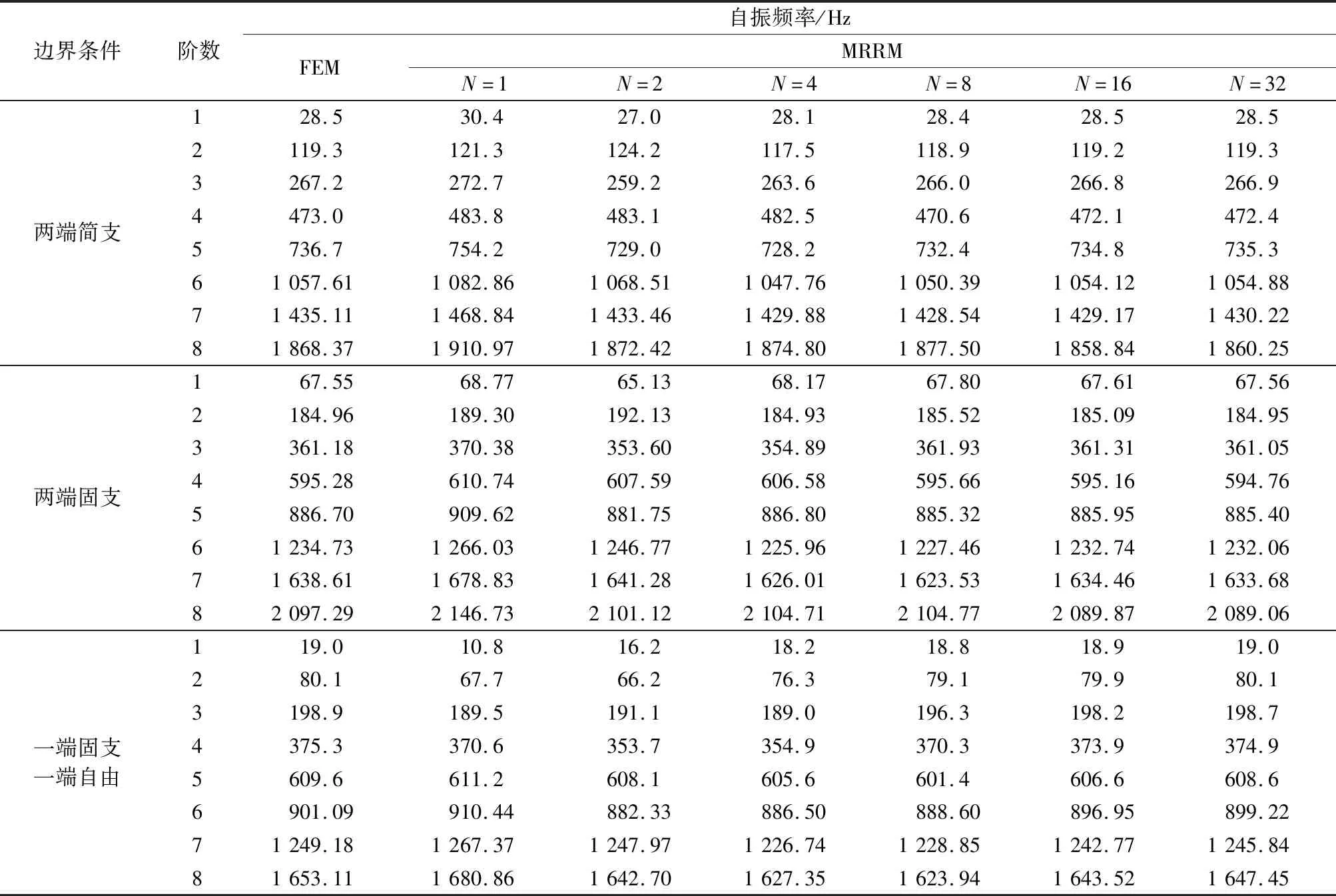
表2 MRRM 与FEM求得自振频率对比Table 2 Comparison between natural frequencies obtained by MRRM and FEM

2.2 梁长度的影响

经典Timoshenko梁理论与修正Timoshenko梁理论的区别在于横向运动方程中是否考虑了剪切变形对转动惯量的影响。在截面形式和尺寸不变的情况下,剪切变形与梁的长度密切相关,梁的长度越短,剪切变形越不可忽视,“修正”带来的影响就越大。算例分析时,梁两端截面直径保持不变(分别为0.02 m和0.01 m),改变梁长度L(分别为0.5 m、0.25 m和0.1 m),其他计算参数如表1所列。表3～5分别给出了分段数n=32时,两端简支、两端固支和一端固支一端自由三种边界条件下经典Timoshenko梁(C-T)的自振频率wCr和修正Timoshenko梁(M-T)的自振频率wMr;并以ζ值来评估修正对自振频率的影响:ζr=100×(wCr-wMr)/ωCr,ζ值越大,修正对自振频率的影响越大。

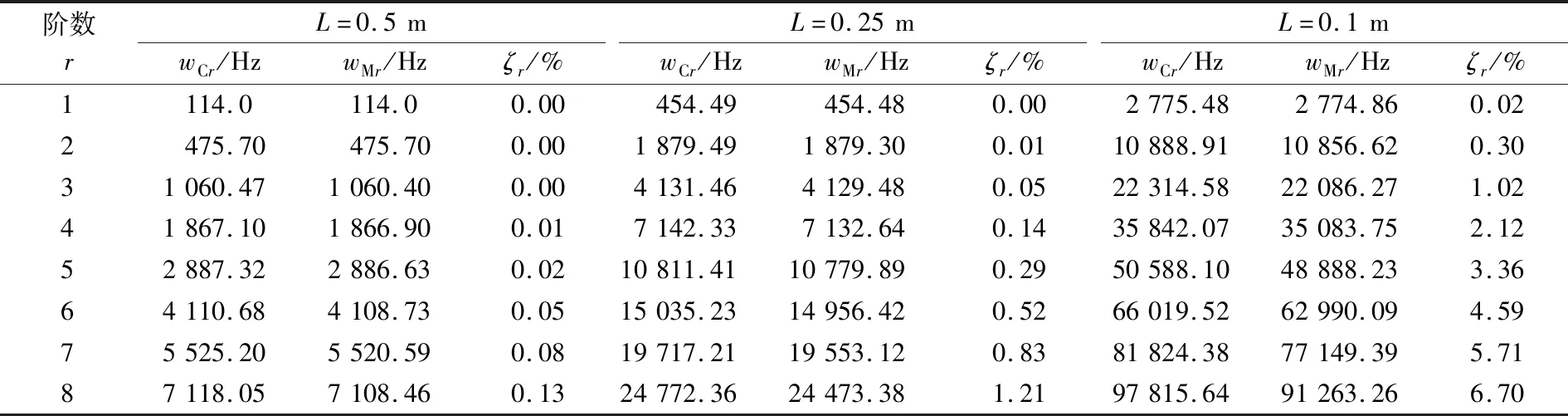
表3 两端简支边界条件下变截面经典Timoshenko梁与修正Timoshenko梁的自振频率Table 3 Natural frequencies of C-T and M-T with variable cross section under simply supported boundary condition

表4 两端固支边界条件下变截面经典Timoshenko梁与修正Timoshenko梁的自振频率Table 4 Natural frequencies of C-T and M-T with variable cross section under fixed supported boundary condition

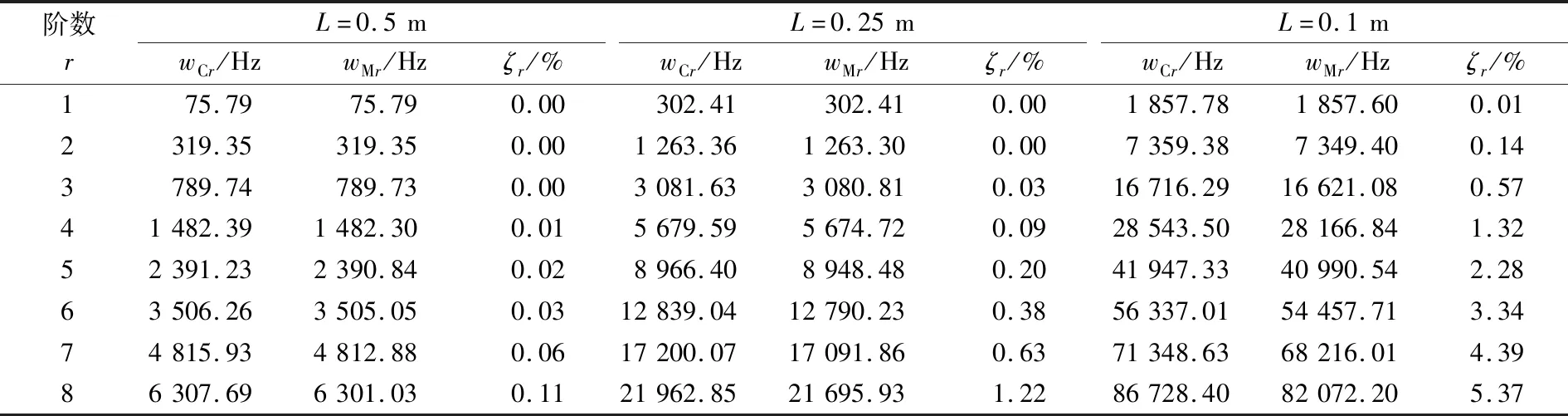
表5 一端固支一端自由变截面经典Timoshenko梁与修正Timoshenko梁的自振频率Table 5 Natural frequencies of C-T and M-T with variable cross section under one end clamped and one end free boundary condition

由表3～5可知:(1)梁的长度不变,低阶时由经典Timoshenko梁理论与修正Timoshenko梁理论得到的自振频率比较接近,随着阶数的增加,二者差值逐渐增加,且经典Timoshenko梁理论计算得到的自振频率大于修正Timoshenko梁理论的结果;(2)梁长度逐渐减小,两种梁理论得到的自振频率差值逐渐增大,阶数越高二者差值就越大;(3)梁越短粗,剪切变形对转动惯量的影响就越显著;(4)基于回传射线矩阵法,并考虑剪切变形对转动惯量的影响,将变截面梁简化为多段等截面梁的计算方法正确,具有较好的计算精度和和收敛性。

3 结论

(1) 基于修正Timoshenko梁理论,利用分段思想,采用回传射线矩阵法,通过节点力平衡和位移协调条件建立回传射线矩阵,推出截面半径线性变化的变截面修正Timoshenko梁横向自振频率的精确求解方法。数值算例表明该方法具有较好的计算精度和收敛性。

(2) 基于经典Timoshenko梁理论得到的自振频率大于修正Timoshenko梁,且随着阶数增加,两者差值增大;梁越短粗,剪切变形对转动惯量的影响就越大。

(3) 修正Timoshenko梁理论更适合于深梁。本方法还可以推广至任意变截面梁以及耦合振动计算。