叶片质量失谐下整体叶盘的振动响应特性研究*

杨铮鑫,卞天天,党鹏飞

(沈阳化工大学 机械动力工程学院,辽宁 沈阳 110142)

0 引 言

叶片—轮盘结构简称整体叶盘结构,在叶轮机械中起着关键的作用。整体叶盘具有循环对称的结构特点[1],振动模态沿圆周方向均匀一致地分布。

但是在其使用过程中,由于材料离散性、安装误差、使用磨损等各方面原因,会导致各扇区在整体叶盘间产生微小差别[2],使其结构的循环对称性遭到破坏。在结构动力学中,这种结构变异称为失谐[3]。

在整体叶盘振动过程中,失谐会导致其能量始终集中在一个或几个叶片上,即振动能量的局部化现象[4]。该现象使失谐叶片的振幅可以达到完整参考叶片振幅的数倍,从而产生局部叶片的高周疲劳(high cycle fatigue,HCF)失效[5],不仅会缩短叶轮机械的使用寿命,而且会造成重大的安全事故。

为了预测整体叶盘在失谐条件下的响应,有效避免叶片HCF风险,学者们对失谐整体叶盘的振动特性,及振动所造成的影响做了大量研究,并取得了许多重要的研究成果[1,6-8]。

近年来,许多学者对含有刚度失谐的叶片响应特性进行了深入的研究。

HUANG B H等人[9]先后采用连续性参数模型模拟的方式,在考虑科氏力效应的情况下,研究了刚度失谐对其叶盘模态局部化的影响。王红建等人[10]建立了质量—弹簧组合模型,并采用该模型,分析出了刚度失谐后,整体叶盘结构的振动响应特性。YAO Jian-yao等人[11]采用节径谱方法,对刚度失谐整体叶盘的动态特性进行了测试和模拟,通过分析得到了最优人为失谐(错频)规律,以及在刚度随机失谐情况下,整体叶盘激振力的临界现象;研究还发现,应用一定的谐波主动失谐[12]进行干涉,能够使失谐整体叶盘的稳定性进一步得到提高。

然而,以上的研究仅限于处理未发生质量失谐条件下,整体叶盘的失谐问题,而对于叶片—轮盘结构中的质量失谐问题,却并没有进行过多的描述,并且很少对整体叶盘各叶片之间(由于质量不均引发)的失谐进行研究。

若将失谐问题仅归结为简单的刚度失谐,而忽略质量失谐所带来的影响,势必会在失谐整体叶盘动力学特性的分析及模拟过程中,造成失真现象,从而在叶片疲劳损伤检测方面导致疏漏或误导[13]。

姚建尧等人[14]在航空航天研究方向的发动机失谐整体叶盘研究中,对失谐结构多种建模分析方法进行了比较,总结出了不同分析方法研究叶盘动力学方向的优缺点。LIM S H等人[15]采用质量—弹簧组合系统模拟分组拉筋结构整体叶盘模型,研究出了具有分组拉筋结构叶盘的振动响应规律[16]。ZHOU Shui-ting等人[17]采用三维有限元方法,建立了叶片拉筋结构的转子系统模型,分析出了其结构振动特性的响应规律。

在探索转子动力学方向上,国内外学者应用多种方法,进行了大量深入的研究。

一些学者采用连续参数法,建立了失谐整体叶盘模型,对失谐整体叶盘的振动响应规律进行了研究,且在研究过程中,不仅考虑了叶片的阻尼、裂纹因素,而且还考虑了复合板、带冠状等特征,使其对失谐整体叶盘响应特性的分析更加具体。

如HUANG B H等人[18]采用Eular梁与曲梁相结合的方式,对整体叶盘叶片进行模拟,分析出了整体叶盘结构特性规律。但是连续参数模型的模拟是有局限性的,板和梁在模拟过程中,因为存在人为干扰,很难真正模拟实际叶片和叶盘[19]。在某些程度上虽然能够提高模拟精度,但其模拟精度仍然较低,只适合用于机理研究[20]。

王艾伦等人[21]对失谐叶盘结构振动特性进行了研究,结果发现,叶片裂纹会使整体叶盘的振动特性产生较大的变化;通过建立了集中质量整体叶盘模型,证明了叶片裂纹扩展与失谐整体叶盘振动局部化之间存在关联。HOU F J等人[22]的研究认为,叶片裂纹会加剧整体叶盘振动的局部化程度;通过建立带有裂纹叶片的集中质量整体叶盘模型,定性研究了裂纹造成失谐的叶片对整体叶盘结构局部化的影响,并得出结论,即在非强耦合条件下,叶片基频变化不受小长度裂纹影响,而其结构耦合比和裂纹长度对叶片最大振幅有影响。

因为人为干扰因素,在研究失谐振动,分析了某些失谐叶盘结构频率转向、模态局部化、动态响应局部化及振动响应等规律时,集中参数模型会存在模拟精度低等局限性[13,23]。

连续参数法和集中参数法虽然在研究整体叶盘基本振动响应规律起到了很好的作用,但这两种分析方法同样存在局限性,在对整体叶盘方向上进行更深层次的研究时,这两种方法受到了限制。

在整体叶盘结构的进一步发展研究方面,高保真有限元模型的应用显然更加广泛。

刘铁箭等人[24]采用ANSYS,建立了发动机压气机叶片的三维有限元模型,并对其叶片进行了动力学分析,通过模拟得到了激振力下叶片的振型及谐波响应,分析了叶片工作转速下应力最大值出现的位置。Reddy等人采用涡轮-缩减编码程序,分析了受迫响应结构与气动耦合的颤振失谐,进行了气动不稳定和ANSYS结构分析,研究发现,在颤振不稳定时,空气动力效果最小[25]。

以上学者应用ANSYS三维有限元分析法,探索了转子结构动力学特性,且均取得了很好的效果。

单个叶片质量失谐方程的建立推导与裂纹叶片导致的整体叶盘失谐方程的建立推导是相似的,因此,可以采用集中质量整体叶盘模型与ANSYS有限元分析结合的方法,以此来研究单个叶片质量失谐下的系统响应变化,以便更准确地反应失谐整体叶盘的振动特性规律。

笔者基于单个叶片失谐的集中质量整体叶盘模型与ANSYS有限元分析,通过模拟叶片在质量失谐条件下的整体叶盘振动响应变化,研究单个叶片质量失谐对系统振动特性的影响规律。

1 失谐叶盘模型及运动方程

笔者建立循环对称结构的集中质量整体叶盘物理模型,如图1所示。

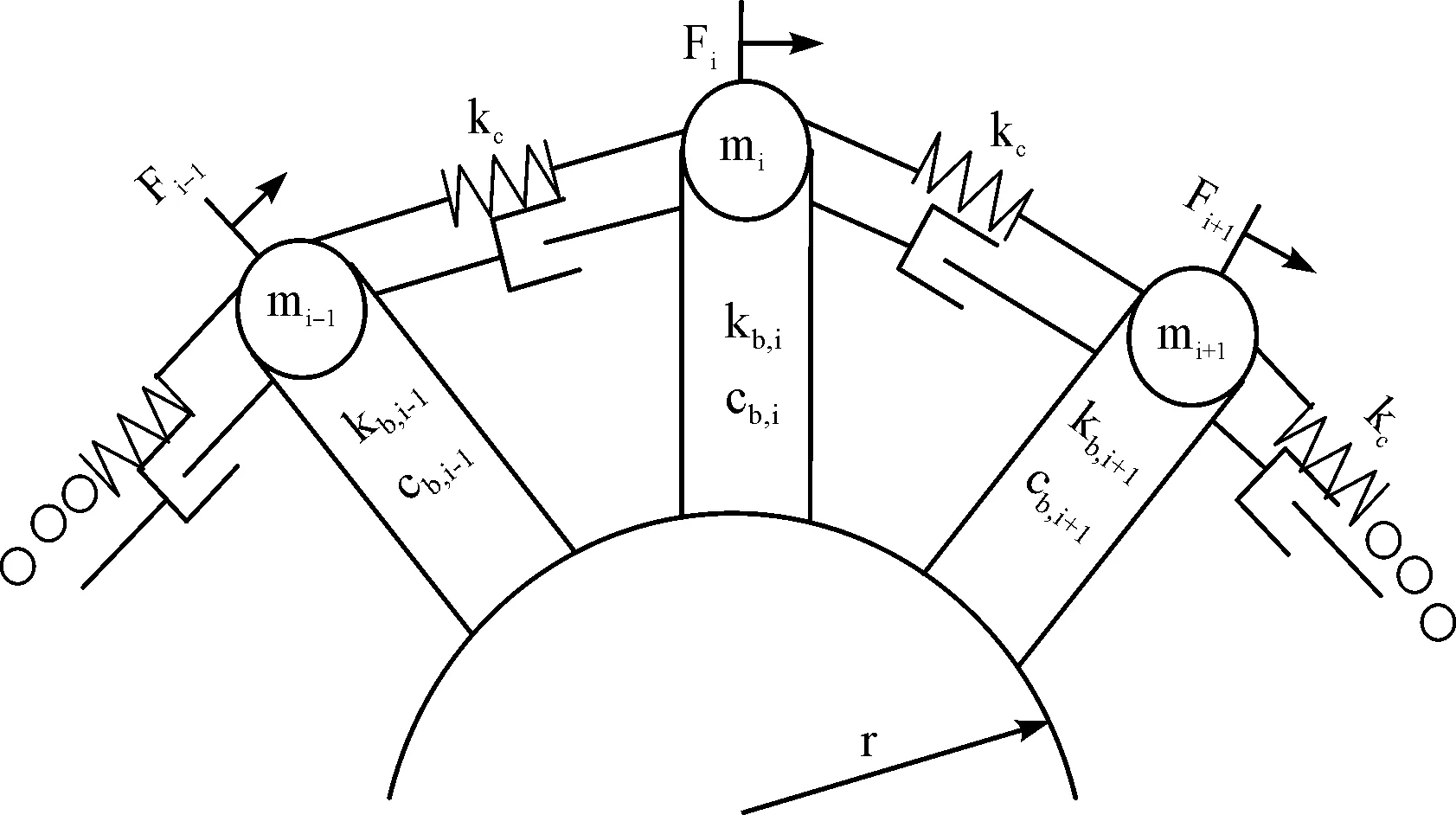
图1 集中质量整体叶盘物理模型

假设在谐调状态下,模型是半径为r的刚性轮盘,N个叶片简化为固定在轮盘上的集中质量梁,则第j个叶片固有频率为:

(1)

设叶片自身固有频率为:

(2)

在不考虑非线性因素,同时阻尼cc=0的情况下,第j个整体叶盘叶片的振动方程可表示为:

(3)

式中:xj—第j个叶片的位移;R—整体叶盘耦合强度;N—等效耦合频率;N—叶片的自振频率;Fj—谐调作用在第j个叶片上的激振力;ζ—叶片间阻尼比。

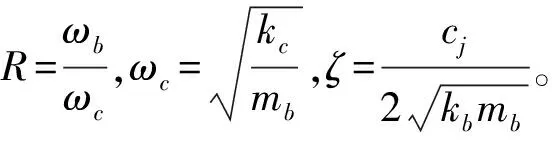
在N个叶片条件下,循环对称结构的整体叶盘振动方程可用矩阵形式表示,即:

(4)

式中:FT—激振力矩阵;M—质量矩阵;K—刚度矩阵;C—阻尼矩阵;X—位移矩阵。

整体叶盘在工作过程中,由于其旋转和非旋转部件会受到气流扰动的影响,通常将该扰动模拟为加载于谐调叶片上的激振力,因此,其扰动形式可假定为FT:

FT=Feiωt{1,eiΦ1,…eiΦj,…,eiΦN}

(5)

其中:

(6)

式中:Φj—第j个叶片上外力的相角;ω—激振力频率;E0—激振力的阶次。

其中:

XT={x1,x2…xj…xN}

(7)

(8)

(9)

在循环对称的整体叶盘中,刚度矩阵Kj通常由无损叶片广义刚度kj和耦合广义刚度kc组合而成,即Kj=kj+kc。

刚度矩阵K的表达式为:

(10)

对于循环对称的整体叶盘,所有叶片的质量,阻尼,刚度均相等,即x0≡xN,x1≡xN+1,m1≡mj≡mN。

因此,式(4)可进一步转化为以下矩阵形式:

(11)

其中,A的表达式为:

(12)

假设整体叶盘的位移为:

X=xeiωt

(13)

将式(13)代入式(11)中,可得到:

(14)

通过式(1～14),采用集中质量整体叶盘物理模型,笔者建立谐调整体叶盘的响应方程。

基于图1整体叶盘物理模型,假定N个叶片的整体叶盘中,第j个叶片发生了质量失谐,而叶片间耦合阻尼为0,并且根据质量失谐的定义,可得失谐叶片的质量为:mj=(1+ε)m。

因此,在式(4)循环结构叶片的基础上,可通过增加质量失谐量ε来简化为下式

(15)

引入质量失谐附加矩阵I0,并将I0代入式(15),可将其转化为矩阵形式的质量失谐整体叶盘结构振动方程:

(16)

其中,质量失谐附加矩阵I0可表示为:

(17)

式(16)经推导可转化为质量失谐系统的响应特性方程:

(18)

2 失谐量对整体叶盘幅频特性的影响

为了研究不同失谐强度、耦合强度、阻尼比等参数下,整体叶盘的质量失谐振动特性响应规律,基于上述的叶盘模型,笔者选定基准值叶片数N=20,耦合强度R=0.1,激振力阶次E0=2,阻尼比ζ=0.01;假设第2个叶片出现质量失谐,失谐量ε=0.1;并采用MATLAB进行模拟计算,得到质量失谐情况下,各个参数的响应特征。

取不同失谐量ε,即ε=-0.1、ε=-0.05、ε=0、ε=0.05、ε=0.1情况下,其他参数为初始值(不发生改变)时,系统的振动响应特性,如图2所示。

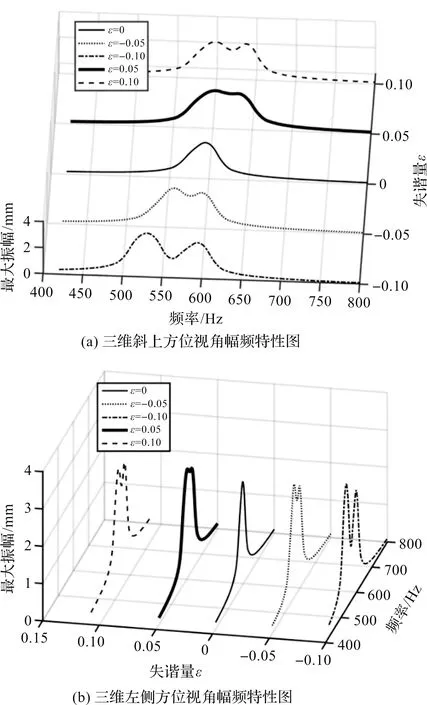
图2 不同失谐量ε的幅频特性曲线

从图2可知:与未失谐的参考叶片ε=0相比,失谐叶片在失谐量ε=-0.1情况下,失谐叶片的共振幅值由初始值2.7 mm增加到3.5 mm,并且出现多余的波峰。这说明,当叶片发生质量失谐时,整体叶盘振动的剧烈程度加剧,破坏了叶盘的稳定性;

质量失谐系统的模态与作用在整体叶盘上的激振力不具有严格的正交性,随着失谐量反向增加至ε=0.1,会出现整体叶盘的次峰值反向移动,大响应幅值的激振频率范围有所收敛,但是次峰值仍然存在,整体叶盘的振动仍然不具有稳定性。

3 不同参数整体叶盘幅频特性的影响

3.1 不同耦合强度R的影响

相比非整体叶盘模型,在质量失谐的整体叶盘条件下,整体叶盘的叶片和轮盘间的耦合关系更强。因此,对轮盘和叶片的振动响应特性进行分析时,应当将其作为一个整体结构[26]。

分别取R=0.1、R=0.2、R=0.3、R=0.4、R=0.5,而其他参数为基准值时,系统的响应幅频特性图,如图3所示。

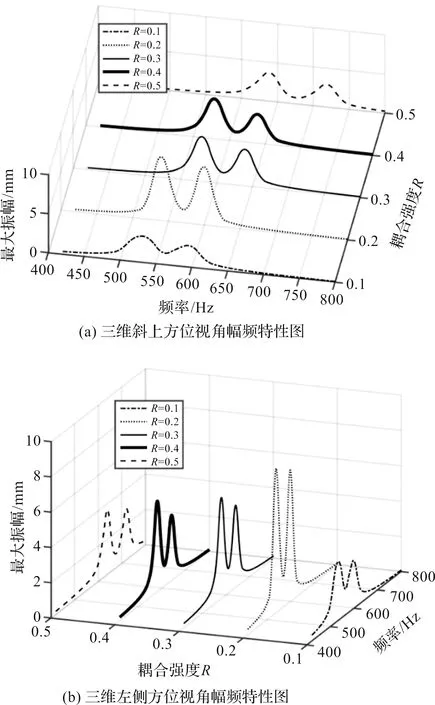
图3 不同耦合强度R下的幅频特性曲线

由图3(a)可知:耦合强度R增大,会使系统的最大响应峰值向右偏移。该现象说明：随着耦合强度R增大,整体叶盘的刚度增加,使系统的固有频率也跟着增加;

在低耦合R=0.1条件下,系统的响应激振频率变化范围更广,激振敏感区变化范围在450 Hz～650 Hz;低耦合向中高耦合R=0.4过渡时,激振敏感区缩减至500 Hz～650 Hz。这一现象说明,在低耦合条件下,失谐整体叶盘对失谐条件更加敏感。

由图3(b)可知:当耦合强度R从0.1增加到0.2时,系统的响应峰值出现增加趋势;而当耦合强度R从0.2增加到0.5的过程中,系统的响应峰值出现了降低。该现象说明,在低耦合条件下,增大失谐系统耦合数会使系统响应幅值增大;而在高耦合条件下,增大耦合强度会降低系统的响应峰值,从而起到了一定的积极作用。

以上现象表明,仅依靠单方面增加耦合强度,不能有效地控制系统的响应幅值。

3.2 不同阻尼比ζ的影响

当失谐整体叶盘的阻尼发生改变,即ζ=0.001、ζ=0.004、ζ=0.006、ζ=0.008、ζ=0.01时(其余基准值不变),质量失谐整体叶盘的幅频特性曲线,如图4所示。

图4 不同阻尼比ζ的幅频特性曲线

图4中,当阻尼比增大时,质量失谐整体叶盘的振动幅值会相应地降低。阻尼系统是工程师为有效地降低叶盘的振动,提高叶盘疲劳寿命而设计的一种结构,它对于减小叶盘(由于失谐引起)振动可以起到促进作用[27]。

在单个叶片质量失谐的整体叶盘同样是适用的,阻尼比的增加使得系统除主峰值外的其余峰值变化趋于平缓,各波峰间的峰值差减小,即波峰钝化现象。该现象表明,系统阻尼的增大仍对改善失谐整体叶盘的振动响应具有促进作用。

4 ANSYS仿真模拟及验证

由于使用三维有限元分析法能够更精确地描述失谐整体叶盘的振动特性,笔者采用ANSYS建立三维失谐整体叶盘结构模型,如图5所示。

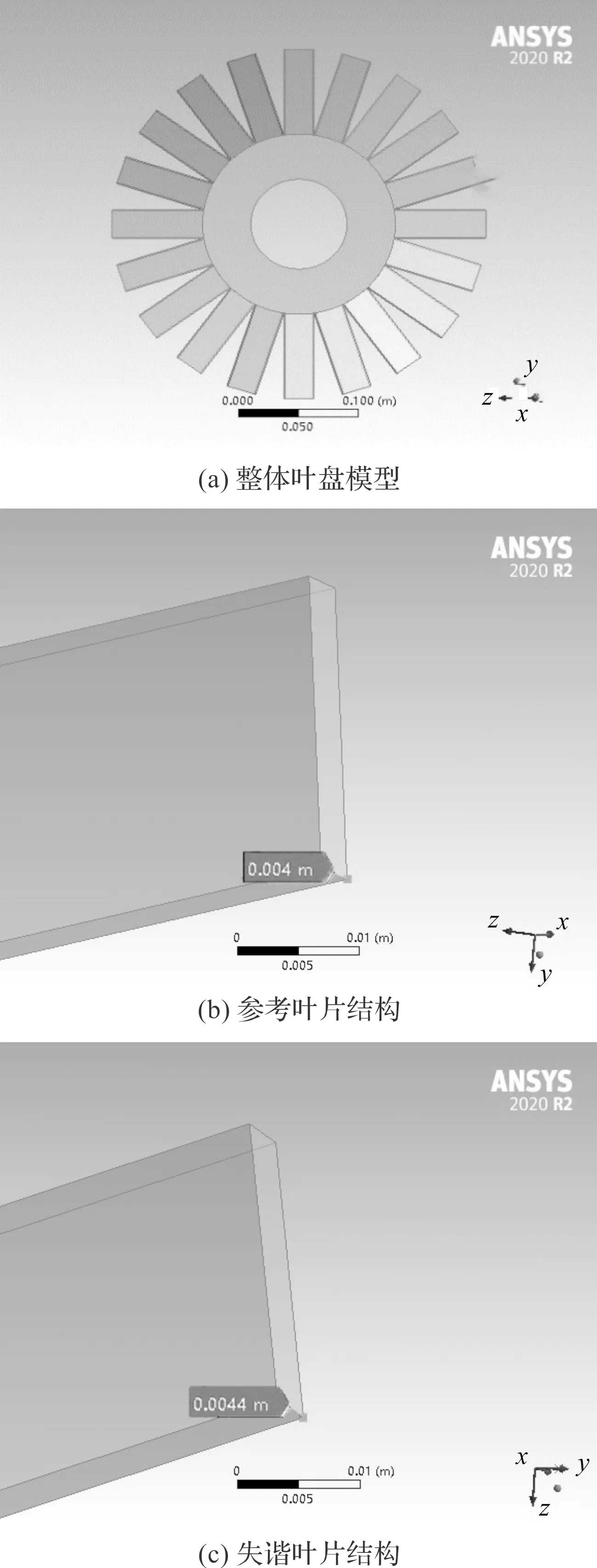
图5 失谐叶盘有限元模型

笔者通过改变叶片几何结构的方式,削减叶片厚度,使用ANSYS模拟叶片质量失谐,对整体叶盘进行谐响应分析,得到失谐叶片及不同参数在叶片质量失谐下的响应特性曲线。

其中,不同失谐量ε下的幅频特性曲线如图6所示。

图6 不同失谐量ε下的幅频特性曲线

不同耦合强度R下的幅频特性曲线如图7所示。

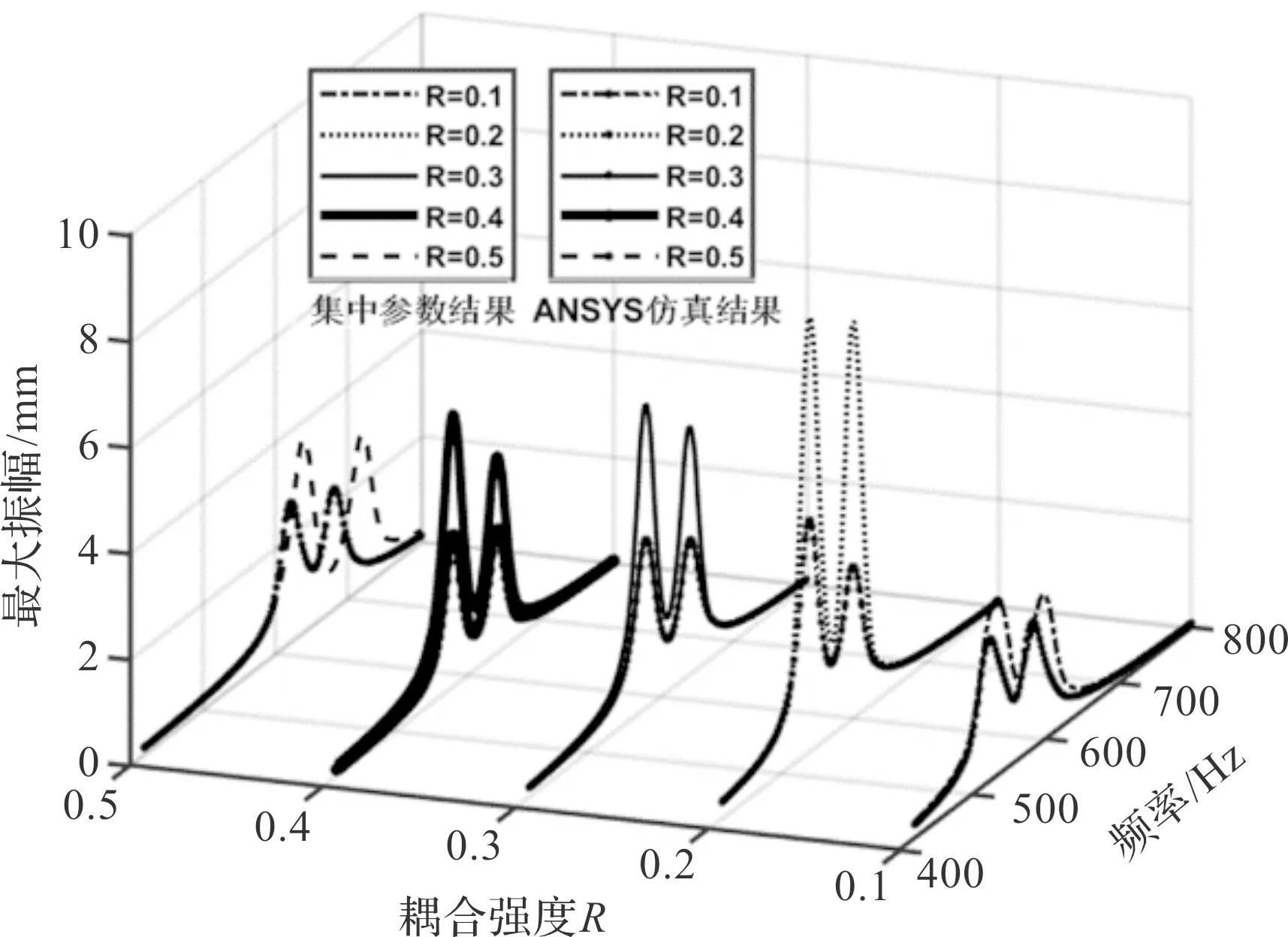
图7 不同耦合强度R下的幅频特性曲线

不同阻尼比ζ下的幅频特性曲线如图8所示。

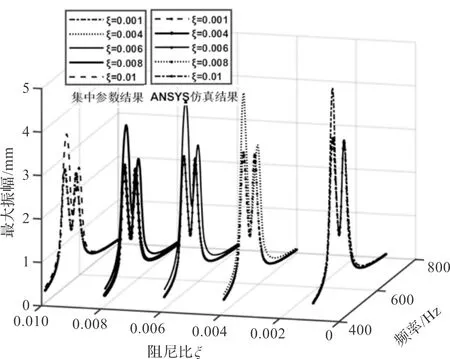
图8 不同阻尼比ζ下的幅频特性曲线

由图(6～8)可知:

在研究叶片质量失谐对整体叶盘的振动响应时,采用集中质量法与有限元分析法,所得结果仍然会存在小范围的误差,但两种方法所得到的响应特性规律基本吻合,不影响最后的判断结果。

5 结束语

叶轮机械的整体叶盘中,由于叶片质量的分布不均,会产生叶片质量失谐、振动局部化等问题,为此,笔者对失谐整体叶盘的振动响应特性规律进行了研究。首先,建立了整体叶盘物理模型,绘制出了不同叶盘参数下的幅频特性曲线;然后,建立了不同叶片厚度的整体叶盘三维有限元模型,对其振动响应特性进行了分析,并绘制出了幅频特性图;最后,总结出了各项参数对系统振动特性的影响规律。

研究结论如下:

(1)单个叶片质量失谐很大程度上会破坏整体叶盘结构正常工作的稳定性,使整体叶盘系统的振幅有所增加,并且出现多余峰值,在幅频特性曲线上可以很好地体现出来;

(2)耦合强度对于质量失谐整体叶盘的振动特性有非常重要的影响,不同耦合强度的工作环境,其响应幅值变化趋势也不同。在低耦合强度下,质量失谐对系统的响应更加敏感;在某些情况下,改变耦合强度会对系统产生一定的积极效果;使系统振幅减小,响应频率变化范围也会根据耦合强度的大小进行调整;

(3)改善阻尼对优化失谐整体叶盘的幅频特性具有促进作用,增大整体叶盘的阻尼比能够有效地减小系统的响应振幅。在设计和制造叶盘的过程中,可以通过控制整体叶盘耦合强度和阻尼比,使系统远离共振区域,延长叶轮机械的使用寿命。

在叶片质量失谐整体叶盘的实际工作环境中,需要充分地考虑各种叶盘参数条件下的失谐系统振动响应特性。因此,在后续的工作中,笔者将对此进行更进一步的探索。