基于分离涡模拟的旋转射流流场结构特征分析

陈健翔，杨睿月，黄中伟，李根生，秦小舟，李敬彬，武晓光

（1. 油气资源与探测国家重点实验室，北京 102249；2. 中国石油大学（北京），北京 102249）

0 引言

高压水射流技术作为一种高效的破岩方法，广泛应用于石油钻井、煤矿开采、巷道掘进等领域[1-2]，但由于破岩门限压力高、现场泵压受限等情况，很难达到体积破碎的效果，导致破岩比能较大[3]。旋转射流通过在喷嘴内部增加叶轮导向元件，使得射流质点形成三维速度，在垂直冲击岩石产生拉伸[4]、水楔作用的同时，还增加了平行于岩石表面的切向载荷[5]。前人实验表明对于同种岩石，旋转射流的破岩门限压力仅为普通直射流的 60%左右[6]，因此可显著提高射流的破岩效率[7]。此外，旋转射流的扩散特性使其破岩面积达到普通直射流的10倍左右[8]，同时产生的冲击回流呈旋转状向外辐射，减少了直射流中冲蚀孔内回流对射流柱的干扰，亦有助于破岩效率的提高。

旋转射流具有高效破岩能力的根本原因是其特殊的旋流流场结构，因此许多学者针对旋转射流的流场分布进行了大量研究。步玉环等[9]和Ni等[10]利用五孔探针测量了旋转射流在淹没状态下的速度分布，发现轴向速度剖面呈“M”形分布，切向速度剖面呈“N”形分布。王耀锋[11]研究发现在淹没条件下，旋转射流径向速度分布大致呈“M”状，旋转射流产生的切向速度使射流扩散角增大，但淹没条件下切向速度的轴对称分布特征较弱。李向东[12]基于流体旋转流动和多相流动力学理论，采用计算流体动力学软件FLUENT对旋转磨料射流流场进行了数值模拟，对比分析了不同结构参数对喷嘴工作性能的影响。吴德松等[13]通过数值模拟分析了叶轮旋槽出口角度、叶轮面积、混合腔收敛角等喷嘴结构参数对射流流动的影响规律。前人的研究主要关注流场速度分布以及喷嘴结构对流场的影响规律，忽略了大量的流场细节特征且少有文献研究旋转射流流场的发展过程，如射流剪切层中湍流脉动的发展特征以及大涡结构的演化过程等。为了了解旋转射流的流动特性从而选择合适的工程应用场景，本文拟采用数值模拟的方法对旋转射流流场演化进行深入研究。

当前研究射流流场常用的数值模拟方法包括雷诺时均法（RANS）和大涡模拟法（LES）。RANS法基于雷诺平均方程对流场的时均特性进行研究，具有计算量小的优势，但只能预测湍流的平均速度场、平均标量场和平均作用力[14]，无法精细捕捉流场中不同尺度的涡结构变化。LES法通过精确求某个设定尺度以上所有的湍流运动，从而有效地处理自由射流、剪切湍流等非稳态复杂流动[15]，但由于其对壁面边界层的分辨率要求较高，网格数量巨大，受到计算资源的制约[16]。分离涡模拟（DES）方法，也称耦合的 LES/RANS算法，兼有大涡模拟精度高和雷诺时均湍流模型计算量小的优点，对高雷诺数湍流问题具有更好的适用性。DES法通过对边界层内的流场采用RANS湍流模型解析，对边界层以外大涡主导的湍流区借助LES计算，同时保证了近壁区的计算速度和远离壁面区域流场的解析精度[17]。目前，已有多种RANS湍流模型应用于DES法，包括Spalart-Allmaras模型、可实现k-ε模型、剪应力输运模型（SSTk-ω）和过渡SST模型[18]。

本文采用基于DES改进的IDDES方法（Improved Delayed Detached Eddy Simulation）配合SSTk-ω湍流模型对高雷诺数下的旋转射流流场进行模拟，研究了旋转射流涡量场、速度场、压力场的演化过程，探索了喷嘴压降对大涡结构发展和湍流脉动波动的影响规律，揭示了旋转射流的产生机理和流场结构特征，为旋转射流选择合适的工程应用场景提供理论指导。

1 数值模拟模型

1.1 数学模型

模型的建立基于以下假设：①忽略温度变化对流体的影响；②不考虑射流撞击过程中的能量损失；③固体壁面为无滑移的光滑表面。

1.1.1 控制方程

本文中的高压射流冲击过程属于非定常黏性流动，计算流场时首先需要满足连续性方程和动量方程，其控制方程如下：

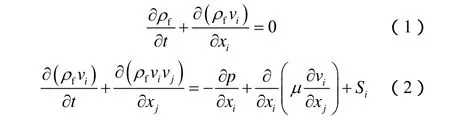
1.1.2 湍流模型

本文研究对象为高雷诺数下的射流冲击流场，采用基于DES改进的IDDES方法配合SSTk-ω湍流模型进行计算。改进后的模型在边界层计算时可实现LES解析对数层和RANS模拟对数层之间的调整，解决对数层不匹配的现象，IDDES为高雷诺数流场提供了更灵活的尺度分辨仿真方法[19]。SSTk-ω湍流模型是一种两方程涡黏性湍流模型，该模型考虑了湍流剪切应力的运输，既可以应用于低雷诺数条件下的湍流模拟，没有额外的黏性衰减函数，又可应用于远离壁面边界层以外的区域[20]。因此，SSTk-ω模型相较于其他模型在逆压力梯度流动、翼型跨音速激波等流动场景下，具有更高的精确度和更广泛的适应性。一般条件下SSTk-ω湍流模型中，湍动能k和比耗散率ω的输运方程分别为[21-22]：

1.2 几何模型与网格划分

根据旋转射流喷嘴几何结构，提取流道得到旋转冲击射流流场模型（见图1a），设置坐标原点为叶轮顶部中心。流场模型主要包括内置叶轮的旋转喷嘴流场和外流场两部分，其中叶轮内流场由3个呈旋转对称的螺旋流道组成，旋转角为360°。喷嘴直径D为5 mm，外流场区域设定为长70 mm、宽70 mm、高80 mm的长方体。射流过程中高压流体从喷嘴入口流入，经叶轮导向旋转以及收缩段、发展段加速后，呈螺旋放射状进入外流场，冲击至底部平面后产生漫流，并沿径向方向流出外流场。模型采用压力入口与压力出口边界条件，旋转喷嘴壁面及底部冲击面采用标准无滑移壁面边界条件。

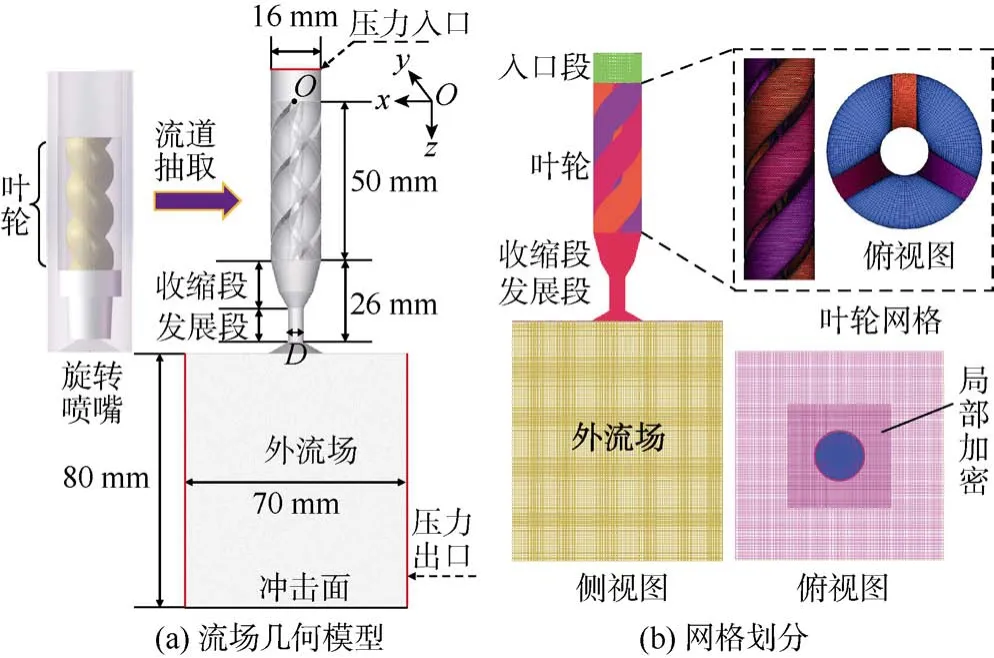
图1 旋转射流流场数值模型

将建立的旋转射流几何模型导入前处理软件ICEM CFD（The Integrated Computer Engineering and Manufacturing Code for Computational Fluid Dynamics），为提升网格质量，增强计算精度和收敛性，采用结构化网格划分（见图1b）。针对旋转喷嘴复杂的流道结构，网格构建时将整体模型划分为 4个子块（入口段、收缩发展段、叶轮段、外流场），分别建立拓扑结构，各子块网格之间采用界面连接：入口段和收缩发展段为类圆柱型，采用O型网格划分技术，提升网格在圆形边界处的质量；叶轮段由多组弯曲流线构成，采用分段切割、旋转对称的方式对模型进行网格离散；外流场为矩形，是旋转射流的主要演化发展段，为提高计算效率同时精确捕捉旋转射流复杂的湍流特性，对射流剪切层内的区域进行网格局部加密。由于外流场为大涡主导的湍流区，主要借助 LES计算湍流分布，LES的截止尺度主要和当地网格尺度相关，可根据需求的涡系结构大小选择网格尺寸[24]。综合考虑计算效率和流场分辨率的影响，最终选定外流场网格大小为0.6 mm，中心加密网格大小为0.3 mm；此外，考虑边界层影响，对旋转喷嘴壁面网格进行了加密处理，加密完成后整体流场网格数量为730×104，网格质量保持在 0.6以上，可满足高速流场的模拟需要[25]。为进一步提高DES模拟的准确性，模型的推进求解速度应大于实际物理扰动传播的速度，从而获取射流过程中小尺度的涡旋结构。本文模拟时间步长Δt设为1×10-6s，对应库朗数小于0.6，可达到较好的模拟精度[16]。模型中的射流流体为液态水，其黏度为1.003×10-3Pa·s，密度为 998.2 kg/m3，模型入口压力和出口压力（出口压力即环境围压）分别为30，20 MPa，单位时间迭代步数为40。

1.3 数值模型验证

为验证数值模型的准确性，采用Tummers等[26]的实验数据作为验证标准，该实验研究了雷诺数为23 000时充分发展的紊流的冲击射流场，并对冲击流场的速度分布特征进行了精细测量，被学者广泛认可，具有较高的可信度[27-28]。Tummers等的实验采用圆管冲击射流，与本文冲击射流流场具有一定相似性。本文采用基于SSTk-ω模型的IDDES方法，对实验条件下的冲击流场进行了模拟，以验证在冲击射流流场条件下湍流模型计算的准确性。图2a和图2b分别为射流中心轴线以及距喷嘴出口7 mm截面处的速度分布，图中采用无量纲速度项v/va表征速度大小，v为流场中相应位置的流体速度，va为喷嘴出口处的平均速度。数值计算结果与实验数据吻合较好，验证了本文采用的湍流模型计算冲击射流流场的准确性。

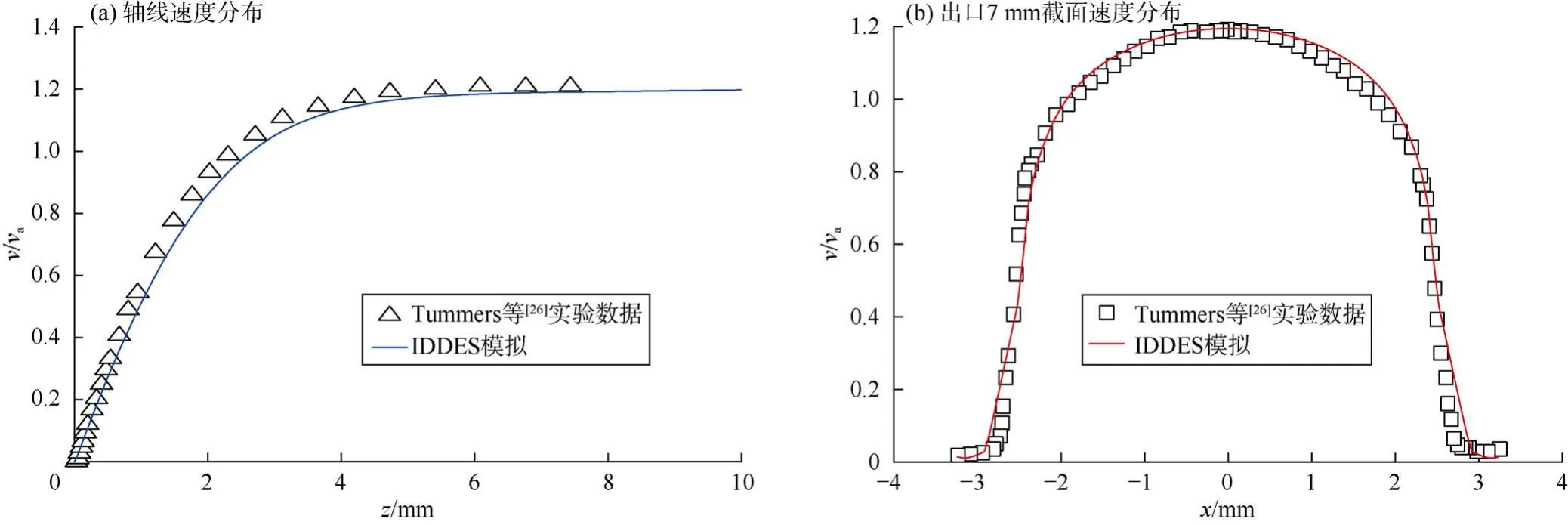
图2 模拟结果与实验数据的对比

2 模拟结果分析

2.1 涡量分布特征

2.1.1 旋转射流涡演化过程

旋转射流涡结构时序演化过程如图3所示，可通过三维涡旋单元的变形、拉伸和破碎过程来描述湍流在表面无序的运动中的变化情况[15]。本文使用Q-准则等值面[29]对涡的拟序结构进行识别和表征，采用轴向速度对涡结构进行着色。根据涡旋发展形态并结合前人对旋流的研究基础[30]，本文将旋转射流涡旋的演化划分为3个阶段：Kelvin- Helmholtz（K-H）不稳定性阶段、过渡阶段和旋转不稳定性阶段。

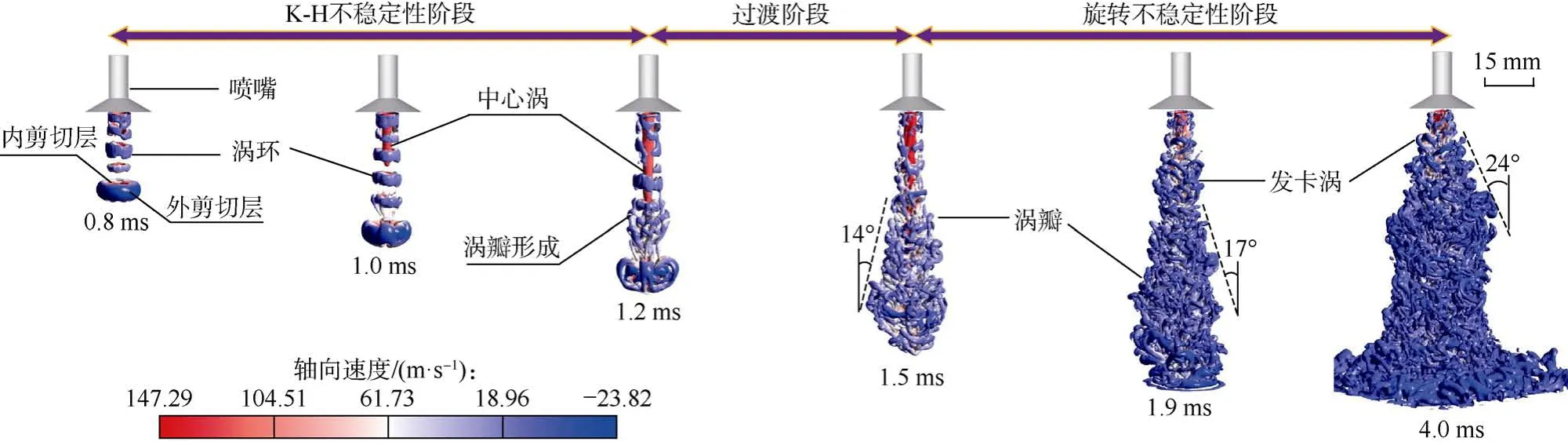
图3 旋转射流涡旋结构演化历程

旋转射流初入外流场时，主要受剪切层内的 K-H不稳定性控制，流体发生内螺旋汇聚，形成垂直于射流方向的涡环序列，尺寸与喷嘴出口相近。涡环由内、外剪切层两部分组成，内剪切层速度较高、与射流方向一致，外剪切层速度较低、与射流方向相反，在这一阶段涡旋结构整体处于相对稳定的发展期。

随着射流的推进，旋转不稳定性增强，促使射流剪切层失稳，涡环的周向拟序性下降，出现拉伸断裂，在涡环边缘开始发生涡卷起与涡配对现象并形成涡瓣结构。同时，中心涡结构在涡环内部产生并沿轴线向下延伸，前人在旋流燃烧器的流场中也观察到了这一结构的存在[30]。在1.2 ms左右出现“涡旋破碎”现象[31]，即射流端部发生回流，通常认为回流区的产生与旋转效应引起的离心力有关[32]。依据连续性方程和伯努利方程，由于周向速度的存在，射流轴线附近将产生径向压力梯度。在射流出口附近周向速度高，旋转效应强，使得射流轴线处压力显著降低；而在射流的下游，周向速度衰减，旋转效应减弱，轴线附近压力逐渐恢复。因此射流轴线附近形成了上游压力低、下游压力高的“逆压梯度”现象[31]，当逆压梯度达到一定程度时流体发生回流，进一步促进了射流与环境流体（外部流场中的流体）的混合，增大了射流扩散范围。1.9 ms时射流冲击至底部平面，射流形态进一步发展，涡瓣破碎程度增加，在冲击面出现径向漫流。

随着射流的持续推进，在4.0 ms左右射流形态已充分发展，射流的旋转不稳定性占据主导位置。周向速度的发展增加了内外流体的动量交换，射流沿径向进一步扩展，在剪切层附近形成了典型的发卡涡和流向涡结构[31]。同时，射流下游的大尺度涡结构发生相互作用与合并，不断破裂形成新的小尺度涡结构。在充分发展的旋转射流阶段，旋转效应导致的径向扩展有利于增大射流扩散角，提升射流冲击面积。

流场稳定后，在外流场涡旋分布云图中以流线疏密程度表征涡结构的变化，以速度矢量表征流体的运动方向（见图4）。由图可知，流线分别由喷嘴内部流出和周围环境流体卷入。其中来自喷嘴内部的流体大多沿射流轴线直接冲击至底部平面后沿径向方向离开流场，而由外部流场卷吸进入的流体是剪切层中涡旋的主要来源。通过剪切层中涡结构的分布可知，小涡旋在喷嘴出口附近形成，而后随着射流的推进，涡旋逐渐发育扩展。在2.9 ms时流场中主要存在3个大的涡旋结构A、B和C，其中涡旋A又逐渐分化为A′和A″。由流线的疏密变化可以发现，涡旋强度变化整体表现为先减小后增大。首先，随着射流的推进，剪切层中的大尺度涡结构将射流外围的低速流体卷入射流内部，涡旋强度逐渐降低，表现为流线密度下降。但当流体接近冲击面底部时受径向漫流和驻点处流体聚积影响，流线密度增加，流场的涡旋强度再次增大。

图4 外流场涡旋分布云图

2.1.2 压降对涡结构分布的影响

由不同压降条件下外流场涡结构的分布云图可知（见图5a），涡旋的分布位置在演化过程中总体保持一致，表明增大射流压降并不会对涡结构的分布产生显著影响，但射流的扩散范围及喷嘴出口附近的剪切层中发育的小涡结构数量略有增加。这是由于随着射流压降的增加，射流速度大幅增大，依据伯努利原理，静压力将显著降低，进一步增大了剪切层内流体与环境流体的压差，增强了卷吸低速流体进入射流内部的能力。

图5 不同压降下外流场涡旋结构分布云图（a）和螺旋度分布云图（b）

图5b为外流场螺旋度分布云图，螺旋度为速度矢量和涡度矢量的点积，表征流体沿旋转方向运动的强度，其正负值反映了射流速度对涡旋的输运方向，在气象领域常用于表征气流对龙卷的输运强度[33]。本模型中随着压降的增大，射流螺旋度增加，其最大螺旋度由 3.09×107m/s2增至 6.06×107m/s2，增长 96.12%；流体旋转强度增大的同时，流场对旋流的输运能力增强，核心区长度由 1.5D（1.5倍喷嘴直径）增长至 3.4D，增长128.57%。虽然核心区长度显著增加，但喷嘴出口附近流场对旋流输送能力的增强并没有明显改变下游涡旋的分布，这是由于旋转射流涡旋的强烈耗散作用使得螺旋强度在射流下游快速衰减。

2.2 速度分布特征

2.2.1 流场演化与速度分布

由旋转射流速度分布云图可知（见图6a），当射流初入流场时，射流整体结构还未充分发育，射流形态呈纺锤型。2.0 ms左右射流冲击到底部平面，产生径向漫流，同时在射流剪切层的卷吸作用下射流扩散角逐渐增大，旋转射流形态初步形成。随着流场的演化，射流不断从环境卷吸低速流体，在3.0～4.0 ms时流场形态已充分发展，射流核心速度及扩散角稳定，而在射流核心区外部，射流流体与环境流体充分扰动，同时伴随着总压和速度的下降以及湍流脉动的增强。由射流轴线上的速度分布可知（见图6b），相较于4.0 ms的稳定流场，1.5 ms的发展中流场在喷嘴出口附近的速度更高，波动幅度更小。这是由于在此阶段射流旋转形态还未形成，湍流脉动较弱，因此速度衰减更缓慢，同时进一步证实了旋转射流速度衰减的主要原因是旋流效应引起的湍流脉动耗散。

图6 旋转射流速度分布云图（a）及轴向速度分布（b）

压降为10 MPa、射流时间为4.0 ms时旋转射流不同速度分量的分布云图及相应无因次喷距（即喷嘴出口到冲击面的轴线距离与喷嘴直径的比值，以下简称喷距）下的分布曲线如图7所示。将旋转射流的速度分解为 3个方向（x、y、z），其中射流的旋转效果由vx和vy决定，而对旋流的输送能力由vz决定。径向速度分量vx和vy整体呈旋转对称分布（见图7a），在喷嘴出口附近为对称形式较规则的“N”形（见图7b）；随着喷距的增加，周围低速流体被卷吸进入剪切层，射流范围逐渐增加，对称形式减弱，速度迅速衰减。速度分量vz在喷嘴出口附近分布呈“M”形，速度较高，同样随着喷距的增大，“M”形分布逐渐消失，速度快速衰减，与前人实验观测结果一致[9]。旋转射流相较于直射流，虽然减小了射流等速核的长度且耗散较快，但是较高的周向速度增大了射流的径向扩展速率和湍流脉动强度。在喷嘴出口附近，旋转效应能够显著增强湍流脉动，尤其是径向湍流脉动，使得速度曲线呈现明显的对称形式；而在射流下游，湍流耗散效应引起湍流脉动的迅速衰减，射流对称形式减弱，速度快速降低。

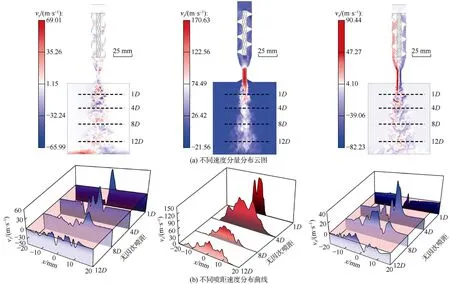
图7 不同速度分量分布云图（a）及不同喷距下速度分布曲线（b）

图8为压降10 MPa、射流时间4.0 ms时旋转射流周向速度分布云图，周向速度的大小反应了旋流能力的强弱，首先截取喷嘴内部关键节点的周向速度分布（见图8b）。刚进入叶轮段时（AA′），流体沿叶轮流道进行顺时针方向（正值）的螺旋运动，由于受离心力影响，流道外侧流线密度较内壁更大，同时流体内部发育小的逆向涡旋。经过叶轮的旋转导向，到达BB′时喷嘴内流线分布均匀，流体内部逆向涡旋结构达到稳定，逆向速度显著降低。随着射流的推进，当流体进入收缩发展段时（CC′），由于截面收缩，流体向中心汇集，最大周向速度增加，中心的涡旋强度开始增大。当流体到达收缩发展段出口时（DD′），经过加速的流体最大周向速度较截面AA′提高了197.87%，涡旋强度达到最高。从外流场周向速度分布云图看出（见图8c），在喷嘴出口附近，周向速度保持较好的旋转特征，围绕射流中心形成涡旋结构。但随着喷距的增大，周向速度被不断耗散，中心涡结构的强度逐渐降低。此外，射流与环境流体掺混，在射流剪切层边缘形成新的涡结构，进一步增大了湍流耗散的强度。喷距达12D时，射流的最大周向速度较喷嘴出口处降低了67.49%，且没有形成明显的核心涡旋，旋流强度已被大幅削弱。

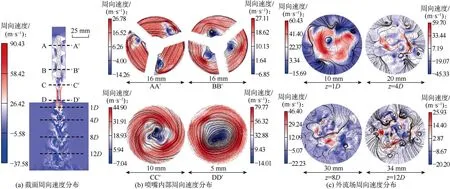
图8 旋转射流周向速度分布云图

通过分析周向速度的变化，发现旋转射流周向速度的形成主要来源于叶轮的旋转导向作用，而旋流强度的增加则取决于收缩发展段的结构特征。因此在喷嘴结构设计中适当增加收缩发展段的长度将有利于形成更高的周向速度和轴向速度，在增加旋流强度的同时增大对旋流的输送能力，从而增大外流场中旋流的推进距离，削弱湍流耗散的影响。

2.2.2 压降对旋转射流速度分布的影响

由不同压降下的外流场速度分布云图可知（见图9a），随着射流压降的增加，整体射流形态并没有明显变化，但更高的压降使得射流对周围流体的卷吸能力增强，射流扩散角逐渐增大，旋转射流的冲击范围也相应增加。射流中心轴线上的速度分布曲线如图9b所示，随着压降的增加，射流速度和脉动幅度都相应增大，但喷距达约0.125 m（z=9D）之后，不同压降条件下的速度大小基本保持一致。不同压降下的速度分布曲线的整体波动具有相似性，在压降为25，20，15，10 MPa的条件下从喷嘴处到z=9D附近的降幅分别为71%，68%，62%，53%，受到旋转射流湍流脉动的影响，高压条件下的速度衰减梯度更大。

图9 不同压降下旋转射流速度分布云图及轴线速度分布曲线

由不同速度分量分布曲线可知（见图10），由于压降增大了旋流强度，使得喷嘴出口附近的射流对称性增强，vx和vy呈“N”形对称分布的规律更明显；但随着喷距的增加，射流径向扩展范围逐渐增大，vx和vy快速衰减，速度对称性减弱，在z=4D处压降影响已基本耗散。相较于径向速度，压力变化对轴向速度vz的提升更为显著，压降由10 MPa增加至25 MPa时，在喷嘴出口z=1D处最大速度增加了约79.19%，且射流速度分布更集中，但当喷距达到9D～10D时，压降的影响基本耗散。

图10 旋转射流不同速度分量分布曲线

2.3 压力分布特征

2.3.1 压力分布与外流场压力演化

从压降为10 MPa、射流时间4.0 ms时的旋转射流压力分布云图看出（见图11a），流体进入喷嘴后，压力在叶轮段内基本保持稳定；到达收缩发展段后由于速度迅速增加，依据伯努利原理，压力开始降低，最低压力达到15.4 MPa，远小于环境围压20.0 MPa，在喷嘴出口附近形成“负压”状态；进入外流场后，低压区呈螺旋状向下游传递，结合流线分布特征发现，射流剪切层中的涡结构主要发育在螺旋状的低压区边缘。在磨料射流工程的应用场景中，旋转射流形成的低压区有利于促进射流与磨料颗粒的混合，相较于普通的直射流可显著提升磨料颗粒的冲击强度和冲击范围，充分发挥旋转射流的优势。

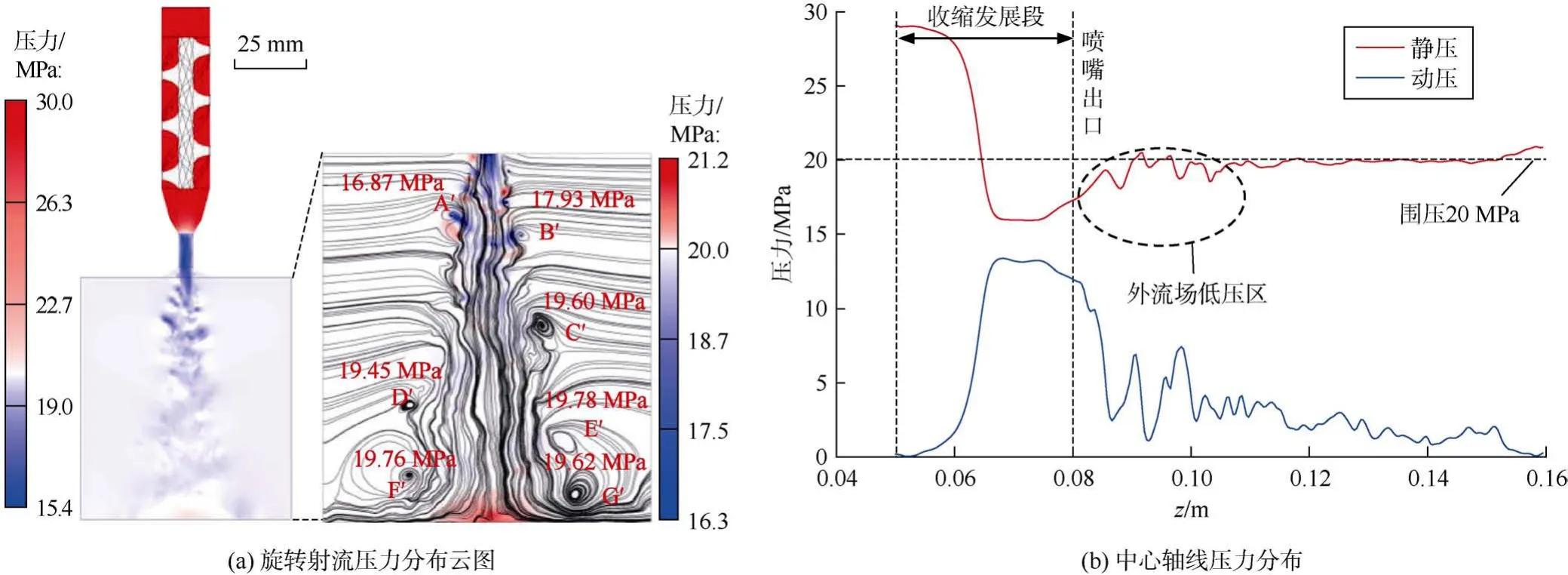
图11 旋转射流压力分布云图（a）及轴线压力分布（A′—G′表示不同涡旋，数值为对应涡旋中心的压力值）

图11b展示了动压力与静压力在喷嘴收缩发展段内的能量转换过程。由静压曲线可知，流体进入外流场后，受湍流脉动影响，压力曲线出现规律性的上下波动，而后随喷距增加脉动效应减弱，射流轴线压力与环境围压持平，到达冲击平面后，流体在驻点聚积，压力出现回升。动压曲线在喷嘴出口附近表现出了相似的波动特征，而后波动幅度逐渐减弱，与静压曲线相反，在到达驻点时，由于流体流动受阻，动压出现短暂骤降。

2.3.2 喷嘴压降对旋转射流压力场分布的影响

由不同压降条件下外流场压力分布云图可知（见图12a），压降变化并没有明显改变流场中的压力分布特征。压降由10 MPa增加到25 MPa，喷嘴的出口压力由16.61 MPa降低至9.82 MPa，降幅为40.88%，这是由于压降增大，从而降低了流场静压力；而驻点压力由20.95 MPa增加至22.21 MPa，压力增幅为6.30%，主要是由于旋转射流强烈的湍流耗散作用，使得能量在传递至底面时已基本被耗散。由图12b轴线静压力分布曲线可知，随着入口压力的增加，喷嘴收缩发展段的最小静压力逐渐降低，即“负压”效果更明显，在磨料射流过程中可以有效提升磨料颗粒与流体的掺混效果。由轴线动压力分布曲线可知，在喷嘴出口附近，压力曲线的脉动特征随压降的增大而显著增强，这主要是由于周向速度的增加加强了射流的旋流强度，进而加强了射流的湍流脉动特征。在射流下游，旋转射流的湍流耗散效应同样随着压降的增大而增大，增强的湍流脉动使得能量迅速衰减，因此波动的传递距离并无大幅增加。基于此特性，旋转射流更适用于可连续送进并需求大孔眼直径的径向水平井钻进、煤层气水平井造穴、煤矿巷道钻孔卸压等工程应用场景。

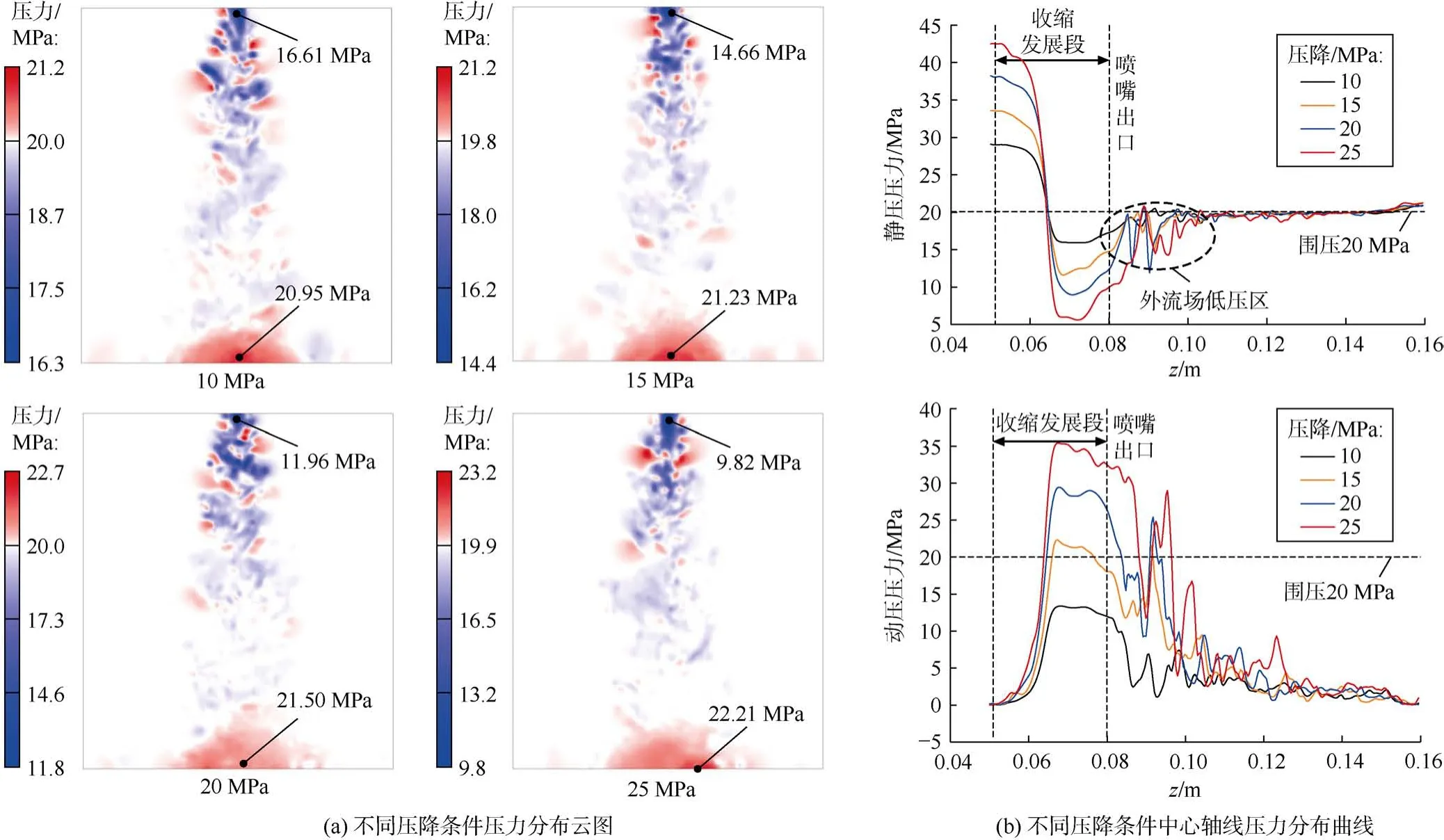
图12 不同压降条件下旋转射流压力分布云图（a）及轴线压力分布曲线（b）

3 结论

旋转射流涡结构的发展大致可划分为 Kelvin-Helmholtz（K-H）不稳定性阶段、过渡阶段和旋转不稳定性阶段。剪切层中各种涡结构的发育，促进了射流内外流体的动量交换，进而加速了射流流体与环境流体的混合，增大了射流扩散面积，但也导致了射流强度的快速衰减。旋转射流的速度分布呈螺旋状，在喷嘴出口附近，旋转效应能够显著增强湍流脉动，尤其是径向湍流脉动，使得速度曲线呈现对称分布；而在射流下游，旋转射流速度衰减的主要原因是旋流效应引起的湍流脉动耗散。旋转射流的压力分布与速度密切相关，受旋流效应的影响，在喷嘴出口附近的压力远低于周围流体围压；在外流场形成了螺旋状分布的射流低压区，涡旋结构发育在低压区边缘。旋转射流形成的低压分布区有利于促进射流与磨料颗粒的混合，对提升磨料射流冲击强度和冲击范围具有重要意义。

在喷嘴出口附近，射流压降对旋转射流涡结构、速度场和压力场的分布有显著影响，通过增大射流压降能够显著增加旋流强度和径向湍流脉动，从而增大射流扩散角和冲击范围。但是由于旋转射流强烈的湍流耗散作用，当喷射距离超过约 9倍无因次喷距后，通过提升压降已不能提高旋转射流的有效冲击距离。综上，旋转射流更适用于需求大孔径的径向水平井钻孔、煤层气水平井造穴和煤矿巷道钻孔卸压等工程场景。

符号注释：

Cdt1，Cdt2，Cμ，Cω——经验常数，无因次；CDES——校准系数，无因次；dw——网格节点距离壁面的距离，m；D——喷嘴直径，m；Dω——交叉扩散项，kg/（m3·s2）；fb——经验混合函数，无因次；——屏蔽函数，无因次；F1，F2——SST模型混合函数，无因次；Gk——湍动能k的产生项，kg/（m·s3）；Gω——比耗散率ω的产生项，kg/（m3·s2）；hmax——网格单元的最大边长，m；hwn——沿壁面的法向单元网格，m；i，j——表示坐标系的不同方向，取值1，2，3；k——湍动能，m2/s2；LIDDES——IDDES的特征长度，m；LLES——LES的特征长度，m；LRANS——RANS的特征长度，m；p——流体压力，Pa；Pk——湍动能生成项，kg/（m·s3）；rdt——延迟因子，无因次；S——应变率张量，s-1；Si——动量守恒方程源项，kg/（m2·s2）；Sk——湍动能自定义源项，kg/（m·s3）；Sω——比耗散率自定义源项，kg/（m3·s2）；t——时间，s；v——流场中相应位置的流体速度，m/s；va——喷嘴出口的平均速度，m/s；v——速度矢量，m/s；x，y，z——空间坐标，m；Yk——湍动能k的耗散项，kg/（m·s3）；Yω——比耗散率ω的耗散项，kg/（m3·s2）；α，β——湍流黏度抑制系数，无因次；ε——耗散率，无因次；Δ——截止尺度，m；κ——冯卡门常数，无因次；μ——流体动力黏度，Pa·s；μt——湍流黏性系数，Pa·s；ρf——流体密度，kg/m3；σk——湍动能k的湍流普朗特数，无因次；σω——比耗散率ω的湍流普朗特数，无因次；Γk——湍动能k的有效扩散率，kg/（m·s）；Γω——比耗散率ω的有效扩散率，kg/（m·s）；υt——运动涡黏性系数，m2/s；ω——比耗散率，s-1；Ω——涡量张量，s-1；∇——哈密尔顿算子。