高速公路纵坡坡长可靠性设计研究

张 航，田 晟，李 明

(1.武汉理工大学 交通学院，湖北 武汉 430000；2.江苏中设集团股份有限公司，江苏 无锡 214000)

0 引言

近年来，由于车辆产业的高速发展，车辆类型在不断丰富的同时也展现出向重型化汽车发展的趋势，重型车辆在我国高速公路交通组成中的占比逐渐提高。在高速公路纵坡路段行驶过程中，由于重型车辆需要克服的道路坡度阻力更大，行驶速度下降更快，因而与小型客车速度差值变大，影响了道路的通行能力及交通安全。若道路自身设计上存在不合理的坡度和坡长组合，会加剧大型车辆爬坡动力性能不足，出现爬坡困难的现象，从而引发一系列交通事故。

为了解决此类问题，国内外学者进行了大量的研究。田冬军等[1]通过对行车中驾驶员的心率和行车速度进行测试,研究了心率和行车速度的变动与纵坡度值的相关关系,分析了此种路段上纵坡度的合理值,并提出在公路线形设计中,不宜出现大于5%的纵坡度值;周荣贵等[2]通过速度折减量与坡长之间的关系曲线,提出了基于运行速度差和满足公路服务水平要求的各级公路最大纵坡坡度与坡长限制值;石飞荣[3]通过对车辆的运动方程、受力、动力性能分析，提出了将最大纵坡分为理想最大纵坡、一般最大纵坡、极限最大纵坡3个等级；庄传仪等[4]根据汽车功率质量比计算模型和试验方法,确定了不同地区、不同公路等级下货车功率质量比,由此建立了最大纵坡坡度、不同纵坡的最大坡长等几何线形设计参数；董忠红等[5-7]建立了重型车辆动力爬坡模型，研究了长大纵坡路段爬坡车速变化规律，结果表明爬坡稳定速度与入坡速度无关，但提高入坡速度会增加稳定坡长，同时基于爬坡车速变化规律给出了坡度、坡长限制建议，为公路路线设计提供参考。

同时为了提高道路安全性，道路交通领域也开始探索对可靠度理论的应用。Navin等[8-12]最先将可靠性理论引入到道路工程中去；东南大学杨晨[13]在学术论文中选取平面和纵断面的6个设计参数进行可靠度计算，得到了不同取值下的失效概率，并对这些参数进行安全性评价，构建了基于可靠度的道路线形安全评价模型；聂瑞红[14]选取合适的平、纵线形组合影响因素，提出了基于曲线前必需视距法的可靠度计算方法与基于层次分析法的平、纵线形组合可靠度分析方法,建立了路线设计指标可靠度与事故指标间的关系。但现有对可靠度的研究缺乏对评价指标在不同梯度范围内的量化讨论，本研究从公路交通安全现状出发，选取高速公路纵坡作为研究对象，讨论纵坡上坡路段影响车辆行车安全的道路条件，引入可靠度理论，建立坡长与坡度的功能函数，运用可靠度理论分析方法计算在不同设计速度对应的最大纵坡坡度条件下,不同坡长供给值的失效概率,得出不同坡长供给值对可靠概率的影响关系，指出存在设计安全隐患的指标取值，并提出高速公路设计中阶梯坡度范围内安全纵坡坡长建议值，为合理确定公路路线纵坡坡度和坡长的组合提供依据。

1 代表车型选取及纵坡坡长计算

1.1 代表车型选取

我国高速公路中小客车和大型车是交通事故中常见的肇事车型,小客车与大型车的事故数相近，但大型车事故伤亡人数却远高于小客车[15]。据资料统计发现，大型车辆交通事故中重型车辆占据主导地位，且伴随有超载、超限等违规现象。经调查国内各载重货车生产企业的销量情况，前三甲分别为一汽、东风、重汽，综合比较，拟选定一汽解放J7牵引车CA4250P77K25T1E5作为代表车型[16]，相关计算参数见表1。

表1 代表车型计算参数

1.2 纵坡坡长计算

车辆在路段上运行，变速箱处于不同的档位，汽车进行加减档时，发动机提供的牵引力不同，车辆的运行加速度也不同，车辆在上坡到达稳定速度前大致呈减速状态，基于此，可通过微积分计算得到坡长的表达式：

(1)

式中,L为纵坡坡长；λ为修正系数,此处取1；g为重力加速度，此处取9.8 m/s2；v1，v2分别为换挡前、后的速度；f为滚动轮胎的阻力系数,高速公路取值为0.01；i为道路纵坡坡度；v为运行速度。

2 纵坡坡长可靠性设计分析

2.1 纵坡坡长可靠度功能函数

依据《公路工程结构可靠性设计统一标准》(JTG 2120—2020)[17]可知，可靠度是指工程结构在规定的时间内，规定的条件下，完成预期功能，取得预期结果的概率。如果结构能够完成预定的功能，则称结构处于可靠状态，反之，则称结构处于不可靠状态。将结构的可靠状态与不可靠状态的临界位置称为极限状态，根据结构到达“极限状态”作为条件，构建相关数学函数式，用以评判结构是否可靠。本研究将可靠度理论引入道路设计中，用失效概率来表示纵坡坡度设计中设计值超出安全范围的部分可能存在的安全隐患。道路设计坡度、坡长能够满足车辆实际运行条件且在车速降至规定容许速度前完成爬坡过程，将其称为安全行驶。在设计速度对应的临界坡度条件下，车辆在纵坡路段保证安全行驶所需要的坡长值称为安全坡长值，道路设计所提供的坡长值称为设计坡长值；当设计值小于安全值便认为设计是可靠的，反之则设计值失效，存在安全隐患。因此，依据以上所述，可将道路纵坡坡长可靠性的功能函数设为:

Z=L-S，

(2)

式中，Z为道路纵坡坡度可靠性功能函数；L为车辆安全行驶所需要的坡长值，可由式(1)计算而来；S为道路设计提供的坡长值。

2.2 可靠度功能函数参数分析

在式(1)、式(2)中，功能函数涉及的变量较多，为了方便研究将坡道入口处的车辆运行速度和坡度作为随机变量进行分析，其余参数作为确定性变量用于求解可靠度。坡度的变化在后续研究中简化成均匀变化，而另一个变量运行速度则通过实地测量获取。为了获取我国不同设计速度下高速公路纵坡入口处车辆行驶速度情况，采用专业的车辆分型统计系统MetroCount5600进行车型划分及速度测量。选取的高速公路调查路段包含3种设计速度(120，100，80 km/h)，调研路段平面线形要求平曲线半径较大或为直线，以减少弯道对于车速的影响，从而保证数据的准确性。将所观测的样本数据进行统计整理后，对异常数据进行剔除。利用统计分析软件SPSS对数据进行单样K-S检验，整理之后的结果如表2所示。

表2 高速公路坡道入口处车辆运行速度K-S检验表

从表2中的检验结果可以看出，120，100，80 km/h 3种设计速度所对应的运行速度统计值精确显著性水平分别为0.847，0.932，0.669，均大于0.05的显著水平值，则认为所观测的样本数据总体即高速公路纵坡坡道入口处车辆运行速度分布服从正态分布。

2.3 纵坡坡长可靠度验证

坡长在纵坡路段交通安全中的作用主要是削弱坡度对于交通安全的不利影响。坡长限制表示满载的载重汽车在一个指定的上坡道上行驶时不致发生不合理减速或减速到允许的范围时的坡道长度。但坡长过长会导致载重货车在爬坡过程中的减速不断积累，从而使得车速过低而诱发事故。因此为了更为准确地把握纵坡坡长设计取值，需要针对不同坡长对车辆安全行驶的失效概率做定量研究。一般认为，在车速降低至容许速度前驶过坡顶是安全行驶。但纵坡坡长的讨论离不开坡度的影响,坡度的增加会使车辆速度下降，加速度增加，使得达到容许速度前驶过的坡长减短,所以只有与坡度相适应的坡长是有利的。而《公路路线设计规范》(JTG D20—2017)[18]中对于不同设计速度条件下的道路纵坡设计仅提供了最大坡度限制及最大、最小坡长限制，如在设计速度为120 km/h时,对应于最大纵坡坡度3%的最大坡长为900 m。但实际设计中往往有些案例为规避标准规范约束，采用略小于最大纵坡坡度却远大于最大坡长的设计，如纵坡坡度取2.9%，坡长取1 800 m，显然，这样的设计符合规范，但明显会带来安全隐患。这种现象从一个侧面说明,对线形设计的安全性缺乏量化的评价方法,往往会影响高速公路的快速性，甚至导致交通事故多发。基于此点，依据可靠度理论对不同设计速度下不同坡度及坡长进行分析，以车辆爬坡速度折减至容许速度作为安全极限条件，判断设计指标是否失效。《规范》中高速公路不同纵坡的最大坡长、公路纵坡最小坡长及容许速度如表3、表4所示。

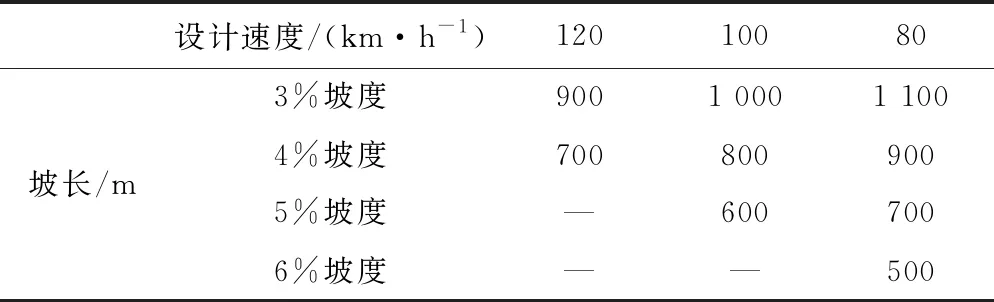
表3 不同纵坡的最大坡长

表4 公路纵坡最小坡长及容许速度

此外，《规范》中设计速度为120，100，80 km/h 的高速公路最大纵坡设计指标值分别为3%，4%，5%，在遇到地形困难或其他特殊情况限制时，经由技术和经济等多方面论证，最大纵坡度坡可增加1%。但由于极限最大纵坡的选用条件苛刻，一般不用于直接指导设计，后面不讨论其指标失效概率问题。

式(1)阐述了纵坡坡度与坡长间的计算关系，其中坡长的计算公式是含有积分的表达式。因此，考虑到蒙特卡洛模拟法[19]是以概率和统计理论方法为基础的一种计算方法，是使用随机数来解决计算问题的方法，可以用来求解含积分的坡长功能函数可靠度。通过MATLAB软件编程，可以抽样模拟计算不同设计速度、设计坡度在不同坡长供给值下的失效概率。蒙特卡洛模拟法计算纵坡坡长可靠度的基本步骤如下：

(1)定义抽样次数N，输入纵坡坡度i，坡长供给值S。现以测量路段G42高速公路为例(上行方向)，以该路段上春运期间的交通量来确定抽样次数N。2019—2021年春运期间该路段交通流量如表5所示。

表5 2019—2021年春运期间交通量

因此，根据交通量拟定抽样次数N=72万次。

(2)入坡速度V1由MATLAB软件根据表2中的已知分布随机产生，由式(1)结合表1计算车辆达到坡道允许速度所需的坡长,即为安全坡长值。

(3)根据式(2)，记录满足L-S>0，即Z>0的次数，并除以抽样次数N，计算可靠度。

由式(1)、式(2)根据蒙特卡罗法计算当设计速度分别为120，100，80 km/h，对应最大纵坡坡度分别为3%，4%，5%时，道路纵坡的可靠度概率值与坡长供给值的关系整理如图1、表6所示。

表6 不同设计速度下坡长供给值的可靠度计算结果

根据图1可以发现，在不同设计速度对应最大纵坡坡度条件下，不同坡长供给值对可靠概率的影响，表现出随着坡长的增加纵坡可靠概率逐渐下降；而对于坡长供给值相同的条件下，纵坡可靠概率随着坡度的增大而大幅度下降。这表明在上坡路段，坡度的增加会使车速快速降低，长距离的坡长和较大的坡度都会使得该路段安全可靠概率降低。

图1 不同坡长供给值的爬坡可靠度概率分布

由表6可知，设计速度120 km/h，纵坡坡度为3%的高速公路，在坡长取最大值900 m时，失效概率为4.419%，可靠概率为95.581%；设计速度为100 km/h，纵坡坡度为4%的高速公路，在坡长取最大值800 m时，失效概率为13.445%，可靠概率为86.555%；设计速度为80 km/h时，纵坡坡度为5%的高速公路，在坡长取最大值700 m时，失效概率为25.126%，可靠概率为74.874%。

文献[20-21]在结合可靠度研究行车视距和弯道超高时将《公路工程结构可靠性设计统一标准》(JTG 2120—2020)引入其计算模型，得出合理计算结果。因此，本研究中对道路纵坡坡长设计的可靠度要求也参考该标准中对路面结构目标可靠度的规定，如表7所示。

表7 不同安全等级对应的可靠度

因此对于结构安全等级为一级的高速公路来说，目标可靠度值需要大于95%。而当设计速度为100，80 km/h对应最大纵坡为4%，5%时，可靠概率均小于95%，达不到一级安全结构等级,表明现行路线设计规范对于不同设计速度的高速公路最大纵坡坡长设计值800，700 m可靠性不足，需要进一步量化研究道路可靠度与坡长的关系。根据前述的计算结果，以设计可靠度大于95%为满足条件，得到不同设计速度下对应最大坡度所需的最大安全坡长值，并列于表8。

表8 高速公路纵坡安全坡长计算值

2.4 纵坡安全坡长建议值

由于在实际纵坡路段设计时一般不会采用最大坡度和最大坡长的极限组合，因此需要进一步了解在不同设计速度下，不同坡度条件值和不同坡长供给值与纵坡路段行车安全可靠度之间的详细分布关系，仍采用蒙特卡洛法对不同坡度条件值下不同坡长供给值的可靠度进行独立计算，参照上节中结构安全等级，将可靠度概率大于95%的坡长供给值作为安全坡长建议值，由此得出阶梯坡度范围内坡长的限制要求。同时为了研究方便,当设计速度为120，100，80 km/h时，将纵坡坡度取最大坡度作为上限，最大坡度下浮1%作为下限值。道路纵坡可靠度概率随坡长供给值变化趋势如图2所示。

图2 不同设计速度下，不同坡长值下坡度可靠度概率分布

依据图2所示,在设计速度分别为120，100，80 km/h时，将可靠度大于95%的坡长供给值作为建议值，整理如表9所示。

不难发现，在相同坡长供给值条件下，纵坡可靠度概率随着坡度的增大而降低。由图2(a)可知，当纵坡坡度为2.2%时，可靠度概率随坡长供给值的变化较缓，其原因可能是2.2%坡度接近代表车型在该路段上行驶不限坡长的最大纵坡坡度；结合表9，当纵坡坡度为3%，4%时，安全坡长建议值分别为900，700 m，与表8中的计算结果一致；当纵坡坡度为5%时，安全坡长建议值为500 m,略小于表8所示的550 m;对于代表车型,安全坡长建议值小于规范值,表明规范对于代表车型而言，出现了“车不适应路”的问题，这也从侧面说明在进行纵坡设计时，应充分考虑主导车辆的影响因素。随着工业化的发展，车辆载重越来越大，而车辆大型化会导致某些可能原本符合要求的道路设计的失效概率上升，增加了纵坡路段中出现交通阻塞甚至交通事故的可能性。因此，基于可靠度分析纵坡坡度、坡长指标对于指导实际纵坡设计有一定参考价值，有利于提高道路安全性。同时,路线设计中需要针对实际的主导车型进行设计，对于规范中的设计值应灵活应用，避免死板地遵循规范，避免对规范进行透支使用。

表9 不同坡度下安全坡长值

2.5 工程实例

现以3条封闭高速公路为例，标号1-5、标号6-10、标号11-15分别对应设计速度为120，100，80 km/h的路段。根据此三路段1 a内所发生的事故，统计该路段中所有纵坡坡度大于2%的上坡路段的年里程交通事故率，将事故率大于10次/km的路段作为事故频发路段，列于表10。同时计算不同纵坡路段上坡设计取值的失效概率，分析事故率与失效概率间的关系，讨论爬坡路段设计值的安全合理性。

表10 统计事故频发路段纵坡设计指标

由表10中结果可以看出，纵坡坡度值在设计时避免采用规范限定的最大值，但路线上坡中仍存在不少事故频发路段,所统计的15处坡度大于2%的上坡路段中，事故频发路段有6处。不难发现，同一设计速度下坡长相近时坡度值越高，行车安全隐患越大；坡度值相近条件下坡长越长，行车安全隐患越大。仍采用蒙特卡洛法对表10中统计的纵坡路段的坡长设计值的失效概率进行计算，分析其可靠性。统计路段纵坡设计值失效概率计算结果如表11所示。

由表11可知，事故频发路段的设计值失效概率较高，且纵坡坡度大于3%的路段多为事故频发路段，其设计值虽然满足规范要求，但可靠程度较低，例如路段7设计坡度值及坡长值均低于规范最大值，但其设计值可靠度概率为73.31%，低于表7所示的一级结构安全等级对应的95%可靠度，因此建议采用表9中不同坡度下安全坡长建议值，限制因坡长过长而加强坡度对于交通安全的影响作用，提升设计指标的可靠度。但是可靠度是基于概率学对事物的安全性展开讨论，纵坡失效概率计算值高，并不代表该纵坡路段会发生事故，例如路段10、路段14的设计值失效概率分别为12.95%，10.42%，但却不是事故频发路段。然而，统计的事故频发路段的失效概率计算值都大于10%，这表明失效概率在一定程度上可以反映不良道路线形指标与交通事故间存在着关联性。因此，对纵坡设计展开可靠度分析能够量化道路安全程度，为道路线形指标设计提供一些建议和参考，具有一定的工程实际意义。

表11 统计路段纵坡设计值失效概率

3 结论

(1)根据建立的坡长与坡度可靠度功能函数，对现行规范的最大坡长进行可靠度分析，发现其对于不同设计速度下的高速公路最大纵坡坡长指导值800，700 m可靠性不足，并根据安全等级一级的可靠性要求计算出相应的坡长值。当设计速度为120 km/h 时，对应最大纵坡坡度为3%的安全坡长建议值为900 m，与规范一致；当设计速度分别为100，80 km/h时，对应最大纵坡坡度为4%，5%的安全坡长建议值分别为700，500 m，都小于规范值。同时将可靠度概率大于95%的坡长供给值作为安全坡长建议值，得出阶梯坡度范围内坡长的限制要求，为设计人员进行纵坡与坡长组合设计时提供一定的参考。

(2)现有规范中没有对纵坡坡长可靠度作出明确规定，本研究以《公路工程结构可靠性设计统一标准》(JTG 2120—2020)为依托求解可靠度函数并结合相关实例，结果表明对纵坡设计展开可靠度分析能够量化道路安全程度，从而为高速公路纵坡指标设计提供一些建议和参考，具有一定的工程意义。但同时，纵坡坡长可靠度如何规定也是今后需要研究的问题。