交通信号协调控制的方案过渡研究
2022-08-25丁海龙
丁海龙
(连云港杰瑞电子有限公司,江苏 连云港 222000)
交通信号协调控制作为提高出行效率的有效手段,对维护城市道路交通秩序安全的意义重大,越来越受交通管理者重视,近年来全国各地广泛应用。在协调控制中,配时变化、时钟调整、紧急优先等情况出现时,通过延长或缩短周期绿信比,实现相位差平稳、连续过渡调整的过程称为方案过渡[1-8]。以传统方案过渡方法及其衍生算法[9]为代表的平滑过渡算法,有较多研究成果,Lieberman等[10]提出过一种以过渡持续时间最短为目标的RAST(Rapid Signal Transition Algorithm)过渡算法;宋现敏[11]提出过基于不同过渡转换时间建立一次、二次、三次平滑过渡方法;谭伟丽[12]提出过一种面向活跃相位的干线协调信号控制配时方案过渡算法;郭海峰等[13]提出过以最佳相位差调整量为依据的快速平滑过渡方法;树爱兵等[14]提出过基于周期时长调整范围与绿灯时间分配策略的协调控制过渡方法。上述几种方法虽然能解决一些平滑过渡算法在过渡时长波动性较高的缺陷,但在移植信号机实战应用时,仍存在两个典型问题,一是未考虑延长与缩短策略内在关联,决策单一;二是未考虑协调及通行对绿信比需求,分配不均。
1 两级决策模型
1.1 过渡调整判定
假定公共周期C,阶段总数n,协调相位差O,阶段i的基础时长ti_base,则周期切换时刻的期望相位差
(1)
式中:k为协调阶段号。
周期切换时刻与统一时钟基准点的偏差Tlocal,则实际相位差
Qreal=mod(Tl0cal,C)
(2)
若Oreal=Oexpect,无需过渡调整,否则,需要过渡调整。
1.2 关联调整量
需要过渡调整时,分以下两类情况讨论
若Oreal Tadj_plus=Oexpect-Oreal (3) Tadj_minus=C-Oexpect+Oreal (4) 若Oreal>Oexpect,缩短调整量及关联的延长调整量分别为 Tadj_minus=Oreal-Oexpect (5) Tadj_plus=C-Oreal+Oexpect (6) 上述两种情况中,延长与缩短调整量在[1,C-1]内的模值之和等于周期值,即 Tadj_plus+Tadj_minus=C (7) Tadj_plus∈[1,C-1]与Tadj_minus∈[1,C-1]互称为关联调整量。 延长调整所需过渡周期数 Rtsplus=[Tadj_plus/ΔCtunit_plus] (8) 式中:ΔCtunit_plus为周期最大可延长秒数。 缩短调整所需过渡周期数 c (9) 式中:ΔCtunit_minus为周期最大可缩短秒数。 依据互为关联调整量的特性,缩短过渡调整总过渡周期数的延长表达为 Rtsminus=[(C-Tadj_minus)/ΔCtunit_minus] (10) 以公共周期120 s为例,分别对单周期延长和缩短调整时长占周期5%、15%、25%的总过渡时长进行对比研究,其中左侧竖线区域表示,在当前Tadj_plus下,延长过渡调整所需的周期数更小;右侧细点形成的横线区域表示,在当前Tadj_plus下,缩短过渡调整所需的周期数更小;中间粗黑区域表示,在当前Tadj_plus下,延长与缩短过渡调整所需的周期数相等。同时,随着Tadj_plus的增加,延长所需过渡调整周期数逐渐阶梯增加,缩短所需过渡调整周期数逐渐阶梯下降;阶梯宽度与单周期调整量正相关。 延长过渡调整总过渡调整时长 Ttotal_plus=Rtsplus×C+Tadj_plusRtsplus>0 (11) 缩短过渡调整总过渡调整时长 Ttotal_minus=Rtsminus×C-Tadj_minusRtsminus>0 (12) 依据互为关联调整量的特性,缩短过渡调整总过渡调整时长的延长表达为 Ttotal_minus=[(C-Tadj_plus)/ΔCtunit_minus]×C-(C-Tadj_plus)Rtsminus>0 (13) 如图2所示,同样以公共周期120s为例,分别对单周期延长和缩短调整时长占周期5%、15%、25%的总过渡时长进行对比研究。其中左侧竖线区域表示,在当前Tadj_plus下,延长过渡调整所需的总过渡时长更小;右侧细点形成的横线区域表示,在当前Tadj_plus下,缩短过渡调整所需的总过渡时长更小;中间粗黑区域(交点)表示,在当前Tadj_plus下,延长与缩短过渡调整所需的总过渡时长相等。单周期延长调整值不变时,单周期缩短调整值增加,交点左移,延长优势区减少,缩减优势区增加;单周期缩短调整值不变时,单周期延长调整值增加,交点右移,延长优势区增加,缩减优势区减少。 上述对比分析结果表明,不同条件下,延长与缩短调整策略的优势区间并不相同,挑选合适的调整策略,有利于降低过渡调整对交通波动影响。因此,本文设计了基于总过渡调整时长较小及与调整前后周期中值偏离度较小优化目标的两级过渡决策模型。 模型第一级,侧重调整速度,总过渡调整时长差异过大时挑选较小的过渡调整策略;模型第二级,侧重方案波动,总过渡调整时长差异在一定范围内时,选择与调整前后周期中值偏离度较小的过渡调整策略。 以延长与缩短两种过渡调整策略的总过渡调整时长差值的绝对值与切换后周期时长之比构建TS指标,即 (14) 若TS>1,延长与缩短过渡调整策略的总过渡调整速率差异明显,选择min{Ttotal_plus,Ttotal_minus}对应的调整策略;否则,调整速率相差不大,考虑减少方案过渡波动,用单周期过渡调整时长与调整前后周期中值差值的绝对值表示偏离度,令切换前的周期Cper,则 Cmid=(Cper+C)/2 (15) 延长过渡调整单周期时长与中值偏差的绝对值 (16) 缩短过渡调整单周期时长与中值偏差的绝对值 (17) 若Devplus≤Devminus,选择延长过渡调整策略;否则选择缩短过渡调整策略。 决策模型输出延长过渡调整策略时,优先延长协调阶段绿灯,再对非协调阶段逐秒均匀延长,周期及阶段的延长调整时长不可超过单周期及各阶段最大可延长秒数。 令单周期剩余所需调整时长初始值为 (18) 优先延长协调阶段绿灯,即协调阶段时长 (19) 式中:Δtk_plus为协调阶段k最大可延长秒数,tk_up为协调阶段k的上限时长。 更新单周期剩余所需调整时长 (20) 继续循环逐秒分配至各非协调阶段,直至该剩余调整时长为0; 决策模型输出缩短过渡调整策略时,优先对非协调阶段逐秒均匀缩短,再缩短协调阶段绿灯,周期及阶段的缩短调整时长不可超过单周期及各阶段最大可缩短秒数。 令单周期剩余所需调整时长初始值为 (21) 优先对非协调阶段逐秒分配缩短,非协调阶段最大总缩短消耗时长 (22) 式中:Δti_minus为非协调阶段i最大可缩短秒数。 更新单周期剩余调整时长 (23) 若ΔCtreal>0,继续通过延长协调阶段绿灯时长消耗该调整时长 tk_base=tk_base-ΔCtreal (24) 依托杰瑞自研信号机在环仿真算法验证系统,搭建小型协调路网,验证两级过渡决策模型与绿信比分配方法运行效果。从左到右,分别为路口1至路口3。 各路口配置信息,见表1。 (1)TS指标决策 路口1的TS=1,总过渡调整速率相差不大,进一步基于Dev指标决策; 路口2的TS=2,总过渡调整速率差异明显,选择更快的延长调整策略; 路口3的TS=1,总过渡调整速率差异明显,选择更快的缩短调整策略。 (2)Dev指标决策 仅路口1需要执行Dev指标决策。其延长过渡调整单周期时长与中值偏差的绝对值Devplus=25,缩短过渡调整单周期时长与中值偏差的绝对值Devminus=11,即Devplus>Devminus,则路口1选择缩短过渡调整策略。 (3)过渡调整策略输出 各路口的过渡调整策略输出,如表2。 表1 路口配置方案 表2 各路口过渡调整策略 (1)以路口2为例,展示延长分配过程 ①初始ΔCtreal=20; ②优先延长协调阶段时长 协调阶段时长t1_base=44,更新ΔCtreal=1; ③继续均匀延长非协调阶段时长 第一轮,{t2_base,t3_base,t4_base}修正为{28,38,28},更新ΔCtreal=2; 第二轮,{t2_base,t3_base,t4_base}修正为{28,40,28},更新ΔCtreal=0; ④最终,{t2_base,t3_base,t4_base}修正为{44,28,40,28},过渡周期ΔCtreal=140。 (2)以路口1为例,展示缩短分配过程 ①初始ΔCtreal=16; ②优先均匀缩短非协调阶段时长 第一轮,{t1_base,t2_base,t4_base}修正为{32,22,22},更新ΔCtreal=7; 第二轮,{t1_base,t2_base,t4_base}修正为{30,20,22},更新ΔCtreal=3; ③继续缩短协调阶段时长 协调阶段时长t3_base=32,更新ΔCtreal=0; ④最终,{t1_base,t2_base,t3_base,t4_base}修正为{30,20,32,22},过渡周期Ctreal=104。 本文深入研究出延长与缩短两种过渡调整策略在总过渡周期数和总过渡调整时长方面的规律,构建包含表征调整速度的TS指标和表证周期中值偏离度的Dev指标的两级轻量化决策模型,设计符合协调需求与通行需求的绿信比均匀分配方案。并依托杰瑞自研信号机在环仿真算法验证系统,验证了决策模型及绿信比分配方法的可操作性和实用性,解决了实践中常见的决策单一和分配不均的两个典型问题。1.3 总过渡周期数
1.4 总过渡调整时长
1.5 TS与Dev两级决策模型
2 绿信比分配
2.1 延长调整
2.2 缩短调整
3 算例分析
3.1 算例背景
3.2 模型决策
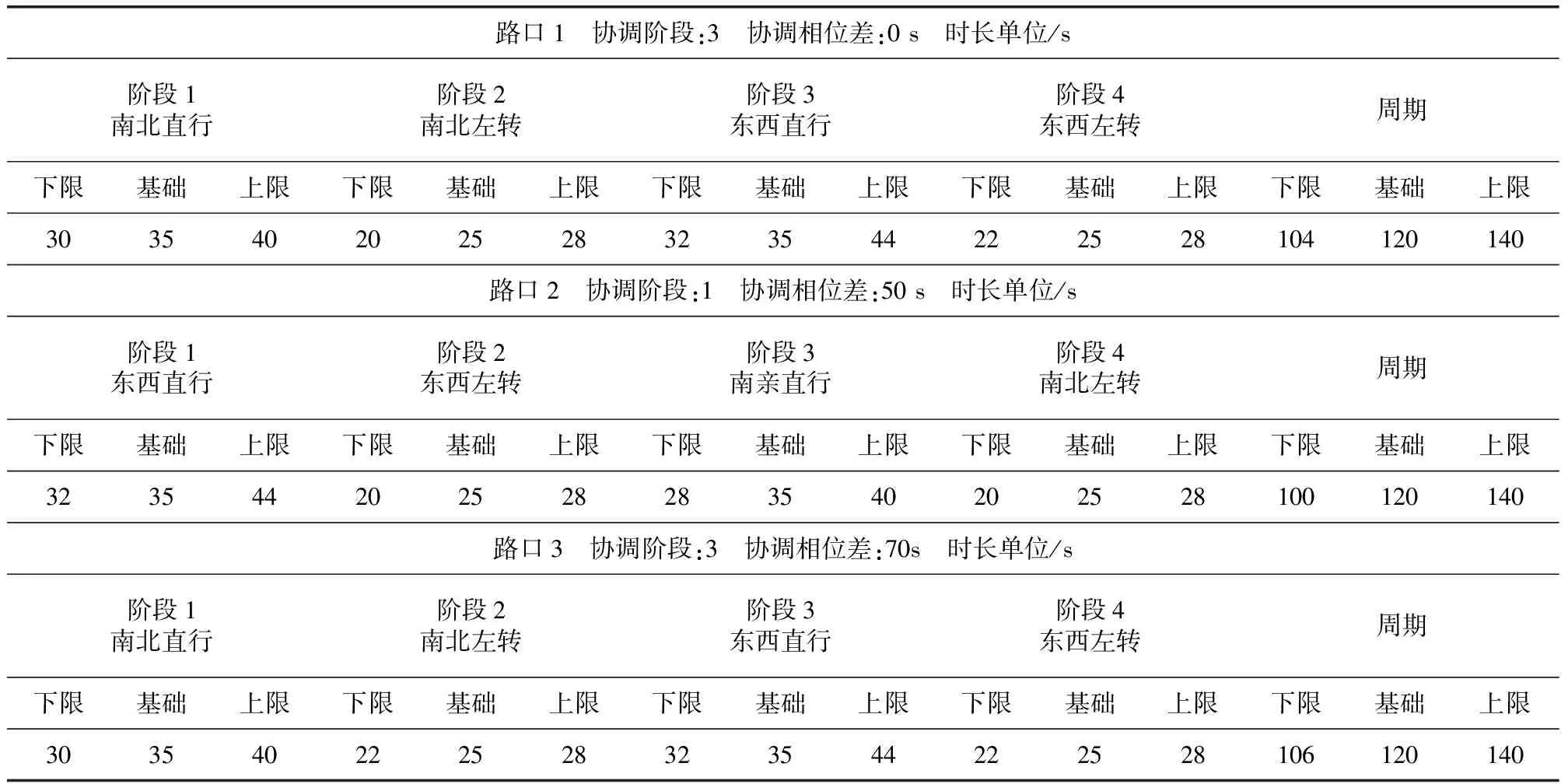
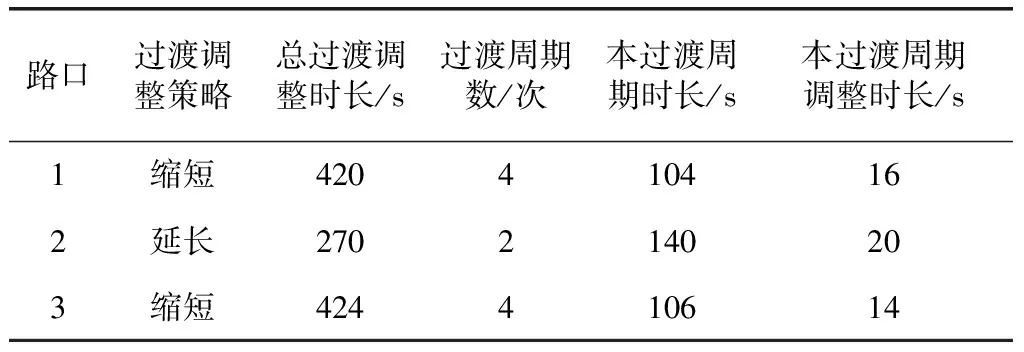
3.3 绿信比分配
4 结 语
