不同曲线半径下弯桥抗倾覆稳定性分析

束文阳，纪海龙

(1.安徽省交通规划设计研究总院股份有限公司，安徽 合肥 230088；2.公路交通节能环保技术交通运输行业研发中心，安徽 合肥 230088)

1 抗倾覆机理

周所周知，单支座无法对梁体扭转变形产生约束，同一个桥墩的多支座可以对扭转变形的扭矩起到双重约束。正常情况下，对于不同曲线半径下的箱型梁桥各支座均应处于受压状态。然而，当上部荷载超限或偏载严重时，将产生较大的倾覆力矩，此时偏载另一侧的支座会逐步脱空，直到只剩一个有效支座时，便失去对箱梁的抗扭约束，当所有桥墩支承均失去对扭转变形的约束的时候，此时倾覆达到临界状态。随着扭转变形的进一步发展，梁体将发生倾倒、垮塌，连带支座和下部结构损毁。

有关桥梁抗倾覆稳定性的计算方法一直以来便存有争议，老版《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTG D62—2004)中由于没有关于桥梁抗倾覆稳定的相关计算要求，因而目前在运营的公路桥梁当中，大多没有考虑过桥梁倾覆问题。随着社会的不断发展，荷载等级的进一步提升，桥梁倾覆问题便开始大量涌出，桥梁抗倾覆稳定也得到了进一步的重视，《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTG D62—2012征求意见稿)(以下简称混规2012征求意见稿)首次给出了公路桥梁抗倾覆验算的计算方法及公式[4]，但仍有争议。混规2012征求意见稿中针对中小跨径桥梁提出采用整体式断面来验算桥梁上部结构的抗倾覆稳定性，桥梁抗倾覆稳定性应满足公式(1)要求

(1)

式中：γqf为抗倾覆稳定系数；Ssk为标准组合下使桥梁发生倾覆的汽车荷载(含冲击作用)产生效应(效应)；Sbk为标准组合下抵抗桥梁上部结构倾覆的作用效应(抗力)。

混规2012征求意见稿中关于桥梁抗倾覆计算的类型共包含两种，一种是正交桥梁和斜交角小于30°的斜交桥梁，另一种则是曲线桥。对于曲线桥，当中墩支承均位于桥台或分联墩曲线外侧支承连线的内侧时，倾覆轴线即为桥台曲线外侧支承连线；当跨中桥墩支承均位于桥台曲线外侧支承连线外侧时，倾覆轴线即是某个桥台或分联墩曲线外侧支承和中墩支承的连线。上部结构抗倾覆稳定性系数计算采用公式(2)

(2)

式中：qk为车道荷载中均布荷载；Pk为车道荷载中集中荷载；u为冲击系数；RGi为恒载各支座的支反力；xi为各个支座到倾覆轴线的垂直距离；e为移动活载车道线与倾覆轴线所围成的阴影部分面积；Ω为移动活载车道线与倾覆轴线最大垂直距离。

参考《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTG 3362—2018)(以下简称混规2018)规定，桥梁的抗倾覆稳定性验算采用“抵抗力矩≥抗倾覆稳定性系数×效应力矩”的型式。按各作用的标准组合计算时，桥梁抗倾覆稳定性应符合以下要求

(3)

式中：∑Sbk,i为使上部结构稳定的效应设计值；∑Ssk,i为使上部结构失稳的效应设计值；li为脱空支座与有效受压支座的支座的距离；RGki为恒载标准组合作用下，按全部支座受压的支承体系来计算确定的第i个桥墩处脱空支座的支座反力；RQki为可变荷载标准组合作用下，按全部支座受压的支承体系计算确定的第i个桥墩处脱空支座的支座反力，考虑冲击系数的汽车荷载按各脱空支座对应的最不利布置型式取值[5]。

混规2012征求意见稿中将梁体视为刚体，以车道荷载来计算倾覆力矩，以成桥状态下恒载支反力来计算抗倾覆力矩。桥梁在倾覆过程中梁体的结构变形是刚体和扭转运动的结合，显然混规2012征求意见稿中的计算方法是一种简化处理，其次，箱梁按照倾覆轴线切割后各力矩的求解也变得复杂。混规2018将扭转因素考虑进来后，通过支座抗扭抵抗矩与倾覆力矩的比较来计算抗倾覆稳定性，这更为合理，计算也变得简单。但是，各力矩中的力臂为脱空支座与受压支座之间的距离，是个定值，且条文说明中认为箱梁桥处于倾覆临界特征状态时，每个桥墩都存在一个受压支座，即相当于倾覆轴线为各有效支座的连线，与桥梁轴线曲率并没有关系。综上，桥梁倾覆是一个相当复杂的过程，国内外对于抗倾覆的验算方法和要求也不尽相同，现依据混规2018来进行有限元建模计算分析。

2 建模计算

2.1 结构尺寸

以互通立交匝道桥中最为常见的4×20 m一联单箱单室普通钢筋混凝土现浇箱型梁桥为例，现浇箱梁顶板宽度为850 cm，底板宽度为450 m，悬臂长度为200 cm，梁高为150 cm。

2.2 支座布置

考虑匝道桥在被交路中分带落墩或其他常见桥下空间限制因素等情况，中墩采用一个或多个独柱墩，即单支座，两侧其余墩台采用双支座，支座中心距350 cm，典型支座布置示意如图1所示，图中数字为支座编号。

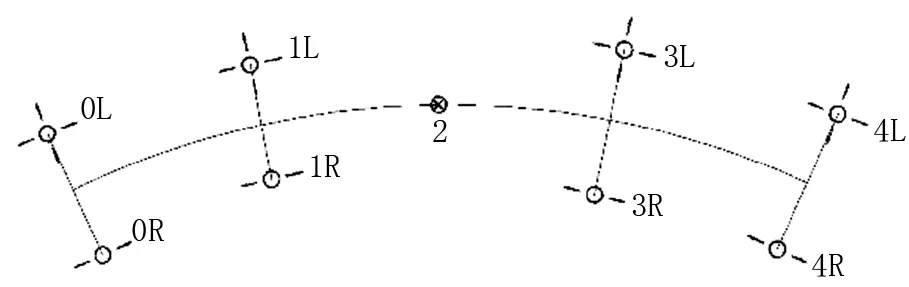
图1 支座布置示意图

2.3 模型建立

采用桥梁博士V4.4.1有限元软件进行建模计算，选用最新的2018公路规范，定义运营阶段抗倾覆稳定性分析。按左、右各横向偏移2.35 m进行纵向移动荷载的加载，分别计算左倾(曲线外侧)和右倾(曲线内侧)抗倾覆稳定系数。计算模型如图2所示。

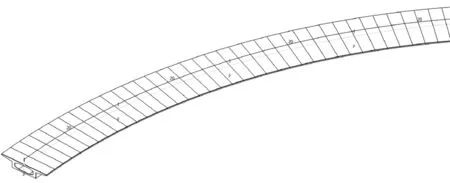
图2 抗倾覆验算模型

3 稳定性分析

3.1 计算结果

根据主梁轴线曲线半径及独柱墩数量的不同，共分六个计算工况。

表1 计算工况一览表

在拟定的验算条件下桥梁上部结构抗倾覆稳定系数的计算结果汇总如下。

表2 抗倾覆稳定性系数

3.2 统计分析

(1)一个独柱墩情况下，曲线半径对抗倾覆稳定系数的影响

控制独柱墩数量不变，均按2#墩采用单支座，其余墩台采用双支座，即对工况1至工况4的计算结果进行统计分析，箱梁外倾和内倾的抗倾覆稳定系数随弯桥曲线半径变化分别如图3和图4所示。

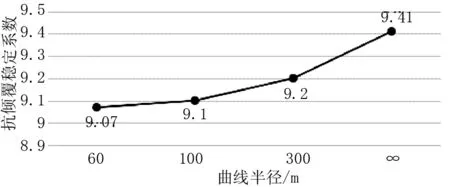
图3 抗倾覆稳定系数(外倾)

图4 抗倾覆稳定系数(内倾)

由图可得出。

①在不同的曲线半径下箱梁内倾的抗倾覆稳定系数始终大于外倾，即对于弯桥而言，箱梁的横向倾覆更容易发生在曲线外侧。

②外倾的抗倾覆稳定系数随曲线半径的增大而提高，而内倾的抗倾覆稳定系数随半径的增大而降低。结合(1)即曲线半径越大箱梁抗倾覆稳定系数的最小值是增大的。这相较于常规理解相悖，究其主要原因，是计算方法不同[6]。新规范中采用的稳定效应与失稳效应的计算力臂为失效支座与有效支座的支座中心距，而不是支座到倾覆轴的距离。

③按新规范的计算方法，不同曲线半径下弯桥内、外侧抗倾覆稳定系数有一定变化，但差值并不大，曲线半径对抗倾覆稳定性并不敏感。

④对于一联仅采用一个独柱墩的弯桥来说，在不同的曲线半径下，在设定计算条件下，抗倾覆稳定系数始终大于2.5，满足混规2018抗倾覆稳定性要求。

(2)曲线半径相同的情况下，独柱墩数量对抗倾覆稳定系数的影响

控制曲线半径相同，独柱墩数量不同，即对工况4至工况6的计算结果进行统计分析，箱梁抗倾覆稳定系数随独柱墩数量变化图如下。

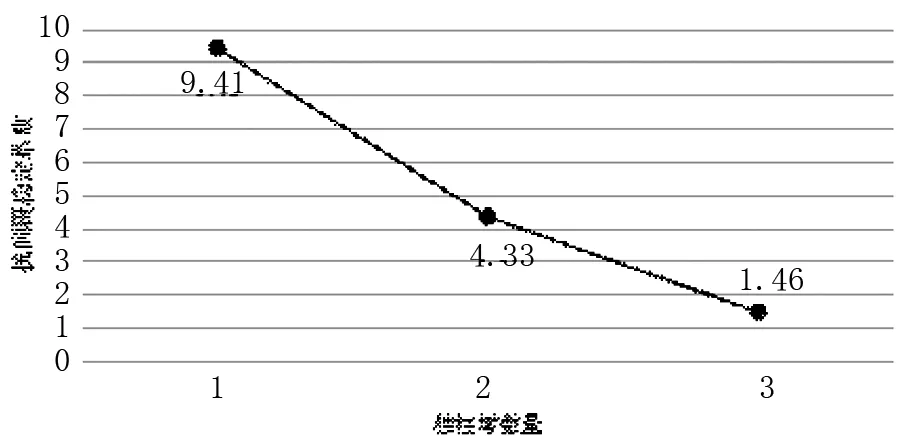
图5 抗倾覆稳定系数

由上图可得出：抗倾覆稳定系数随独柱墩数量的增加而有较大幅度的下降，当一联含有2个独柱墩时，抗倾覆稳定性已经没有太多的富余，当一联含有3个独柱墩时，抗倾覆稳定性不满足规范要求。这一结果也验证了交通运输部2021年2月发布的《公路危旧桥梁排查和改造技术要求》中的有关规定。《公路危旧桥梁排查和改造技术要求》规定：同一联中连续3个及以上桥墩均为独柱墩时，该联不再进行结构验算，应进行改造提升，少于3个独柱墩的情况应进行抗倾覆稳定性验算。

4 结 论

(1)弯桥曲线外侧抗倾覆稳定系数小于内侧，对于单车道的匝道桥，若考虑右侧硬路肩不行车，左转匝道相对而言对抗倾覆更有利，但若桥梁较宽或考虑特殊情况下硬路肩行车，右转匝道相对而言对抗倾覆更有利。即对于弯桥靠曲线内侧行车更不容易发生倾覆。

(2)按新规范计算出的抗倾覆稳定系数对曲线半径并不敏感，曲线半径越小，抗倾覆稳定系数越小。

(3)一联存在连续3个及以上独柱墩的桥梁具有极大的倾覆风险，在设计过程中应该严格禁止，既有桥梁应及时加固；对于一联存在连续2个独柱墩的情况应当加强验算，设计宜避免，既有桥梁宜及时加固。

(4)对于一联仅设置一个独柱墩的弯桥来说，抗倾覆稳定性一般情况下能够满足规范要求，在设计中可以结合抗倾覆验算结果灵活使用，没有必要为了避免独柱墩而强行使用多支座或大跨径。