基于脉冲均衡输出的步进电动机多轴向联动控制
2022-08-25於立峰胡凯波顾范华夏志凌
於立峰,胡凯波,顾范华,夏志凌
(1.浙江浙能兰溪发电有限责任公司,金华 321100; 2.浙江浙能电力股份有限公司,杭州 311200)
0 引 言
随着计算机技术与微电子技术的发展,步进电动机作为机电一体化的执行元件,具有转子惯量低、精准度高、控制操作简便以及误差小等优点,被广泛应用于各个行业的自动化控制系统中的定位与定速[1]。近年来,计算机数控机床的发展以及各种机器人的研发,对步进电动机定位精度以及响应速度的要求有所提升,单轴向的步进电动机已经无法满足各种高精度的要求。多轴向集中控制步进电动机逐渐成为研究的热点。但是,多轴向集中控制方法中最大的弊端是无法实现联动,这主要是因为脉冲不均匀而导致的误差较大。文献[2]提出基于模型变换的步进电动机控制方法,虽然提高了步进电动机的控制精度,但是受外界干扰影响较大,步进电动机脉冲存在较大波动,控制误差较高;文献[3]提出基于外差激光干涉的步进电动机控制方法,采用外差激光干涉步进电动机的脉冲信号,虽然具备一定的脉冲控制性能,但是多轴联动控制效果差,无法实现理想的控制效果;文献[4]分析的磁通反作用电机控制方法可降低步进电动机的能耗,具有节能环保的效果,但是灵敏性较差,控制时间较长。
基于以上缺陷,本文研究了一种智能化步进电动机多轴向集中控制方法,集中控制多轴向的步进电动机,使其可达到加减速、细分以及电流负反馈的功能,精准度更高,更适应于各种高要求的机电一体化设备中。
1 控制方法的设计
1.1 步进电动机多轴向集中控制过程分析
图1为智能化步进电动机多轴向集中控制总体结构图。该控制结构包括8254定时计数芯片、DSP控制系统、逻辑综合电路、DA转换、功率驱动电路与过流检测6个部分。该结构选取TI公司的TMS32LF2812芯片作为DSP控制系统的核心,多轴向步进电动机的相序信号、PWM脉冲、细分值数字信息、DA转换的片选信号均由DSP控制系统进行发送,DSP控制系统还负责与外部进行通信与信号的细分,并通过外界的通信指示发送控制信号至多个轴向步进电动机。
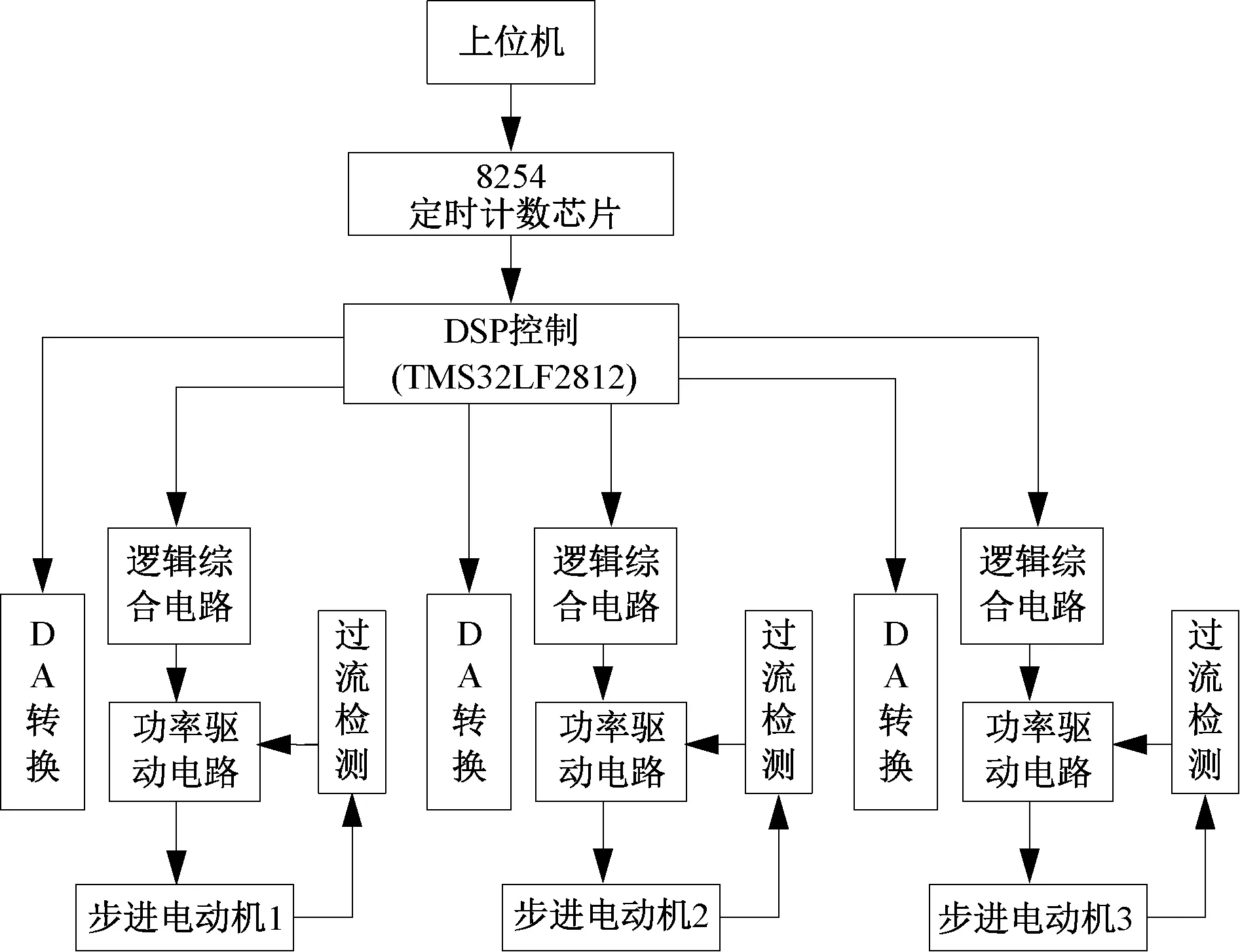
图1 智能化步进电动机多轴向集中控制流程图
逻辑综合电路利用可编程逻辑器件通过合成相序信号与PWM波信号获取新具有斩波的相序信号。DA转换部分利用双通道的8位DA芯片将DSP发送的步进电动机两相细分值数字信号转换成细分功能所需的细分值模拟量,利用DSP发送的片选信号与写信号选择转换成几相细分值[5]。过流检测部分的主要功能为电流保护,将获取的采样电阻中电压值与基准电压相比,采样电阻中电压值高于基准电压时则系统自动停止工作,保证相电流不超过基准电压,保护电机与控制系统[6]。选取两个H桥的高集成度步进电动机控制专用驱动芯片作为系统的功率驱动部分主要组成,并在功率驱动部分合成DA转换部分所发送的细分值模拟量,获取脉冲[7]。但是由于脉冲无法均衡输出,故无法实现多轴向联动控制。
1.2 脉冲均衡设计
通常情况下智能化步进电动机的最高起动速度低于最高运行速度,因此无法按照最高运行速度起动电机。异步电机具有旋转系统的惯性,因此无法在快速运行至接近终点时立即停止与锁定[8]。在步进电动机的速度控制过程中,需要按照加速—高恒速—减速—停止的过程进行控制。
可用于步进电动机的速度控制形式通常有指数曲线加减速直线规律与匀加减速直线规律两种。指数曲线作为最理想的加速曲线,虽然可以实现最精准的加速控制,但其实现过程较为复杂,应用较少;而直线加减速曲线具有加速控制较为稳定,编程简单等优点,广泛应用于速度变化较大的快速定位中,因此选取匀加减速直线规律进行智能化步进电动机多轴向的集中控制[9]。
通过对DSP控制系统的软件编程计算,改变脉冲进行步进电动机的速度控制,利用8254定时计数芯片设定时间基准,用f表示DSP的时钟频率,依据连续增减计数模式获取脉冲占空比为50%的PWM脉冲,表示为T1CMPR=T2PR/2。设n为步进电动机运行过程中的速度,N为步进电动机运行的总步数,设置加速步数初始化a=0。速度控制具体实现过程如下:
“起动”:设置n=n低,寄存器周期T=f/2×n,赋值比较寄存器T1CMPR=T2PR/2,智能化步进电动机运动一次时,N--,a++。
“加速”:将剩余步数进行比较[10],可能会存在两种情况:
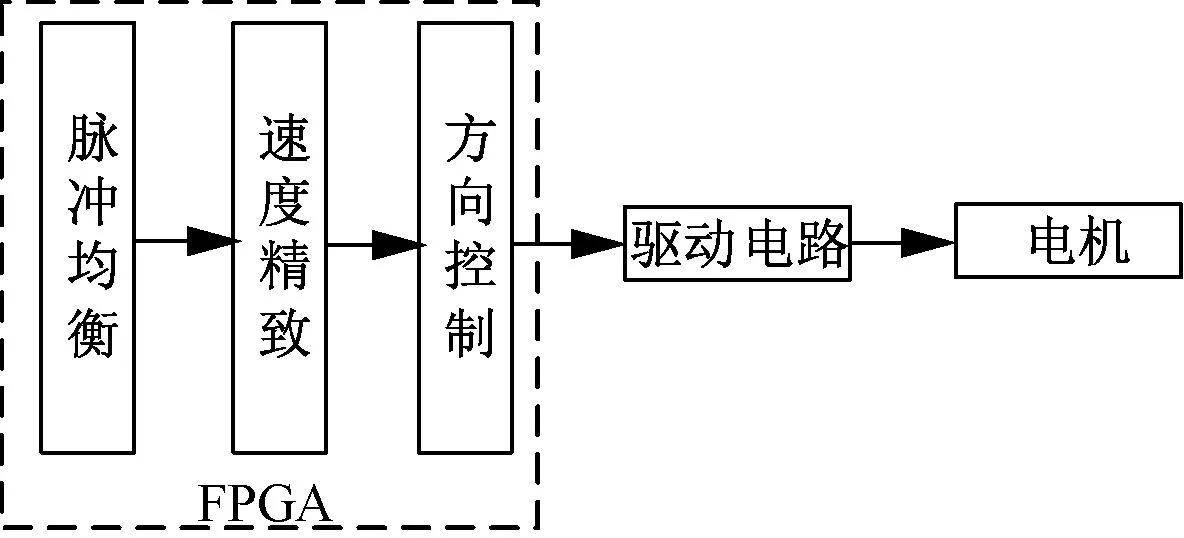
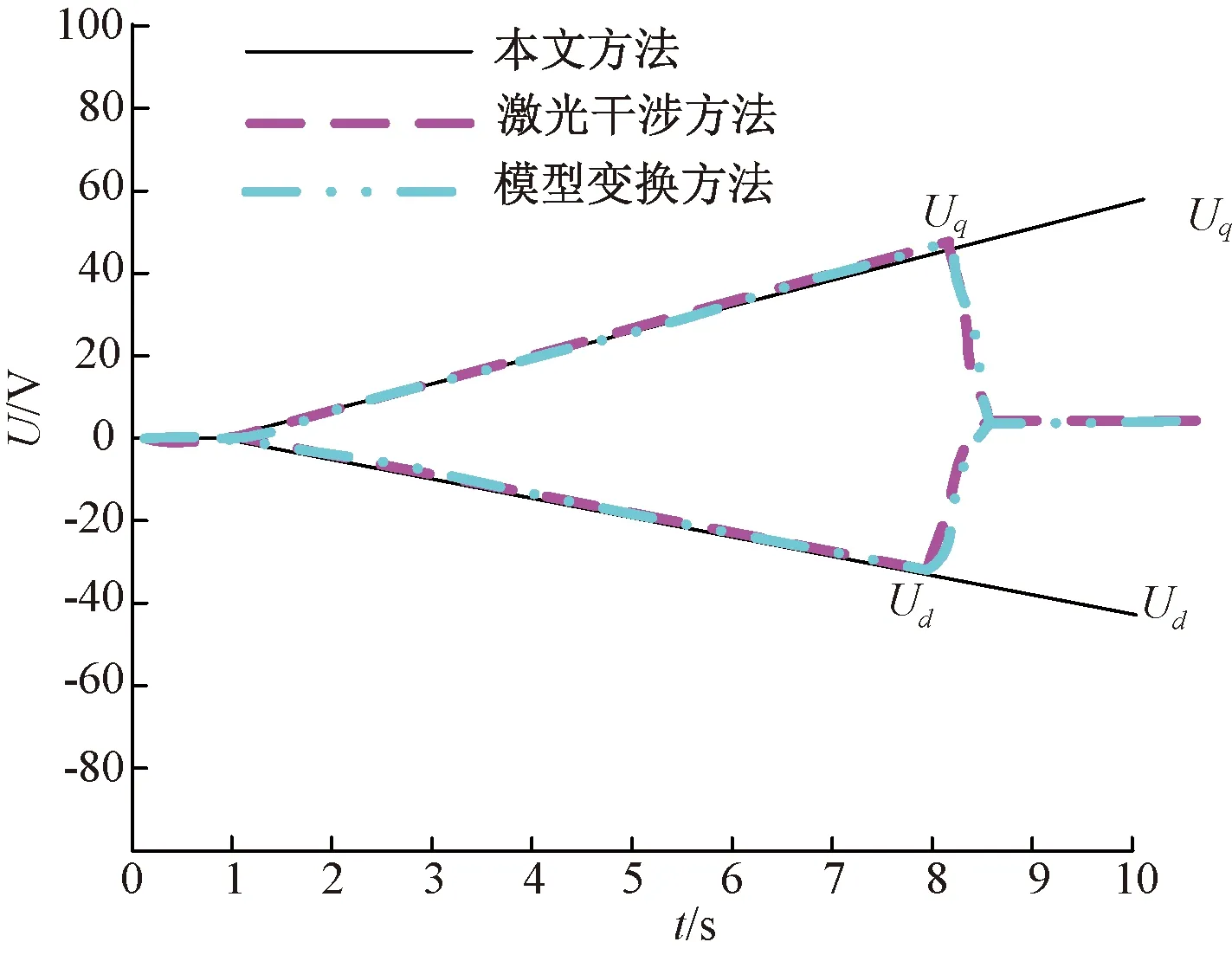
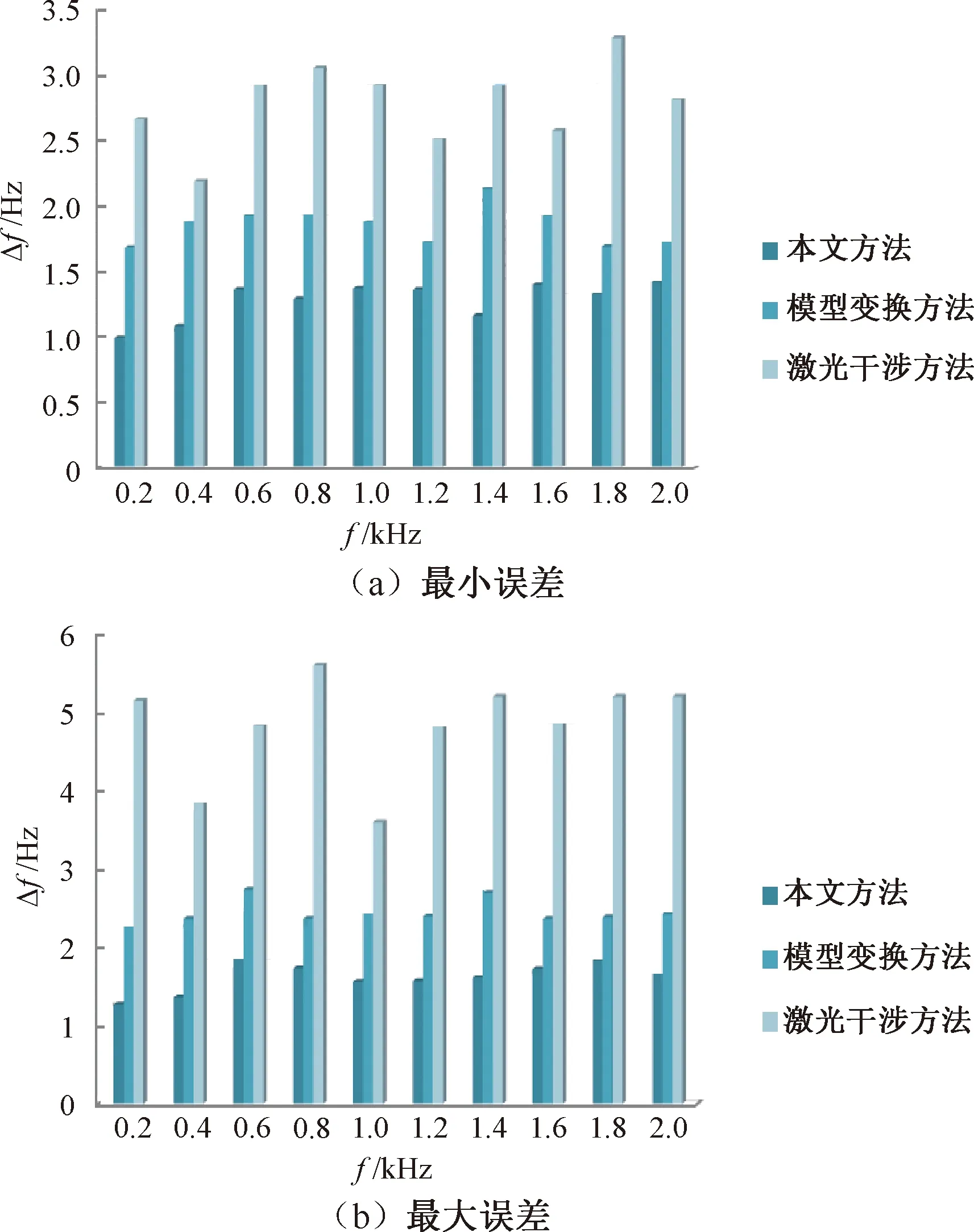
(1)N (2)N>a,发生此种情况时,需要继续进行比较n是否大于n高,若n>n高,表明该轴已完成加速运动,需要进行至“高速”步骤;若n “高速”:设置n=n高,将剩余步数进行比较,若N=a,则步进电动机即将减速,进行至“减速”步骤;否则说明PWM载波频率未有任何变化,则T=f/2×n,比较寄存器T1CMPR=T2PR/2,N--。设置完成后,进行“高速”步骤[11]。 “减速”:当N=0时,说明步进电动机的轴已经完成运动轨迹,此时设置停止运动命令。否则设置下一个脉冲n=n-a/n,设置周期寄存器T=f/2×n,比较寄存器T1CMPR=T2PR/2,N--,执行完成后,继续进行至“减速”步骤[12]。 以上过程中,加速段前后脉冲速度变化Δv如下: Δv=n后-n前 (1) 式中:n前表示加速段前的脉冲速度;n后表示加速段后的脉冲速度。 加速段前后脉冲时间间隔Δt公式如下: (2) 式中:T前表示加速段前的寄存器周期;T后表示加速段后的寄存器周期;f表示标准式中频率;n表示当前步进电动机速度;a表示初始步进电动机速度。 1.3.1 控制方案设计 主要控制功能模块为 FPGA,模块主要包括时钟分频、速度精致和方向控制,这3个部分功能主要是对电机实现控制;利用锁相环 PLL 宏模块,产生 PWM 信号完成速度控制;采用脉冲分配器分成不同步进时序,实现换相控制。具体步骤如图 2 所示。 图2 方案示意图 将两相混合式电机作为研究对象,利用恒流斩波驱动,选用型号42BYG250的电机,以实现正反转功能。该电机具体参数如下:额定电流为0.67 A,额定电压为12 V,步距角1.8°,定位转矩11.8 mN·m,最大空载起动频率在1 000 Hz以上,其运行频率在3 000 Hz以上。 图3 方案硬件结构图 1.3.2 基于均衡脉冲的步进电动机多轴向联动控制模型 多轴向联动的控制接口图如图4所示。通信号(ENABLE)与方向信号(DIR)利用I/O接口IOPBx发送至步进电动机,X轴、Y轴的步进电动机通过GP1的PWM脉冲和GP2的PWM脉冲进行控制。并将DSP与8254定时计数芯片相结合,设置步进电动机神经网络拓扑结构,构建基于均衡脉冲的步进电动机多轴向联动控制模型,从而实现智能化步进电动机的多轴向联动控制。 图4 多轴联动的DSP与步进电动机控制接口框图 步进电动机多轴向控制系统中的DSP需要控制电机,同时要响应外部中断进而调整系统状态以及控制串口发送系统状态数据至人机交互界面,若选取实时计算控制方法,会影响联动控制速度,系统中CPU资源的减少也会影响其他功能的正常运行,因此选取离线计算数据表实时补偿控制方法进行多轴向步进电动机的联动。该方法需要设定其中1个步进电动机中的轴作为时间标准轴,其表达式为: (3) 式中:θ1为步进电动机的转角;d为运动轨迹方程。按照设定的运动轨迹,将运动轨迹以时间标准轴的运动速度为基准分为若干份时间相同的运动轨迹,将获取的小份运动轨迹设置为与运动轴相对应的匀速直线运动[13],利用各项直线运动的调整拟合标准的空间曲线运动,其表达式: (4) 式中:E为运动轨迹的总耗能;I表示联动效果;U表示小份运动轨迹份数。以上过程中,时间相同的小份运动轨迹份数越多,联动效果越好[14]。 在实际联动中,步进电动机神经网络拓扑结构发生变化,由此对神经网络拓扑结构进行联动控制,其优点是网络连通性好、耗能低等。步进电动机神经网络拓扑结构中的全部节点消耗功率之和最低,如果任意节点的半径超过某一阈值,则这个节点能量将会很快消耗,所以超过阈值的半径节点越少越有效。 超过阈值半径Rv的节点数q表达式: CT扫描需要较长的时间,这个过程中,扫描对象如果发生形状、位置的变化,会降低CT成像质量。运动伪影主要分为刚体运动伪影和非刚体运动伪影。 (5) 式中:m为步进电动机神经网络拓扑结构节点数量;i为m个节点中的任意节点,1≤i≤m;Rmax表示步进电动机神经网络节点的最大半径;E为总耗能。 在相同时间内所有轴步进电动机发射的脉冲数δ与电机神经网络拓扑结构,通过轴间的几何运动关系获取,并发送至数据表内,将所有时间的数据累积即可获取所需的数据表[15]。步进电动机轴运动过程中,利用数据表中数据相应的运动时间t,根据均衡脉冲Δδ即可构建相应步进电动机的多轴向联动控制模型,其表达式: minλ= (6) 全部步进电动机在同一时刻起动运动即实现智能化步进电动机的准确多轴向联动。为保证集中控制的准确性,在轴运动过程中可利用DSP实时对智能化步进电动机进行微调,确保各轴向的运动轨迹符合运动要求。 1.3.3 步进电动机多轴向联动流程设计 实施步进电动机的多轴向联动时,依据要求的运动轨迹计算数据表并发送至数据RAM内,在定时计数芯片8254中设定每个步进电动机轴的工作方式。步进电动机起动运动时,将每个步进电动机轴的运动数据发送至该轴的计数芯片8254中,发送数据的同时启动门控信号,电机起动运行。时间标准轴发送第一个脉冲数完成时,同步发送高电平信号至DSP的通用IO口,DSP接收信号后发送全部轴运动的第二份数据至相应定时计数芯片8254开门控信号,步进电动机中各轴接收到信号后发送第二份脉冲数至相应的计数芯片8524中,直至所有运动数据发送完成,运动过程结束。 智能化步进电动机多轴向联动程序流程图如图5所示。DSP在每次完成脉冲发送的同时,需要领取与各轴相对应的8254计数寄存器中的运动数据,若数据领取不够完全,剩余数据则加入下一份数据中以保证步进电动机各轴准确完成运动轨迹。步进电动机脉冲发送速度等于电机轴应发送的脉冲数量与数据运动时间之比,因此若数据运动时间相等,脉冲应基本发送完全,误差较小。在实际电机运动过程中,若出现各轴脉冲发送差别过大的情况,可通过人为中断程序,对轴的运动数据进行调整,保证电机各轴的运动轨迹符合设置要求。利用程序中断调整轴运动数据的时间越短越好,长时间的程序中断会导致系统出现较大的误差。 图5 联动程序流程图 实验对象选取某电网中的步进电动机,型号为57BYG250A,当母线电压是240 V时,智能化步进电动机的最大转速可高达6 000 r/min,设置实验开关频率为5 kHz,给定多轴向电流指令为10 A,步距角为1.8°,步进电动机恒加速运行。图6为智能化步进电动机测试台。 图6 智能步进电动机测试台 根据智能化步进电动机测试台和测试参数,通过计算得到每个脉冲所转过的角度,对智能化步进电动机实测数据进行对比分析。表1为1.8°步距角细分标准值和误差表。 表1 1.8°步距角细分标准值和误差表 由表1可知,在1~128细分的各档位中,每个脉冲所转过角度的绝对误差在5%以内,智能化步进电动机的控制精度较高。通过MATLAB软件仿照实验模块搭建一个仿真平台,为了进一步验证本文方法的性能,将本文方法与激光干涉方法和模型变换方法进行比较,实验测试3种方法进行多轴向集中控制下的步进电动机运行结果,如图7~图9所示。 图7 运行电机转速情况对比 图8 运行电机电流情况对比 图9 运行电机电压情况对比 从图7可以看出,采用本文方法控制的步进电动机运行平稳,在运行9 s时达到最高转速并稳定运行;而采用激光干涉方法和模型变换方法的步进电动机在8 s左右产生旋转偏移,转速降低,导致电机运行异常。由此说明,本文方法可准确控制步进电动机的平稳运行。 从图8可以看出,本文方法控制的步进电动机电流运行过程中维持稳定,并且电流值稳定在给定电流10 A,步进电动机运行电流误差较小;而激光干涉方法和模型变换方法控制的步进电动机运行在8 s时电流出现振荡,步进电动机启动过流保护,停止运行。由此说明,本文方法控制步进电动机电流效果较好,再次验证了本文方法的控制性能。 从图9可以看出,本文方法控制的步进电动机电压随着转速的升高而有所提升,这与实际情况相符;而激光干涉方法和模型变换方法控制的步进电动机电压随着过流保护的停止而返回零值。以上实验结果说明了本文方法具有较好的控制性能。 智能化步进电动机具有矩频特性,最大动态转矩与脉冲频率成反比,为保证步进电动机的出功能力,设置实验智能化步进电动机的工作频率范围为20 Hz~2 000 Hz。为使实验结果更加清晰准确,将实验工作频率范围分成20 Hz~200 Hz、200 Hz~2 000 Hz 2个频率段,利用C++语言编程测量步进电动机脉冲频率精度,并将本文方法与激光干涉方法和模型变换方法进行比较,以给定频率为横坐标,频率误差为纵坐标,频率误差为实际频率与理论频率之差,实验结果如图10、图11所示。 图10 20 Hz~200 Hz频率段电机频率误差 图11 200 Hz~2 000 Hz频率段电机频率误差 从图10和图11可以看出,两种方法的频率误差随着给定频率的增加而增加,本文方法控制的步进电动机误差较小,在给定频率为20~2 000 Hz之间,最大误差均未超过2 Hz,并且输出频率较为稳定,基本无波动。而激光干涉方法和模型变换方法控制的步进电动机误差较大,波动范围大,输出频率不稳定。 为进一步分析两种方法对步进电动机的控制稳定性,在3个频率段内分别选取100 Hz、500 Hz和1 000 Hz 3个频率值进行10次测试,测试结果如表2所示。 从表2输出频率结果对比可以看出,本文方法控制的步进电动机在给定100 Hz、500 Hz和1 000 Hz 3个频率值时的输出频率误差均不超过2 Hz,明显低于激光干涉方法和模型变化方法控制的步进电动机输出频率误差,说明了本文方法控制的步进电动机具有较高的精准性。 统计上述步进电动机控制实验过程中,两种方法的控制性能,统计结果如图12所示。 图12 3种方法控制性能对比 从图12可以看出,本文方法的控制精度、控制效率、鲁棒性以及灵敏性均高于95%,耗能性数值低于5%,各项性能均优于激光干涉方法和模型变换方法。对比结果说明本文方法对步进电动机具有较高的控制性能,应用价值高。 对两种传统方法和本文方法的应用过程同时施加相同的外界干扰,对比统计不同方法的电压波动值,比较结果如图13所示。从图13可知,传统步进电动机多轴向联动控制方法的电压波动较大,大概分布在-40~40 V之间。本文方法的电压波动值稳定在-10~10 V之间。可以看出,本文方法受到外界干扰时电压波动值明显低于传统模型,表明本文模型的抗干扰能力明显较强。 图13 模型抗干扰能力测试比较结果 随着工业生产步入智能化,对步进电动机的精度要求越来越高,本文研究了智能化步进电动机的多轴向控制方法,通过步进电动机多轴向的联动实现智能化步进电动机的高效控制。实验结果表明,该方法进行多轴向集中控制下的步进电动机控制精度高,运行过程稳定,并且多轴向集中控制精度、控制效率、鲁棒性以及灵敏性均高于95%,耗能性数值低于5%,具有理想的抗干扰性能,是一种高效环保的步进电动机多轴向集中控制方法,可应用于实际的工业生产中。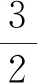

1.3 步进电动机多轴向联动控制



2 实验分析







3 结 语
