极弧系数对永磁同步电机齿槽转矩影响的分析
2022-08-25钟成堡陈飞龙杨文德
刘 娜,钟成堡,2,陈飞龙,2,杨文德,2
(1.珠海格力电器股份有限公司,珠海 519000; 2.广东省高性能伺服系统企业重点实验室,珠海 519070)
0 引 言
随着电机及其控制技术的发展,市场对电机的输出性能要求越来越高。特别是高精度应用场合,对电机的定位精度、转速波动和转矩脉动等提出越来越高的要求。
齿槽转矩对永磁同步电机的定位精度和转矩脉动等性能有很大的影响。为了消除或削弱齿槽转矩,国内外众多专家学者和工程技术人员都做了许多相关的研究和实验。文献[1]采用不等极弧系数组合的方法来削弱永磁直流电机的齿槽转矩,利用基于能量法和傅里叶分解的解析法得到齿槽转矩的表达式,通过分析起作用的气隙磁密的傅里叶系数,给出了使得齿槽转矩最小的极弧系数组合的确定方法。文献[2]通过分析采用不同分段磁极结构时的齿槽转矩解析表达式,给出了最佳极弧系数组合和倾斜角度的确定方法,最终验证了该方法降低齿槽转矩的可行性。文献[3]提出一种在电机转子轴向组合不同永磁体的方法来减小电机齿槽转矩。采用能量法和傅里叶分解法分析了齿槽转矩,并基于该方法计算出组合永磁体具体尺寸的方法,最后利用有限元法检验了该方法的有效性。文献[4]提出采用分块磁极等宽极厚正弦调制的方法优化永磁同步电机气隙磁密和齿槽转矩。有限元仿真分析验证了该方法的正确性,表明该方法能有效抑制永磁同步电机气隙磁密谐波分量,在一定极弧系数范围内对齿槽转矩抑制具有较好的效果。文献[5]利用有限元方法分析了极弧系数变化、磁极移动和开辅助槽对永磁电机齿槽转矩的影响, 实验表明根据电机具体的参数选择合适的方法可以有效地减小齿槽转矩。文献[6]运用齿槽转矩叠加原理,把定子铁心的槽分组,每组槽偏移一定角度,计算出了最优槽口偏移角,并采用有限元软件验证了该方法的可行性。
以上文献主要从不同分段磁极优化、永磁体形状优化等方面分析了极弧系数并最终削弱齿槽转矩。本文提出了通过设计电机极弧系数大小来优化电机齿槽转矩的方法,首先从齿槽转矩表达式分析了极弧系数是影响齿槽转矩的关键因素,理论分析出对于固定极槽配合的电机,存在固定的极弧系数使电机齿槽转矩为零或近似为零。用有限元软件Maxwell建立了二维电机模型,通过仿真不同转子外圆形状和不同磁钢厚度下电机的极弧系数和齿槽转矩,得出极弧系数是影响电机齿槽转矩的关键因素,当极弧系数等于或接近0.6或0.8时,12槽10极电机齿槽转矩最小。
1 极弧系数对齿槽转矩影响的理论分析
根据齿槽转矩定义及能量法理论可得:
(1)
式中:Tcog代表齿槽转矩;W代表磁场能量;α代表定子与转子的相对位置角。
假设电机定子和转子铁心使用硅钢片的磁导率为无穷大,则齿槽转矩表达式:
(2)
式中:z代表定子槽数;p代表极对数;LFe代表电枢铁心长度;R1代表定子内半径;R2代表转子外半径。
由理论分析可知,除了定子槽数、定转子尺寸等因素,永磁体剩磁Br是影响齿槽转矩的关键因素,但不是所有阶次的Br都对齿槽转矩有影响,只有nz/2p阶次剩磁产生齿槽转矩。本文电机为12槽10极,则齿槽转矩只与5k(k为正整数)阶次的剩磁有关。不同阶次剩磁计算公式如下:
(3)
式中:αp代表极弧系数。
从式(3)可知,极弧系数是影响剩磁的关键因素,只要能使nαp为整数,则n阶次的剩磁产生的齿槽转矩为0。由于本文电机有效阶次n=5k(k为正整数),所以能使nαp为整数的最佳极弧系数理论计算典型值为0.6和0.8。
2 极弧系数解析分析
电机极弧系数等于气隙磁密平均值与气隙磁密最大值之比。其计算公式如下:
(4)
式中:Bδav代表气隙磁密平均值;Bδmax代表气隙磁密最大值。
综合以上分析,气隙磁密的分布形式和大小是影响电机齿槽转矩的关键因素。
3 极弧系数对齿槽转矩影响的有限元分析
3.1 样机模型主要参数
本文以12槽10极磁钢切向嵌入式永磁同步电机为例进行仿真分析,主要参数如表1所示。
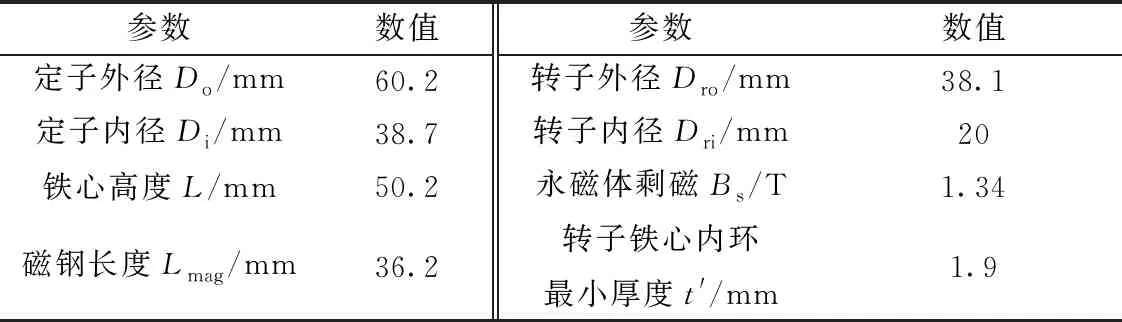
表1 样机主要参数
根据样机参数建立电机二维模型如图1所示。
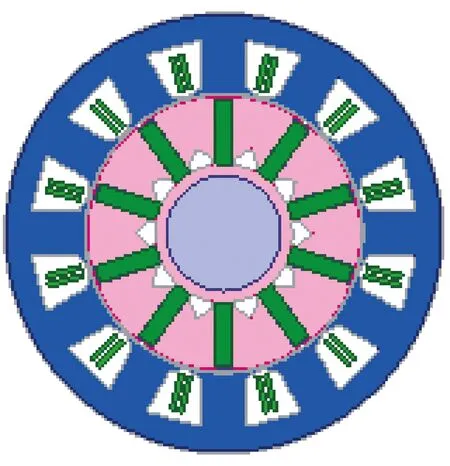
图1 样机二维模型
本文电机转子外圆轮廓由10个相同单元构成,如图2和图3所示。每个单元分别由直线段1、直线段2和中间圆弧段构成,直线段1与直线段2关于圆弧段中心对称。两直线段夹角定义为Ф,圆弧段的圆心与转子中心的距离定义为偏心距O,磁钢厚度定义为t,磁钢长度定义为Lmag,转子铁心内径与磁钢间最小铁心厚度定义为t',转子外圆隔磁桥最小厚度(两个直线段交点与磁钢最小距离)定义t″,极间弧长(极距)定义为τ。
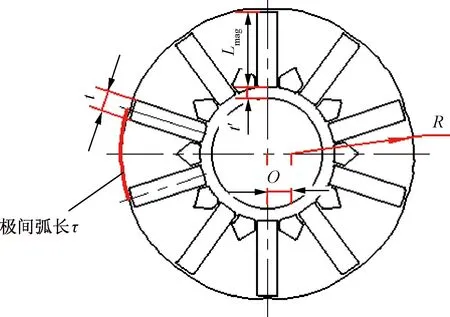
图2 转子形状及参数示意
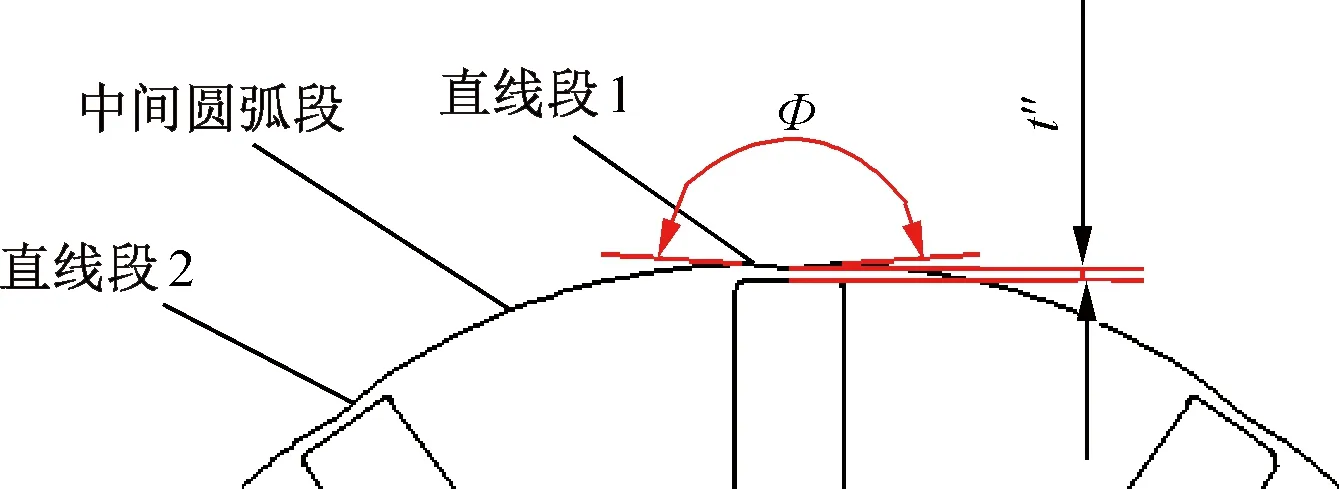
图3 转子局部放大图
3.2 齿槽转矩有限元仿真方法分析
建立好模型后,模型属性定义为瞬态场。转速设置500 r/min,本文电机槽极配合方案为12槽10极。由理论分析可知,齿槽转矩周期为2 ms。齿槽转矩仿真曲线示意图如图4所示。
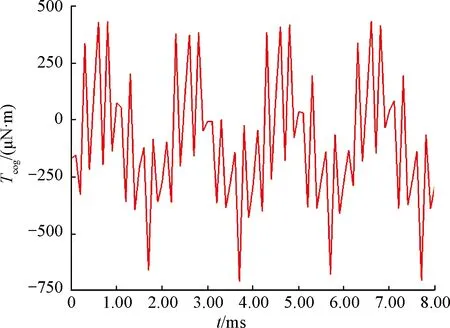
图4 电机齿槽转矩仿真曲线
3.3 极弧系数有限元仿真方法分析
建立好模型后,模型属性定义为静态场。提取转子外圆与定子内圆的中心圆圆周磁密曲线,根据上述理论分析,计算该曲线平均值与最大值之比即为电机极弧系数。
计算极弧系数的中心圆圆周磁密仿真曲线示意图如图5所示。
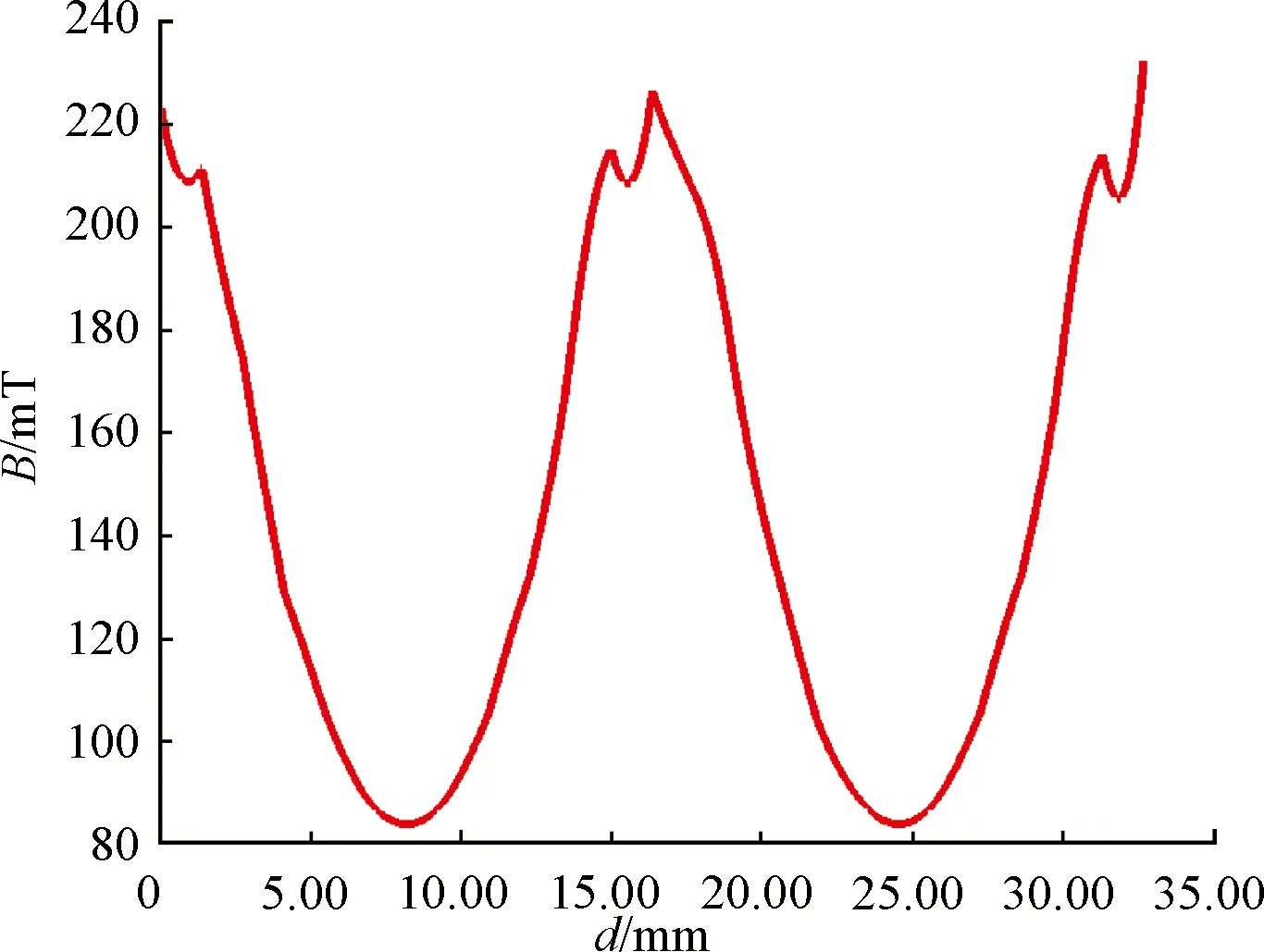
图5 转子外圆与定子内圆的中心圆圆周磁密示意图
3.4 转子外圆形状对电机极弧系数和齿槽转矩的影响
转子外圆形状由前面提出的电机参数决定,设计惯量决定了转子外圆和铁心高度。由于转子铁心与轴间为过盈配合,且该过盈力需要足够大来抵抗电机切向电磁力和转子离心力,所以转子铁心内径与磁钢槽间最小厚度t'由结构强度决定。转子外圆隔磁桥最小厚度t″越小,隔磁效果越好,t″由铁心模具制作工艺能够达到的最小值决定。本文在Lmag为固定值的情况下,仿真分析两段直线夹角Ф和偏心距O不同组合对电机极弧系数和齿槽转矩的影响规律,最终分析出12槽10极电机极弧系数对齿槽转矩的影响。
(1)转子外圆形状对电机极弧系数的影响
仿真分析不同Ф和O组合时电机极弧系数的大小,仿真结果如表2所示。
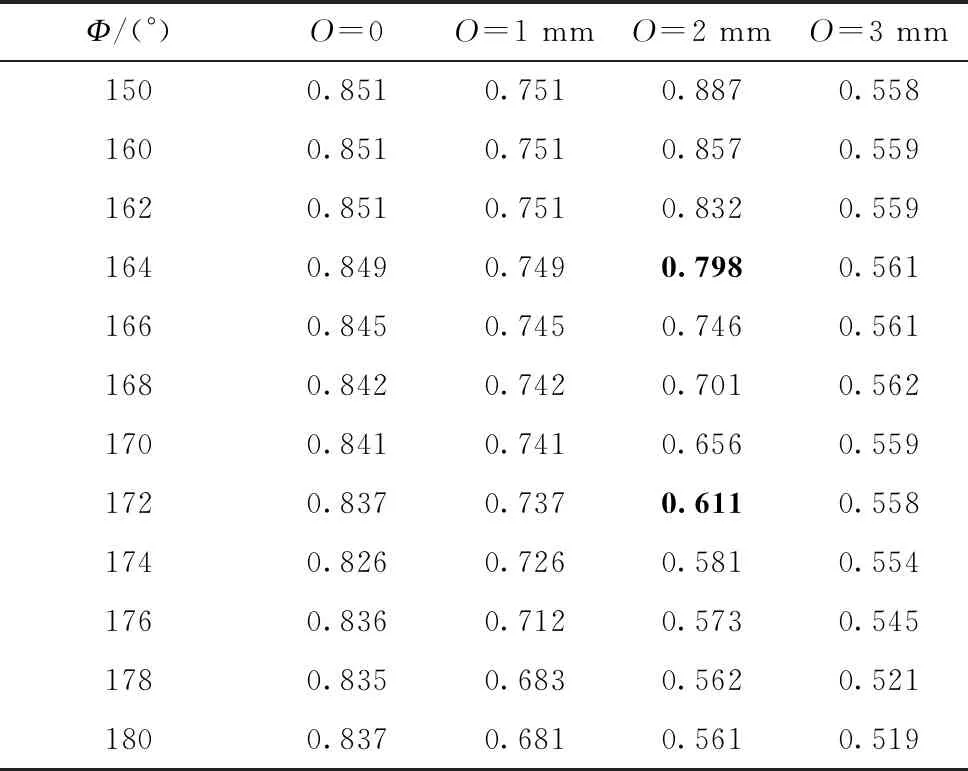
表2 不同Ф和O组合时电机极弧系数仿真值
从表2可以看出,转子外圆形状是影响电机极弧系数的关键因素。电机极弧系数随着转子外圆弧偏心距的增大而逐渐减小,同时极弧系数随着角度Ф的增大而逐渐减小。
从极弧系数对齿槽转矩的影响理论分析可知,对于12槽10极电机,当极弧系数为0.6或0.8时,电机齿槽转矩为最小。
从表2可以看出,当O=2 mm且Φ=172°时,电机极弧系数近似等于0.6;当O=2 mm且Φ=164°时电机极弧系数近似等于0.8。
(2)转子外圆形状对电机齿槽转矩的影响
仿真分析不同Ф和O组合时电机齿槽转矩的大小,仿真结果如图6所示。

图6 不同Ф和O组合时电机齿槽转矩仿真值
从图6可以看出,当O=2 mm且Φ=172°时,电机齿槽转矩为3.1 mN·m;当O=2 mm且Φ=164°时,电机齿槽转矩为3.2 mN·m。此两种情况下电机齿槽转矩最小。
从以上仿真可以看出,电机齿槽转矩最小时电机极弧系数分别近似等于0.6和0.8。此结论与理论分析结果一致。
3.5 磁钢厚度与极距比对电机极弧系数和齿槽转矩的影响
磁钢厚度不同,磁力线的磁路走向就不同,如图7和图8所示。磁钢厚度越小,转子的有效极弧长度越大;磁钢厚度越大,磁力线越向磁极中心聚拢,有效极弧长度越小。

图7 磁钢厚度小时磁力线走向
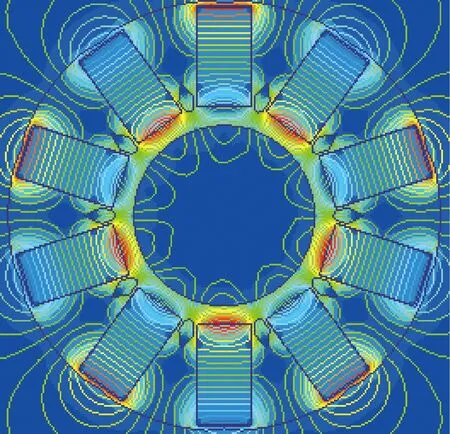
图8 磁钢厚度大时磁力线走向
仿真不同t/τ时电机的齿槽转矩,结果如图9所示。
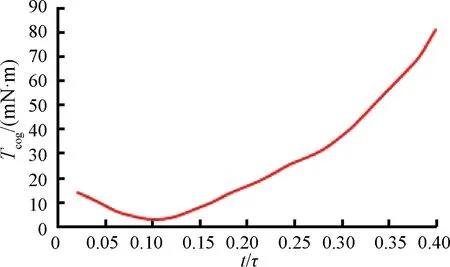
图9 齿槽转矩随t/τ变化曲线
由仿真结果可以看出,齿槽转矩随着t/τ的增大,先减小后增大。当t/τ=0.11时电机齿槽转矩最小,仿真此种情况下的转子外圆与定子内圆的中心圆圆周磁密,曲线如图10所示。通过该曲线计算的电机极弧系数等于0.62,与理论分析最佳极弧系数0.6基本一致。
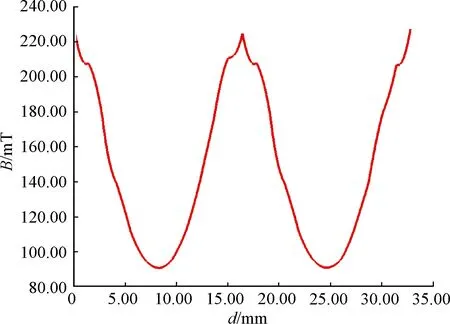
图10 t/τ=0.11时转子外圆与定子内圆的中心圆圆周磁密
4 齿槽转矩实验测试与结果分析
将电机安装在齿槽转矩测试台上,采用扭矩传感器对电机齿槽转矩进行测试,得到结果如图11所示。
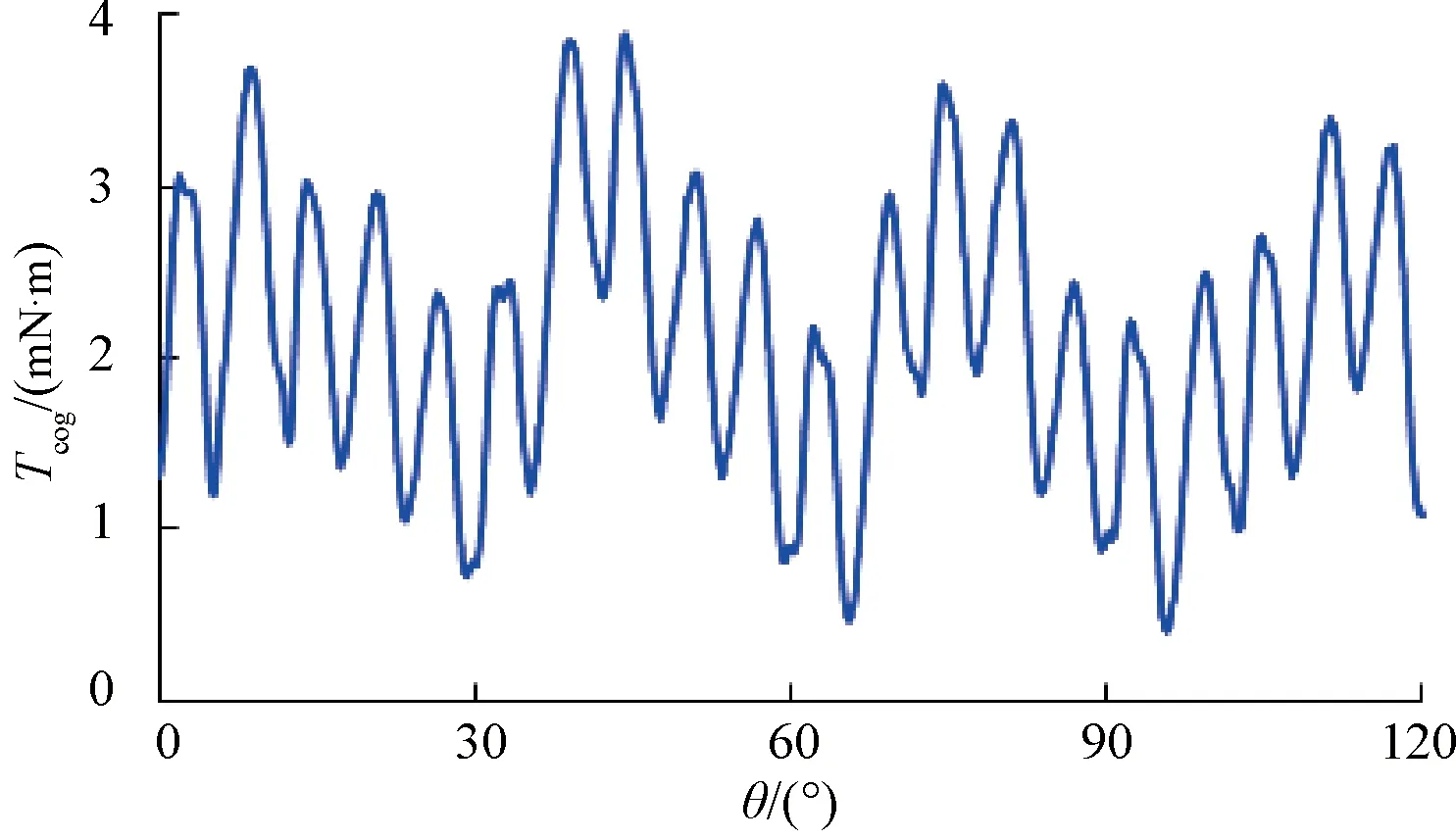
图11 齿槽转矩测试曲线
实测齿槽转矩为3.3 mN·m,与仿真最优方案齿槽转矩相差5.7%,满足设计要求。
5 结 语
本文提出了通过设计电机极弧系数来优化电机齿槽转矩的方法。通过推导电机齿槽转矩解析式得出,对于固定极槽配合的电机,存在固定的极弧系数使电机齿槽转矩为零或近似为零。用有限元软件Maxwell建立了二维电机模型,通过仿真不同转子外圆形状和不同磁钢厚度下电机的极弧系数和齿槽转矩,得出极弧系数是影响电机齿槽转矩的关键因素,对于12槽10极电机,当极弧系数等于或接近0.6或0.8时,电机齿槽转矩最小。最后通过电机齿槽转矩测试验证了本文方法的正确性。该方法对于指导实际产品设计具有较大参考价值。
