军用循环包装箱金属卡扣的寿命分析与仿真

杜雨芳，游藩，徐炜峰，刘卉＊，高静

（1. 中国包装科研测试中心，天津 300385；2. 中国人民解放军32382部队，北京 430311）

根据航空、军用装备器材的性能和使用方式，部分装备器材交付使用后，在使用、仓储等期间，对部分贵重部件、器材按照规定途经和要求对航空器材、军用装备等送修返修[1]，在此情形下，航空、军用装备器材等在其寿命期内，可能需要多次搬运、转运、仓储、使用，其配套包装也应满足多次循环使用的需求。为确保装备、器材等在运输、转运、仓储过程中的安全与可靠性，评估配套循环包装的可靠性是重要的保障工作。循环包装的可靠性涉及一整套包装系统的可靠性，本文从某循环包装箱的金属部件着手，评估金属部件寿命是否能满足循环包装箱的可靠性需求。

本文以某军用器材循环包装箱的金属部件——卡扣为研究对象，分析卡扣在安装、拆卸过程及工作状态下的工作原理，对卡扣进行应力分析，计算寿命，同时利用有限元分析软件ANSYS Workbench模拟卡扣的装卸过程，得到卡扣的寿命，以评估是否满足循环使用需求及循环使用中的可靠性。

1 循环包装箱金属部件工作原理介绍

某军用战备器材某型包装箱（图1）为配合战备转运等需求，包装箱要完成反复拆装50次以上，即金属件卡扣需满足循环使用至少100次，箱体主要由四个侧面、底座、顶盖六部分构成，包装箱正常使用状态下四个侧面、顶盖之间由卡扣（图2）连接固定。为确保包装箱循环使用中的可靠性，对该型号包装箱用量最多的金属部件——卡扣进行可靠性评估，计算卡扣的使用寿命。

图1 循环包装箱

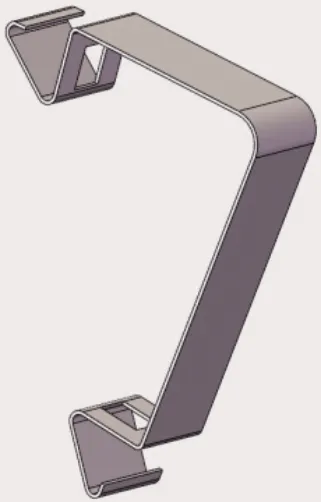
图2 卡扣

该包装箱卡扣在未安装时约为85°角，采用65Mn弹簧钢加工而成，在卡扣寿命期内要满足反复拆装100次以上不发生永久变形，且使用过程中卡扣无裂纹产生。卡扣的工作原理如下：

安装时先卡紧短边，再按压长边以卡在底座上固定，工作状态下保持90°，卡扣两侧张紧；拆卸时由外力翘起长边，卸离底座（图3）。因底座固定于箱体上，在包装箱循环使用中不存在反复拆卸情况，本文仅考虑卡扣的疲劳情况与寿命。

图3 卡扣安装拆卸与工作示意图

2 卡扣载荷分析与计算

卡扣在安装或拆卸中受到足够大的力才能实现安装或拆卸，实测安装拆卸过程需要50-75N，考虑实际操作中拆卸的一些不确定因素，拆卸力考虑冗余量，拆卸力为150N，在正常工作中卡在两个梁边缘，呈张紧状态，受力约为40-50N。工作状态下卡扣的三个角（图4）α1=α2=α3=90°，在工作条件下，拐点应力由两部分产生：弯矩和剪切力（或正向拉力）。

图4 卡扣工作状态受力示意图

卡扣在反复安装、拆卸、卡紧状态下，卡扣拐点c是主要关注点，无论何种工作状态，该点都是主要受力点，按照疲劳寿命计算基本法[2]中局部应力——应变法，若一个构件危险区的应力——应变历程与一个光滑试件的应力——应变历程相同，则寿命相同[3]，卡扣整体疲劳情况以该点做参考。卡扣拐点c处应力σ由弯矩与正向拉力产生，保守估计为两者之和，σ=σb+σs，卡扣横截面为矩形面，惯性矩为I=bh3/12，剪切力或正向力的应力=F/A，b点弯矩Mb=Fl+Ma，c点弯矩Mc=Fl+Mb，经计算，卡扣工作状态下的应力：

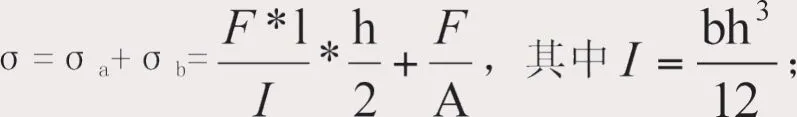
代入卡扣相关数值，得到应力σ=136Mpa。

在该模型中，安装、拆卸过程相似，安装完毕瞬间与拆卸开始瞬间过程受力状态基本一致，卡扣在安装或拆卸中的中间受力情况，以安装或拆卸即将呈现工作状态的瞬间受力最大，因此以工作状态相似的瞬间计算，得到表1中卡扣在安装、拆卸、工作中的受力和应力值。卡扣在寿命周期内反复拆装，出现裂纹或永久变形则到达寿命极限，整个过程建立疲劳模型，考虑卡扣表面处理、表面质量、尺寸效应等因素，根据《应力集中系数手册》等资料选择应力集中系数Kt=2.2，疲劳因子f=1.21，得到疲劳因素影响下的应力值[σ]=σ＊f＊Kt，并绘制工作中的应力谱（图5）。

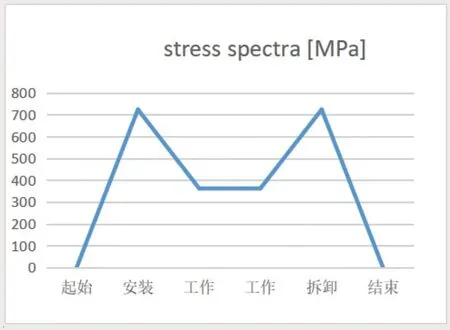
图5 卡扣工作应力谱

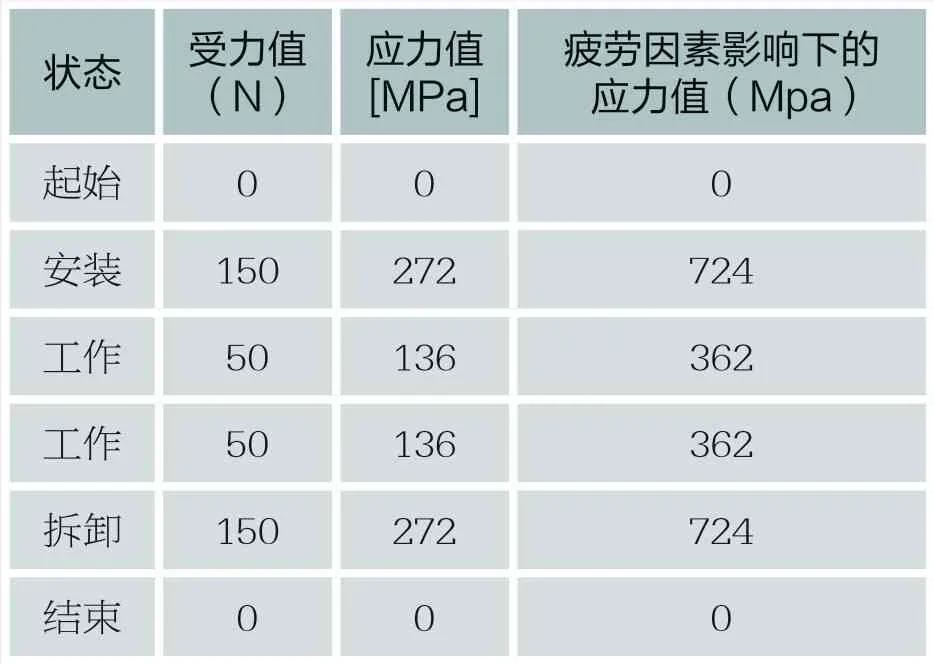
表1 卡扣应力值

3 疲劳寿命与损伤分析

卡扣重复安装、拆卸、工作的过程载荷循环往复，根据卡扣工作应力图谱归结该模型为低周疲劳损伤模型，该过程载荷应力能够引起卡扣材料力学性能劣变，产生疲劳累积损伤，根据Palmgren-Miner线性积累损伤准则[4]，卡扣疲劳损伤D为使用应力下的循环次数n与该应力下材料疲劳寿命N的比，公式为：

卡扣设计寿命n=100次，根据卡扣材料的S-N曲线（图6），疲劳因素下的应力值为724Mpa，log（7.24＊108）=8.9，对应logN=2.6的疲劳寿命N=398次，D=n/N=0.25，考虑疲劳中散射因素，D=n/N＊2=0.5，D＜1，符合低周疲劳损伤理论。因此理论计算卡扣的使用寿命为398次。

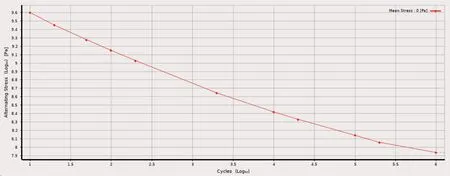
图6 结构钢的S-N曲线

4 卡扣疲劳仿真模拟

卡扣的工作状态按准静态分析，由图5卡扣应力谱可得知，在卡扣安装或者拆卸时受应力最大，结合实际使用情况，在安装和拆卸情况下最容易发生疲劳或者永久变形，因此在有限元仿真时主要考虑该工况下的疲劳，以安装或拆卸瞬间最大力情况加载载荷，以模拟卡扣的疲劳工况。

将已有的卡扣数模导入到ANSYS Workbench软件中，建立Static Structure模型。卡扣材料为65Mn弹簧钢，表2是相关材料参数，导入到材料库中，并在Model中赋予卡扣材料属性。

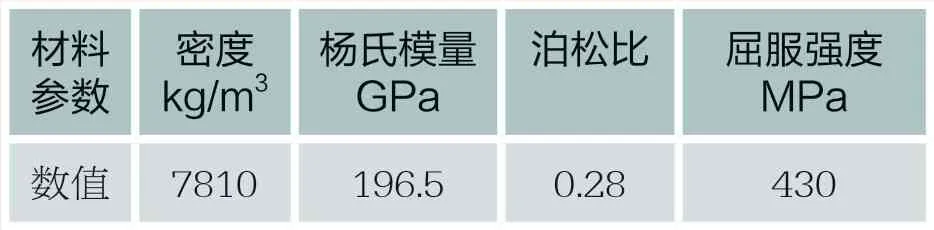
表2 材料参数

卡扣结构特点为长宽方向远大于厚度方向，在模拟卡扣时，将卡扣作为壳单元处理，因此在对卡扣进行网格划分时，首先进行抽中面处理，然后赋予卡扣实际厚度1.5mm的数值，再对卡扣的壳做网格划分，网格以四边形为主（图7），网格质量中等。

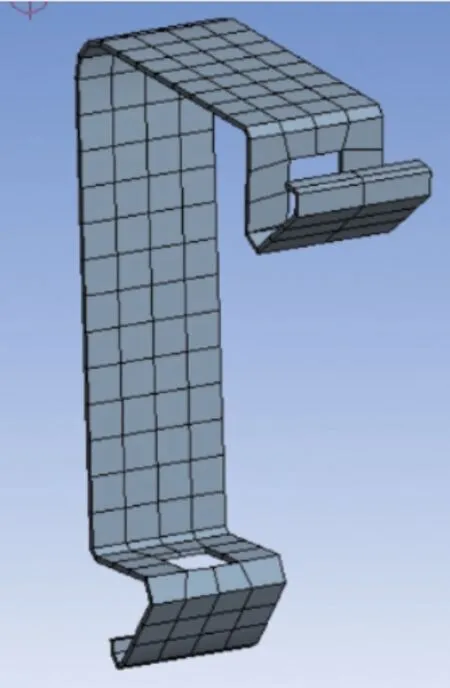
图7 卡扣网格划分

按照前文对卡扣工作情况的分析，卡扣在安装或拆卸时受力最大，瞬间工况为长边一侧受力，因此为卡扣长边边缘添加载荷，以最严酷状态下即载荷最大150N加载集中力；然后再为卡扣添加约束，以短边一侧固定添加固定约束，完成卡扣模型前处理，并进行solve运算。

运行模型结束后，在Solution中添加应力、应变，以及fatigue tool。再次运行后得到应力、应变、寿命云图（图8），拐点附近卡扣有应力集中发生，且拐点处应变最大，该处容易发生疲劳损伤，与力学分析基本一致。根据云图，所受的最大应力为837Mpa，应变最大处及损伤易发生处，寿命为377次。

图8 卡扣应力、应变、寿命云图

受力分析计算得到卡扣所受的最大应力为724Mpa，与仿真模拟结果的应力值837Mpa接近，约15%的误差，寿命数值接近，仿真结果趋势与分析一致。

5 结论

本文经过对卡扣安装、拆卸、工作状态下应力情况分析，应用低周疲劳模型对卡扣的使用寿命进行计算，得到卡扣的使用寿命为398次；同时对卡扣进行有限元仿真计算，模拟卡扣准静态下安装或拆卸工况，得到卡扣的应力、应变以及疲劳寿命377次。结合计算与仿真分析比对，两者应力与寿命接近，得到卡扣的疲劳可靠性可以满足使用需求。

因此，循环包装箱的金属部件——卡扣在安装、拆卸和工作状态下，疲劳强度满足使用要求，使用寿命300次以上，能够满足可循环包装箱循环拆卸50次，卡扣反复拆卸100次的使用要求，金属部件的可靠性能够达到包装箱系统循环使用要求的可靠性。