波纹板结构参数对传热及力学特性的数值研究

苏厚德 徐建新 张玉福 马一鸣 张型波 武建军

（1.甘肃蓝科石化高新装备股份有限公司；2.兰州大学 西部灾害与环境力学教育部重点实验室 土木工程与力学学院；3.上海蓝滨石化设备有限责任公司）

板式换热器是一种热能传递装置，广泛应用于石油、化工等相关领域。 目前对其传热与压降特性的研究主要基于实验或模拟。 在实验研究方面， Focke W W等通过实验得出了流体在波纹板间流道的流动形式随波纹倾角的变化规律，当波纹倾角小于60°时，流动形式为“十字交叉流”；波纹倾角大于60°时，流动形式为“曲折流”［1］。 Hessami M A通过实验得出波纹倾角为60°时的努塞尔数是45°时的1.5～2.0 倍［2］。 Khan T S等对30°/30°、60°/60°和30°/60°不同组合的波纹倾角的人字形波纹板， 进行了单相流在雷诺数500＜Re＜2500和普朗特数3.5＜Pr＜6.5的范围内变化的实验研究，得出了波纹倾角和雷诺数对板式换热器的传热特性有重要的影响［3］。 Muley A和Manglik R M通过实验研究波纹夹角与面积扩展系数的影响，并在此基础上推出传热准则关系和摩擦系数的表达式［4］。 Kumar B等通过实验研究表明了矩形波纹板片的波纹倾角对板式换热器的水力和热工性能有明显的影响作用， 且波纹倾角越大，流体沿流道方向的阻力损失越大［5］。Gherasim I等对波纹流道的平均努塞尔数Nu和摩擦阻力系数f随波纹倾角的变化规律进行了实验研究得出，流道的平均Nu和f随 的增大而增大， 并对波纹板面上局部Nu的测定发现，在波纹板的迎风面上局部Nu数较大，而波纹板的背风面和波纹沟槽底部的Nu较小［6～8］。

实验研究虽能满足换热的实际工况，但成本高、周期长，人们逐渐开展了一些数值研究。 最初，数值模拟板式换热器模型为单流道［9～14］，主要研究波纹板的结构参数对流动形式、传热和阻力的影响。 但对于板式换热器，单流道的数值模拟可以得到几何参数对人字形板式换热器内流动形式、传热和阻力的影响，但不符合实际的换热工况。 因此，对于双流道耦合传热模拟研究是非常有必要的。 张玉宝以双流道耦合传热模型为研究对象，模拟得到换热器的传热特性和压降及阻力特性与波纹板结构参数有关［15］。 徐志明等通过建立双流道耦合传热模型， 拟合出了传热关联式，并运用传热量与功率的消耗比来评价板式换热器的综合性能［16］。 邱小亮利用实验和数值模拟两种方式，分析了两流体在相同速度和变速两种情况下传热与流阻特性，并提出混合流动形式比单纯的十字交叉流或曲折流的换热效果要好［17］。牛骁建立了一种非对称板式换热器的模型，模拟研究了高低波纹高度之比对非对称板式换热器的传热性能的影响， 提出了用不对称度N为衡量高低波纹高度差的指标，拟合出了关于不对称度N的努塞尔数和摩擦阻力系数的关联式［18］。可见，以上研究主要考虑如何提高换热效率，减低压降方面，但并未考虑波纹板结构参数的变化对板片受力情况的影响。

笔者建立人字形双流道耦合传热物理模型，通过改变换热器的波纹倾角β、波纹间距λ和波纹高度H，分析其对传热及流阻性能的影响规律，并考虑波纹板片在流体不均匀载荷下的承载能力，将流体流动产生的压力载荷结果导入Static Structural模块，对板片进行流-固耦合计算，得到不同板片结构参数在不同工况下的最大变形和最大等效应力的变化规律。

1 基本模型

1.1 物理模型

为研究波纹板换热器的结构参数对传热和力学特性的影响， 建立如图1所示的冷热双流道模型，冷热流体逆向流动，上侧流道流动热流体，左侧流入，右侧流出；下侧流道流动冷流体，右侧流入，左侧流出。

图1 冷热双流道几何模型

1.2 数学模型

1.2.1 流体控制方程

因传热过程为水-水间换热，没有相变，且内温差小，故可假设：

a. 流体在换热器中处于稳定流动和换热状态；

b. 流体介质流动的粘性耗散作用下产生的热效应可忽略；

c. 换热器与周围环境绝热；

d. 流道内均匀充满介质。

在以上假设的基础上， 流体控制方程包含有：

中间壁面：耦合壁面，即两流道中的流体通过中间换热板进行耦合换热。

1.2.4 网格划分与离散求解方案

由于波纹板间为复杂的三维流道，采用非结构四面体网格划分算法，并对局部进行加密网格处理，网格大小为0.6 mm（网格数约为350万）时，划分效果如图2所示。

图2 模型网格划分效果

湍流模型采用RNG k-ε 模型，以SIMPLE算法耦合速度与压力；壁面使用增强壁面函数（Enhanced Wall）。 扩散项采用中心差分格式；动量、湍动能和湍动能耗散率的对流项采用二阶迎风格式。

2 模拟算法的合理性验证

为验证上述算法在人字形波纹板换热器的模拟中的合理性，对换热实验系统［19］中的人字形波纹板进行数值模拟，其结构参数：

通过模拟不同入口流速u0（0.2～1.0 m/s）时，得到该换热器的摩擦阻力系数f和努塞尔数Nu在不同雷诺数Re下的变化规律与文献［19］的实验结果对比，如图3所示。

图3 换热器的传热与流阻性能的模拟值与实验值对比

由图3可见， 模拟得到的努塞尔数Nu和摩擦阻力系数f在不同雷诺数Re下的变化规律与实验得到的相同——随着雷诺数Re的增大努塞尔数Nu逐渐增大、摩擦阻力系数f缓慢减小。通过对比，数值模拟结果与文献［19］的实验结果的最大误差小于10%， 表明本理论模型及其求解方法的正确合理、计算结果可靠。

3 波纹板的结构参数对传热与流阻性能的影响分析

3.1 波纹倾角

对于给定波纹间距λ=11 mm、波纹高度H=3 mm的波纹板，在不同波纹倾角β时，努塞尔数Nu随雷诺数Re的变化规律和摩擦阻力系数f随雷诺数Re的变化规律由图4所示。

由图4a可见：当波纹倾角β相同时，波纹板的努塞尔数Nu随着流体雷诺数Re的增大而增大且近似呈线性关系， 这是由于随着流体的流速增大，导致其湍动能不断增大，继而强化了传热；当流体雷诺数Re不变时，努塞尔数Nu随着波纹倾角β的增大是先增大后减小， 这是由于流体在流道的流动形式随着波纹倾角的增大发生转变，在波纹倾角65°附近时，出现混合流动，致使努塞尔数Nu达到最大，此时传热效果最好。

由图4b可见，流体雷诺数Re不变时，摩擦阻力系数f随着波纹倾角β的增大先增大后减小。 这是由于随着波纹倾角不断增大，波纹板间的接触面数目不断减少，流体沿波纹方向的动量分量先增大后减小， 致使流动阻力也是先增大后减小，在波纹倾角65°附近时，流动阻力达到了最大值。

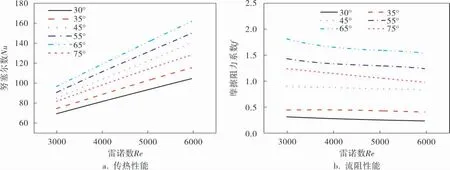
图4 不同β下换热器的传热与流阻性能的模拟值与实验值对比

为方便衡量，引用“面积质量因子”，即换热因子j=Nu/（Re·Pr1/3）与摩擦阻力系数f的比值j/f来表示人字形板式换热器的综合换热性能：面积质量因子越大，表明综合换热性能越好。 不同波纹倾角β下的面积质量因子j/f随雷诺数Re的变化规律如图5所示。

图5 不同β下的j/f随Re的变化规律

由图5可见：β＜65°时面积质量因子j/f随着波纹倾角β的增大而减小；β＞65°时面积质量因子j/f随着波纹倾角β的增大逐渐增大；β=30°时j/f达到最大，β=65°时j/f达到最小。另外，随雷诺数Re的增大，面积质量因子j/f有逐渐减小的趋势，也即综合换热性能有所降低，因此应使流速尽量降低。 总体上，波纹倾角越小，综合换热性能越高。

3.2 波纹间距

对于波纹倾角β=65°、波纹高度H=3 mm的波纹板，在不同的波纹间距λ下，努塞尔数Nu、摩擦阻力系数f和面积质量因子j/f随雷诺数Re的变化规律如图6所示。

图6 不同λ下的Nu、f和j/f随Re的变化规律

由图6a可见：当波纹间距λ相同时，波纹板的努塞尔数Nu随着流体雷诺数Re的增大而增大；当流体雷诺数Re不变时，波纹板的努塞尔数Nu随着波纹间距λ的增大而减小，且减小趋势减弱，波纹间距λ越小时，波纹板的努塞尔数Nu随着流体雷诺数Re的增大趋势较为明显， 但随着波纹间距λ的增大，增大趋势较为减弱。 这是由于波纹间距的大小直接影响了波纹板间的接触面数目的多少，波纹间距越小时，波纹板间的接触面数目增多，使流体的湍流强度增强，换热性能增加。

由图6b可见：当波纹间距λ相同时，摩擦阻力系数f随着板间流体雷诺数Re的增大逐渐减小，且递减速率逐步减小； 当流体雷诺数Re不变时，摩擦阻力系数f随着波纹间距λ的增大而减小。 这是由于波纹间距逐渐增大时，波纹板间的接触面数目逐渐减少， 沿波纹方向的动量分量也不断减小，导致波纹板流道内的流动阻力减小，摩擦阻力系数也减小

由图6c可见：面积质量因子j/f随着波纹间距λ的增大而增大，且增大幅度逐渐变大，波纹间距λ=14 mm时，面积质量因子j/f最大，这表明波纹间距λ越大，综合换热性能越高；随着波纹间距的增大，传热因子的减小程度要远小于摩擦阻力系数的减小程度，故面积质量因子随着波纹间距的增大而逐渐增大；面积质量因子随着流体雷诺数的增大缓慢减小，流体流速较小时有助于增强综合换热性能。

3.3 波纹高度

对于给定波纹倾角β=65°、波纹间距λ=11 mm的波纹板，在不同的波纹高度H下，努塞尔数Nu、摩擦阻力系数f和面积质量因子j/f随雷诺数Re的变化规律如图7所示。

由图7a可见：在给定波纹高度H下，波纹板的努塞尔数Nu随着流体雷诺数Re的增大逐渐增大；在同一雷诺数Re下，随着波纹高度H的增大，努塞尔数Nu逐渐增大，且增大程度减弱。 这是由于随着波纹高度的增大，流道空间增大，流体流动逐渐均匀，由“曲折流”转变成“十字交叉流”，致使流体在板间接触面处的流动死区减少，提高了换热效率。

图7 不同H下的Nu、f和j/f随Re的变化规律

由图7b可见：随着波纹高度H的增大，波纹板的摩擦阻力系数f逐渐增大， 且增大幅度逐渐减小；在各个波纹高度H下，波纹板的摩擦阻力系数f随流体雷诺数Re的增大呈逐渐减小的趋势。 这是由于当量直径增大，流体沿波纹方向的动量分量逐渐增大，在流道空间中流动均匀，压降损失减少。

从图7c可见： 面积质量因子j/f随波纹高度H的增大而减小，且减小幅度逐渐降低；在各个波纹高度H下， 面积质量因子j/f随着流体雷诺数Re的增大缓慢减低。 这是由于随着波纹高度的增大，传热因子的增大程度要大于摩擦阻力系数的增大程度，从而使面积质量因子随着波纹高度的增大而逐渐增大。 由此表明，波纹高度对波纹板换热器的综合性能的影响较为明显。

4 波纹板的结构参数对板片的力学性能的影响分析

4.1 波纹倾角

为研究波纹倾角对波纹板片力学性能的影响，针对6组流速，分别算得波纹板片的最大变形量和最大等效应力随波纹倾角的变化规律（图8）。

图8 板片的力学性能随波纹倾角的变化规律

由图8可见：同一流速下，波纹板片的最大变形量和最大等效应力随波纹倾角的增大先增大后减小（这是由于随着波纹倾角的增大，波纹板间的接触面数目不断减少，造成板间流体对波纹板的压力是先增大后减小，从而使波纹板最大变形量和最大等效应力呈现先增大后减小的趋势）；在各个波纹倾角下，波纹板片的最大变形量和最大等效应力随着流速的增大而增大；波纹倾角为65°时，波纹板片的最大变形量和最大等效应力均达到顶峰。

4.2 波纹间距

针对6组流速， 分别算得波纹板片的最大变形量和最大等效应力随不同波纹间距变化规律（图9）。

图9 板片的力学性能随波纹间距的变化规律

由图9可见， 波纹板片的最大变形量和最大等效应力随波纹间距的增大逐渐减小，且减小程度显著；在各个波纹间距下，波纹板片的最大变形量和最大等效应力随着流速的增大而增大。 另外，波纹间距9 mm时，波纹板片的最大变形量和最大等效应力达到顶峰；波纹间距14 mm时，波纹板片的最大变形量和最大等效应力降到低谷。 由此可见，较小的波纹间距对波纹板片受力影响较大。 这是由于增大波纹间距，波纹板间的接触面数目不断减少，湍流强度减低，导致流体对波纹板的压力逐渐减小，从而使波纹板的最大变形量和最大等效应力逐渐减小。

4.3 波纹高度

针对6组流速， 分别算得波纹板片的最大变形量和最大等效应力随不同波纹高度变化规律（图10）。

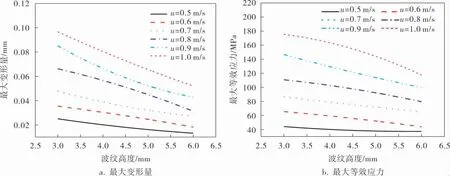
图10 板片的力学性能随波纹高度的变化规律

由图10可知，随着波纹高度的增大，波纹板的最大变形量和最大等效应力逐渐减小。 波纹高度3 mm时，波纹板的最大变形量和最大等效应力值达到顶峰；波纹高度6 mm时，波纹板的最大变形量和最大等效应力值降到低谷。 因为波纹高度越高，流道的空间越大，波纹板间的接触面对流体的流动影响较小， 使流体在板间流动更加均匀，受到的流动阻力逐渐减小，所以作用于板上的压力载荷减小，致使波纹板片的最大变形量和最大等效应力降低。

5 结论

5.1 随着波纹倾角的增大， 努塞尔数先增大后减小、摩擦阻力系数先增大后减小，波纹倾角在65°附近的传热效果最好；随着波纹间距的增大，努塞尔数减小且减小趋势逐渐减弱，摩擦阻力系数逐渐减小且递减速率逐步减小；随着波纹高度的增大，流道空间增大，流体流动更加均匀，致使努塞尔数和摩擦阻力系数均逐渐增大。

5.2 采用面积质量因子法对板片进行综合性能评价——面积质量因子，随着波纹倾角的增大而减小、随着波纹间距的增大而增大且随着波纹高度的增大而减小。

5.3 随着波纹夹角的增大， 波纹板片的最大变形量和最大等效应力随波纹倾角的增大先增大后减小， 波纹倾角65°时波纹板片的最大变形量和最大等效应力均达到顶峰；随着波纹间距的增大，波纹板片的最大变形量和最大等效应力逐渐减小；随着波纹高度的增大，波纹板片的最大变形量和最大等效应力逐渐减小。