Non-integer Order Control Scheme for Pressurized Water Reactor Core Power

Ibrahim M.Mehedi, Maher H.AL-Sereihy, Asmaa Ubaid Al-Saggafand Ubaid M.Al-Saggaf1,

1Department of Electrical and Computer Engineering (ECE), King Abdulaziz University, Jeddah, 21589, Saudi Arabia

2Center of Excellence in Intelligent Engineering Systems (CEIES), King Abdulaziz University, Jeddah, 21589, Saudi Arabia

Abstract: Tracking load changes in a pressurized water reactor (PWR) with the help of an efficient core power control scheme in a nuclear power station is very important.The reason is that it is challenging to maintain a stable core power according to the reference value within an acceptable tolerance for the safety of PWR.To overcome the uncertainties, a non-integer-based fractional order control method is demonstrated to control the core power of PWR.The available dynamic model of the reactor core is used in this analysis.Core power is controlled using a modified state feedback approach with a non-integer integral scheme through two different approximations, CRONE(Commande Robusted’Ordre Non Entier,meaning Non-integerorder Robust Control) and FOMCON (non-integer order modeling and control).Simulation results are produced using MATLAB®program.Both non-integer results are compared with an integer order PI (Proportional Integral) algorithm to justify the effectivenessof the proposed scheme.Sate-space model Core power control Non-integer control Pressurized water reactor PI controller CRONE FOMCON.

Keywords: Sate-space model; core power control; non-integer control;pressurized water reactor; PI controller; CRONE FOMCON

1 Introduction

Nuclear power generation is a cost-competitive source of clean energy.It provides a stable baseload of energy.It can easily be coupled with other renewable sources of energy such as solar and wind as per their availability.The energy production from a nuclear plant can be lowered or cranked up according to the availability of good wind or solar resources and the high demand for electricity at the load.A Nuclear power has a lower environmental impact than other energy harnessing methods of energy generation.Although nuclear power station is very advantageous, the waste produced is dangerous for both humans and the environment.Beyond these threats, security issues are also crucial to consider while producing nuclear energy.In particular, nuclear power plants equipped with pressurized water reactors (PWRs) are very concerned with controlling their power output while changing their loads.It is really a challenge to design an effective control system to regulate the core power due to its sensitivity and time-varying phenomena.As one of many control techniques, the percent integration differentiation controller (PID) is very popular in both industrial control and nuclear power plant core power control.However, there are some tuning issues for the PID control method to fulfill the exact requirement for core power control [1].There are some other control methods such as,fuzzy logic methods [2], intelligent control methods [3], neural network techniques [4], axial offset strategy [5], optimal control system [6] and State-space model-based predictive control methods [7],that demonstrate the core power control in PWRbased nuclear power stations.Due to the sensitivity of its reactor, the researchers had difficulty controlling the core power even after completing a successful demonstration.Consequently, there are scopes for better control schemes to be demonstrated for the purpose of core power control in a pressurized water reactor while following the required load changes.

Non-integer control, also known as fractional order control (FOC), has attracted much attention in control engineering due to its powerful performance tuning range and controllability over timevarying systems[8,9].The performance is especially increased in contrast to traditional PID controllers by utilizing non-integer calculus.Several recent papers [8-11] have investigated this fact.The noninteger order controllers have numerous advantages because of their easy design criteria and ease of implementation.They can be employed commonly in different types of systems for industrial automation as well.Robustness is also ensured for the controllers containing non-integer filters.

An approach to control core power in pressurized water reactors based on non-integer order control is presented in this paper.The state-space model is chosen based on differential equations considering thermal-hydraulic models, neutron dynamics models, and reactivity models.Core power is controlled using a modified state feedback approach with a non-integer integral scheme through two different approximations, CRONE (Commande Robuste d’Ordre Non Entier, meaning Non-integerorder Robust Control) and FOMCON (non-integer-order modeling and control).The proposed noninteger order control approaches produced better performances than that of the integer-order control method.Comparative simulation results are demonstrated in this current investigation.

This paper continues as follows: In Section 2, we discuss basic concepts of dynamic models for pressurized water reactors.Non-integer order control scheme is described in Section3.The state-space dynamicmodel of reactor core power control is presented in Section 4.Section 5 presents the computer simulation results obtained using MATLAB®program.Comparisons of integer and non-integer order control schemes are also provided in this Section.Finally, Section 6 concludes the paper with a brief discussion.

2 Dynamics Models of PWRs

Three dynamic models are combined to model the core power dynamics system of PWRs.These include a dynamic model using neutron analysis, hydraulic model using thermal analysis, and reactivity model for pressurized water reactors [12-16].

2.1 Dynamics Models Based on Neutron Analysis

Neutron dynamic model is considered the primary step for the dynamics modeling of water reactors.Due to the reduced computational workload,multi-group delayed neutrons are consolidated into one group [4].The simplified dynamic equation for the rate of neutron density and the concentration of delayed neutrons are as follows:

Here,qanddare the rates of change of neutron density and the rate of change of concentration of delayed neutron, respectively.The other symbols σ,∀and μ stand for reactivity, required time to generate a neutron, and the decay constant for the delayed neutron.Moreover,γ is the total effective fractional delayed neutrons.Now the above kinematic equations are expressed as follows:

Therefore, the real-time core power,Qr(t) is defined as the product of nominal core powerQ0and the neutron density,q:

It is assumed that the nominal core power remains constant, therefore,qis represented as relative core power.

2.2 Hydraulic Models Based on Thermal Analysis

Similarly, the thermal-hydraulic models are defined accounting for energy conservation [7].Based on this model, the cooling water transfers heat to the secondary circuit and the fuel transfers heat to the cooling water, using heat transfer coefficientsQh(t) andQs(t).Therefore, the energy conservation equations are obtained as follows:

In this instance,Mrepresents the mass flow rate of cooling water at a given heat capacity, while C represents the coefficient of heat transfer from fuel to cooling water.TfandTware the average temperatures of the fuel and cooling water.The temperature of cooling water at the inlet and outlet isTiandTo.Temperature differences between the inlet and outlet of cooling water are assumed to be constant.Therefore, we would expect that this value will hover between 300°C and 330°C.The thermal transfer between fuel and cooling water was assumed to occur with other cooling water parameters unchanged.Consequently, the inlet temperature does not deviate from its point of balance, i.e.,ΔTi=0.Calculate the average cooling water temperature using the formula(Ti+To).Heat is transferred from the fuel to the cooling water by using the following dynamic equations:

where φcis cooling water heat capacity,ffis the fraction quantity power stored in reactor fuel and φfis the fuel heat capacity.

2.3 Reactivity Models of PWRs

The reactive models are introduced in [17].By moving the control rod, the reactivity is achieved.It is the product of total reactivity worth of control rod,Hrand the velocity of the control rod,Jras shown here:

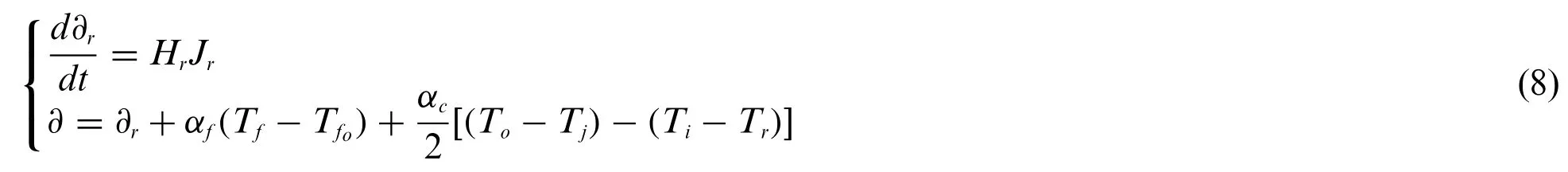
Here,αcand αfare the reactivity coefficient of cooling water and fuel of PWRs.Tfo,Tj, andTrare initial temperatures of steady-state fuel, the inlet of cooling water, and outlet of cooling water,respectively.It is already assumed that there is no change in the inlet temperature of cooling water from the point of balance.Therefore, the following equation is achieved.

3 Scheme Using Fractional Order Integral Action

In order to enhance the tracking attainments and disturbance rejection, fractional order integral control with state feedback control is very valuable [18].The state-space expression for linear timeinvariant (LTI) systems is as follows:

Here, the state vector is denoted byx(t)∈Rnand matrixA∈Rn×nis called the coefficient matrix.u(t)∈R andy(t)∈R are the input and output signals.q(t)∈R is for disturbance input.The control gain vector and out vector are denoted by column matricesB∈Rn×1andC∈R1×n, respectively.Control laws are written as follows if the integral control is incorporated:

whereX(t) = [x(t)xr(t)]’is the augmented state vector andxr(t) is the output of the integral action.

Among several suitable methods, Ackermann’s formula is widely used to evaluate the state feedback vector gain,Kp, andKr.Actually, the state feedback control helps to locate the suitable positions of the poles.For this reason, a non-integer order integrator, 1/sαmay be used to reduce the effects of zeros during transient responses.In this case, the static gainKrwill be changed by a compensatorK(s).Further, the state feed-back gainKsis utilized to stabilize the system, and a cascaded compensator,K(s) is used along the forward path of 1/sαin order to enhance the transient performance of the closed-loop system as shown in Fig.1.It introduces the concept of non-integer order control architecture.In this case, Bode’s ideal transfer function [9] is utilized as an open-loop reference model to designK(s) of Fig.1.It entails the opportunity of variable gains so that the robust closed-loop system is ensured exhibiting the iso-damping properties in step response.

Figure 1: Non-integer compensator based state feedback control

Bode’s ideal method uses the following closed-loop transfer function:

Here, the performance of tracking system depends on υcfor transient conditions and η is responsible for overshoot.It is mentioned in [9] that the gain crossover frequency ωcand the phase margin φmare used to calculate υcand η.

An underdamped behaviour is obtained for step response of Eq.(12) which has range of damping ratio from zero to one.The value of η is calculated by the Eq.(14) [9].

Here,Mp(%) is the maximum overshoot.It can be mentioned that the state feedback gain,Ksis suitable for the stable systems as well as unstable systems.The detailed design of the integer filter gain,(K(s))and state feedback gain,(Ks)are available in[19].Now the control law of the architecture shown in Fig.1 is as follows:

Here, the derivation of non-integer order is evaluated by the following equation of an integral operator,Dμ[9]:

This non-integer order integral operator,Dμis used to produce new state,xrwith respect to the reference parameters,r.Actually,fractional integrator,integrates the tracking error to producexr.In Eq.(15),K(t) is the impulse response ofK(s).This is added through convolution with the gain vector,Ks.Once again, an integration of power μ(μ=η) is cascaded withK(s), to establish the closed-loop ideal transfer function of Eq.(12).

The vectorKsplaces arbitrarily the number of characteristic roots of inner-loop as follows:

Ackermann’s technique [19] is used to calculate the characteristic roots.The integer filterK(s) is evaluated by

In Eq.(10),N(s) is the numerator of the linearized system.A low pass filter,is incorporated to makeK(s) more realizable.The explanation and proof ofK(s) are available in [19].

4 State-space Model of Core Power Control

The non-integer order control scheme applied in core power control is based on the non-integer order theory of calculus.In this regard, the state-space based mathematical model is considered for the pressurized reactor core.The model is described as follows [20]:

Here,xis state variables and˙xis its derivatives.The output variable is expressed byyanduis the control variable of the state space.Coefficient matrices are expressed byA, B, CandD.

According to the slow perturbation theory, deviation of neutron density,∂qis very small than the balance value,q0.The neutron density equation is expressed as follows:

Therefore, the Eq.(3) is simplified and linearized as bellow [13]:

The state variables of this model is

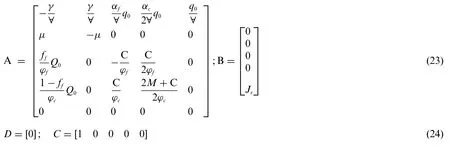
As an output variable we consider the deviation value of neutron density,∂q, and the control rod velocity,Jras the control input.With the help of linear algebra and differential geometry, the coefficient matrices are deduced as follows [21]:

5 Non-integer Order Control Approximation

Controlling of core power in nuclear power stations with pressurized water reactors is demonstrated using PI control of non-integer order.A controller design that does not track the changes in the level of core power can be more flexible using non-integer order controllers.

The proposed non-integer PI controller is approximated through two different approximations; CRONE, developed by A.Oustaloup, and Non-integer order modeling and control (FOMCON); a MATLAB®toolbox [22].The current investigation focuses on these two non-integer order approximations.

5.1 CRONE

CRONE (Commande Robuste d’Ordre Non Entier, meaning Non-integer-order Robust Control)controller developed by A.Oustaloup [9].It is a MATLAB and Simulink toolbox designed for a noninteger controller and developed by the CRONE team.Some Some Methods in the CRONE toolbox for noninteger MIMO transfer functions can be implemented in an object-oriented version for the tool.The CRONE toolkit is used by several toolboxes, such as.Ninteger and FOMCON [23,24].The transfer function using Ninteger toolbox of CRONE approximation is shown as follows [25]:

Functions in frequency domain are processed by this function.ωznand ωpndepend on the domain of working frequency [ωh,ωl] andk′is an adjustable gain.

5.2 FOMCON

The FOMCON (non-integer-order modelling and control) is MATLAB toolbox developed by Tepljakov, Petlenkov, and Belikov [23,24,26].This unit is based on mini toolbox, FOTF.The details of“FOTF”can be found at [27].FOMCON offers graphical user interfaces (GUIs), Simulink blocks,system identification, and control design functionality.FOMCON’s relationship to other toolboxes is shown in Fig.2 [28].

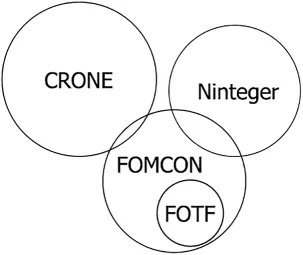
Figure 2: Other tool boxes related to FOMCON

6 Simulation Results

Due to the sensitivity of the nuclear reactor, it is difficult to follow the core power according to load changes.In order to justify the performance of the proposed control method, simulations of the non-integer PI controller were designed to compare with the integer PI controller.Tab.1 shows the prime constraints of PWR for the purpose of this investigation.

Table 1: PWR’s constraints for computer simulation

The linearized model, composed of the values shown in Tab.1, along with other necessary numerical values, can be described this way:

Two different numerical toolboxes are used to approximate the non-integer integral.Here,α is non-integer operator.Chosen frequency domain limits are ωl=10 and ωh=1000.Adjusted gaink’is 1.Both CRONE and FOMCON toolboxes provide integrator blocks in Simulink, which makes the simulation easier.

Simulated results indicate good performance of the non-integer PI controller for core power control compared to the integer PI controller.Fig.3 shows tracking the performance of non-integer PI using CRONE and FOMCON approximation.The desired core power level was deferring from 100%→60%→100% of nominal core power.

Figure 3: Tracking performance of non-integer PI (100%→60%→100%)

It is observed that two numerical approximations are used to implement the non-integer order integrator.The proposed non-integer PI controller improves the performance in terms of tracking error and rise time.However, CRONE appears to be faster than FOMCON in terms of rising time.

As depicted in Fig.4 the performance of the non-integer PI controller was tracked for the expected core power deffer from 50%→60%→50% nominal core power.

Figure 4: Tracking performance of non-integer PI (50%→60%→50%)

Figs.5 and 6 show the effectiveness of the proposed non-integer PI controller compared to the integer PI controller.In Fig.5, the expected core power value was deferring from 50%→60%→50 of core power at nominal value, and in Fig.6, the expected core power level was differing from 0%→10%→0% of nominal core power.

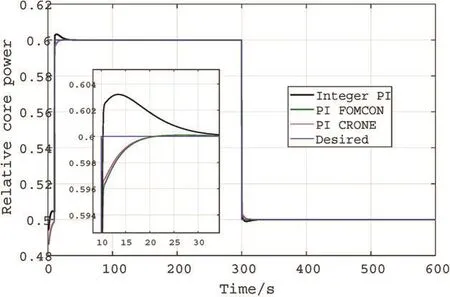
Figure 5: Tracking performance of non-integer PI (50%→60%→50%)

Figure 6: Tracking performance of non-integer PI (0%→10%→0%)

We can see that the proposed non-integer PI controller improved control performance and has better performance than integer PI in terms of tracking error and overshoot.

7 Conclusion

This paper presented non-integer order control methods to regulate the core power of the pressurized water reactor for nuclear power stations.This non-traditional control method possesses a high-performance tuning range.Designing this non-integer order controller is not cumbersome.Moreover, the ease of its implementation has made it an attractive choice.The non-integer order control methods are also commonly employed in industrial automation.Ensuring robustness is anadditional advantage of a non-integer controller.Therefore, the non-integer order control method is very useful for core power control in PWR.State-space analysis of the reactor core was used to develop the proposed control technique.The simulation results illustrate the usefulness and improved stability of the non-integer order state-space method.The proposed control technique can react swiftly to the changes of load and thus tracking error is reduced promptly and efficiently.The effectiveness of the proposed non-integer order methods is justified through a performance comparison with the integerorder PI control method.In addition, robustness is ensured by the proposed control scheme.

Acknowledgement:This project was funded by the Deanship of Scientific Research (DSR), King Abdulaziz University, Jeddah, Saudi Arabia under grant no.(KEP-Msc-36-135-38).The authors,therefore, acknowledge with thanks DSR technical and financial support.

Funding Statement:This project was funded by the Deanship of Scientific Research (DSR), King Abdulaziz University, Jeddah, Saudi Arabia under grant no.(KEP-Msc-36-135-38).

Conflicts of Interest:The authors declare that they have no conflicts of interest to report regarding the present study.