点载荷作用下煤岩颗粒断裂强度的试验研究

潘永泰，李泽康，周 强，柳铭哲，庄梓巍，庞 雷，廖璐铭

(1.中国矿业大学(北京) 化学与环境工程学院，北京 100083；2.昆明理工大学 国土资源工程学院，云南 昆明 650093)

分级破碎机以其处理量大、分选效率高以及过粉碎率低等优点占据煤炭破碎行业的绝大部分市场[1]。它兼具破碎与筛分的功能，工作时只对大于粒级要求的部分进行破碎，小于粒级要求的部分则从齿尖与齿辊的间隙顺利通过，从而达到严格控制产品粒度的效果。分级破碎产品的粒度分布是影响后续流程分选效率的重要因素，但对其的预测缺乏相关理论指导[2]。研究表明，决定产品粒度的关键因素之一为入料的断裂强度[3]，实现分级破碎过程中入料断裂强度分布模型的准确描述是预测分级破碎过程中产品粒度分布的重要步骤。

在不同加载方式下，颗粒的断裂强度是不同的。在以挤压破碎为主的颚式、圆锥破碎机中，断裂强度可通过压力试验机测得[4，5]；在以冲击破碎为主的冲击式、锤式破碎机中，断裂强度可通过霍普金森压杆试验[6，7]、落重试验[8]和摆锤试验[9]测得；而对于以劈裂、刺破为主要破碎方式的分级破碎机，有学者通过仿真方法得到颗粒的断裂强度[10]，但很少人通过试验的方法直接测得。由于分级破碎过程大多为破碎齿将物料刺破，这种破碎形式与点载荷仪对物料的破坏类似，故可通过点载荷仪测定分级破碎机破碎过程中颗粒的断裂强度。

通过点载荷仪测定煤岩颗粒的最大破碎力(颗粒上下接触点之间出现裂隙时对应的载荷)与断裂应力(最大破碎力与断裂面积的比值)，以此来定义其分级破碎时的断裂强度。由于材料内部随机分布孔洞、裂隙和杂质等缺陷，使得其强度具有离散性[11]，利用4种常用于描述脆性物料强度分布的统计学模型：Boltzmann模型、Weibull模型、Lognormal模型和Logistic模型对同组煤岩颗粒的断裂强度进行拟合，选取最合适的模型建立模型参数与颗粒尺寸之间的关系式，得到煤岩颗粒分级破碎时的断裂强度分布模型。该模型为实现分级破碎过程中产品粒度分布的预测提供理论依据。

1 试验方案

1.1 试验设备

本试验使用的设备型号为HDH-1型岩石点荷载仪，如图1所示。该试验设备可施加最大点载荷为50kN，精确度为10N。试验时将试件置于两个圆锥状(圆锥球端曲率为5mm，圆锥顶角为60°，材质为工具钢，HRC大于60)的压板之间，对试件施加载荷直至破坏，根据破坏时的载荷计算试件的断裂强度。操作过程：①放置好物料后，快速加载，使得物料快速上升至与上锥头接近位置；②上锥头与物料将要接触时，缓慢加载直至破坏，避免产生惯性效应。

图1 HDH-1型岩石点荷载仪

1.2 试验材料

本试验选取材料为阳煤集团的矸石与准格尔旗矿区的烟煤。矸石的主要成分为高岭石、伊利石、石英及黄铁矿等矿物；烟煤的有机组分主要是均质镜质体，无机组分主要为黏土和黄铁矿。两种材料的物理参数见表1。试验前，测量并记录每个颗粒加载方向的直径，并以此作为粒级划分标准，将烟煤与矸石颗粒划分为0～10mm、10～20mm、20～30mm、30～40mm四个粒级。此外，选取几何形状相似的颗粒以降低自身形状对试验结果的影响。

在加载过程中，试验进行到颗粒的上下接触点之间出现图1所示的贯穿性裂隙为止，记录破坏时最大的点载荷。由于颗粒内部结构的复杂性，需选取大量的样本进行试验，以获得一条可靠的强度分布曲线。本次试验共选择540个粒径为0～40mm的烟煤与煤矸石颗粒进行点载荷试验，其中无效试验(颗粒部分断裂，结果存在误差)共计40组，对500组有效数据进行分析。

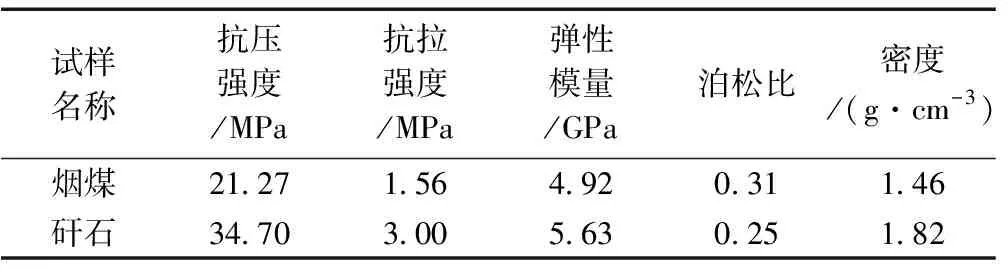
表1 烟煤与煤矸石的基本物理参数

2 结果及讨论

2.1 原始煤岩颗粒的断裂强度分布

关于颗粒的强度，学者们的定义主要分为以下4种[12-18]：破碎力、断裂能、断裂应力和断裂比能。计算破碎力与断裂应力的方法较为简便，因此选取最大破碎力与断裂应力来定义颗粒强度。最大破碎力为试样出现贯穿性裂隙时对应的点载荷，其示数可从显示仪中直接读取。计算断裂应力的经验公式有很多[5]，基于点载荷实际工况，选择式(1)计算颗粒的断裂应力。

σc=Fc/d2

(1)

式中，d为压头与物料接触时，两压头之间的距离，mm；Fc为最大破碎力对应点载荷，N。

为得到合理的煤岩颗粒强度分布，需要对大量的样品进行试验。基于试验的可行性，引入概率估算因子P计算断裂概率[19]。

式中，i是某颗粒强度在全部试样强度按升序排列中的排名；n是样品个数。

四种不同粒级的烟煤与煤矸石颗粒强度(破碎力、断裂应力)分布如图2所示。由图2可知，试验数据的原始分布规律随尺寸的变化而变化，主要原因是颗粒内部随机分布着大小不一的裂纹，受力后扩展的方向不受控制。点载荷随着颗粒尺寸的增加，离散性越大；而断裂应力随着颗粒尺寸的增加，离散性越小。

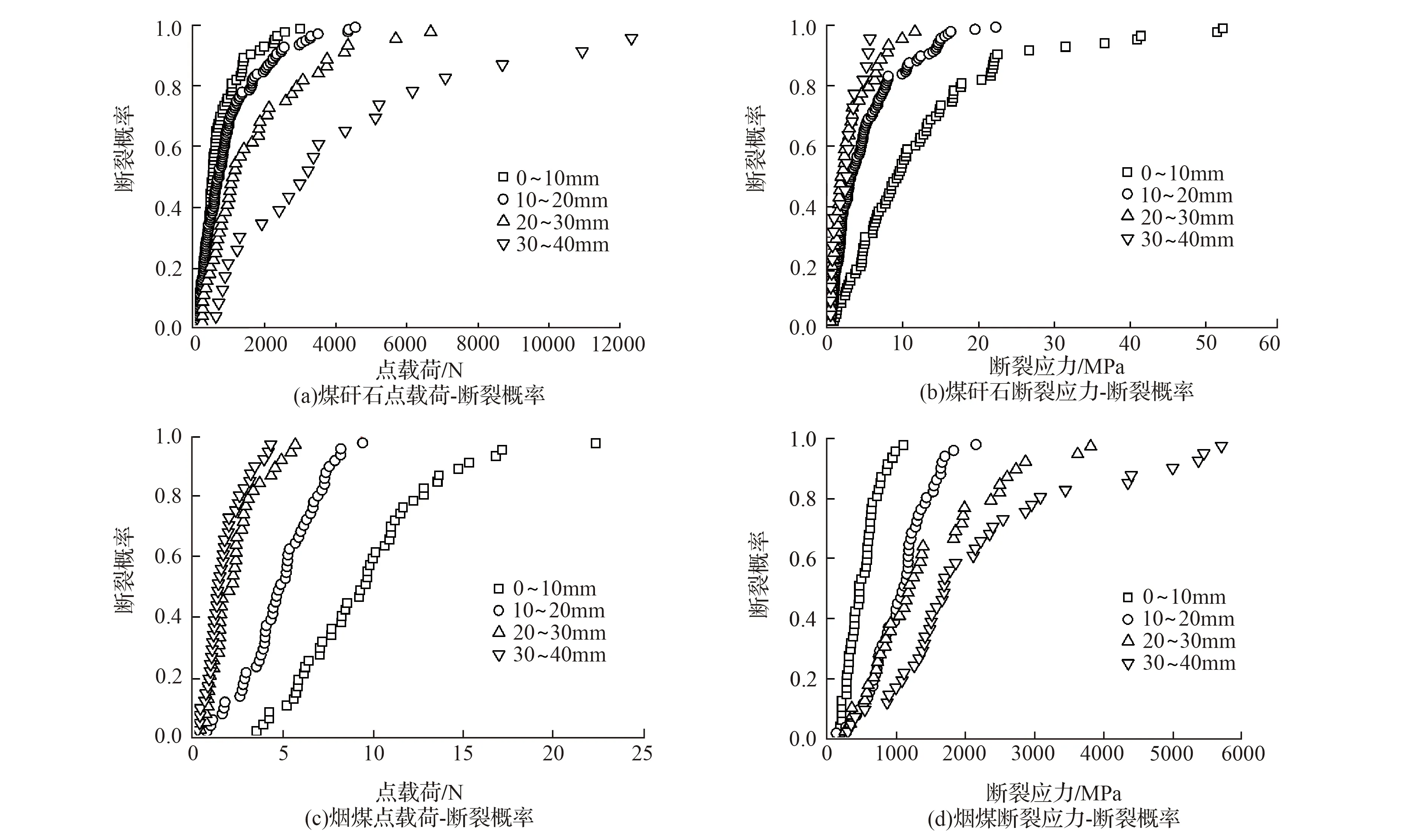
图2 原始煤岩颗粒强度分布

2.2 煤岩颗粒断裂强度分布模型的选取

煤岩颗粒强度分布具有离散性，为对试验数据进行合理描述，本文使用四种常见模型对试验数据进行拟合，其函数形式为：Logistic模型式(3)、Weibull模型式(4)、Lognormal模型式(5)与Boltzmann模型式(6)。

式(3)—式(6)中，Fc为点载荷，N；a、b、A1、A2、F0与δ为模型参数。把式(3)—(6)中Fc替换为σc，则为断裂应力定义断裂强度的表达式。用式(3)—(6)拟合图2(a)中强度分布试验数据，以此来对比4种模型的拟合效果，结果如图3所示，模型参数及相关系数见表2。

图3 试验数据与拟合曲线的比较

由图3可知，4种模型均能较好的描述点载荷作用下煤矸石颗粒的强度分布，为了进一步比较拟合效果，将不同函数的模型参数与相关系数R2列于表2。由表2可知，Logistic模型、Lognormal模型与Boltzmann模型的拟合R2分别为0.991、0.991与0.992，均高于Weibull模型拟合R2，0.987。对前3种模型综合比较可得：Logistic模型相比Lognormal模型与Boltzmann模型，其表达形式简单，模型参数与颗粒断裂概率具有对应关系。其中，a表示颗粒的中值强度，即断裂概率为0.5时的断裂强度；b表示离散程度。最终选择Logistic模型拟合煤岩颗粒强度分布数据。

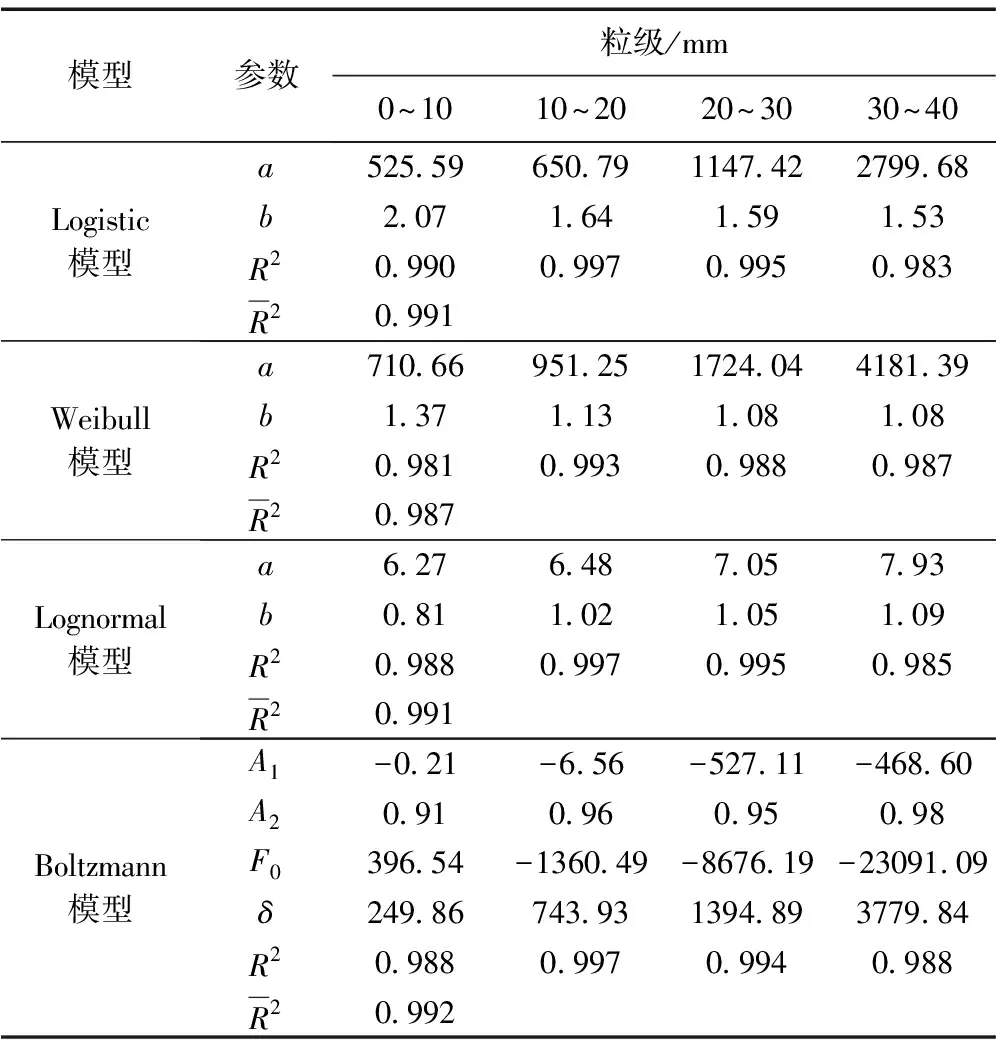
表2 模型参数及相关系数

将式(3)中参数a、b替换为F50(σ50)、DF(Dσ)，再通过移项转化为分别以点载荷与断裂应力定义断裂强度的表达式，即式(7)、式(8)。

式中，F50为中值强度对应的点载荷，N；σ50为中值强度对应的断裂应力，MPa；SF、Sσ分别为以点载荷与断裂应力定义强度分布的断裂概率；DF、Dσ以点载荷和断裂应力定义强度分布的离散程度。

2.3 断裂强度分布模型的验证及扩展

不同粒级煤矸石与烟煤的Logistic模型拟合详细数据见表3，拟合曲线与试验数据的吻合度均较好。为了进一步扩展断裂强度分布模型，建立式(7)(8)中参数DF、Dσ、F50和σ50与颗粒尺寸之间的关系式。煤矸石与烟煤的不同粒级的DF和Dσ关系如图4所示，可以看出随着颗粒尺寸的增加，DF和Dσ没有表现出对粒度有明显的依赖性，与其他学者得到的试验结果相同[20]，故认为DF和Dσ是个常数或与粒度呈现弱函数关系。煤矸石的DF和Dσ的变化范围分别为1.53～2.07，1.39～1.80，均值分别为1.71与1.56；而烟煤的DF和Dσ的变化范围分别为2.24～3.05，2.35～3.87，均值分别为2.90与3.12；不同粒级烟煤的DF和Dσ均大于煤矸石的DF和Dσ，说明烟煤强度的离散程度较小，材料的均质性较高。

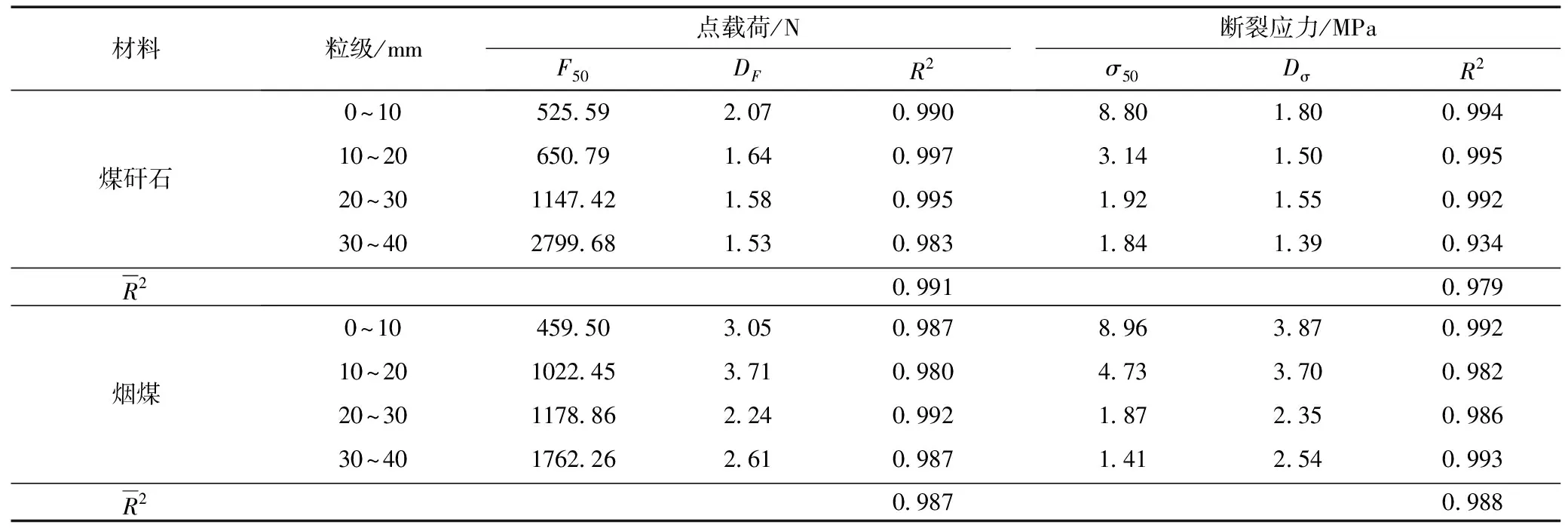
表3 四种粒级煤矸石与烟煤的拟合结果

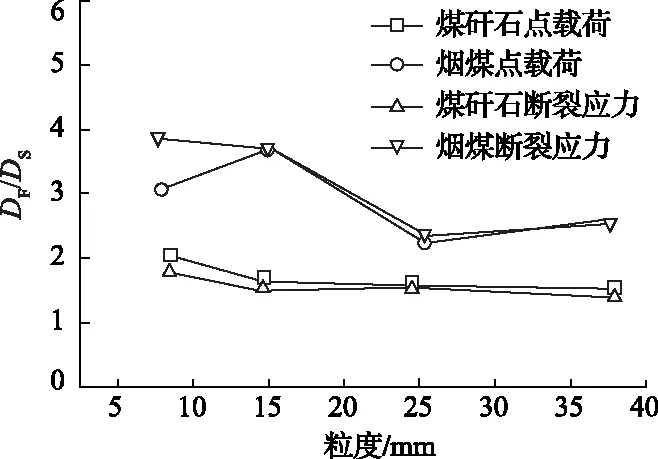
图4 DF、Dσ与粒度的关系

对模型中的F50与σ50进行研究，结果如图5、图6所示。由图5可知，F50与粒度呈幂函数规律增加，即颗粒的尺寸越大，F50也随之增加。由图7可知，σ50与粒度呈幂函数规律减小，即颗粒的尺寸越大，σ50也随之降低。试验现象与“尺寸效应”规律一致，即颗粒越小越难破碎。综合上述研究，最终的煤矸石与烟煤的分级破碎断裂强度分布模型整理如下。

图5 煤矸石与烟煤的F50与粒度的关系

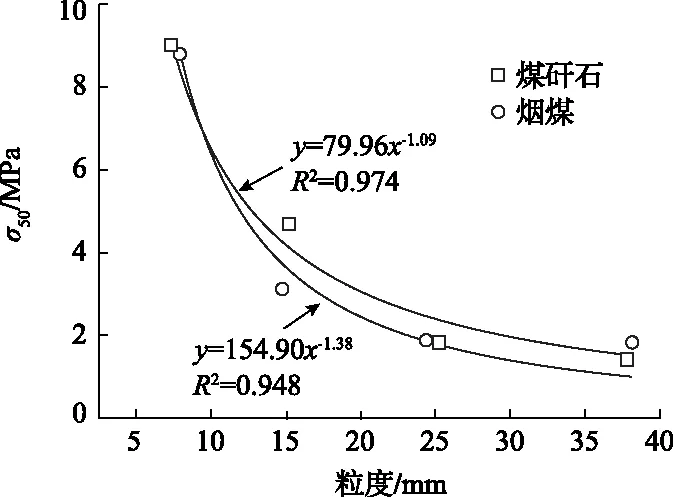
图6 煤矸石与烟煤的σ50与粒度的关系

3 结 论

1)选取点载荷仪来测定煤岩颗粒分级破碎时的断裂强度。综合考虑Logistic模型、Weibull模型、Lognormal模型与Boltzmann模型对点载荷作用下煤岩颗粒断裂强度分布数据的拟合效果与表达式的难易程度，最终确定Logistic模型更适合构建为煤岩颗粒分级破碎的断裂强度分布模型。

2)Logistic模型中，煤岩颗粒的离散程度与其尺寸没有明显的依赖关系，可认为只与自身的特性相关；煤岩颗粒中值强度对应的点载荷随颗粒尺寸的增加呈幂函数规律增加，而中值强度对应的断裂应力随颗粒尺寸的增加呈幂函数规律减小。

3)通过扩展Logistic模型，建立了煤岩颗粒分级破碎断裂强度分布模型，为进一步建立预测分级破碎产品粒度分布的数学模型提供理论依据。