基于BP神经网络与数据拟合的接收信号强度测距算法比较研究及算法实现
2022-08-24叶扩会尹国成
叶扩会,尹国成
(保山学院,云南 保山 678000)
0 引言
无线传感器在军事领域及工业领域有极其重要的作用。定位技术是无线传感器网络的关键技术之一。定位技术的发展成为学术界和产业界关注的热点[1-4]。
目前,定位技术的研究主要分为两大方向:基于测距和基于非测距的定位算法。基于测距算法研究的方向大致有:基于到达时间(TOA)、基于到达时间差(TDOA)、基于到达角度(AOA)、基于接收信号强度(RSSI)。基于RSSI方法具有硬件设备简单、成本低等优点。因此,该方法在室内定位中得到了广泛的应用,但RSSI测距受环境影响较大,如何较为精确地估计信号强度与距离之间的关系,在定位技术中有着至关重要的作用[5]。本文将研究数据拟合测距及BP神经网络测距,并比较两种方法的测距效果。
1 RSSI测距模型理论基础
1.1 数据拟合及其参数估计
影响信号的传播的因素很多,如多径、障碍物、折射、噪声等[6,7,9,10]。在特定的环境中,无线信号传输主要受传输距离的影响。经典理论模型有对数-常态分布模型[1-3]:
RSSI=P(d)=A-10nlgd
(1)
式中:A是测试距离d0=1处接收到发射节点的信号强度值。
本文将利用最小二乘法理论,对参数A,n进行估计。其思想是记录多个已知节点距离发射节点的距离和接收到的信号强度,运用数据拟合理论[6],估计参数A,n。即用已知节点数据估计参数,从而求出未知位置。步骤如下:
(1)取k个已经节点i(i=1,2,…,k),测量节点i(i=1,2,…,k)到发射节点的距离di及接收到的信号强度RSSIi;
(2)将di代入(2)式可得模型预测值
RSSIi′=A-10nlgdi;
(3)求误差平方和
(4)由J最小,建立如下方程组
从而求得参数A,n。
将(1)式变形为如下测距模型[11]
(2)
1.2 BP神经网络结构
由映射网络存在(Kolmogorov)定理可知,任意一个连续的函数都可以由一个3层的 BP神经网络实现[1,8]。BP神经网络主要有输入层、隐含层、输出层组成。本文采用的BP神经网结构,如图1所示。

图1 BP神经网结构
2 实验与结果分析
2.1 实验数据
为模拟实验,本文将家用路由器放到室内4 m×10 m区域指定位置,每隔0.2 m,用手机自带测量信号强度功能,测量距离路由器为di(i=1,2,…,20)对应的信号强度RSSIi的值,如表1所示。
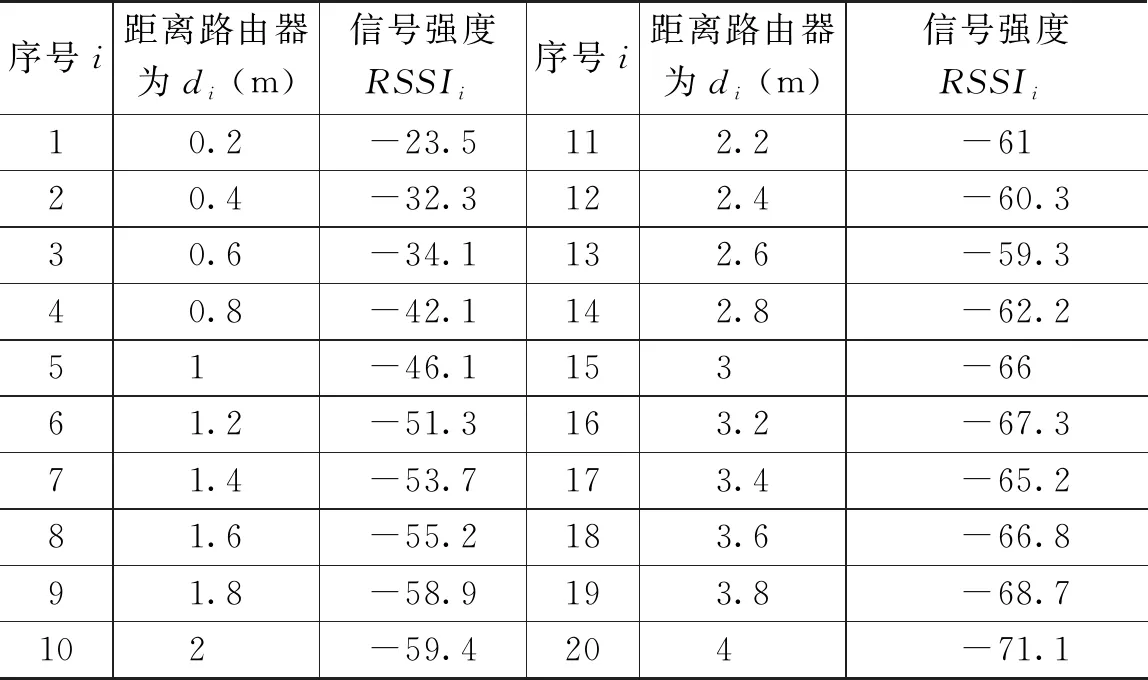
表1 实验数据
2.2 数据拟合测距
运用上述数据进行拟合得参数
A=-47.03,n=3.71,
将A= - 47.03,n=3.71代入(1)式得如下模型
RSSI=-47.03-37.1lgd,
将上式进行反解得数据拟合测距模型
(3)
代入表1中的RSSIi数据的模型(3)的预测值
并计算相对误差
计算结果见表2的第3,5列。
2.3 BP神经网络测距
将表1的数据信号强度RSSIi作为输入,距离di的值作为输出,选取两个隐含层,细胞元的个数分别为4,7进行训练。最大训练次数5 000次,网络的学习速率0.05,连接函数分别为'purelin', 'logsig'。训练结果,如图2所示。

图2 BP神经网络训练结果
通过仿真,并进行反归一化得BP神经网络训练的仿真值RSSI2i′,再计算相对误差
计算结果见表2的第4,6列。
2.4 结果分析
为比较数据拟合测距与BP神经网络测距效果,我们将两种方法的预测值及相对误差进行比较研究,计算结果,如表2所示。

表2 数据拟合与BP神经网络测距对比
由表2可以看出,数据拟合测距的最小相对误差为 0.35%,最大相对误差为16.36% ,平均相对误差为9.9%;BP神经网络测距的最小相对误差为0.03%,最大误差为16.06%,平均相对误差为3.89%。同时由图 3测距对比图及图4测距误差对比图可以看出,BP神经网络测距算法比数据拟合测距更精确。

图3 测距对比
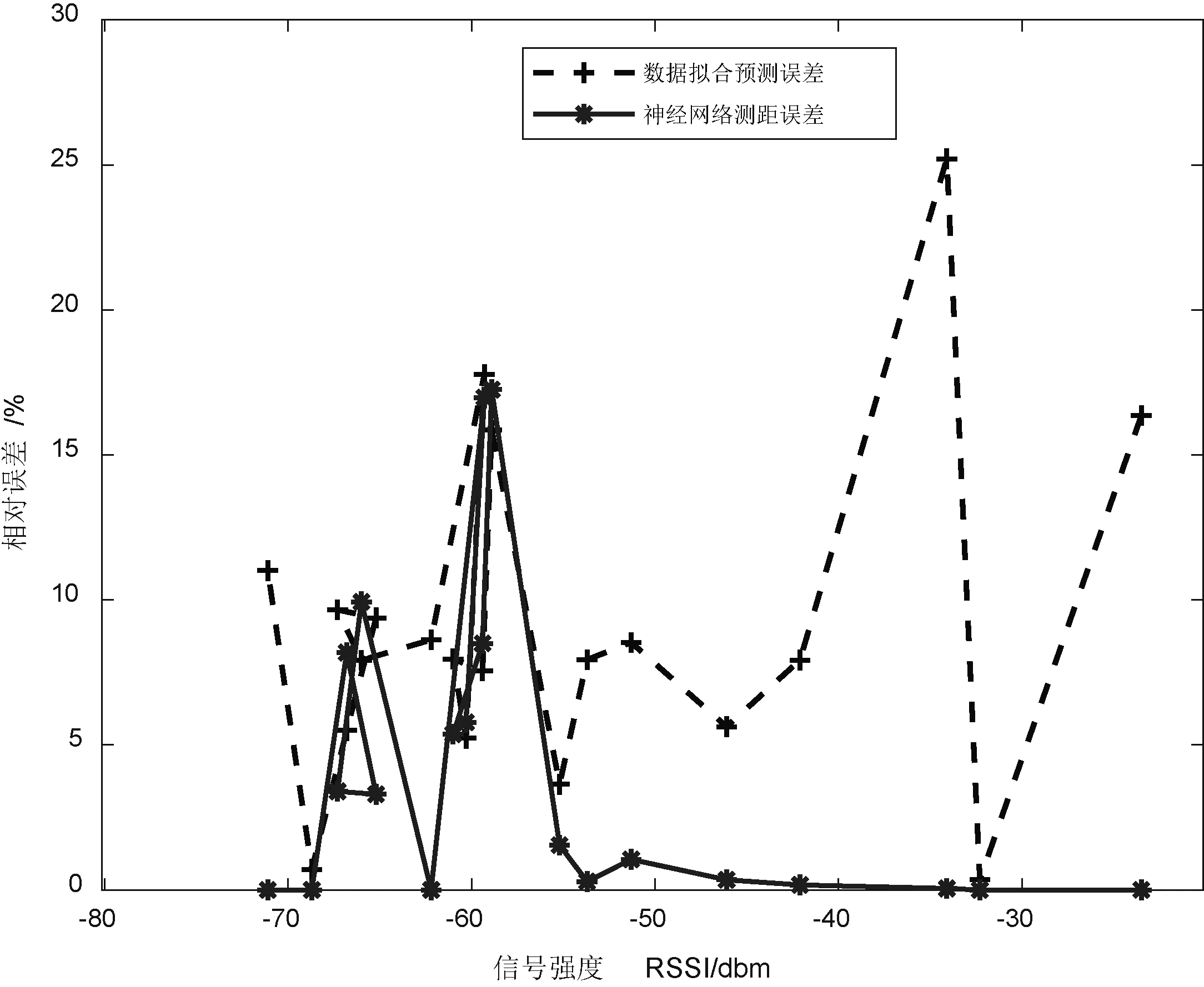
图4 测距误差对比
3 算法实现
由于BP神经网络测距的更精确,本文将以Matlab2020b为平台,实现测距的程序化、自动化。其代码如下:
%% 测量数据
d0=0.2:0.2:4;
RSSI0=[-23.5 -32.3 -34.1 -42.1 -46.1 -51.3 -53.7 -55.2... -58.9 -59.4 -61 -60.3 -59.3 -62.2 -66 -67.3 -65.2 ...
-66.8 -68.7 -71.1];
%目标输入输出
p = RSSI0;t = d0;
[pn, inputStr] = mapminmax(p);[tn, outputStr] = mapminmax(t);
%对训练集中的输入数据矩阵和目标数据矩阵进行归一化处理
[pn, inputStr] = mapminmax(p);
[tn, outputStr] = mapminmax(t);
%建立 BP 神经网络
net = newff(pn, tn, [4,7], {'purelin', 'logsig'})
%每 10 轮回显示一次结果
net.trainParam.show = 10;
%最大训练次数
net.trainParam.epochs = 5000;
%网络的学习速率
net.trainParam.lr = 0.05;
%训练网络所要达到的目标误差
net.trainParam.goal =5*10^-4;
%开始训练网络
net = train(net, pn, tn)
%使用训练好的网络,基于训练集的数据对 BP 网络进行仿真得到网络输出结果
answer = sim(net,pn);
%反归一化输出测距结果
d2= mapminmax('reverse', answer, outputStr)
%绘制测试样本神经网络输出和实际样本输出的对比图(figure(1))
figure(1);
plot(RSSI0,d0, '+',RSSI0, d2, 'r','linewidth',1.5);
ylabel('距离d/m')
xlabel('信号强度RSSI/dbm')
4 结语
本文利用数据拟合,求出测距模型参数A=-47.03,n=3.71,实现数据拟合测距;建立BP神经网络,将信号强度值作为输入,距离作为输出,进行有效训练。对两种测距方法进行比较研究,通过误差分析,BP神经网络测距精确度更高。本设计以Matlab2020b为平台,实现测距的程序化、自动化。
