基于SSA-DBN的光伏阵列故障诊断方法
2022-08-23郭欢欢代金超
姜 萍,郭欢欢,代金超
(河北大学电子信息工程学院,河北保定 071000)
近年来,随着光伏发电技术的飞速发展,光伏阵列也逐渐规模化。然而光伏阵列设施往往建立在环境比较恶劣的条件下,难以避免地会发生一些故障,如开路、短路、局部阴影问题、老化问题等。因此如何有效地对光伏组件的故障进行检测,使光伏阵列运行得更加稳定、有效变得尤为重要[1-3]。
目前常用的光伏故障诊断方法主要包括;红外图像识别技术[4]、单刀多掷开关结合传感器[5]、支持向量机[6]、人工神经网络[7]、主成分分析法[8]等。随着人工智能的快速发展,许多专家和学者把目光投向了模糊聚类、相关向量机,并且在光伏诊断方法中机器学习、模糊神经网络等方法中取得了很好的效果,然而这些方法局限于小数据集的学习和训练,处理数据集特征能力不足,容易陷入局部最优、提取特征困难等问题。
在智能诊断算法当中,深度学习网络凭借其深度挖掘样本的特征能力,分层处理样本的特征信息等优点,已经广泛应用于人脸识别[9]、功率预测[10]等领域,近几年来也渐渐应用于各种模型故障的诊断当中。
然而在深度信念网络训练中依然会遇到诸多的问题,如DBN 网络在训练和学习时其权值、偏置是随机产生的,网络参数会陷入局部最优。文献[11]采用改进粒子群算法对深度信念网络的权值进行优化,以此提高模型预测的能力;文献[12]采用混沌免疫算法对DBN 网络参数进行优化,并且引入了可变选择算子,提高了网络寻优的收敛速度;文献[13]提出利用布谷鸟搜索算法的全局寻优能力优化DBN 网络的初始权值,解决了原始DBN 网络的权值随机初始化问题。尽管这些智能算法对深度信念网络权重进行了优化,却缺乏对网络神经元的偏置优化。为了提高DBN 网络的有效性和稳定性,需要同时对网络的权重和偏置进行优化编码。
本文采用一种新型的智能算法麻雀搜索算法来提高DBN 网络的容错性,麻雀搜索算法在寻优精度、收敛性、稳定性和鲁棒性等方面优于其他智能算法[14],可以有效地避免陷入局部最优。将麻雀搜索算法用于深度信念网络中,对网络权值和偏置的优化起到了至关重要的作用,也提高了光伏阵列故障诊断的识别精度。
1 深度信念网络
1.1 DBN 模型
DBN 模型[15]是一种概率生成模型,由多个限制玻尔兹曼机堆叠而形成的网络模型,既可以完成有监督的数据分类和预测,也可以实现无监督的数据特征提取。本文利用DBN 网络对光伏阵列采集的故障数据集进行特征提取以及数据分类,DBN 故障诊断模型如图1 所示,输入端为标况下光伏组件典型四种参数,分别是开路电压Uoc、短路电流Isc、最大功率点电压Um、最大功率点电流Im,输出层分别为正常、短路、开路、老化异常、局部阴影五种状态,经历隐藏层对数据的处理和模型的自学习过程后,最终由分类器实现数据的分类。

图1 DBN 故障诊断模型
1.2 受限玻尔兹曼机
受限玻尔兹曼机(restricted Boltzmann machine,RBM)由两层神经网络构成:第一层是可见层,第二层是隐藏层。各层之间权值进行无向全联系,可用于对仿真模型计数统计。确定第一层状态后,第二层神经元不会受其他神经元影响,训练可分为三部分:正向传播、反向传播、比较。RBM 结构图如图2 所示。

图2 RBM 结构图
[Y1,Y2……Ym]为第一层神经元,m为可见层神经元数量,Yi是可见层神经元状态;[X1,X2,X3……Xn]第二层神经元,n表示隐藏层神经元数量,Xj是隐藏层神经元的状态,可见层和隐藏层用二进制数0 和1 来分别表示神经元的断开和接通状态,可见层和隐藏层之间的能量函数可表示为式(1):

式中:Bi和Yi为第一层可见层偏置值和神经元;Cj和Xj为第二层隐藏层偏置值和神经元;Bi、Cj为基于二进制状态的数值;Wij为各层神经单元的连接权值,可得到能量函数(Y,X)隐藏向量联合概率分布为式(2):
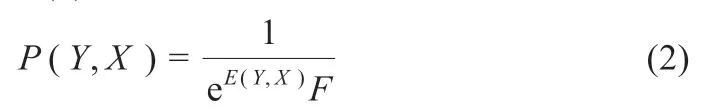
式中:函数F是通过所有可能的可见层和隐藏层的向量求和而产生的,如式(3):

随着可见层状态确定,隐藏层的激活概率也能计算,得到第j个神经元的激活条件概率为式(4):

本文选用ReLU 函数,通过ReLU 函数求得激活概率值,相比于sigmoid 函数计算速度会更快,表达式为式(5):
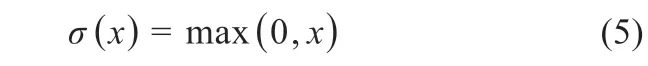
式中:σ(x)为激活函数。
一旦隐藏层神经元状态确定后,随机选择二进制数0 或1更新可见层的状态,可见层中第i个神经元激活的条件概率可表示为式(6):
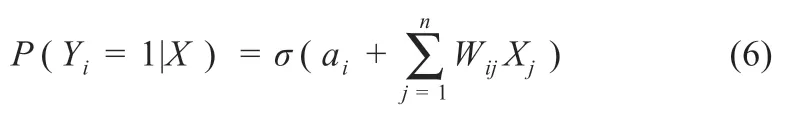
未被激活的概率则可表示为式(7):

1.3 深度信念网络训练步骤
(1)预训练阶段:采用无监督贪婪学习算法对RBM 网络进行逐层训练,将底层的原始数据转化为更抽象的特性信息以初始化RBM 的参数,将隐藏层输出作为可见层输入,保证训练过程中参数避免陷入局部最优解,提高参数在训练过程中的抗振荡性能;
(2)微调阶段:预训练完成后,基本完成模型的建立,但是依然只能确定每个RBM 达到最优状态,无法确保堆叠后的网络参数最优化,还需要把分类器输出的参数矩阵进行微调,确保初始信息可以被放大,在此过程中采用BP 神经网络从上到下微调并监督深度信念网络的参数让整个网络由局部最优状态转变成全局最优,整体结构图如图3 所示。
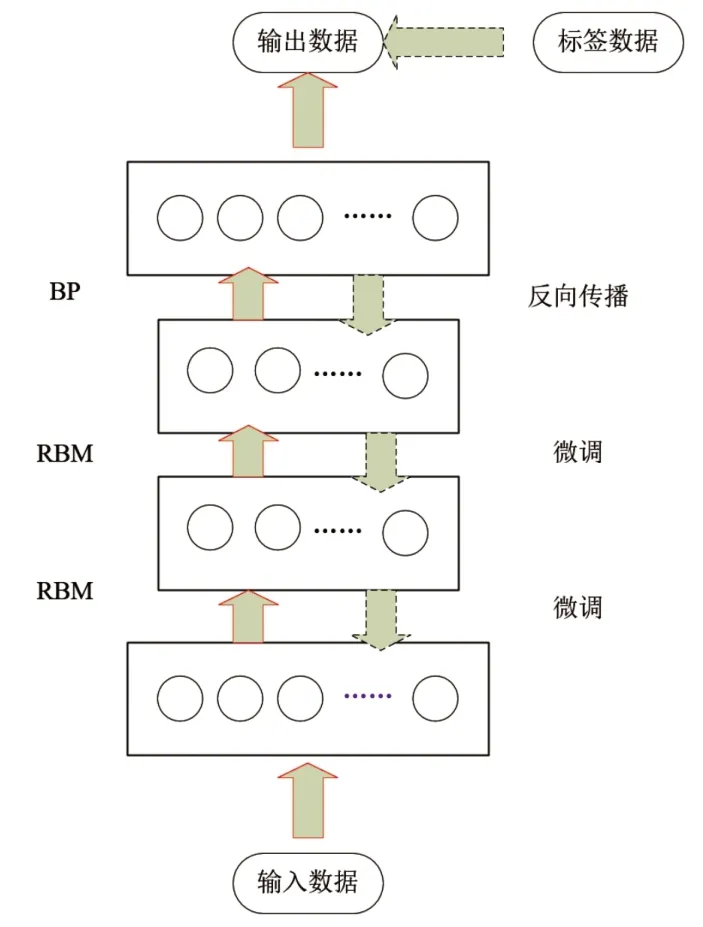
图3 DBN 网络结构图
2 基于麻雀搜索算法的DBN 网络
2.1 麻雀搜索算法
对于DBN 网络在训练和学习过程中容易陷入局部最优解且求解速度缓慢等问题,采用近年来提出的麻雀搜索算法(SSA)来优化DBN 网络的权值和偏置,以提高DBN 网络的识别精度和收敛速度。
SSA 算法是一种新型元启发式算法。在麻雀的觅食行为中,分为发现者和加入者两个角色,并加入观察报警机制。发现者负责种群的搜索和觅食,为种群提供方向;新加入者可以跟随发现者,获取更佳的适应值。当种群发生危险时可以进行反向捕食行为,根据麻雀的这些觅食行为,得到发现位置更新公式(8):
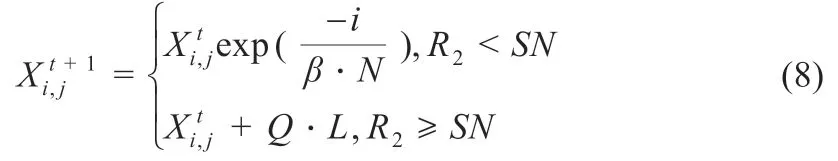
式中:t为种群目前迭代次数;N为最大迭代次数;β 取值为(0,1]之间的随机数为第i个麻雀第j维的位置;R2为[0,1]的随机数,表示种群的预警值;ST为[0.5,1]的随机数,代表种群的安全值。R2

式中:Xworst为目前全局最差的位置;A矩阵中的元素赋值-1 或1。当i>n/2 时,代表最差的追随者需要前往更远的区域获取更多的能量源。出现危险时,麻雀的反捕食行为公式为(10):

式中:α参数用来控制迭代步长,是一个服从正态分布的随机数;Xbest为种群最优位置;K为[-1,1]之间的随机数;fg为最佳适应度值;fw为最差适应度值。
2.2 SSA 优化深度信念网络
SSA-DBN 流程设计为:
(1)初始化种群数量:对DBN 网络可见层权值和隐藏层进行编码操作,设置觅食种群中发现者和加入者个体的比例;
(2)选择适应度函数:在对DBN 网络进行训练时,可以采取合适的适应度函数对动量参数进行优化,可减小参数训练过程中的误差,具体函数为式(11):
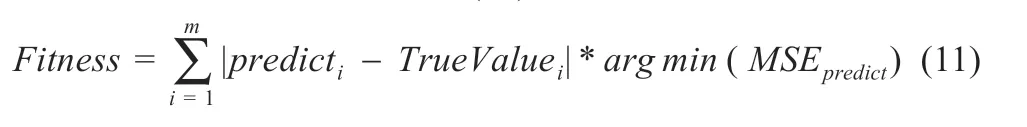
(3)觅食:在m维空间进行觅食搜索,其中第j只麻雀最先找到食物的概率为式(12):

式中:Fitnessl为第l只麻雀的适应度值,l取值范围为[1,n]。
(4)种群飞行路线:种群根据飞行过程中食物的位置,选择合适的飞行路线,对觅食路线中的惯性权重Z进行优化,可表示为式(13):
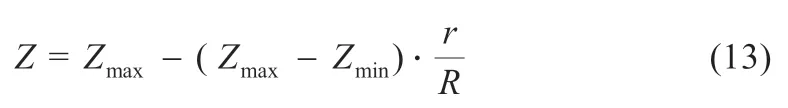
式中:R为最大迭代次数;Zmax和Zmin分别为权重的最大和最小值;r为当前的迭代次数。
(5)觅食位置调整:种群在靠近食物时,发现者以新加入者目前所在位置附近能否发现更好的食物为依据,以此来不断调整飞行速度、方向和位置,可表示为式(14)和(15):
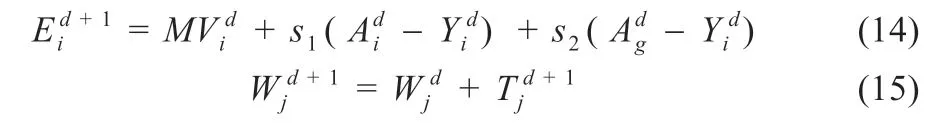
SSA 优化后DBN 网络的权值和偏置根据原始网络结构自行调节,对各参数进行微调如图4 所示,最终构建起应用于光伏故障检测的优化SSA-DBN 模型。
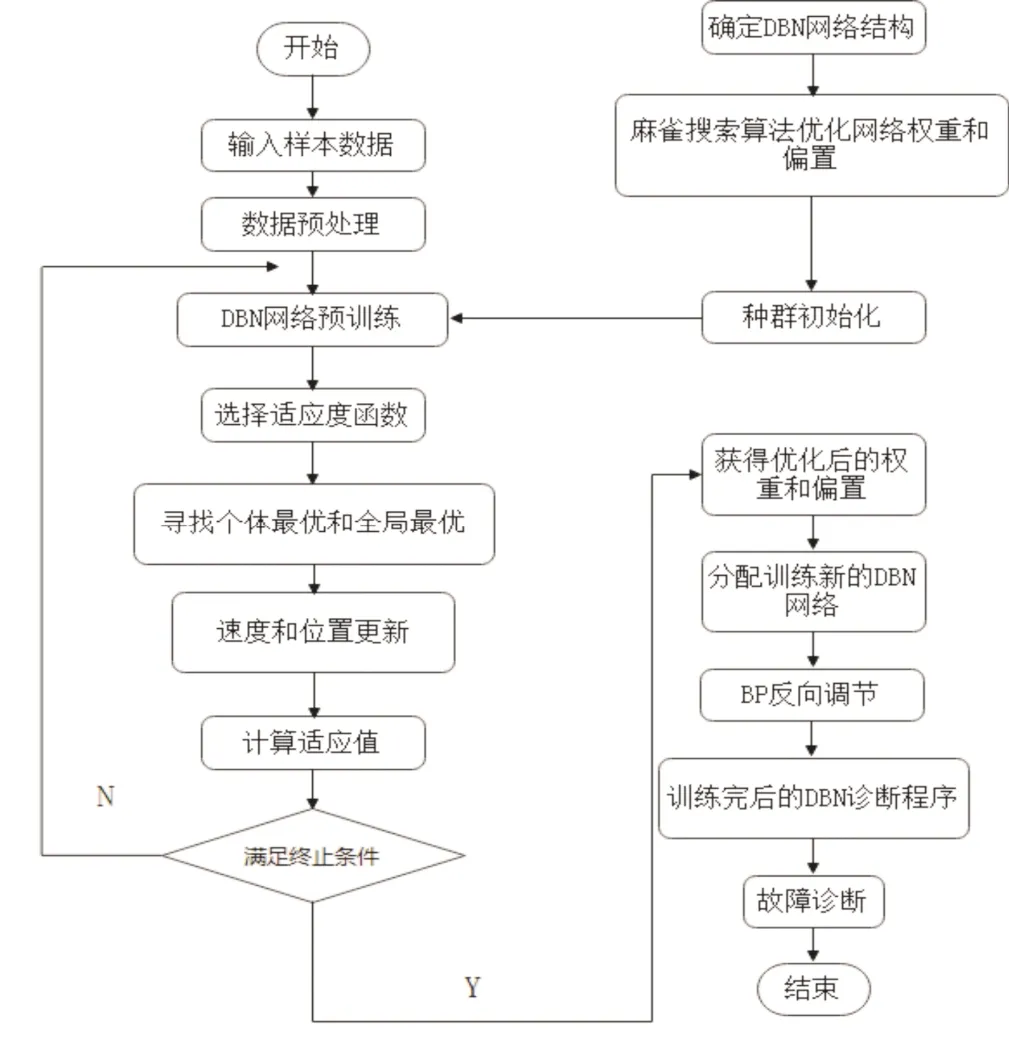
图4 SSA优化DBN 网络结构图
3 光伏阵列故障诊断模型
3.1 确定网络输入输出节点
把麻雀搜索算法优化DBN 网络模型应用到光伏组件的故障诊断模型当中,以光伏组件的四个特征参数作为优化网络的输入层,以最常见的五种光伏运行状态为输出层,对不同类型的故障进行输出节点编码如表1 所示。

表1 输出编码及运行状态
3.2 获取样本数据集
本文通过MATLAB 与PSIM 联合仿真来模拟各类光伏故障运行状态,首先在PSIM 软件中对光伏组件进行参数设置,然后模拟了四种故障类型如表2 所示。

表2 故障类型及对应参数值
在PSIM 中设置接口模块与Simulink 通讯,改变PSIM 内部电气参数,以辐照度、温度为输入,输出为组串一、二的电压和电流值及相应故障标签如图5 所示。Simulink 模拟四种故障的过程:先采集光伏电站中光伏组件的辐照度、温度;再设置各类故障参数,改变故障类型实现模拟;加入示波器观察输入变化过程;最终得到10 万组正常和故障数据集,联合仿真整体结构见图6。
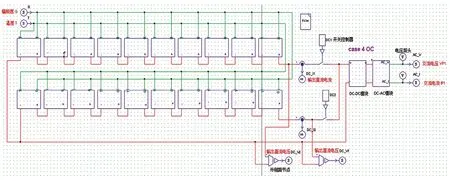
图5 PSIM整体故障模拟电路图
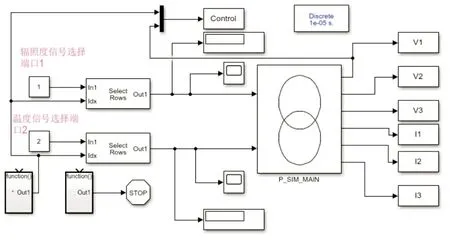
图6 联合仿真整体结构图
3.3 仿真结果分析
根据仿真平台实验,可以获取标况下(G=1 000 W/m2,t=25 ℃)各个故障数据集,得到光伏阵列四个参数(Uoc、Isc、Um、Im)的典型值,以及在5 种运行状态下的P-U和I-U曲线,如图7 和图8 所示。
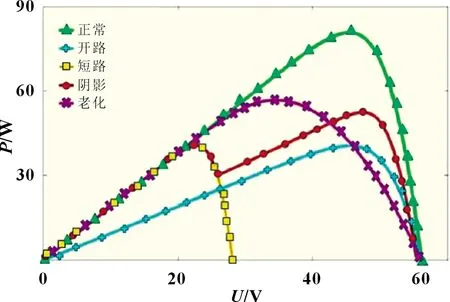
图7 五种工作状态下的P-U 曲线
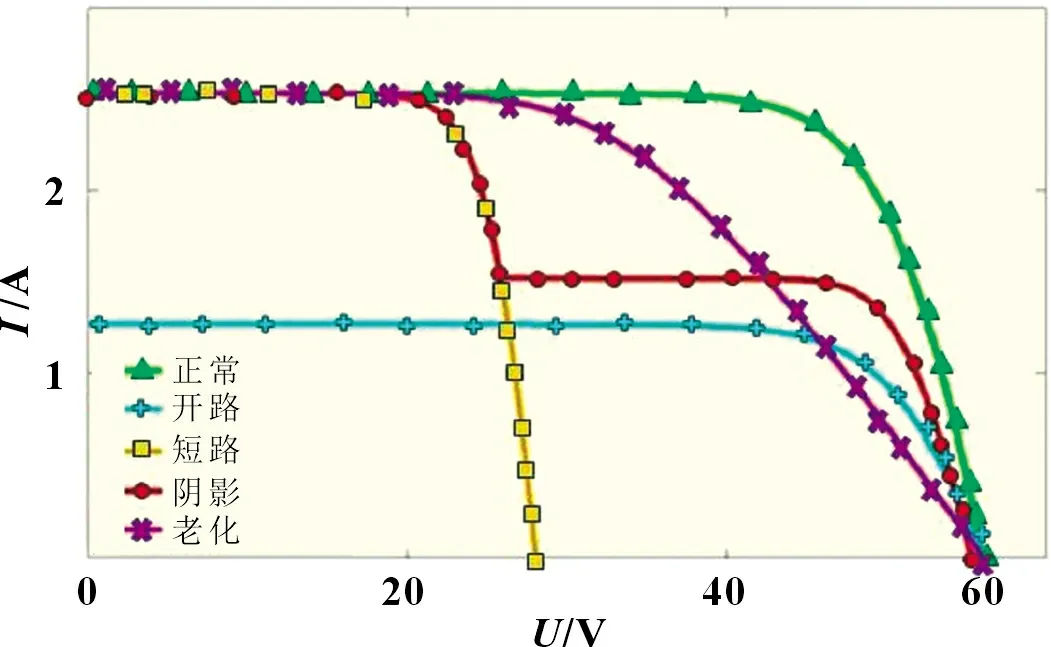
图8 五种工作状态下的I-U 曲线
3.4 样本数据集的归一化
故障数据参数在取值范围方面存在差异性,具有不同的度量尺度,因此在实验过程中其所占权值比例也存在差异,所以需要把原始数据进行归一化处理,可表示为式(16):

式中:M为原始数据为数据集参数量;Mσ为此特征的标准差;M*为归一化处理后数据。不同量纲的参数进行比较,可提高最优解的速度和精度,加快求出最优解。
4 实验验证
为减少训练时间,从所得10 万组故障数据集中随机选取20 000 组数据进行训练,随机选取500 组数据用来检验模型的准确性和有效性,具体设置如表3 所示。进行15 次实验,以减少偶然误差,记录训练模型所花费的时间。
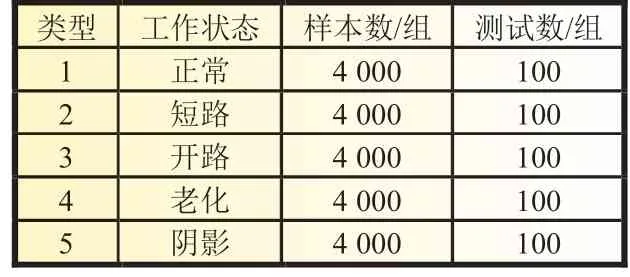
表3 数据集设置
DBN 故障诊断模型参数设置:输入输出神经元个数分别为4 和5;迭代次数100;动量参量取0.4~0.8 之间,取中间值0.6;学习率取0.1;隐藏层网络层数采取20-30-50-30-20 的中凸形最佳结构。
4.1 SSA-DBN 特征分析
为充分表现SSA-DBN 算法的优势,采用重构误差对其进行评估,重构误差是一种最大似然估计方法,能够反映受限玻尔兹曼机的学习效果,也是对模型进行评价的重要指标,其定义如式(17)所示:
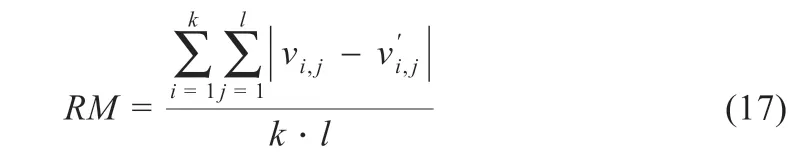
式中:k为样本个数;l为输入维数;vi,j为原始数据为受限玻尔兹曼机进行一次采样后得到的重构数据,三种算法的重构误差如图9 所示。

图9 重构误差曲线
根据图9 分析可知,SSA-DBN 的重构误差明显低于DCNN 模型和传统DBN 网络;DCNN 模型的初始值和稳定时的重构误差最高,迭代130 步后趋于稳定,但仍有波动,幅度也较大;而原始DBN 的初始误差要比DCNN 略低,经历90 个迭代步数后达到稳定;相比这两个算法来说,改进后的DBN算法初始值为0.1 左右,起始值也最低,只经历10 次步数已达到稳定。证明了SSA 在DBN 参数优化方面取得了显著的效果,不仅提高了收敛速度,也降低了重构误差。
4.2 结果对比分析
将DCNN 算法、DBN 算法、SSA-DBN 算法进行对比分析,见表4。
从表4 数据对比分析可知,在这三种算法中DCNN 算法各类型故障准确率均值只有86.93%,在阴影故障方面表现稍好;其次是DBN 算法平均准确率达到92.1%,各个故障类型均达到了90%以上,表现良好;最后是SSA-DBN 算法,光伏组件五种工作状态的平均诊断准确率达到97.71%,与原始DBN 算法相比提高5.61%,实验证明SSA-DBN 在故障诊断过程中达到了较好的全局寻优效果。
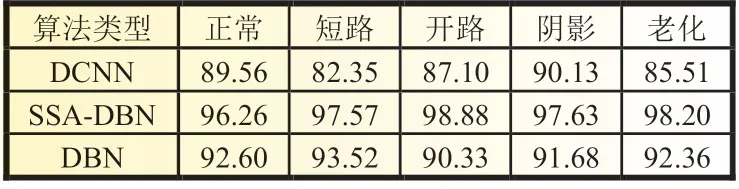
表4 不同算法诊断准确率 %
5 结论
本文提出了一种麻雀搜索算法优化DBN 网络的光伏阵列故障诊断方法,通过仿真实验与传统的深度学习网络相比得出以下结论:
(1)通过SSA 算法对DBN 网络的权值和偏置进行优化,避免模型训练过程中由于迭代更新而影响训练速度,同时也增强了对光伏故障数据集特征提取和分类的能力。
(2)优化后的DBN 网络重构误差明显低于传统DBN 网络和深度卷积神经网络,其故障诊断准确率明显高于另外两种网络,SSA-DBN 模型不仅提高了收敛速度,也提高了光伏故障诊断精度。
