概率模型在图像分类方面的应用
2022-08-23北方工业大学信息学院童立靖杨帆
北方工业大学信息学院 童立靖 杨帆
随着互联网、多媒体技术的不断发展以及图像数据的迅速增长,如何对大量的图像数据进行有效的图像分类已经成为目前图像处理技术研究的热点问题。对提取的图像信息特征结合概率模型求解图像分类的问题,能够有效提高图像分类的效率与精度。本文主要介绍了极大似然估计、最大期望算法和变分推断三种求解方法,并总结归纳了基于这几种概率模型的图像分类方法的研究现状,以及这些方法的优缺点,最后总结了有待深入研究的难点问题,并对基于随机变分推理的图像分类方法进行了展望。
在数据规模不断增大、数据类型不断增多的情况下,能够快速、高效的处理信息是计算机急需具备的能力,这也是我们技术研究的主要方向。目前在图像处理领域主要面临的问题是由两方面矛盾所产生的。一方面是图像信息数据大量涌现,其中包括含有图像、音频等多种数据;另一方面是计算机缺乏对快速增长的数据进行处理的能力。图像分类技术正是解决这一问题的有效途径,它可以自动构建与人类认知相一致的图像语义信息,从而对图像信息进行自动、高效的处理。图像分类已经成为图像识别的关键技术之一,因此在海量数据的背景下研究图像分类方法具有极其重要的研究意义和应用价值。其中,由于结合概率模型创建的分类器具有效率高、时间短等优势,所以该方法得到了广泛的应用。同时将概率模型结合深度学习的知识进行数据处理,效果更加突出。然而求解概率模型参数的方法在不断发展,贝叶斯理论的主要目的是求解概率混合模型的后验分布,并通过求解后验分布估计出模型的参数。目前应用较为广泛的是通过概率模型求解图像分类领域中的问题。同时概率模型的灵活性使得其在处理图像分类中具有很大优势,所以值得我们去研究和讨论。
进行参数估计的方法主要分为两个派别,分别是频率派和贝叶斯派。频率派主要包括最大期望算法(Expectation-Maximization Algorithm,EM)和极大似然估计法(Maximum Likelihood Estimate,MLE);贝叶斯派主要包括马尔科夫蒙特卡洛(Markov Chain Monte Carlo,MCMC)、变分推断(Variational Inference,VI)和随机变分推断(SVI),以上方法在计算机视觉、图像处理、语音识别、生物特征提取与识别、文本分类等很多领域都有应用。
近年来不少学者在采用概率论的知识建立模型进而完成图像分类的目标,文章从四大部分进行介绍:(1)介绍极大似然估计法、最大期望算法和变分推断;(2)对于近些年采用概率知识进行图像分类的文献进行综述;(3)根据上述综述介绍各方法的优点和弊端;(4)展望和总结。
1 方法介绍
1.1 极大似然估计
极大似然估计法又称最大似然估计或最大概似估计,该方法首先是在1821年由德国数学家高斯提出。通过多次对于概率函数中的参数进行求导得到最大解,进而求解相应的参数θ
。极大似然的思想是通过最大化似然函数求解参数。极大似然估计法认为模型中的参数都是固定的未知参数,通过最大化似然函数求解参数。假设取一组总数为N的样本,其中他们的观测值分别为X
=(x
,x
,……,x
),θ
为参数,所以N个样本的概率如式(1)所示: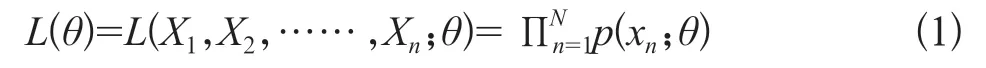
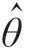
1.2 最大期望算法
EM算法是由美国数学家Arth ur Dempster等在1977年提出来的,并给出了计算步骤和总结。EM算法是把迭代的思想和极大似然估计方法进行结合的一种改进算法,适用于含有隐变量的概率模型的求解。在求解过程中运用到了Jensen不等式。
Jensen不等式的建立过程是:
存在一个变量X,假设h
(x
)是一个凸函数,那要满足如式(2)所示:
q
(z
),可以将(1)式改写为如式(3)所示: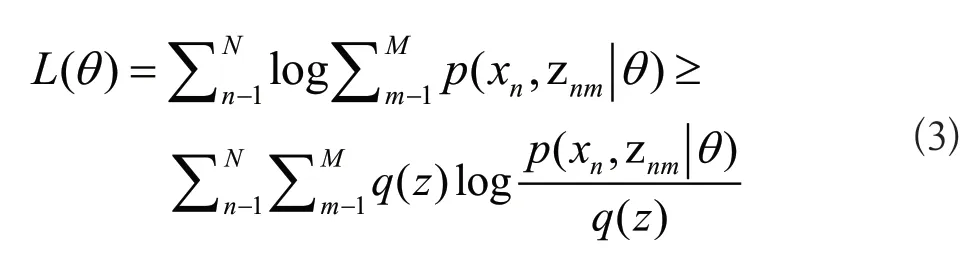
q
(z
)=p
(z
|x
)。EM算法的过程是:
(1)初始化参数θ
;(2)E-Step:根据参数θ
,计算得到q
(z
)=p
(z
|x
,θ
);M-Step:根据q
(z
)=p
(z
|x
,θ
),得到它的似然函数L
(θ
)并最大化,得到新的参数θ
';其中Z
为隐变量Z
=(z
,z
,……,z
)。当数据属于该模型分量时Z
=1;反之,如果Z
=0,重复迭代第2步,直到收敛。1.3 变分推断
变分推断的核心思想是通过固定其中一项,不断进行迭代,直到收敛来求解参数。
贝叶斯派是求解真正的后验分布,贝叶斯求解后验分布的公式如式(4)所示:
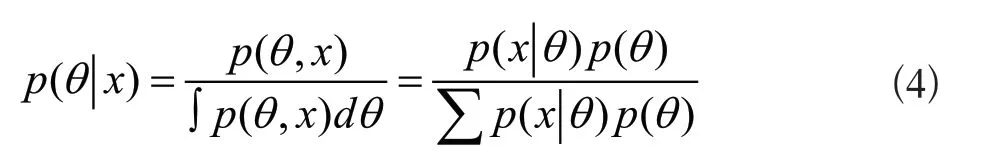
q
(z
)来近似真正的后验分布,使得KL
达到最小,满足如式(5)所示:
KL
(q
||p
)=E
[lnq
(z
)]-E
[lnp
(z
|x
)],是关于q
(z
)和后验概率两者期望的差值。由于存在后验分布,KL
散度难以直接求出,如图1所示中描述有关KL散度和证据下界ELBO的关系,可以将问题转变为求解证据下界ELBO,整理得到ELBO如式(6)所示: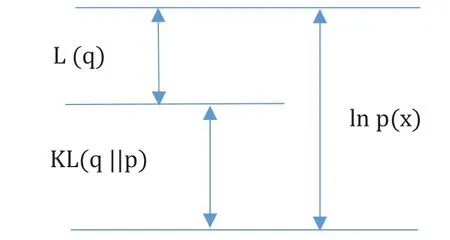
图1 变分原理关系图Fig.1 Variational principle diagram
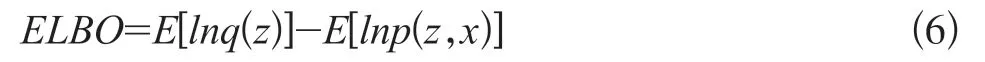
变分推理的目标函数如式(7)所示:

lnp
(x
)是固定的,其中L
(q
)为证据下界ELBO
,这样就将最小化KL
散度转化为最大化证据下界。采用平均场理论(Mean-field Theory)可以得到如式(8)所示:
将(8)代入(6),两式相结合化简后可以得到变分推断的通式如式(9)所示:
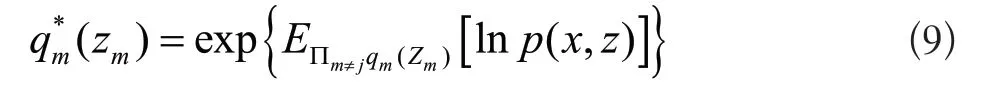
q
(z
),不断更新方程(9),直到ELBO
收敛,达到最优值。2 基于各方法的图像应用综述
2.1 基于极大似然估计法的图像分类应用
极大似然估计法作为一种传统的估计方法,具有广泛的适用性。2000年Lina Zhuang等人中使用极大似然分类器,在全球热带雨林监测到的图像数据中验证方法的有效性。2016年Muhammad Ali等采用不同于其他多元分布方法的极大似然估计法进行分类,展示了一种新的参数化分类建模方法。2019年Jiangtao Peng等介绍了建立一个基于最大似然估计法的JSR模型来提高联合稀疏表示方法的鲁棒性,并且能够在大噪音的情况下展现出很好的效果。
2.2 基于最大期望算法的图像分类应用
2007年张春燕等采用t-混合模型的EM迭代算法估计模型中的未知参数,计算形状类别的后验分布,实验结果表明按照后验概率分类的准确性较高,并在MEPG-7,SETB标准库中选取蝙蝠和花瓣的图像,有很好的实验效果。2013年Lina Zhuang等中提出一种改进的EM,能够得到比传统EM在少量训练样本下更好的分类结果,更高的准确性,并在图像数据集上得以验证。2015年Martín Hurtado等人提出一种基于期望最大化(EM)算法的极化SAR图像分类方法,该方法能够将类的数量识别为初始信息,提高结果的准确性。
2.3 基于变分推断的图像分类应用
2018年Yuping Lai提出一种IDMM的变分推理框架和传统的期望最大化算法相比,该方法能够较好的防止过拟合的现象,可以实现混合组分数量的自动确定和参数估计。2019年Z. Ma等中采用一种新的变分方法结合逆狄利克雷模型进行解析推导,避免贝叶斯估计法中容易出现的过拟合和欠拟合的问题,通过采用合成数据集验证在图像分类中能够有很好的表现效果。2021年Yuping Lai等采用可扩展的VI结合伽马模型构建分类器,在图像中应用后发现相比变分推断结合贝塔模型、狄利克雷模型及高斯混合模型在准确率方面都有所提升。
3 各方法的优缺点
极大似然估计法是一种较早的估计方法,能够广泛的应用到图像分类等各个领域,不足是似然估计方法对于初始值的设定比较敏感,易导致求解参数不是最优解,且在数据量较少的情况下不易收敛。另外使用极大似然方法求解混合模型时是不能简单求出的,这样就发展出了EM算法。
然而EM算法存在的一个缺陷是在收敛的过程中能够出现最优解,但是我们不视为局部最优解。此外,该方法也不适合应用到大规模的数据处理模型,由于处理数据过少,容易出现过拟合的问题。EM算法尚不能妥善解决模型选择的问题,因此产生了基于变分推断的图像分类方法。
变分推断方法和前两种频率派的方法相比有很大优势。一方面体现在对初始值的设定不敏感,不会影响概率模型求解的准确性和有效性;另一方面体现在将不能求解的散度问题转为求解证据下界ELBO的问题,有效避免了归一化常数不可求的困难。但该方法是基于平均场理论进行的变分推断,由于假设隐变量之间是相互独立的,所以不能够适用于一些特定模型的参数求解,而且变分推断的迭代思想使该方法在处理大规模数据时,时间效率上会有所减弱,不能够充分展现自己的优势。
4 总结与展望
通过第一节对各种算法的讲解以及第三节对各个方法优缺点的总结,可以看出频率派中最大期望算法和极大似然估计法有较大的局限性,所以在解决问题时这两种方法的使用相对较少。然而目前变分推断在图像领域的应用是比较广泛的,并且它能够较好的近似求解出后验概率。
变分推断的不断迭代思想使得它在数据规模巨大的情况下应用有所阻碍。因此急需继续研究一种新的方法来解决这一问题,随机变分方法是一种潜在的理想解决方案,但是目前对于随机变分推断的研究还较少,相关参考文献也比较匮乏,针对不同模型采用贝叶斯中的随机变分推断方法进行求解的结果还需要进一步研究。尚需尽早推算出使用随机变分方法结合不同模型求解后验分布的过程,并进行在图像分类领域的广泛实践,以尽快解决大量数据处理时的处理时间以及概率模型估计准确率问题。
