基于灰色模型的矿区地表沉降预测研究
2022-08-22张凯月
张凯月
(1.安徽理工大学空间信息与测绘工程学院,安徽 淮南 232001;2.安徽理工大学矿山采动灾害空天地协同监测与预警安徽普通高校重点实验室,安徽 淮南 232001;3.安徽理工大学矿区环境与灾害协同监测煤炭行业工程研究中心,安徽 淮南 232001)
0 引言
我国矿区众多,煤炭资源储量丰富,煤炭能源供应在国民经济发展中发挥着重大作用[1]。但大量采煤和过度采煤会造成地表沉陷,引发地质灾害。研究资料表明我国“三下”压煤总量的61%在建筑物地下[2],煤炭开采会损坏矿区建筑物,给矿区附近居民生活、区域经济发展和生态建设带来不便和阻碍。因此,研究矿区的地表沉降变形及沉降预测成为具有现实意义的研究内容。
基于非线性理论的预测方法是矿区开采沉降常用的预测方法之一[3]。灰色模型、神经网络模型、时间序列模型及多模型组合预测模型在目前沉降预测中的研究已经得到验证和应用[4-6]。其中灰色模型能利用小样本在离散化的数据中摸索出规律,进而进行预测和分析。宋海萍[7]、武君[8]、张庆斌等[9]通过实例论证了灰色Verhulst模型在矿区地表沉降中的预测精度高于GM(1,1)模型;杨俊凯等[10]、石晓宇等[11]利用D-InSAR与灰色模型结合,探究建立监测—预计一体化方法,结果表明灰色Verhulst模型预测精度较好。基于灰色模型种类多、适用情况不同的特点,本研究利用矿区沉降数据计算比较GM(1,1)模型、加权参数估计模型和灰色Verhulst模型在矿区沉降预测中的拟合精度和预测精度,探究三种模型在矿区沉降预测中的可行性和适用性。
1 灰色模型基本原理
1.1 GM(1,1)模型
灰色模型能对含有不确定因素的系统进行预测[12]。
①设非负等时间序列为
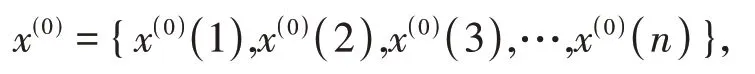
经过一次累加得到1-AGO序列为
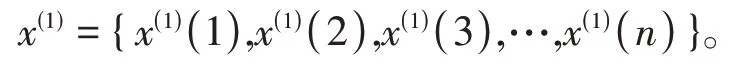
②灰色微分方程如式(1)所示。
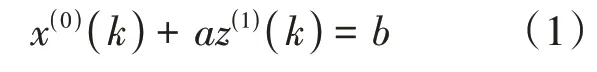
最小二乘法估计参数如式(2)所示。
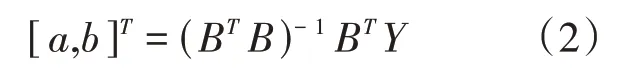
式中:a为发展系数,b为灰色作用量。
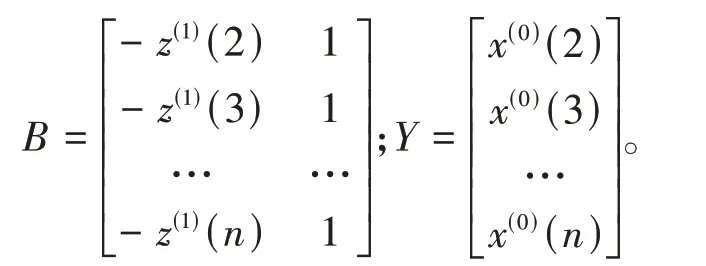
③白化方程如式(3)所示。
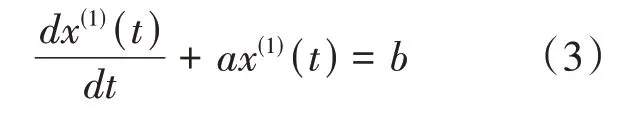
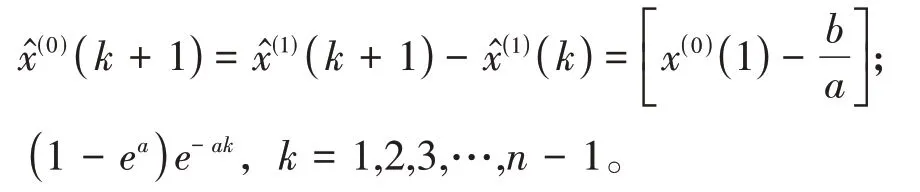
在进行灰色预测之前,需要对x(0)=进行级比检验以保证灰色预测的可行性。序列级比:λk=,k=1,2,3,…,n-1,级 比 结 果 在之间,可进行GM(1,1)预测,否则需对x(0)序列加一常数c进行平移变换满足级比要求。
1.2 加权参数估计模型
加权参数估计模型即加权最小二乘参数估计模型,何霞[13]阐明了灰色模型在最小二乘参数求解时会出现病态问题,而且GM(1,1)模型把误差平方和看成相同比重,两者均可能导致结果不准确,因此将灰色微分方程各部分误差平方和分配不同权重ωk(k=2,3,…n),使总误差和最小,以得到更适合的参数。且当时,取得的效果较好。
灰色微分方程如式(4)所示。
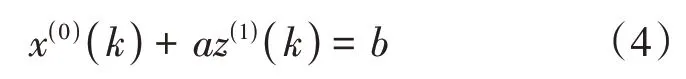
参数解算如式(5)所示。
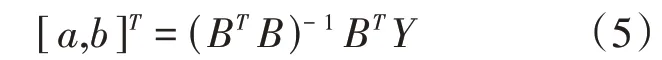
白化方程如式(6)所示。
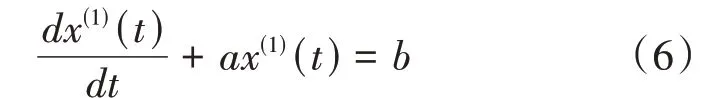
1.3 灰色Verhulst模型
①非负时间序列x(0)通过一次累加得到x(1)序列,背景值序列z(1)为紧邻均值序列。
②灰色微分方程如式(7)所示。
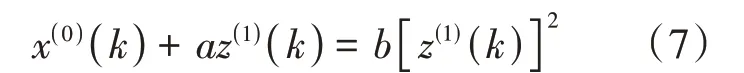
参数数列[a,b]T=(B T B)-1B T Y。
③白化方程如式(8)所示。
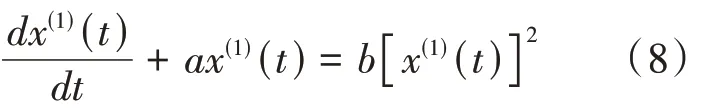
2 矿区沉降预测
2.1 矿区沉降数据
根据姜佃高等[14]等研究的矿区沉降数据,通过计算获取矿区观测点不同时间段的沉降量,利用三次样条插值法获得等时间段的沉降量,最后计算矿区累计沉降量。文中监测点A1与A2分别对应文献[14]中的B8点与B11点;监测数据从2012年6月开始至2012年11月16日结束,等时间间隔选取17 d,三次样条插值结果与累计沉降量如表1所示。
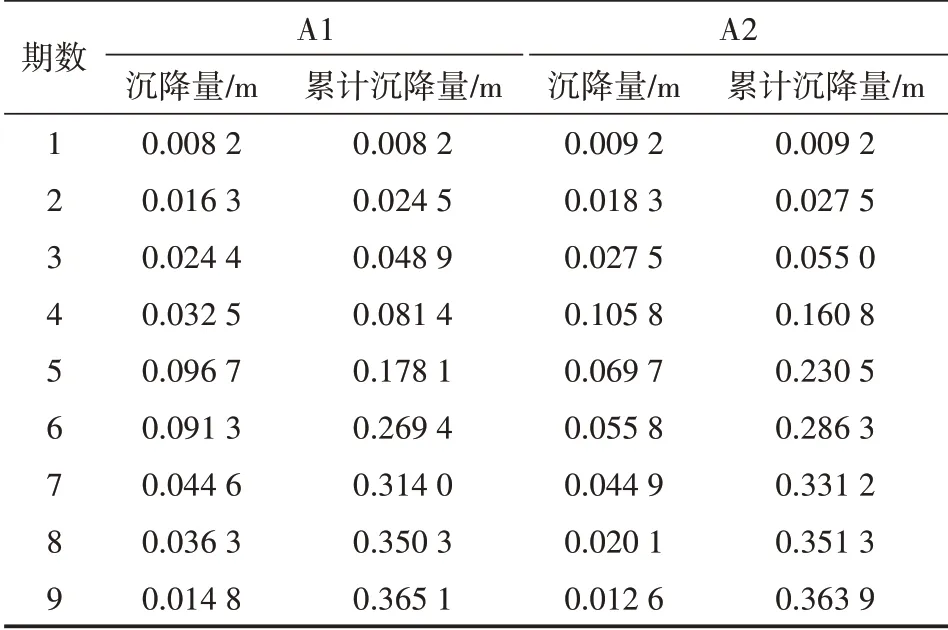
表1 观测点沉降数据
2.2 监测点沉降数据拟合与预测结果
运用3种预测模型,将前8期的数据进行数据拟合,对第9期的数据进行预测,得到数据拟合与预测结果,具体如图1、图2所示。
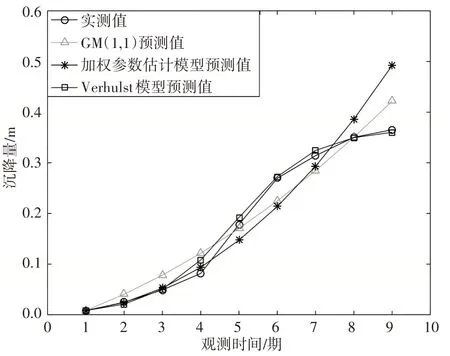
图1 A1点模型预测值与实测值对比图
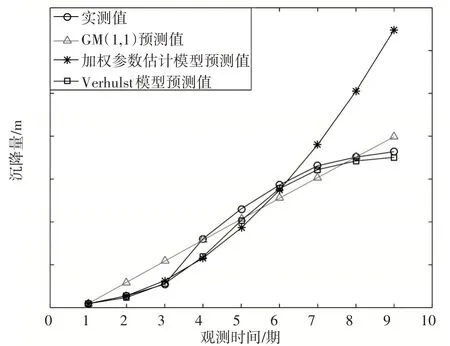
图2 A2点模型预测值与实测值对比图
2.3 精度检验
灰色模型精度检验包括数据拟合精度检验和预测精度检验。在拟合精度检验中后验差检验可以直接判断数据拟合的优劣,能直观判断出所选灰色模型的合理性,后验差比值C越小效果越好,误差概率P越大效果越好,C<0.35、P≥0.9时评价等级为1级,效果良好。
2.4 结果分析
①结合图1和表2可以看出A1点在总体上灰色Verhulst模型的拟合程度最佳,残差与相对误差最小,后验差检验效果最好,灰色关联性最强,拟合精度最高。GM(1,1)模型与最小二乘法加权参数估计模型拟合曲线均呈现上升趋势。
②从图2和表2来看,A2点总体上灰色Verhulst模型拟合效果最好,GM(1,1)模型次之,加权参数估计模型最差。1~3期加权参数估计模型拟合值与实测值误差最小,4~8期呈现类似指数式增长趋势,后验差检验等级为2级,属于合格级别。
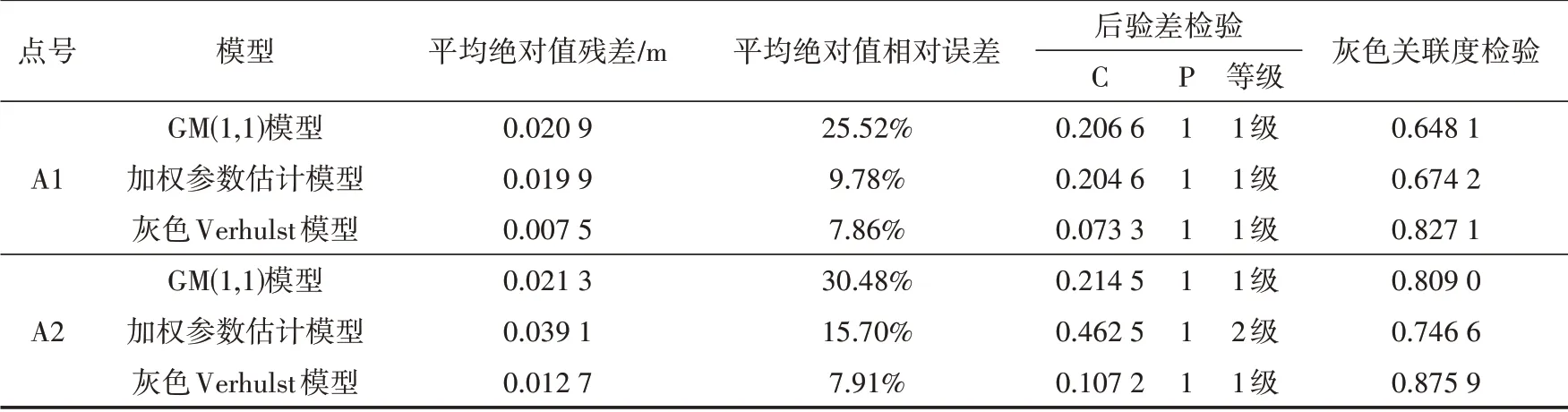
表2 前八期拟合精度检验
③从图1、图2和表3可知在A1点和A2点灰色Verhulst模型预测误差较小,加权参数估计模型误差较大,预测结果不能作为沉降预测参考。
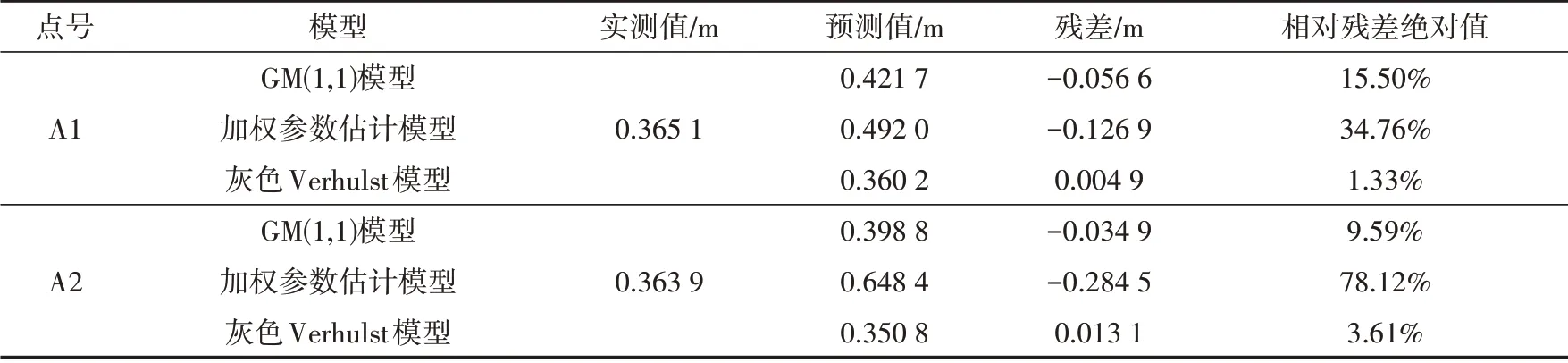
表3 第九期预测精度检验
④综合三种模型在A1、A2两点的拟合和预测结果,在前期沉降量较小时,加权参数估计模型与实际值最接近;当沉降量突然增大时,GM(1,1)模型在前期的拟合误差较大,加权参数估计模型在后期的拟合误差较大;后期沉降较小,加权参数估计模型预测偏离实际值太多。总体上灰色Verhulst模型拟合和预测情况最好,在矿区地表沉降预测中有良好的适用性。
3 结论
灰色Verhulst模型与实测值变化趋于一致,可应用于矿区地表沉降预测。GM(1,1)模型和加权参数估计模型不适用于沉降突然增大的情况,在此之前预测前期沉降效果会较好。矿区地表沉降影响因素众多,准确适时的沉降变形预测模型建立困难,在不考虑矿区地表以下影响因素的前提下,本研究中预测模型是可行适用的,精度较高。但要进行精准预测,需要考虑多方面因素;本研究中两个监测点并不能反映整个矿区沉降情况,后续研究会针对固定矿区,结合地表沉降影响因素,建立适合多点的矿区地表沉降预测模型。
