基于更新过程的多目标预防维修优化模型
2022-08-22杨荔贤
杨荔贤 余 俊
(阿坝师范学院数学学院,四川 阿坝 623000)
0 引言
维修模型经常使用的准则有3个:①维修费用、不能工作时间和维修时间最小化;②收入、利润和可用性最大化;③达到要求的可靠性和安全性水平。在开展维修活动时,可能基于一项或多项准则,使用单一的最优化准则建立起来的最优预防维修模型已无法满足现实需求,经常要根据不同的需求和资源限制来作出不同的决策。金燕生等[1]研究两个不同型部件的冷贮备系统的预防维修策略,在一般分布情况下利用补充变量法,求出系统首次故障前的平均时间和可靠度。程晓绚等[2]在几何过程理论的基础上,考虑工作时间受限的情况,提出单部件可修系统的最优更换策略。利用更新过程理论,计算出平均可用度、平均故障频度等,并给出系统的期望效益函数。高俏俏等[3]研究了一种可修系统的维修策略,当系统发生故障时,修理设备对其进行维修。利用更新过程和几何过程理论,可计算出系统长期运行后的单位时间内的期望费用。刘勤明等[4]以设备维修能力为约束条件,对库存缓冲区的多目标设备维修问题进行研究,在准更新过程的基础上,推导出设备的随机故障次数,以最大设备可用度和最小生产总成本为目标,构建出不完美预防维修模型,并利用粒子群算法得到更新周期内的库存量和预防维修周期两个决策变量的最优值。刘学娟[5]利用加速失效时间模型和基本随机回归系数模型,在考虑协变量的影响下,建立模型来分析设备的退化过程,针对退化过程设置两类更新阈值,一类是预防性维修更新阈值,另一类是故障更新阈值。运用更新回报定理,对两类更新周期内的单位时间期望维修费用进行建模,并对模型进行求解,可得设备的最优监测区间和最优预防性维修阈值。Paprocka[6]研究了具有截断正态分布故障率的预测维修策略,生产任务的优化是通过选取的参数估计方法来比较不同作业车间调度问题的描述扰动,基于最大似然估计法能更准确地预测调度问题。
综上所述,已有的大部分研究只是对维修策略中只有一个因素的单目标或由两个因素组成的多目标进行优化,并采用智能优化算法求解模型,且对考虑因素的数学表达式大部分没有推导过程。本研究利用更新极限定理,来推导出系统长期运行后单位时间期望维修费用、平均可靠度和稳态可用度,并运用极大模理想点法建立关于这三个目标和一个决策变量,即预防维修周期的多目标最优化模型,并结合算例给出求解过程。
1 更新报酬过程和更新极限定理
更新报酬过程[7]如下所示:{N(t),t≥0}是由非负随机变量X1,X2,……所产生的更新过程,假设Y n是第n个更新寿命X n中的报酬,且{(X n,Y n),n≥1}独立同分布。令为(0,t]时间内的总报酬,则称{Y(t),t≥0}为更新报酬过程。
更新极限定理[7]如式(1)所示。
若E Y n和EX n有限,则
更新极限定理说明了对长时间运行后求得的期望平均报酬等于一个周期内得到的期望报酬除以该周期的期望时间。
1.1 基本模型及假设
假设部件的寿命分布函数为Φ(t),当部件突发故障时对其进行小修,小修时间Y m服从一般分布,其均值为βm,部件经小修后,能够正常工作,且部件年龄不变。当累计工作时间达到部件的指定年龄T时,需要对部件进行预防维修,预防维修时间Y p,其服从均值为βp的一般分布,经过预防维修后的部件恢复初始状态,并能立即正常工作。故障小修每次费用为cm,预防维修每次费用为c p,(0,t]时间内的期望工作时间为M T,(0,t]时间内的期望维修费用为M C,(0,t]时间内的期望可靠度为M R;长期运行单位时间的期望维修费用为,t时刻的瞬时可用度为A(t),极限平均可用度为,稳态可用度为,失效率为γ(t)。在部件工作时间T内,发生故障的平均次数为m(T),可靠度函数为R(t),平均可靠度为。
假设小修时间、预防维修时间及部件寿命等因素相互独立。
再生点为部件的预防维修结束时刻,假设两个相邻的预防维修结束时刻之间的时间差是一个周期。很显然,各周期独立同分布,并形成一个更新过程,因此可运用更新极限定理来推导相关表达式[8]。本研究是要求最优的累计工作时间T(即预防维修周期T),使其能满足多项准则的最优化问题。部件的可能发展进程见图1。

图1 部件的可能发展进程
由上述分析可知,寿命的概率密度为Φ'()t,可得部件的失效率,见式(2)。
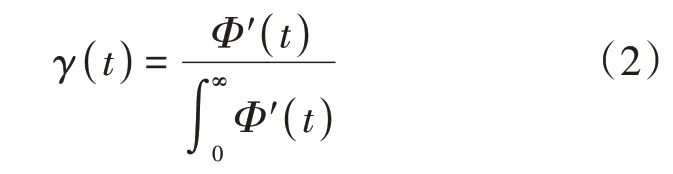
在部件工作时间T内,发生故障平均次数见式(3)。
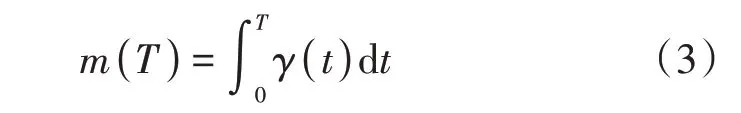
即周期长为=T+Y p+Y m·m(T),平均周期长为T+βp+βm·m(T)。
1.2 稳态可用度、长期运行单位时间的期望维修费用和平均可靠度的推导过程
若将工作时间看成其所在周期内的报酬,则(0,t]时间内的期望工作时间可看成(0,t]时间内的总报酬,更新极限定理见式(4)。


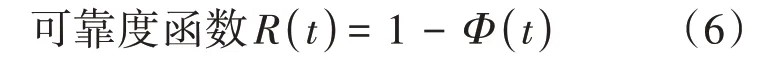
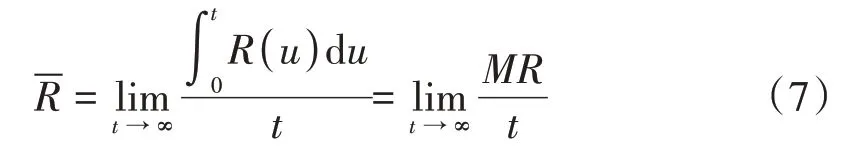
这里将可靠度看成其所在周期内的报酬,则(0,t]时间内的期望可靠度可看成(0,t]时间内的总报酬,更新极限定理见式(8)。

运用更新极限定理可得这三个指标的表达式与能够反映长期运行的系统性能,综合考虑这三个因素来确定最优预防维修周期T将更加符合实际。
2 极大模理想点法建立多目标预防维修最优化模型
将公式(4)(5)(8)按照稳态可用度极大、长期运行单位时间的期望维修费用极小和平均可靠度极大准则,建立包含三个目标和一个决策变量,即预防维修周期T的多目标最优化模型,见式(9)。
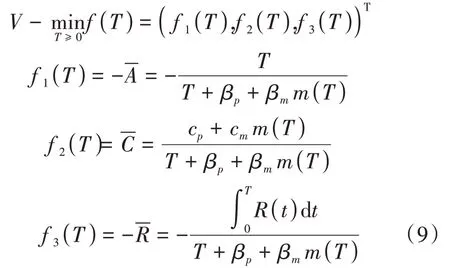
针对多目标函数问题的求解,先分别求解出每一个分目标函数的极小值,各目标函数在接近其极小值时,即取得理想点,从而获得多目标函数的解。为了体现各目标在问题中的重要程度不同,及各目标对最优预防维修周期T的影响,本研究采用理想点法中极大模理想点法[9]来求解上面多目标问题。
在进行统一量纲处理后,各分量目标函数记为F i(T),i=1,2,3,F(T)=(F1(T),F2(T),F3(T)),并求得,i=1,2,3,则F*=(F1*,F2*,F3*)为模型的理想点。
理想点法就是将目标与理想点之间的“距离”‖F(T)-F*‖作为评价函数,所以问题就转化为求解 数 值 极 小 化 问 题,其 中‖F(T)-F*‖为向量F(T)-F*的模。极大模理想点法就是采用作为评价函数求解模型。于是,将问题转化为式(10)所示的等价辅助问题。
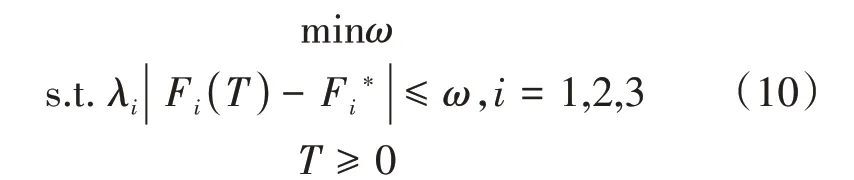
运用极大模理想点法求解模型的计算步骤如下所示。
①统一各分量目标函数的量纲。取适当的正数α分别加入各分量目标函数,得到新的各分量目标函数:f i(T)+α>0,∀T≥0,i=1,2,3;计算T≥0时各分量目标函数的极小值,以函数作为新的分量目标函数。
③检验理想点。当T*1=T*2=T*3时,绝对最优解T*=T*1,停止计算。否则转步骤④。
④给出正权数。λ1,λ2,λ3>0,且(注意要求所有λi>0)。
⑤求解辅助非线性规划问题(10),得最优解(T*,ω*),输出T*。
3 算例分析
假设某部件的寿命服从η=4×10-4(尺度参数)、β=2(形状参数)的威布尔分布。经小修后,部件恢复工作,但修复后部件的年龄不变,故障小修时间Y m的均值βm=1 h。另外,当该部件的累计工作时间达到指定年龄T时,对部件需要进行预防维修,预防维修完成后,部件恢复如新,并立即进入工作状态,预防维修时间Y p的均值βp=5 h。每次预防维修的费用c p=1 000元,每次故障小修的费用cm=100元。为使稳态可用度极大、长期运行单位时间的期望维修费用极小和平均可靠度极大,求取最优的预防维修周期T*(单位:h)。
首先,该算例中相邻两个预防维修结束时刻之间的时间构成一个更新过程。威布尔分布的寿命分布函数是所以,可靠度,故障率即部件工作时间T内发生故障的平均次数为m(T)=;平 均 周 期
根据公式(9)建立多目标最优化模型,见式(11)。
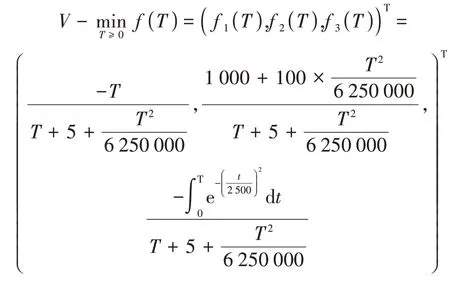
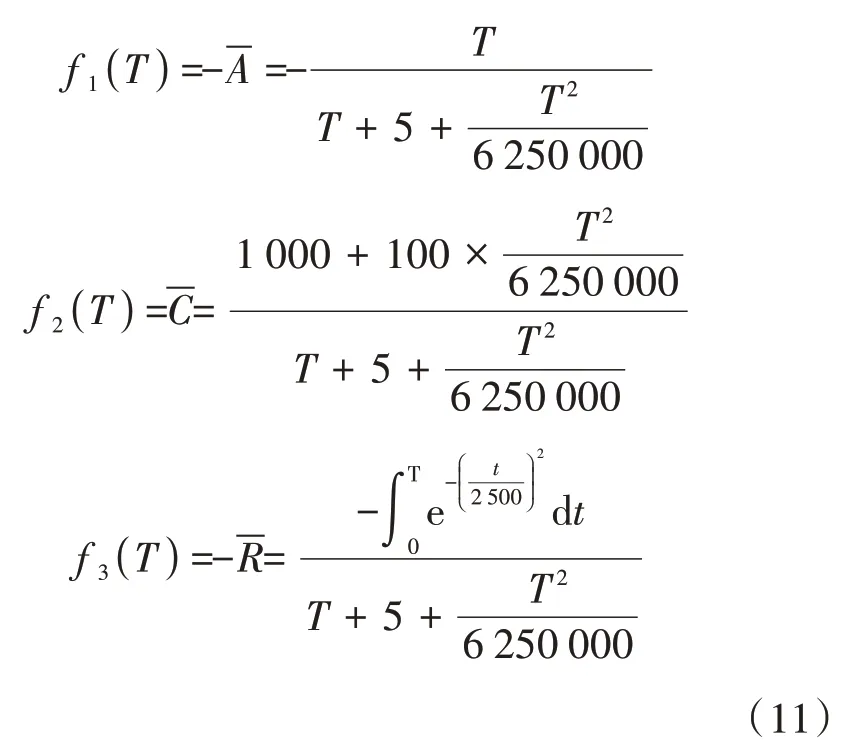
根据极大模理想点法求解公式(11),步骤如下。
①统一各分量目标函数量纲。各分量目标函数f1(T)、f2(T)、f3(T)分别加1(各分量的目标函数变为f i(T)+1>0,∀T≥0,i=1,2,3),求f i(T)+1在T≥0上的极小值(i=1,2,3):0.020 5,并由,i=1,2,3来构造新的分量目标函数,见式(12)。

③检验理想点。因为T*1≠T*2≠T*3,所以转步骤④。
④给出正权数。λ1,λ2,λ3>0,且=(1注意要求所有λi>0)。
⑤根据式(10)构造辅助非线性规划问题,由式(12)(13)可得非线性规划问题(14)。
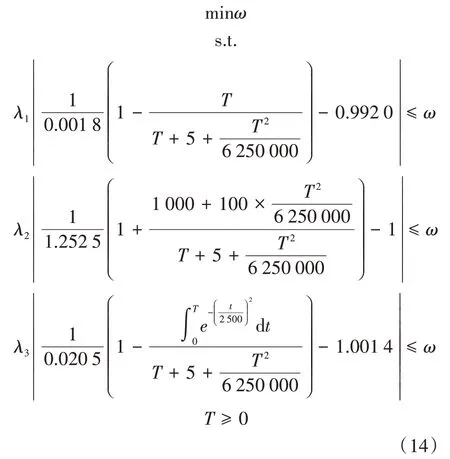
分别代入几组不同的权重来求解非线性规划问题(14),输出T*。
首先每个权重的改变对最优结果产生的影响较大,当代表稳态可用度的λ1和代表维修费用的λ2在三个权重中最大时,所得的最优预防维修周期都较大;当代表平均可靠度的λ3在三个权重中最大时,所得的最优预防维修周期都较小。这是因为部件在长期运行过程中,若考虑稳态可用度,即要保证部件处于正常状态的时间比例大,则不宜经常维修;若考虑维修费用,要让部件维修费用较小,显然也不易经常维修;若考虑平均可靠度,则要避免部件失效才能保证较高的平均可靠度,通过较频繁的预防维修可实现这一目的。所以,当三个目标同时考虑,且稳态可用度或维修费用所占权重又较大时,所得的最优预防维修周期就会较大;当三个目标同时考虑,且平均可靠度所占权重又较大时,所得的最优预防维修周期就会较小。当稳态可用度的权重相同,增大平均可靠度的权重时(因λ1+λ2+λ3=1,所以此时代表维修费用的权重λ2逐渐减小),明显可看出所得的最优预防维修周期就变小;当维修费用的权重相同,增大稳态可用度的权重时(因λ1+λ2+λ3=1,所以此时代表平均可靠度的权重λ3逐渐减小),明显可看出所得的最优预防维修周期就变大。
在系统长期运行的过程当中,需要根据不同的需求和资源限制作出不同的决策时,可以运用本研究的方法调整相关因素的权重来得到满意的结果。
