基于改进的Frantz-Nodvik方程的Yb:KGW再生放大器研究

康仁铸,吕仁冲,滕浩,朱江峰,魏志义,3,4

(1西安电子科技大学物理与光电工程学院,陕西 西安 710071;2中国科学院物理研究所,北京凝聚态物理国家研究中心,北京 100190;3中国科学院大学物理科学学院,北京 100049;4松山湖材料实验室,广东 东莞 523808)

0 引言

脉冲宽度在皮秒(10−12s)和飞秒(10−15s)量级的超短脉冲激光具有脉冲宽度窄、峰值功率高等特点,其在科学研究、生物医疗、信息通讯和材料加工等领域的需求下得到了高速发展,其中激光二极管(LD)抽运掺稀土离子镱(Yb3+)材料的全固态飞秒激光是产生高功率超短脉冲的一种有效方案。掺Yb3+激光增益介质的吸收光谱在915∼980 nm处,可使用在该波长范围内的高功率LD直接泵浦,吸收谱与发射谱波长相差较小,对应量子转换效率极高,且发射谱宽可支持百飞秒激光输出。该方案成本低且技术成熟,增益晶体加工简单,并且支持高重复频率、大能量脉冲放大。各种掺Yb3+晶体材料的出现促进了掺Yb3+飞秒激光的快速发展[1−5]。与钛宝石晶体相比较,掺Yb3+晶体的发射截面比较小,一般需要使用再生放大器作为前级放大,提升振荡器输出的功率和能量。目前基于掺Yb3+增益介质的放大器已经得到了较大程度的发展,大能量和高功率放大器的相关工作相继涌现[6−18]。2013年,Caracciolo等[7]报道了基于4 mm长Yb:CALGO晶体的再生放大器,使用116 W的泵浦获得了脉冲宽度为217 fs、平均功率为28 W、重复频率为500 kHz的激光输出结果。2016年,Andriukaitis等[8]报道了基于Yb:CaF2晶体的再生放大器,在低温条件下使用连续泵浦,在500 Hz重复频率下实现了脉冲宽度为200 fs、单脉冲能量为30 mJ的激光输出。同年,Zapata等[9]采用低温冷却的Yb:YAG晶体四通放大结构,获得了脉冲宽度为19.4 ps、单脉冲能量为2.5 mJ、重复频率为100 kHz的放大激光输出结果。2017年,Nubbemeyer等[10]基于薄片放大技术,在再生腔内使用两个薄片实现脉冲宽度为1.1 ps、重复频率为5 kHz、单脉冲能量为200 mJ的激光输出。为了抑制增益窄化并得到更窄的脉冲宽度,基于晶体不同轴向组合叠加增益光谱的双晶体放大方案和利用自相位调制展宽光谱的非线性放大方案得到了诸多发展[19−23]。再生放大器一般可以分为两个阶段:第一阶段为低Q阶段,也称为储能阶段,此阶段中晶体吸收泵浦光,积累反转粒子数;第二阶段为高Q阶段,种子激光消耗反转粒子数,获得放大。不同的再生放大器具有不同的动力学行为,决定了放大器的输出特性。一般地,人们使用速率方程来描述再生腔的动力学行为,但由于速率方程是微分方程,涉及到泵浦时间和激光在晶体中的放大行为,直接求解比较复杂。虽然Frantz-Nodvik(简称F-N)方程可以作为速率方程很好的近似,但经典的F-N方程仅适合单色放大,且假定的是没有重吸收的四能级系统,因此对动力学行为的计算显得力不从心[24]。修改后的模型虽已成功应用于基于掺Yb3+晶体再生放大器中光谱变化的模拟,但是这些模型需要密集求解和迭代计算,而再生放大中复杂的动力学过程需要大量的迭代才能达到收敛,过程比较复杂。2007年,Grishin等[25]提出了用于模拟再生放大器分叉行为的模型,该模型基于速率方程式导出简单的解析方程,但是该模型适用于单色放大且忽略了泵浦的建立过程。近年来,一种改进的F-N方程被用于描述掺钬(Ho3+)晶体放大器的行为,通过对泵浦过程和放大过程进行时间切片,得到了放大器中脉冲能量建立及光谱变化过程,其计算结果与实验结果符合得较好,并且可以用来计算放大过程中的光谱整形效应[26,27]。

本文使用改进的F-N方程对泵浦光进行了时间上的切片,并在空间上对晶体进行了切片,对掺镱钨酸钾钆(Yb:KGW)晶体再生放大器进行了仿真计算。同时自建了一套再生放大器,对其性能进行了测量,并与理论分析进行了对比研究。结果表明这种改进的F-N方程可为掺Yb3+晶体超快激光放大器的设计提供理论指导。

1 理论模拟与分析

Yb:KGW晶体可以看作准二能级结构,描述准二能级结构的速率方程为

式中:Ntot为总粒子数密度,β1、β2为各能级粒子反转分数,I为泵浦强度,Tup为上能级寿命,σabs、σem分别为吸收和发射截面,hν为光子能量。

对于准二能级固体激光放大系统,Grafenstein等[28]对经典F-N方程进行了适当的改进,使用反转分数β2来衡量增益介质中的反转粒子,但本研究中方程是对掺Ho3+晶体使用的,相比于掺Yb3+晶体,掺Ho3+晶体具有更长的上能级寿命和更小的吸收发射截面,因此,当使用同样的方法对掺Yb3+晶体的放大器进行计算时,需要进行相关的修正。此处采用的方法是在泵浦过程中对泵浦光进行切片,将泵浦光按照一定的时间长度进行M等分,将晶体沿长度进行N等分,计算每次通过晶体后的反转粒子数分布情况,切片的大小满足在每个时间-空间切片内泵浦速率相等,其原理示意图如图1所示。

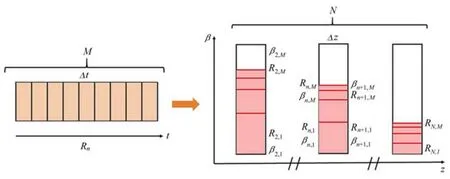
图1 泵浦过程计算示意图Fig.1 Schematic diagram of pumping processcalculation

参照Grafenstein等[28]的理论,再生放大中一个放大周期划分为泵浦过程-放大过程两个阶段。在泵浦过程中根据泵浦速率计算反转分数,饱和反转分数的表达式为

切片n与切片n+1之间的泵浦速率关系可表示为

式中:Rn是流入切片n的泵浦速率;Jsto是晶体中的储能密度;Jp,n是切片n的泵浦通量;vp是泵浦光频率;νl是信号光频率;是上能级寿命无穷大时的反转分数,可表示为

在一定泵浦速率下反转分数的变化可表示为

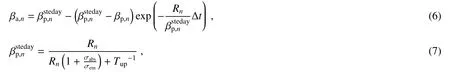
式中:βan是泵浦后切片n的反转分数,βstedayp,n是一定泵浦速率下的稳态反转分数。在放大过程中,放大器的行为主要由以下方程决定,首先根据反转分数计算波长相关增益Gn(λ,rt),即

然后,进一步计算激光通量和反转分数在放大前后的变化,分别表示为

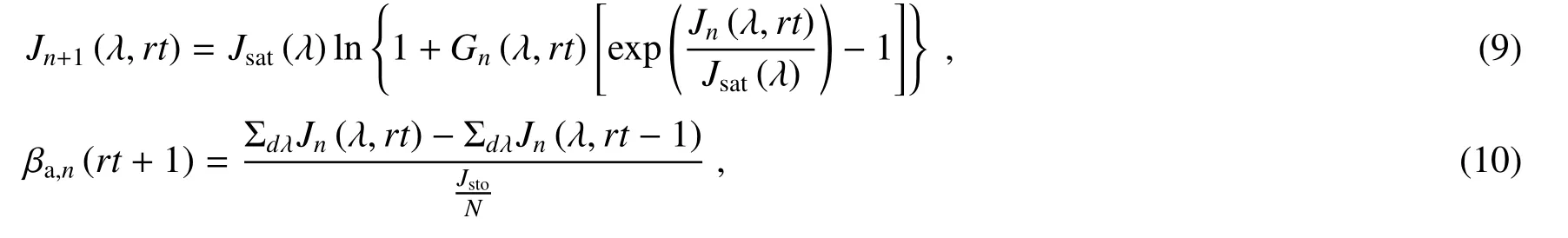
式中:Jn(λ,rt)是激光通量,Jsat(λ)是饱和通量,N是晶体在空间上分割的份数。其中饱和通量可表示为

在多色情况下,反转分数的计算需要对波长微分,独立计算各个波长下的通量变化,然后通过积分求解反转分数变化,该方法普遍适用于均匀展宽系统。在一个放大周期结束后,剩余反转分数作为下一个放大周期初始的反转分数,进而可以得到放大器的输出特性。

首先研究了晶体在稳态情况下的增益特性。在稳态条件下,即(1)式右侧为0,可以得到

进而可以计算出晶体内的泵浦分布及获得的增益,计算过程中对晶体进行切片,每个切片的厚度满足条件:泵浦光在进入切片和离开切片时,泵浦强度不发生变化。稳态条件下,泵浦在晶体内的分布可表示为

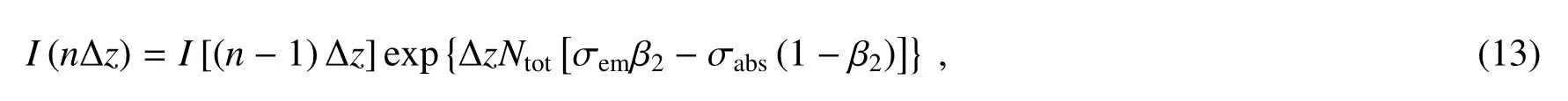
式中n为切片的序数。由(12)式计算每个切片中的粒子数分布,可以得出稳态条件下晶体的总增益为

式中σemS、σabsS分别为信号光的发射截面、吸收截面。晶体长度和泵浦强度共同决定了稳态下增益的大小,为了优化设计,计算了增益与泵浦强度和晶体长度的关系,分别如图2、3所示,模拟中所用到的计算参数如表1所示。

表1 模拟计算中所用Yb：KGW晶体的参数Table 1 Parameters of Yb:KGW crystal used in the simulation

图2为晶体增益与泵浦强度的关系,其中设定晶体长度为5 mm,当泵浦强度高于晶体饱和功率密度时增益开始饱和,最佳泵浦强度为40 kW/cm2。在此功率密度下,图3给出了晶体增益与晶体长度的关系,由图可见最佳的晶体长度为5.45 mm,与设定相差较小。

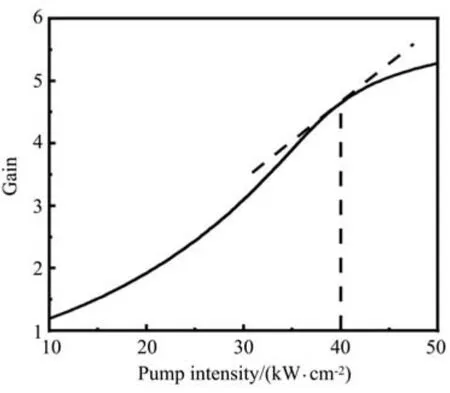
图2 晶体增益与泵浦强度的关系Fig.2 Gain of crystal as a function of pump intensity

图3 晶体增益与晶体长度的关系Fig.3 Gain of crystal as a function of crystal length

稳态情况给出了在一定泵浦强度下晶体的最大增益,同样地,泵浦时间也是非常重要的参量。通常,在kHz及以下重复频率时,Yb:KGW常采用准连续泵浦,泵浦时间一般为ms量级。根据上文所述模型,计算了不同泵浦强度和泵浦时间下晶体增益的变化,如图4所示。泵浦强度越高,达到增益饱和所需的泵浦时间越短,在40 kW/cm2的泵浦强度下,晶体增益达到饱和所需时间为420µs。这也意味着,如果在1 kHz重复频率下使用准连续泵浦,泵浦时间大于420µs即可。使用准连续泵浦可以减小泵浦光在晶体上的作用时间,进而降低晶体的热效应,得到更好的热管理效果。

图4 不同泵浦强度下晶体增益与泵浦时间的关系Fig.4 Gain of crystal as a function of pump time at different pump intensity

同样地,激光放大的重复频率限制了泵浦时间,进而影响了输出性能。基于所用模型计算了1、2、5、10 kHz下的输出能量,如图5所示。为计算方便,这里使用了单色近似,即认为放大光只具有单一波长。在1 kHz重复频率下,计算得到最大输出能量为1.3 mJ。由计算可知,泵浦时间大于420µs时,晶体的增益已经饱和,因此,在2 kHz重复频率下输出脉冲能量基本不变。Yb:KGW晶体的荧光寿命为330µs,在重复频率大于3 kHz时,可以认为再生放大器工作在高重频状态,需要使用连续泵浦。随着放大器重复频率的提高,晶体获得的增益变小,所需放大程数(种子光在再生腔内往返振荡放大的次数)相应增加,所能得到的最大输出能量也相应下降。

图5 不同重复频率下再生放大器输出特性Fig.5 Output characteristics of regenerative amplifier at different repetition rates

2 实验设计与讨论

根据所计算的模型结果,自建了一个再生放大器进行实验,其光路如图6所示。种子光为光纤种子光源,中心波长在1030 nm,注入再生腔的单脉冲能量为1 nJ。再生腔的泵浦光为光纤耦合输出的半导体二极管(LD),其输出波长为979 nm,最大输出功率为50 W。输出光纤芯径为105µm,经过1:3的透镜成像在晶体上,其焦点在距晶体表面1/3长度的位置。所用晶体为3 at%掺杂、3 mm×3 mm×5 mm的Yb:KGW,晶体沿Ng轴切割。为了得到更有效的散热效果,晶体表面用铟箔包裹并在加热炉中加热,使晶体焊接在水冷热沉上。

图6 Yb:KGW再生放大器示意图Fig.6 Schematic diagram of Yb:KGWregenerative amplifier

实验测量了晶体在1 kHz重复频率下的输出性能,在40 W泵浦的情况下,种子光在再生腔内往返51次时得到了最大1 mJ的放大输出。相比于仿真计算得到的结果,输出能量明显较小。这种差异来源于几个方面:首先,计算时认为激光在晶体内是均匀分布的,且光斑大小与泵浦光光斑大小一致并完全重合,实际上激光在晶体内为高斯分布,并且与泵浦光的重合度不为1;其次,在仿真计算过程中给出的腔内损耗为10%,实际搭建过程中,可能因为腔内元件质量以及热效应的影响引入了更多的损耗。同样地,在使用准连续泵浦条件下,泵浦时间设置为450µs,得到的输出结果与连续泵浦情况下相同,这也验证了计算的合理性。

进一步测量了放大器在不同重复频率下的输出性能,如图7所示。随着重复频率的增加,在1∼5 kHz时,激光放大后的平均功率呈线性增加;在6∼10 kHz时,激光放大后的平均功率近乎不变。整个过程中单脉冲能量呈线性降低。以上基本变化趋势与计算结果相符,但由于实验中的损耗等因素造成整体输出能量有所下降。其中放大器重复频率在6 kHz时出现拐点,输出能量和对应的平均功率均有所下降,这是由于在实验中发现当放大器工作在此重复频率时出现了倍周期分叉现象,为了得到稳定的激光放大输出,减少了再生腔内的放大程数,因此在此处放大器输出功率降低。

图7 不同重复频率下再生放大器的输出能量与平均功率Fig.7 Average output power and pulse energy of regenative amplifier versus different repetition rates

该模型可以预测激光的脉冲分叉行为,这在高重复频率放大中是影响放大器性能的重要因素。根据不同的泵浦时间和放大程数,可以计算晶体在不同重复频率放大时的动力学行为。如图8所示,模拟了在50 kHz重复频率下,随着放大程数的增加,放大器出现倍周期分叉,进而表现出混沌现象的过程,后续可以结合理论分析对高重复频率放大器的行为开展进一步研究。

图8 倍周期分叉计算:再生放大器输出能量随放大程数的变化Fig.8 Calculated bifurcation diagram:Output energy of regenerative amplifier versus the round trip

3 结论

基于改进的F-N方程,对掺Yb3+晶体再生放大器的动力学行为进行了研究,并结合实验结果证明了理论分析的合理性。此模型可以进一步指导和优化掺镱晶体再生放大器的设计。该模型同样可以用于CPA系统的优化设计,通过计算不同波长的增益并设计不同的滤波器参数,可以有效抑制再生放大过程中的增益窄化,有望实现高功率、大能量、窄脉宽的激光输出。