单层原子的厚度对等离激元色散关系的修正

吴仍来,余亚斌,肖世发,全军

(1惠州学院电子信息与电气工程学院,广东 惠州 516007;2湖南大学物理与微电子科学学院,湖南 长沙 410082;3岭南师范学院物理科学与技术学院,广东 湛江 524048)

0 引言

等离激元因其独特的场增强和突破衍射极限的特性在光信息传输和采集、纳米电路构造和设计、单分子信号检测和光谱学、量子通信和计算等领域具有重要的应用价值[1−5]。目前,低维纳米光电器件中的等离激元引起了较多关注,其能充分利用低维材料比表面积大、光吸收充分、能耗低等优良特性,能支持更长距离的等离激元光波导,并获得更低辐射损耗、更长寿命的等离激元[2,6,7]。

在低维体系中,二维模式的等离激元因其无能隙、易激发的特性,会影响到准二维结构的电导、热导以及光吸收等特性[8−16]。早期文献和固体理论书籍中较多地给出了准二维体系中纯二维等离激元色散关系的解析解[7−12],但这些研究中大部分采用了严格的约束条件:电子的运动被严格限制在平面层方向,在垂直平面方向上几乎没有运动。因此这类研究不能有效反应原子层的厚度对等离激元的影响。为了探讨准二维体系的厚度对等离激元的影响,文献[16]测量了极低密度下33 nm厚的准二维GaAs体系等离激元的色散关系,文献[17-19]通过理论计算解释了文献[16]的实验结果,考虑了厚度对等离激元的影响。但这些求解过程采用了低密度条件,对电子密度比较大的体系是否适用尚未可知,同时文中没有给出波矢比较大时的结果,也没有给出非近似下的精确结果。为了进一步加强对该问题的理解,本文利用自由电子气体模型求解了单层原子体系等离激元色散关系的解析解,分析了单层原子体系的厚度对等离激元色散关系的影响,并给出原子层厚度对等离激元频率的一阶修正。本文结果对电子数密度比较大的情形同样适用,可作为文献[17-19]结果的一种补充。

1 模型及方法

图1给出单层原子体系的模型图,该体系在x-y平面上的面积为S,原子层的厚度为d。令a=d/2,a表示竖直方向上电子被束缚在离原子距离为a的边界范围内。

图1 单层原子体系的模型图Fig.1 Model of monolayer-atom system

设r和k分别为电子在x-y平面上的位置矢量和波矢,z和kz分别为电子在竖直方向上的坐标和波矢。考虑表面积S足够大,在水平方向上电子的波函数为平面波,而竖直方向上电子处在无限深势阱中,则本征波函数可写为

式中

式中:kz=nπ/(2a),n为量子数。

根据准二维体系满足的线性响应理论,在外部电势Vex(z,q,ω)的作用下,原子层内部的电荷密度响应为[19,20]

式中:q为波矢,外部电势使电子的波矢从k变到k+q,q代表外部电势给电子带来的动量增量;ω代表电势的驱动频率;V(z′,q,ω)=Vex(z′,q,ω)+Vin(z′,q,ω),含外加电势和内部诱导电势两部分,其中Vin(z′,q,ω)是内部电荷的库仑作用导致的内部电势;Π(z,z′,q,ω)为林哈德函数,可表示为

式中前面的因子2表示忽略电子自旋的影响,同一个量子态容纳两个电子;Ek是电子在x-y平面上的本征能量;Ekz是电子在z方向的本征能量;f(Ek+Ekz)为费米函数;由于电子只处在第一布里渊区,kz==π/(2a);对于自由电子气体,根据本征能量和波矢的关系有Ek=ħ2k2/(2me),Ek′z=Ekz=ħ2kz2/(2me),me为电子质量,则

进一步,根据电磁学理论中的高斯定理,体系内部诱导电势满足泊松方程

式中ε0是真空中的电介质常数,∇2r为水平面方向上的拉普拉斯算符。根据内部电势和电荷的傅里叶变换有

将(7)、(8)式代入(6)式,可得

将(5)式代入(10)式可得非齐次方程

式中左边括号部分为一维拉普拉斯算符,对应的格林函数为[21]

将格林函数代入(11)式可得

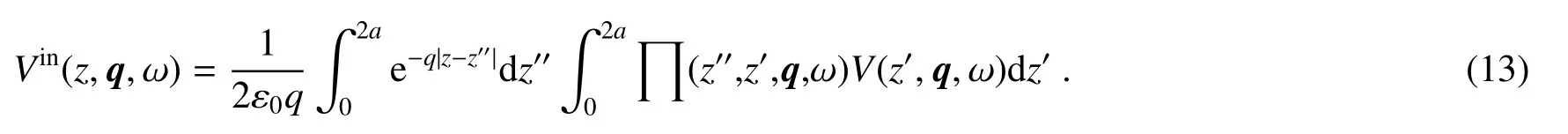
将(5)式代入(13)式,可得

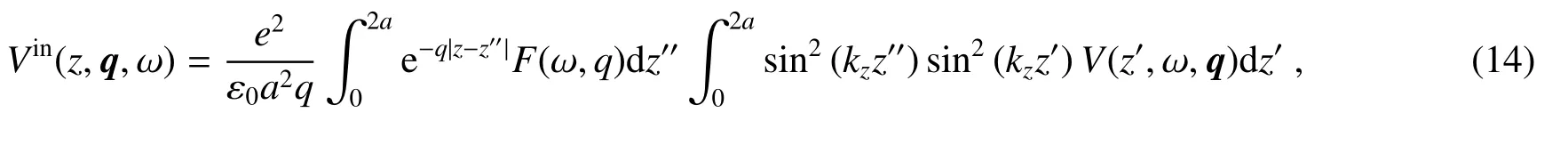
式中

令

在方程(14)的左右两边同时乘以sin2(kzz)再对z积分,可得其等价方程

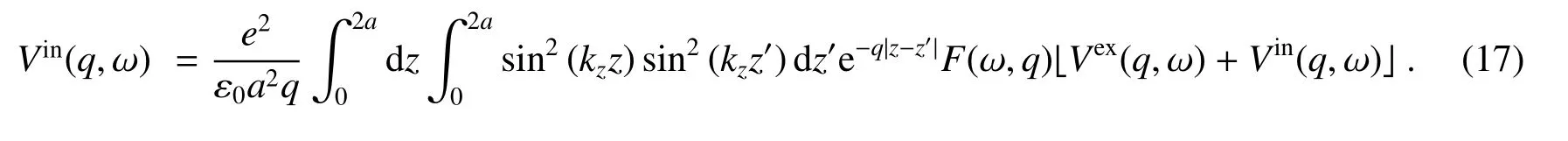
令

则(17)式可简化为

由于等离激元是体系的固有性质,与外加电场无关,可令Vex(q,ω)=0,则(19)式简化为

此式即为电势在波矢空间的集体振荡的本征方程。方程(20)中Vin(q,ω)的系数为复数,当

时,Vin(q,ω)有极大值,此时电荷发生集体振荡,由(21)式解出来的集体振动频率即为等离激元频率。

2 等离激元的色散关系求解与讨论

利用(21)式,只要求得ν(q)和F(ω,q)即能得出等离激元的色散关系。(15)式中F(ω,q)经积分运算可得

式中:kF为费米波矢,其与总电子数Ne的关系为

对(23)式积分,可得

整理后可得

式中nS为电子数面密度,与总电子数的关系满足Ne=nSS。(25)式代入(22)式得

(18)式中的ν(q)经积分后可得

考虑无阻尼情况η=0,将(26)、(27)式代入(21)式,可得单层原子体系等离激元色散关系的精确解

由于求解过程没有进行任何的低密度近似和长波近似,(28)式的结果适用于高电子密度下的短波情形。

基于(28)式开根号算出的结果,图2给出不同厚度单层原子体系等离激元的色散曲线,并与纯二维体系等离激元的色散曲线进行比较,其中最上面那条曲线对应纯二维体系,其他曲线由上往下依次对应a=0.05,0.15,0.25,0.35,0.45,0.55 nm的单层原子体系。纯二维体系的等离激元能量由文献[8,12]中高斯制下的表达式给出,变换到国际标准单位则为,其中ω0表示纯二维等离激元频率。计算中取nS=1.63×1019/m2,该电子密度是文献[16-19]中电子密度的105倍以上,属于高密度情形,同时波矢取值包括了长波和短波范围。

图2 单层原子和纯二维体系等离激元的色散关系Fig.2 Plasmon dispersion of monolayer-atom system and pure 2D system

由图2可知,单层原子体系的等离激元色散曲线相比纯二维的更低,原子层厚度对等离激元的能量会产生负的修正。原子层越薄,等离激元的能量越趋近纯二维等离激元能量;原子层越厚,等离激元的能量越小,越偏离纯二维等离激元的能量。产生该结果的原因如下:面电子数密度不变的情况下,由(25)式可知费米波矢和费米能级会随着原子层变厚而减小,电子在费米能级附近集体激发所需要的能量变低,等离激元的能量会减小。上述结果与文献[16∼19]中准二维GaAs量子阱的实验和理论结果类似,说明本研究得出的结果在低密度情况下同样适用。同时图2将短波情形也考虑进去,可看出随q增大,等离激元能量随原子层的变厚下降得更明显,长波下q很小时,原子层的厚度对等离激元能量的影响很小。

进一步给出长波近似下,qa≪1时等离激元色散关系的近似解。(27)式中ν(q)作近似≈1−2qa+2q2a2,π2/a2+q2≈π2/a2,可得

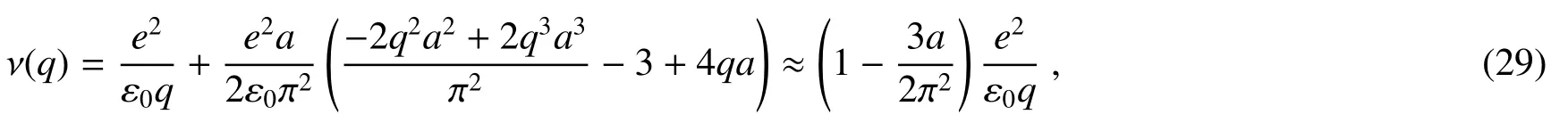
(29)式代入(28)式,等离激元的能量忽略比q更高次幂的项,可得色散关系的近似表达式

3 结论

研究了单层原子体系中等离激元的色散关系,得出单层原子体系的等离激元色散曲线相比纯二维的更低,且随原子层变厚,费米能级变低,导致等离激元能量减小;同时,随波矢增大,原子层的厚度对等离激元频率的相对修正也增大。在长波近似下,还给出了单层原子体系等离激元色散关系的一阶近似,可清晰表明等离激元频率随原子层的厚度和波矢的变化关系。本研究中等离激元的色散关系可用于解释单层准二维电子系统(如GaAs、单层金属原子体系)中,原子层的厚度对等离激元的影响,对单层石墨烯、硅烯的等离激元也具有定性的指导意义。