化归思想在初中数学解题中的运用
2022-08-22江苏省无锡市凤翔实验学校
⦿江苏省无锡市凤翔实验学校 马 琦
1 引言
当前初中生在数学学习过程中存在着这样的现象:他们关注更多的是这道题做对了没有;如果错了,是在哪一步出错.他们没有在宏观上去关注这道题,即这道题体现的数学思想是什么,用这样的思想还能解答哪些类似的题目.其实当学生从数学思想的角度去探究问题时,会在“山重水复”中窥见“柳暗花明”.因此,在教学中教师要培养学生关注数学思想的意识,比如培养学生化归思想,以提升他们的学习能力.运用化归思想解决数学问题,就是在研究和解决有关数学问题时,教师要指导学生先思考采用什么样的手段将问题进行转化,而不是具体的解题步骤.
2 由陌生引向熟悉,体会化归思想
教师要培养学生的读题能力,即学生解题时,先要让他们以自己的方式解读这道题.学生在读题的时候,要能读出这道题中有哪些是熟悉的,有哪些是不熟悉的认知、问题.当学生大致认清题目的面目之后,教师就可以引导他们将陌生的问题转化为熟悉的问题,在运用中体现化归思想.
以苏科版九年级上册“直线与圆的位置关系”这一章节为例,教师设置这样的题目:如图1所示,AB是⊙O的弦,点C在过点B的切线上,OC⊥OA,OC交AB于点P.若∠BPC=70°,则∠ABC的度数等于多少?

图1
学生发现题目中的条件都是一些常见的条件,无非就是某条直线与某个线段垂直,某个角等于多少度,但是发现要求的这个角度是陌生的,这个陌生体现在它几乎与题面上任何角都没有关系.教师要指导学生进行角度之间的转化,让化归思想体现出来.学生先是从∠ABC这个陌生的角入手,将其转化为“∠OBC-∠OBA”.这其中∠OBC的度数可以从“点C在过点B的切线上”这一条件获得,即∠OBC为90°;也就是说,学生将完全陌生的角转为一个熟悉的角与另一个陌生的角的差,接着继续将∠OBA进行转化.根据题目图形,学生不难得出“∠OBA=∠A”这一结论,但∠A也是一个陌生的角.再次转化,发现在∠A所在的三角形中,因为OC⊥OA,所以∠AOC=90°,所以可将∠A转化为“90°-∠APO”.而∠APO也是一个陌生的角,题目中没有提及,但是题目中提到的是它的对顶角∠BPC等于70°,进而学生再次转化,得出∠APO等于70°.很显然,在这个题目中学生秉持的理念就是要将不熟悉的角度进行转化,只是这个转化不是一步到位,需要经过多次转化,最后变成学生熟悉的问题情境.因此,在教学中,教师可指导学生将问题分为熟悉的与不熟悉的两大类,再在中间不断地转化,进而达到化解问题的目的.
3 由特殊引向一般,了解化归思想
学生解题时会遇到具体的问题情境,即要求学生运用所学的知识解决实际生活中的问题.对于这样的题目学生可以运用化归思想进行层层转化,将特殊的问题转化为一般性的问题,进而为问题的解决提供便利[1].
以苏科版数学八年级上册“勾股定理”为例,教师将这样一道题展示给学生:今有竹高一丈,末折抵地,去本三尺,问折者高几何?这是《九章算术》里的一道题,教师想让学生在运用化归思想的同时,感知中国古人的智慧.学生将这段文言文转化为白话文:一根竹子原高1丈,中部有一处折断,竹梢触地面处离竹根3尺,试问折断处离地面多高?教师首先要求学生将题目的文字内容转化为图形,并按照题目的要求将相关的数据标出来,然后引导学生将题目中“竹子”这一特殊的情境换掉,变成一个一般性的图形.换言之,教师指导学生进行特殊性到一般性的转化.
学生将原题中的已知条件转化成图2,对照这个图形,首先假设A,B之间的距离为x尺,依据题意可知A,C之间的距离就为(10-x)尺,因为题目中BC的距离是3尺,依据勾股定理,列出x2+32=(10-x)2.从整个过程来看,教师主要指导学生从特殊的情境中看到一般性的问题.学生要能将原题目的一些特殊性的表述转为一般的数学化的叙述,进而促成问题的解决.教师指导学生由特殊性到一般性转化的过程就是展示化归思想的过程.

图2
4 由复杂引向简单,应用化归思想
学生在学习数学的过程中遇到的常见的困难就是不会将复杂的问题转化为简单的问题.化归是重要的数学思想,最主要的就是在不停的转化中将问题解决.将复杂转为简单就是化归思想的主要展现形式.由复杂往简单转化,主要是将复杂的问题简化,当然也包括将复杂的表述简化.
以苏科版数学七年级上册“一元一次方程的应用”为例,教师设置这样的题目:某公司会计欲查询乙商品的进价,发现进货单已被墨水污染,如表1.
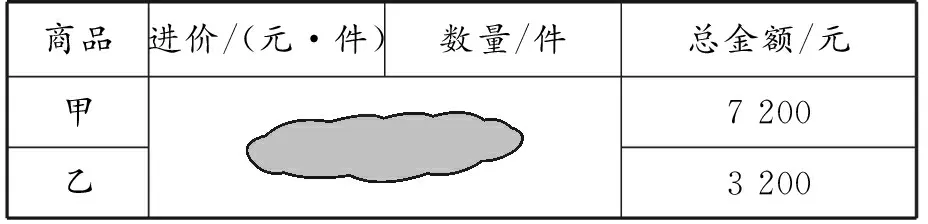
表1 进货单
商品采购员A和仓库保管员B对采购情况回忆如下:
A:甲商品进价比乙商品进价每件高50%.
B:甲商品比乙商品的数量多40件.
请你求出乙商品的进价,并帮助他们补全进货单.

5 结束语
化归不仅是一种重要的解题思想,也是学生在学习数学的过程中应具有的最基本的思维策略,当然也是一种有效的数学思维方式.学生学习数学的过程就是不断改变思维策略、提升思维品质的过程.换言之,在教学过程中,教师要关注学生的思维发展,进而促进他们素养的生成.教师重视化归思想在解题中的运用,其实也就是重视学生思维能力的培养,只是将思维的培养进一步上升到宏观的高度,居高处临下,于高屋处建瓴[2].
