线段之妙 彰显数学之美

⦿湖北省利川市教学研究和教师培训中心 罗仁义⦿湖北省利川市建南镇民族初级中学 李小勇

1 原题呈现

图1

(2019年恩施州中考第23题)如图1，在⊙O中，AB是直径，BC是弦，BC=BD，连接CD交⊙O于点E，∠BCD=∠DBE.

(1)求证：BD是⊙O的切线；

2 试题感悟

题目中由条件“过点E作EF⊥AB于点F，交BC于点G”给出的线段EF，在解题时的作用妙不可言，彰显了数学之美，是本题的“点睛之笔”.其原因有三：其一，这条线段EF虽然在第(2)问中才出现，但它可以作为第(1)问中的辅助线，为第(1)问的证明拓展了思路，学生可以选用“垂径定理”“圆周角定理”“圆弧、圆周角、圆心角之间的等对等关系”等圆的基本性质来完成.其二，由于线段EF与BC相交于点G，第(2)问中要求的线段BG就是△BEG或者△BGF的边，如果选择用△BEG来求线段BG的长，就用“相似三角形”的知识来解决问题；如果选择用△BGF来求线段的长，就用“勾股定理”的知识来解决问题.其三，由于线段EF的出现，图形中又出现了一个等腰三角形CEG和几组相似三角形(如:△BGE∽△BEC，△CGE∽△CBD，△GEC∽△EDB，△DEB∽△DBC)和一组直角三角形(Rt△BEF与Rt△BGF).

在考试过程中，考生充分展示了他们的数学素养：考生用他们熟悉的“圆的基本性质”来找角的关系，用等角对等边来确定线段的长度，用相似三角形找比例关系，用勾股定理列方程，熟练地进行计算，准确地解方程，规范地书写答题过程.此题在实现考查和选拔功能的同时，也为考生提供了广阔的思维空间；在考查学生数学知识的整合能力、探索解题过程的思维品质的同时，也为初中数学教学起到了很好的导向作用.此题根植于教材，又高于教材，是一道好题.

3 考生的解题赏析

3.1 第(1)问的解法赏析

思路一：利用直径构建直角.

图2

解法1：如图2所示，连接AE.

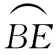
∴∠A=∠C.

∵∠BCD=∠DBE，

∴∠A=∠DBE.

∵AB是⊙O的直径，

∴∠AEB=90°.

∴在△ABE中，

∠EAB+∠EBA=90°.

∴∠DBE+∠EBA=90°，即∠DBA=90°.

∴AB⊥BD.

又∵AB是⊙O的直径，

∴BD是⊙O的切线.

(说明：这是命题组给出的参考答案，思路直接，过程简洁.)

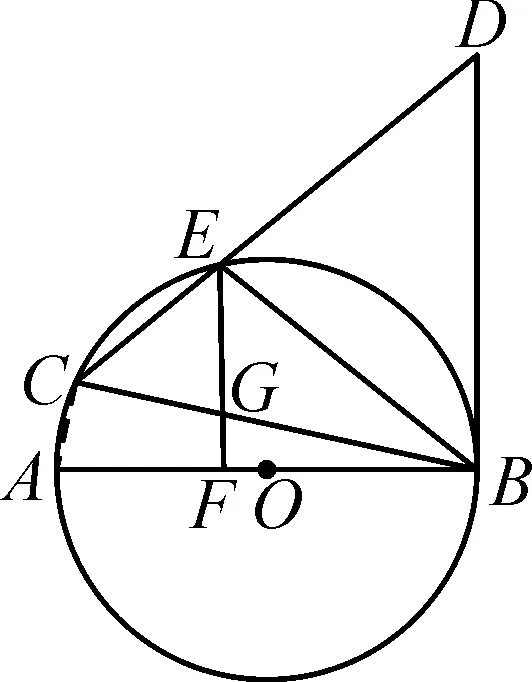
图3

解法2：连接AC，如图3所示.

在△DBE与△DCB中，有

∴△DBE∽△DCB.

∴∠DEB=∠DBC.

又∵四边形ABEC是⊙O的内接四边形，

∴∠DEB=∠A，

∴∠DBC=∠A.

∵AB是⊙O的直径，

∴∠ACB=90°.

∴在△ABC中，∠A+∠CBA=90°，

∴∠DBC+∠CBA=90°，即∠DBA=90°.

∴AB⊥BD.

又∵AB是⊙O的直径，

∴BD是⊙O的切线.

(说明：这里用到了圆内接四边形的性质，反映出教师在教学过程中对这个基本性质进行了拓展.)

图4

解法3：如图4所示，连接EO并延长，交⊙O于点M，再连接BM，则EM是⊙O的直径，

∴∠EBM=90°.

∴在△EBM中，

∠M+∠BEM=90°.

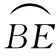
∴∠M=∠C.

又∵∠C=∠DBE，

∴∠M=∠DBE.

∵BO=EO，

∴∠OEB=∠OBE.

∴∠DBE+∠OBE=∠BEM+∠M=90°，

即∠DBA=90°.

∴AB⊥BD.

又∵AB是⊙O的直径，

∴BD是⊙O的切线.

(说明：这种解法就是解法1的“翻版”，略显复杂.考生在答题时能够想到这种方法，但为什么没想到连接AE呢？反映了考生的紧张心态.事实上，在解法2的基础上，也可以进行类似的翻版，只不过更复杂，因此不可取.)

思路二：利用第(2)问“过点E作EF⊥AB于点F”的提示来解答.

图5

解法4：延长EF交⊙O于点H，如图5所示.

∵在⊙O中，AB⊥EH，

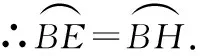
∴∠BCE=∠BEH.

又∵∠BCD=∠DBE，

∴∠BEH=∠DBE.

∴EF∥BD.

∵EF⊥AB于点F，

∴BD⊥AB于点B.

又∵AB是⊙O的直径，

∴BD是⊙O的切线.

(说明：这种解法把第(2)问中的“过点E作EF⊥AB于点F”作为第(1)问解答的辅助线，这也是此题的巧妙之处，给考生提供了更多的解题思路.有的考生利用这个提示，进行了较为复杂的角的转换，虽然可以达到解题的目的，但不可取.)

思路三：利用圆弧的度数来解答.

解法5：如图1,

∵AB是⊙O的直径，

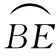
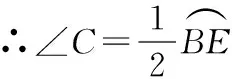
∵∠BCD=∠DBE，

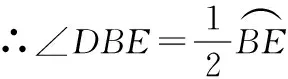
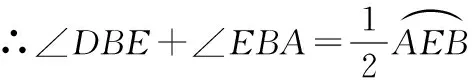
∴AB⊥BD.

又∵AB是⊙O的直径，

∴BD是⊙O的切线.

(说明：考生的这种解法反映出教师在教学过程中补充了圆弧的知识，拓展了学生的解题思路.)

图6

解法6：连接EO，如图6所示.

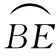
∵∠BCD=∠DBE，

∵BO=EO，

∴∠OEB=∠OBE.

在△BOE中，∠BOE+∠BEO+∠EBO=180°，

∴∠DBE+∠EBO=90°，即∠DBA=90°.

∴AB⊥BD.

又∵AB是⊙O的直径，

∴BD是⊙O的切线.

解法7：连接EO，如图6所示.

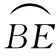
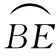
∵∠BCD=∠DBE，

∴AB⊥BD.

又∵AB是⊙O的直径，

∴BD是⊙O的切线.

(说明：这两种解法与参考答案，即与解法一有异曲同工之妙，也有考生在此基础上过点O作BE的垂线，同样可以解决问题，只是略显复杂.)

3.2 第(2)问的解法赏析

思路一：利用三角形相似求解.

解法1：如图1所示，

∵在△BCD中，BC=BD，

∴∠C=∠D.

∵∠BCD=∠DBE，

∴∠D=∠DBE.

∵EF⊥AB于F，

∴∠EFA=90°.

∵∠DBA=90°，

∴EF∥BD.

∴∠CEG=∠C,∠DBE=∠BEG.

∴CG=EG=3.

又∵∠BCD=∠DBE，

∴∠BEG=∠C.

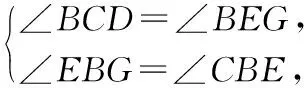
∴△BEG∽△BCE.

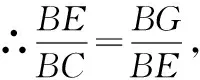
解方程，得BG=5或-8(舍去).

因此，BG的长为5.

(说明：这是命题组给出的参考答案，过程简洁，但考生的思维还是不容易达到这个高度.)

解法2：如图1所示,

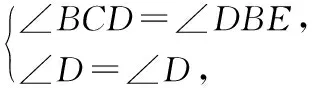
∴△DBE∽△DCB.

即BD2=DE·DC

∵EF⊥AB于点F，

∴∠EFA=90°.

∵∠DBA=90°，

∴EF∥BD.

∴∠CEG=∠D.

又∵BC=BD，

∴∠C=∠D.

∴∠C=∠CEG.

∴CG=EG=3.

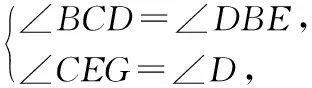
∴△GEC∽△EDB.

∴BD2=40+3BD.

解这个方程，得BD=8或-5(舍去).

因此BG=BC-CG=8-3=5.

所以，BG的长为5.

思路二：利用勾股定理求解.

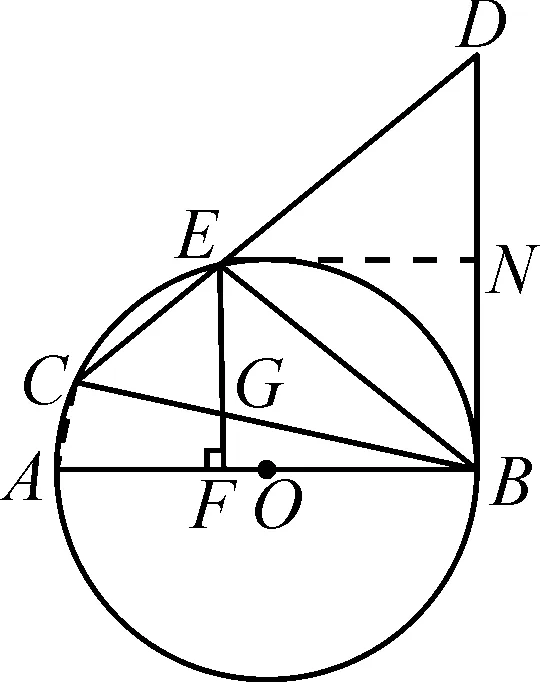
图7

解法3：如图7所示,过点E作EN⊥BD于点N.

由BC=BD，得∠C=∠D.

∵∠BCD=∠DBE，

∴∠D=∠DBE.

∵EF⊥AB于点F，

∴∠EFA=90°.

∵∠DBA=90°，

∴EF∥BD，

∴∠CEG=∠D.

∴∠C=∠CEG.

∴CG=EG=3.

∴BD=BC=BG+3.

在△BED中，BE=ED，EN⊥BD

在Rt△BEF中，有

在Rt△BGF中，有

整理，得BG2+3BG-40=0.

解这个方程，得BG=5或-8(舍去).

因此，BG的长为5.

解法4：延长EF交⊙O于点H，连接BH，如图8所示.

图9

∵在△BCD中，BC=BD，

∴∠C=∠D.

∵∠BCD=∠DBE，

∴∠D=∠DBE.

∵EF⊥AB于点F，

∴∠EFA=90°.

∵∠DBA=90°，

∴EF∥BD.

∴∠CEG=∠C.

又∵∠C=∠H，∠CEG=∠GBH，

∴∠H=∠GBH.

∴GB=GH.

∵在⊙O中，AB⊥EH，

∴EF=HF.

∴BG=HG=HF+GF=EF+GF=3+2GF.

在Rt△BEF中，有

在Rt△BGF中，有

BF2=BG2-GF2=(2GF+3)2-GF2.

整理，得2GF2+9GF-11=0.

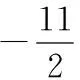
∴BG=3+2GF=3+2=5.

因此，BG的长为5.

(说明：题目给考生提供了广阔的思维空间，考生给出了多种不同的解答方法.线段EF，妙！)

4 教学启示

首先，教学必须立足课本.用教材进行教学的关键是把知识的脉络理清楚.针对课本中的基本概念、性质、定理、基本图形，学生不仅要知其然，还要知其所以然；不仅要“会用”，还要弄清楚知识的来龙去脉，深刻理解知识的本质.认真研究和挖掘课本中习题的深层次价值，挖掘概念的内涵和外延，归纳总结重要图形和方法，并尝试做一些拓展，发挥出课本的最大价值.几何综合题的教学要狠抓基础(基本图形、基本知识、基本方法等)，积极渗透数学思想方法，培养学生分析问题、解决问题的能力.同时，还要培养学生的独立思考能力：怎么去思考问题，怎么去找突破口，为什么这样，为什么不这样，还有更好的方法吗……

其次，注重发展学生的推理能力.《义务教育数学课程标准》中明确指出：“要培养学生的运算能力、发展逻辑思维能力.”因此，培养学生的能力，特别是逻辑推理能力是初中数学教学的核心，也是推进素质教育的一个重要手段.我们要加强对数学教学现状的反思和对“新课标”的学习，在课堂教学中落实合情推理与演绎推理并重的教学思路，力求让学生在知识获得的过程中有所悟，从而了解知识的来龙去脉和内在联系，形成对数学的真正理解，为学生的继续学习提供条件.

最后，欣赏完考生们的各种解题方案，感觉真是八仙过海，各显神通，美不胜收啊！我们为师者，不能局限于传道、授业、解惑，而是要善于利用数学之美，激励和唤醒学生，鼓励他们做学习的主人.