思路有序变化 变式自然生成

⦿湖北省武汉市吴家山第三中学 万建光

1 引言

抛物线中的定值问题是中考的热点，这类试题注重初高中知识的衔接,考查学生解题的综合能力，备受命题者的青睐.如何根据此类问题编制变式题组？变式又是怎样产生的？还能编出哪些定值问题？这些都是数学教师和学生一直思考的问题.本文以2020年武汉市中考数学第24题第(3)小题为例，运用多种策略和方法对题目进行变式研究，并探究同一背景下的其他定值问题，以期和大家共研变式教学之道.

2 试题呈现

题目将抛物线C：y=(x-2)2向下平移6个单位长度得到抛物线C1，再将抛物线C1向左平移2个单位长度得到抛物线C2.

(1)略；(2)略；

图1

3 变式研究

第(3)问的问题是自然的，对学生的智力有适度的挑战性，题意明确、不纠缠于细枝末节，表述形式简洁、流畅、好懂[1].多维度、多层面对这个“好题”进行变式研究，有利于夯实学生的基础知识和基本技能，有利于扩大学生的认知广度和深度.原题的核心条件有：(1)两条直线EF，GH相交于点O；(2)点M，N分别是线段EF，GH的中点；(3)两条直线的斜率之积为-4.保持原题抛物线的解析式及部分核心条件不变，编制母题，在母题的基础上进行变式研究.

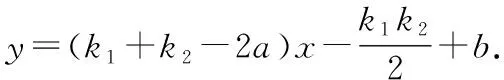
3.1 交点变化，定点依然

思路1：原题中两条弦的交点在坐标原点，可以改变核心条件中两弦交点的位置来探究直线是否过定点.

图2

变式1如图2，直线y=k1x+b1和直线y=k2x+b2交于点P(1，3)，直线y=k1x+b1与抛物线y=x2-6交于点E，F，直线y=k2x+b2与此抛物线交于点G，H, 且M，N分别为线段EF，GH的中点，若k1k2=-4，求证：直线MN经过一个定点.(参考答案：定点为(0，5).)

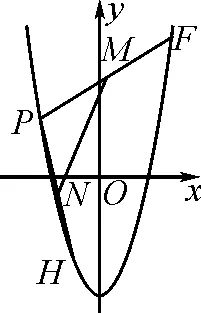
图3

变式2如图3，点P(-3，3)在抛物线y=x2-6上，直线PF:y=k1x+b1与此抛物线交于另一点F，直线PH:y=k2x+b2与此抛物线交于另一点H，且M，N分别为线段PF，PH的中点，若k1k2=-4，求证：直线MN经过一个定点.(参考答案：定点为(0，5).)

图4

变式3如图4，直线y=k1x+b1和直线y=k2x+b2交于点P(-4，3)，直线y=k1x+b1与抛物线y=x2-6交于点E，F，直线y=k2x+b2与抛物线交于点G，H, 且M，N分别为线段EF，GH的中点，若k1k2=-4，求证：直线MN经过一个定点.(参考答案：定点为(0，5).)

剖析：点P与抛物线的位置关系有三种：点在抛物线的内部、点在抛物线上和点在抛物线的外部.由①式可知：只要已知k1k2的值，直线MN必经过定点.变式中动点P的纵坐标不变，定点的坐标没有变化，目的是为了让学生发现变化中的不变，激发学生学习数学的兴趣.

3.2 由点到线，体系初现

思路2：循着从点与抛物线的位置关系到直线与抛物线的位置关系的研究路径，改变两条直线与抛物线的位置关系探究直线MN是否过定点.同时交换题目中的题设和结论的位置，可以得出新的定值问题，丰富定值结论.

图5

变式4如图5，直线y=k1x+b1和直线y=k2x+b2交于点P(t，3)(t<-3)，直线y=k1x+b1与抛物线y=x2-6交于点E，F，M为线段EF的中点，直线y=k2x+b2与此抛物线有唯一公共点N，且k1k2=-4，求证：直线MN经过一个定点.(参考答案：定点为(0，5).)

图6

变式5如图6，过点P(t，-8)的直线y=k1x+b1和直线y=k2x+b2分别与抛物线y=x2-6有唯一公共点M，N，求证：直线MN经过一个定点.(参考答案：定点为(0，-4).)

变式6如图6，过点(0，-5)的直线与抛物线y=x2-6交于点M，N，过点M，N分别作直线y=k1x+b1和直线y=k2x+b2与此抛物线均有唯一公共点，两直线交于点P，求证：(1)k1k2为定值；(2)点P在定直线上运动.(参考答案：(1)k1k2=-4；(2)点P在直线y=-7上运动.)

剖析：变式4和变式5分别得到了抛物线的切割线和双切线的图形，探究发现都存在着类似的定值问题.将变式5的条件和结论互换后得出变式6.类比圆幂定理，沿抛物线的相交弦→双割线→切割线→双切线这一主线进行变式探究，将整个定值问题串成一条线，进而形成一个网络，一个体系，让学生感悟知识和结论的统一美.

3.3 位似变换，奇异再现

思路3：将核心条件中M,N的位置由中点变为线段对应的三等分点、四等分点、五等分点……直至平移到分别与点F，H重合，探究直线MN是否经过定点.

图7

图8

变式8如图8，点P(-3，3)在抛物线y=x2-6上，直线PF:y=k1x+b1交此抛物线于另一点F，直线PH:y=k2x+b2交此抛物线于另一点H，若k1k2=-4，求证：直线FH经过一个定点.(参考答案：定点为(3,7).)

剖析：将直线MN平移，MN都经过定点，更为奇异的是，这些定点的坐标是有规律的，都在经过点P的一条射线上.通过推理和演示，让学生领略位似变换带来的数学的奇异美.

3.4 斜率关联，有律可寻

思路4：原题中两条直线的斜率相互关联，改变核心条件中两条直线的斜率之间的数量关系，又有怎样的定值问题？

变式9如图9，点P(-3，3)在抛物线y=x2-6上，直线PF:y=k1x+b1交此抛物线于另一点F，直线PH:y=k2x+b2交此抛物线于另一点H，且M，N分别为线段PF，PH的中点，若k1+k2=-4，求证：直线MN与经过原点的一条定直线平行.(参考答案：直线MN与直线y=2x平行.)

图9

图10

剖析：由①式可知直线MN的表达式与k1+k2和k1k2有关，那么当已知点P(a，b)时，改变k1和k2的数量关系就会出现三种定值问题：(1)若已知k1k2，则直线MN过y轴上一定点；(2)若已知k1+k2，则直线MN与定直线平行；(3)若k1k2和k1+k2满足一次函数关系，即k1k2=p(k1+k2)+q(p，q为常数，且p≠0)，则直线MN过非y轴上的一定点.

3.5 条件“隐形”，以形代数

思路5：引入垂直、等腰等几何“元素”,将斜率k1和k2之间的数量关系“隐形”，让学生借助几何直观来解决问题，借此体验由“形”到“数”的转化过程.

图11

图12

变式12如图12，点P(-3，3)在抛物线y=x2-6上，过点P的直线y=k1x+b1和直线y=k2x+b2分别与x轴交于点S，T，与此抛物线分别交于另一点F，H，且PS=PT，M，N分别为线段PF，PH的中点，求证：直线MN与经过原点的一条定直线平行.(参考答案：直线MN与直线y=6x平行.)

剖析：通过构造相似，将几何条件转化为线段之比，再将线段之比转化为k1和k2的关系，经过化简后发现变式11中的PH⊥PF可以转化为k1k2=-1，变式12中的PS=PT转化为k1+k2=0.这些知识的获得不是靠超前学习和死记硬背得到的,而是借助形的特殊位置及性质通过推理和计算得到的，这可以让学生更好地理解数学本质.

4 教学反思

4.1 有序变式，贵在自然

变式教学应遵循学生的认知规律，体现知识的发生、发展的过程，让学生的思维螺旋式上升.以母题为基础，从学生认知的最近发展区出发，有序改变问题中的核心条件和背景，由点与抛物线的位置关系变到直线与抛物线的位置关系，由相交弦→双割线→切割线→双切线，由特殊到一般，由简单到复杂，由单一到多样，由显性到隐性，目的是让学生发现变式的思路是有律可循的，明白变式的生成也是有源可寻的.学生在母题的演变过程中不仅体会到了变式的自然生成，而且对问题的解决和方法的领悟也不断深入.在潜移默化中,学生掌握了数学学习规律，提升了审美意识，形成有序思维、发散思维等良好思维品质.

4.2 变式之道，成于自主

苏霍姆林斯基认为，在人的心灵深处，都有一种根深蒂固的需要，这就是希望自己是一个发现者、研究者、探索者.教学中不能只让学生被动地解答变式问题，更要让学生主动地发现、提出问题变式.变式教学的最终目标是让学生做变式的主人.第一，通过变式教学，要厘清变式思路及其生成途径，要让学生知晓：(1)常见的变式策略和方法；(2)题目中有哪些核心条件，可以变什么，怎么变；(3)还能往哪变.第二，教学中要敢于放手，从简单问题入手，加强学生对变式问题解决的自我探索与合作探究,加强学生对变式提出和解决思维过程、思维策略与方法的感悟，加强学生对变式活动经验的概括、提炼与内化[2].第三，要用欣赏和鼓励的眼光去看待学生的变式成果，增强其自信心，激发其内驱力，最大限度地挖掘其潜能.

5 结束语

在变式中思考，在变式中提高，是变式的魅力之所在.教学中，要精选具有良好的“生长点”和“延伸点”的例题，通过变式教学促进学生养成自主变式、深度学习的习惯，不断提升其数学素养.