基于GA-BP神经网络的滑坡运动距离预测*

胡俊涛，张细香

(湖北省地质局第五地质大队，湖北 黄石 435004)

0 引言

滑坡是我国重大地质灾害之一，每年由此造成的经济损失巨大。对于水平运动不明显受阻的滑坡而言，滑坡的运动距离既受体积和高差的影响，也与地形坡度有关。虽然滑坡运动过程中可能存在较多的坡度变化，但坡脚型滑坡运动区和堆积区分界点的坡度差通常处于坡脚位置，且对滑坡运动的作用非常显著[1]。滑面平均坡度(α)、滑动区与堆积区的坡度差即坡脚角度(β)和堆积区平均坡度(γ)都会对滑坡运动距离产生较大影响。在我国西南山区，由于地形和地质构造的原因，由地震引起的坡脚型滑坡比较常见。滑坡运动距离是评估滑坡灾害的一项重要指标，对其进行合理预测能为当地的防灾减灾工作提供参考。

目前国内外学者针对滑坡运动提出了许多模型与理论，如多因素耦合机制、空气润滑机制以及能量传递机制等[2-4]。李秀珍等[5-7]通过定性与定量研究得出滑坡体体积、场地条件、地质构造是影响滑坡运动的重要因素。针对滑坡运动距离，唐然等[8]从动力学角度设计了模拟实验，推导了滑坡运动距离理论计算公式；樊晓一等[9-14]基于统计学原理，通过数值模拟和回归分析，得出了不同类型滑坡运动距离的预测方法，确立了各影响因素与滑坡运动距离之间的关系。但是由于滑坡的内在机理复杂，以上研究形成的方法和模型对于滑坡运动距离的预测精度还有待提高。近年来，神经网络因具有强大的非线性处理能力和自主学习特性，被广泛应用于各领域的预测问题研究，并取得了较好的预测效果[15-16]。然而，神经网络在滑坡问题的研究中应用较少。

本文通过主成分分析提取影响滑坡运动因素的主成分，剖析滑坡运动机理，再基于遗传算法优化的BP神经网络构建网络模型，以西南地区75个由地震引起的坡脚型滑坡为样本对该模型进行训练和测试，并以此模型对我国西南地区由地震引起的坡脚型滑坡运动距离进行预测。

1 研究区概况

本文选取的滑坡主要分布在汶川县东北部和茂县东南部地区，是汶川地震灾区的Ⅹ、Ⅵ度烈度区。该地区海拔较高且起伏较大，西部最高海拔超过了3 000 m，东部低至780 m，呈西高东低的地势。大部分区域都是山地，地质构造复杂，岩浆岩分布广，处于龙门山断裂带上，易发生地震，故由地震引起的滑坡比较常见。

2 研究方法

2.1 构建GA-BP神经网络模型

滑坡运动因具有较大危害而受到了广泛关注，由于内在机理复杂，传统统计学方法在预测运动距离时存在一定困难。人工神经网络是学者受生物神经网络感知世界的原理启发而提出的一种数学模型，具有强大的非线性问题处理能力，弥补了传统统计学方法的不足。BP神经网络是一种基于误差逆传播算法的多层前馈神经网络，其具有学习和自适应等特点，整个训练过程包括数据的正向传输和误差的反馈修正两个过程[17]。本文通过研究滑坡运动距离的影响因素，构建GA-BP神经网络预测模型，以此对地震引起的坡脚型滑坡运动距离进行预测。此外，将BP神经网络和GA-BP神经网络模型预测结果与回归预测结果进行对照，以验证神经网络相较于传统统计学方法在滑坡运动距离预测中的适用性。

2.1.1 BP神经网络基本结构

BP神经网络在训练时，数据通过输入层按权重传递到隐含层，经过非线性处理，最终作用到输出层，输出层通过误差反馈调节数据传递过程中的连接权重和阈值。典型的BP神经网络包含一个输入层、一个隐藏层和一个输出层，其拓扑结构如图1所示。

图1 BP神经网络拓扑结构

2.1.2 网络参数设定

隐藏层神经元层数与单层神经元数的确定对整个网络的性能有着显著影响，确定方法不唯一，采用式(1)初步确定隐藏层神经元数，可在实际训练过程中适当调整。神经网络中传递函数、学习算法和效率、初始阈值和权重的选取也可能会对整个网络的性能产生很大影响，在训练过程中根据结果确定合适的学习算法和效率，初始阈值和权重由遗传算法优化得到。

(1)

式中：N为隐藏层神经元数，m为输入层神经元数，n为输出层神经元数，t为0～10的整数。

2.1.3 遗传算法优化BP神经网络

BP神经网络具有强大的数据拟合预测能力，初始权重和阈值的确定对神经网络的性能具有较大影响。遗传算法优化BP神经网络的目的便是优化其初始权重和阈值，从而使BP神经网络能够更加科学快速地完成模型训练。遗传算法优化BP神经网络的要素包括种群初始化、适应度函数选择、选择操作、交叉操作和变异操作。具体的算法流程如图2所示。

遗传算法在搜索最优初始权重和阈值的过程中，确定合适的种群规模以及交叉变异概率，可使神经网络训练更快逼近极限最优解，避免陷入局部最优解和算法不收敛的情况发生。

图2 遗传优化BP神经网络算法流程

2.2 主成分分析

为了在网络模型的构建中更加充分地反映各因素之间的内在联系，提高预测模型的精度，利用Matlab2016对影响滑坡运动的因素做主成分分析，将得到的主成分作为神经网络的输入神经元。

2.2.1 分析各因素相关性

通过min-max法[见式(2)]对原始数据进行标准化处理，消除各个因素量纲带来的影响，利用Corrcoef函数求得各因素的相关系数矩阵，再对各因素做KMO和Bartlett检验，以此判断选取的因素是否适合做主成分分析。

(2)

2.2.2 主成分表达式

利用Matlab2016的PCA函数做相关性分析，得到特征值、主成分贡献率以及得分矩阵，从而得到主成分表达式：

Yi=X·Wi,

(3)

式中，Yi为第i个主成分，X为影响滑坡运动各因素组成的向量，Wi为第i个主成分的得分向量。

3 结果与分析

3.1 滑坡影响因素

影响坡脚型滑坡运动的主要因素有地质构造、岩性、地震等级、滑坡体含水率、滑坡体体积、坡度、地形起伏度、高程、归一化植被指数等。本研究选取的滑坡样本均为汶川地震引起的坡脚型滑坡，在该范围内的地质构造、岩性和滑坡体含水率比较接近，地震是滑坡的启动因子，因而震级不会影响滑坡体的后续运动情况，在构建模型时不考虑这4个因素。归一化植被指数与滑坡的发育相关性较低[18]，对滑坡运动距离影响较小，为了提高模型训练效率，在构建模型时将该因素舍去。根据相关研究[19-21]，最终确定6个因素作为研究指标：坡脚以上滑面长度L，滑面平均坡度α，坡脚角度β，堆积区平均坡度γ，滑坡体体积V，滑坡体前后缘高差H。

3.2 主成分分析结果

对确定的研究指标做主成分分析，得到相关系数矩阵(见表1)。由表1可知，大部分因素之间的相关性较高。对各因素做KMO和Bartlett检验得到KMO检验系数为0.606，大于0.5；Bartlett检验的Sig值为0.001，小于0.05。综上可知，选取的因素之间具有较强的相关性，适合做主成分分析。计算得到的公因子方差见表2。由表2可知，各因素的公因子方差均接近1.0，说明提取的主成分能较好地反映原始数据的信息。

由Matlab计算得到的特征值及主成分贡献率见表3。由表3可知，前3个主成分的累计方差贡献率达到了92.87%，主成分1、2、3的特征值分别为3.17、1.35、1.03，均大于1，说明这3个主成分能够充分反映各因素对滑坡运动距离的影响。主成分得分矩阵见表4，由此得到3个主成分的表达式：

(4)

(5)

(6)

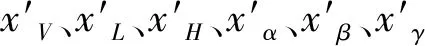
由式(4)-式(6)可以看出，滑坡体体积(V)、坡脚以上滑面长度(L)、滑坡体高差(H)都在第一主成分Y1上有较大的载荷，体现了滑坡体在加速阶段能量的积累能力，可称之为动能因子；滑面平均坡度(α)和坡脚角度(β)在第二主成分Y2上有较大载荷，体现了滑坡体在加速阶段的加速能力，可称之为加速因子；坡脚角度(β)和堆积区平均坡度(γ)在第三主成分Y3上有较大载荷，体现了滑坡体过渡到减速阶段的能量损失情况，可以称之为阻力因子。

表1 相关系数矩阵

表2 公因子方差

表3 特征值及主成分贡献率

表4 主成分得分矩阵

3.3 网络模型预测与分析

通过试验最终确定遗传的种群规模为20，进化次数为50，交叉概率为0.4，变异概率为0.2，网络学习效率为0.1，目标误差为0.01，以此构建由地震引起的坡脚型滑坡运动距离预测模型。试验过程中，从样本总体中随机抽取60个样本作为网络模型的训练集，其余的15个样本数据作为测试集。采用绝对误差(AE)、相对误差(APE)和平均相对误差(MAPE)3个指标来评价预测结果的准确性，其计算公式分别为

EAE=abs(LP-Lmax)，

(7)

(8)

(9)

式中：EAE为预测的绝对误差，m；EAPE为预测的相对误差，量纲为1；EMAPE为预测的平均相对误差，量纲为1；LP为模型的预测值，m；Lmax为模型的期望值，m；n为测试集的容量，量纲为1。

为了验证在此类问题中，神经网络相较于传统数理统计方法的先进性以及遗传算法对BP神经网络的优化能力，在主成分分析的基础上，采用最小二乘法进行多元回归分析，并分别用多元回归、BP神经网络(BPNN)及GA-BP神经网络对滑坡运动距离进行预测。最大垂直运动距离H和最大水平运动距离L的回归方程见式(10)、式(11)，各方法预测结果分别见表5、表6。

由表5、表6可知，GA-BP神经网络对滑坡运动距离的预测效果最好，垂直和水平方向运动距离最小绝对误差分别为1.16 m和1.01 m，最小相对误差分别为0.74%和0.54%，相对误差低于10%的样本分别占了测试样本的93.33%和86.67%，绝对误差的标准差分别为4.87和5.91，GA-BP神经网络预测的准确度和稳定性均优于多元回归和BP神经网络(BPNN)预测。

H=58.83+0.38Y1-0.39Y2+1.44Y3。

(10)

L=-184.15-0.85Y1+2.42Y2+4.26Y3，

(11)

表5 垂直运动距离预测误差

表6 水平运动距离预测误差

4 结论

本文首先通过主成分分析提取了影响坡脚型滑坡运动距离的主成分，再基于遗传算法优化的BP神经网络构建了坡脚型滑坡运动距离的预测模型，对坡脚型滑坡运动距离进行了预测，取得了较好的预测效果，并将神经网络模型预测结果与多元回归预测结果进行了对比，得到以下主要结论：

a.构建的GA-BP神经网络模型对滑坡运动距离预测结果精确且稳定，其强大的非线性问题处理能力适合用于解决内在机理复杂的滑坡运动问题。

b.GA-BP神经网络模型在预测的精确性和稳定性方面均优于原始BP神经网络模型，说明遗传算法从网络的训练过程到结果输出都对BP神经网络进行了较大优化。

c.对于滑坡运动距离的预测精度，GA-BP神经网络最优，其次是BP神经网络，基于多元回归预测的偏差较大且不稳定，效果最差，说明神经网络相较于传统数理统计方法更适用于该类问题的研究。

利用GA-BP神经网络构建滑坡运动距离预测模型，是将人工智能与实际工程相结合的一次尝试，为该类研究引入了新方法和新思路，对我国西南地区由地震引起的坡脚型滑坡的影响范围和灾害强度的预测具有现实意义。本文仅选取了我国西南地区由地震引起的坡脚型滑坡运动作为研究对象，而滑坡运动的影响因素与内在机理非常复杂，在研究过程中发现，滑坡运动距离预测模型的建立还受滑坡的规模区间影响，后续将对此作进一步研究。