基于超同步轨道的GEO目标天基近实时探测方法
2022-08-22张洪波武冠群王典军胡伟赵辰
张洪波 武冠群 王典军 胡伟 赵辰
(北京空间飞行器总体设计部,北京 100094)
近年来,随着各国航天活动的飞速发展,产生了数量庞大的空间碎片,这些空间碎片引起的碰撞和解体风险日益增大,成为人类航天活动的公害,给各国空间活动带来了越来越大的现实威胁[1]。为了尽可能对碰撞和解体等空间事件进行预警、规避和防护,各国对空间态势感知和空间安全的需求愈发迫切,美国、英国等国家先后制定并发布了国家空间安全政策,综合运用各种手段确保本国空间生存安全与发展安全[2-3]。
空间态势感知作为开展各类空间活动的基础能力,已经引起各国高度关注和投入[4-5]。空间态势感知是空间安全的基础,旨在尽可能彻底地描述在陆地环境和太空领域运行的太空能力,确保空间操作与空间飞行安全,保护太空能力和国家利益等,主要分为探测与识别、告警与评估、特征描述、数据集成与利用等。其中,空间目标探测与识别是指搜索、发现和跟踪目标,对空间目标和事件进行探测,辨别空间目标类别[6],是空间态势感知的数据来源,也是获取未来空间优势的重要保证,已成为优先发展领域。
地球同步轨道(GEO)是高价值太空资产最集中、轨道资源最宝贵的区域,自然成为空间态势感知的重点和空间安全防护的热点,对地球同步轨道空间目标探测的重访频度要求越来越高,近实时探测需求日趋迫切。美国正研究构建天地一体化的空间目标探测与识别系统,在地面升级部署多频段雷达系统,发展新型空间探测望远镜(SST)等光学设备;针对地球同步轨道目标,美国在低轨部署天基空间监视系统-1(SBSS-1)及作战响应空间-5(ORS-5)卫星等,进行目标探测与识别,同时部署地球同步轨道空间态势感知计划(GSSAP)星座,以抵近识别和侦察地球同步轨道目标。俄罗斯也在积极发展国际科学光学观测网(ISON)等大型地面光学设备网,完善对地球同步轨道目标的探测识别能力[6-9]。传统的低轨卫星观测同步轨道、同步轨道卫星观测同步轨道的观测方式,均存在长时间侧逆光观测问题,无法满足近实时要求。超同步轨道卫星的轨道高度高于GEO,可对GEO目标长时间顺光观测,是解决近实时探测的理想途径。
本文对球体和方体两种典型空间目标的视星等和有效反射面积进行了分析,提出了基于超同步轨道的天基近实时探测系统轨道部署策略,并完成效能仿真分析。
1 球体目标视星等分析
天基光学系统通过接收空间目标反射的太阳照射光进行探测,视星等是对空间目标反射太阳照射光而产生的亮度的度量。从天基系统观测空间目标的视星等为[10]
(1)
式中:-26.74为天基系统观测太阳的视星等;i为空间目标可见面元的数量;σi为面元漫反射系数;Sim为单个面元有效反射面积;R为目标与天基系统距离。
由式(1)可见,空间目标视星等取决于目标外表面漫反射系数σi、有效反射面积Sim和目标与天基系统距离R。漫反射系数σi取决于目标外表面材料属性,为常数,本文统一取0.3。距离R取决于目标与天基系统运行轨道。有效反射面积Sim是指目标受太阳照射的有效面积在观测方向上的投影[11]。
有效反射面积Sim的计算方法为
Sim=S·cosα·cosβ
(2)
式中:S为面元面积;α为阳光入射方向与面元法线的夹角,定义为入射角;β为观测方向与面元法线的夹角,定义为反射角;将α与β之和定义为光照角。如图1所示。

图1 面元有效反射面积计算
可见在面元面积固定的情况下,有效反射面积受光照角影响,即当太阳、空间目标和天基探测系统三者相对位置变化时,有效反射面积和目标视星等随之发生变化。近实时探测需要分析视星等全周期的变化,确保视星等最差时仍在天基系统探测能力范围之内。
球体模型多用于自然天体视星等分析,或作为标准空间目标评估不同天基探测系统效能,也可用于部分卫星球面部分(如天线反射面等)的视星等分析。
如图2所示,由于球体表面各部分入射角、反射角不同,采用积分方式求解等效面积Sm。在目标球体中心建立右手坐标系OXYZ,单位面元dS与+Z轴夹角为φ,面元在XOY面上投影与+X轴夹角为ω,则有
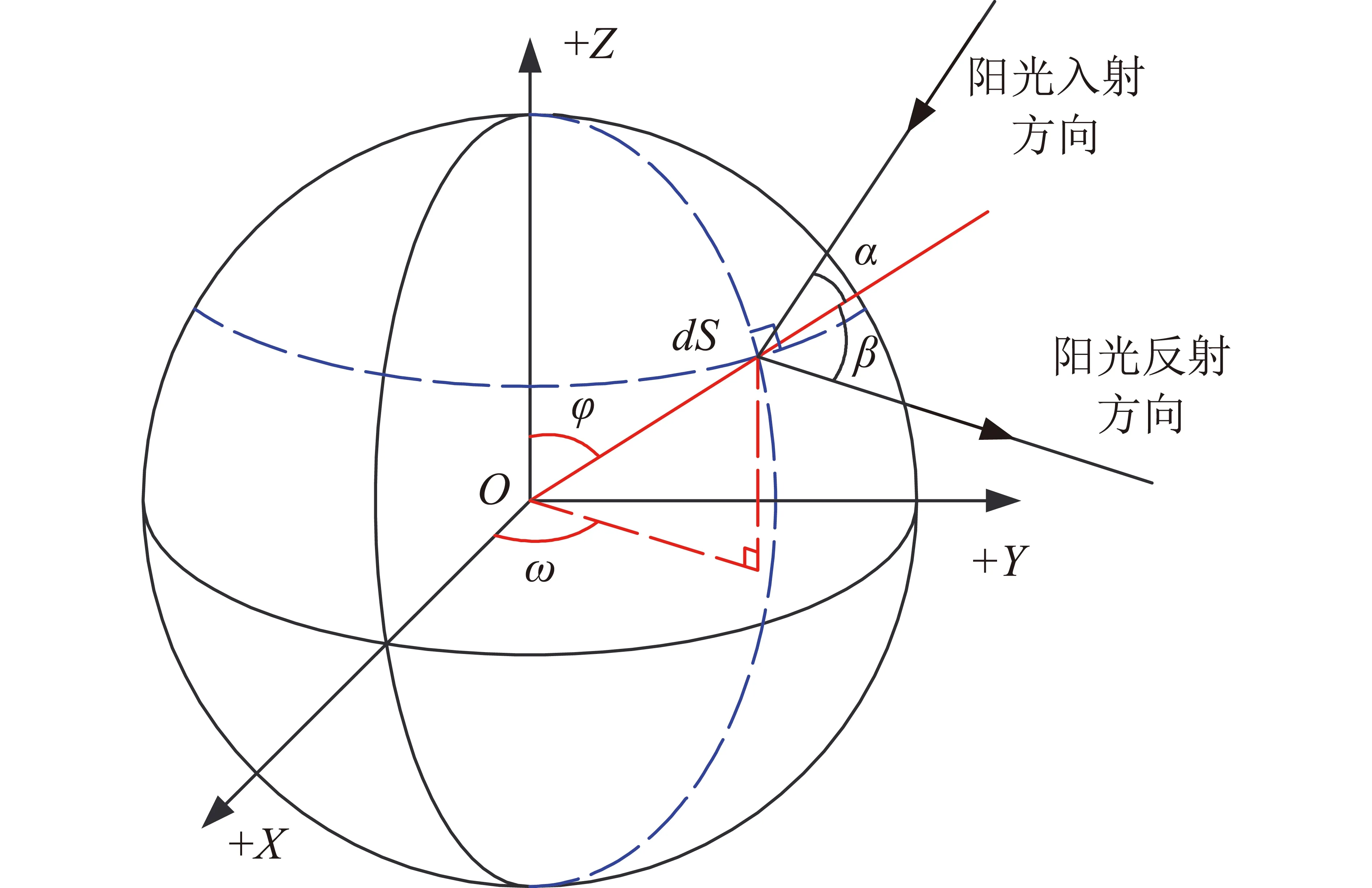
图2 球体目标有效反射面积计算
dSm=dS·cosα·cosβ=(R·dφ)·
(R·sinφ·dω)·cosα·cosβ
(3)
对整个球面进行积分,可得
(4)
根据式(4),直径1 m的球体有效反射面积随光照角变化曲线如图3所示。由于光照角在180°~360°之间变化规律与0°~180°之间变化完全对称,图3只给出0°~180°计算结果。
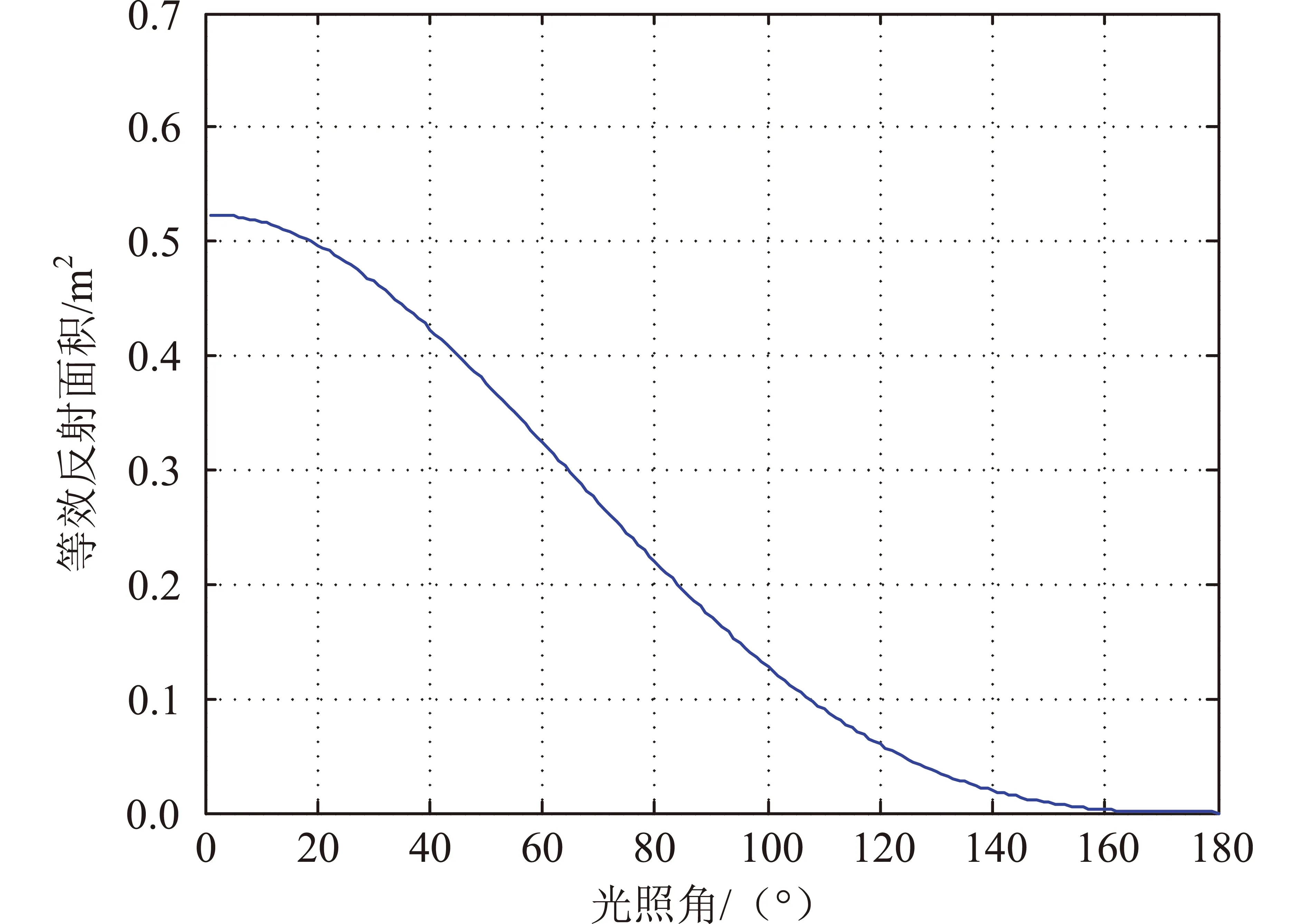
图3 直径1 m的球体目标有效反射面积随光照角变化
可以进一步求得目标对于天基探测系统的视星等,距离分别取10 000 km、20 000 km、60 000 km、80 000 km和110 000 km,计算结果如图4所示。
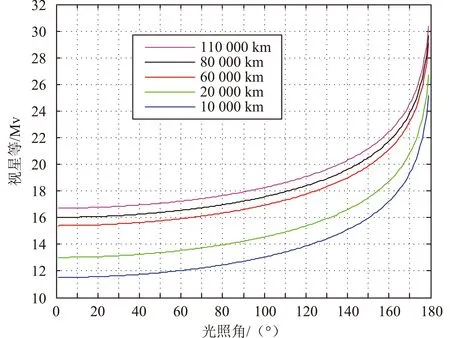
图4 直径1 m的球体目标视星等随光照角变化
由上述分析结果可知,对于球体目标,光照角、有效反射面积、视星等关系如下:
(1)光照角为0°时,有效反射面积最大,为0.523 6 m2,为球体横截面积的66.7%。
(2)光照角为0°~180°变化时,有效反射面积随光照角增加而减小,光照角为60°时,有效反射面积为最大值的61.9%,光照角为90°时,有效反射面积为最大值的32.7%,光照角为120°时,有效反射面积为最大值的11.4%,光照角为150°时,有效反射面积为最大值的1.6%。
(3)除光照角为180°的情况外,其余情况目标均可见,即有效反射面积不为零,视星等不为无限大。
(4)光照角大于90°后,目标视星等加速升高,探测难度增大。典型结果为距离80 000 km,光照角为80°,视星等为17 Mv。
2 方体目标视星等分析
方体目标视星等与目标姿态有关,由于卫星±Y面一般用于散热,受照较少,本文仅针对±X和±Z面受照情况开展分析。与球体目标不同,方体目标姿态对有效反射面积产生影响:当光照角<90°时,可以观测到一个受照面或两个受照面;当光照角≥90°时,只能观测到一个受照面,如图5所示。
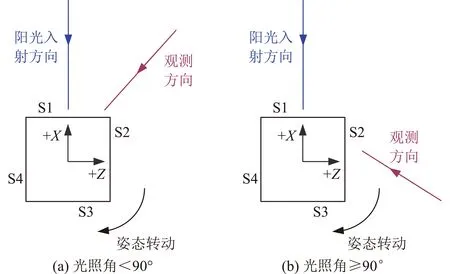
图5 方体目标的视星等计算
设定目标位边长1 m的立方体,使目标绕+Y轴旋转角度,可以得到不同光照角情况下有效反射面积与姿态旋转角的关系如图6所示。
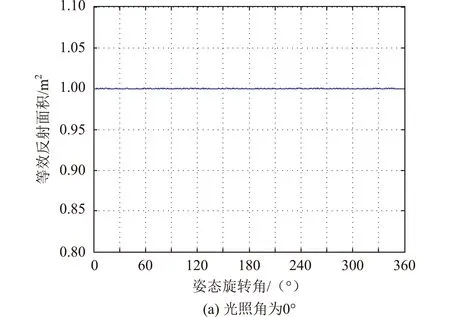
图6 边长1 m立方体目标等效反射面积随姿态变化
由上述分析结果可知,对于方体目标,光照角、等效反射面积关系如下:
(1)不同光照角约束下,等效反射面积在一定区间内波动,光照角越大,平均等效反射面积越小;
(2)与球体目标不同,当光照角≥90°时,出现等效反射面积为0的区域,即不可见区域;
(3)在光照角一定时,等效反射面积在入射角与反射角相等,二者均等于光照角一半时出现极大值;
(4)当光照角一定时,等效反射面积在以下两种情况会出现极小值,即第一种为入射角为0°,第二种为反射角为0°(光照角<90°)或反射角为90°(光照角≥90°)。
3 GEO目标隐蔽姿态及特性分析
方体目标等效反射面积出现极小值,即同等条件下的视星等最低,意味着可以最大限度避免被发现,出现情况可以归纳为方体目标的某个面正对太阳或正对天基探测系统。由于天基探测系统方位不易确定,目标可以选择某个面正对太阳作为隐蔽姿态。如果此时目标正处于地球和太阳之间,则高轨、低轨的天基探测系统对其观测的光照角均>90°,等效反射面积为零,无法发现目标,此时正值白天,地基光学系统无法发挥作用,于是目标实现完全光学隐身。这种盲区场景持续时间可长达几个小时,足以发生空间安全事件,是天基近实时探测需要解决的最恶劣的极端工况,后文均将方体目标按照此种姿态分析。
当方体目标处于隐蔽姿态时,距离分别取10 000 km、20 000 km、60 000 km、80 000 km和110 000 km时,计算得到目标视星等如图7所示,结果表明:

图7 边长1 m立方体目标视星等随光照角变化
(1)存在一半时间的不可见区域,需要两颗探测卫星实现全天近实时探测;
(2)光照角超过80°后视星等急剧升高,光照角达90°时视星等接近无限大。
根据GEO目标隐蔽姿态及其特性分析结果,为了实现对其长时间的近实时观测,需要观测系统具备以下条件:
(1)观测光照角不应超过80°,以保证目标具备可观测的视星等;
(2)采用超同步轨道。当目标运行到地日之间时,低轨、中轨、同步轨道卫星对其观测光照角均>90°,无法观测,因此需采用超同步轨道,保证顺光观测;
(3)多星组网观测。根据超同步轨道与GEO相对运动关系,单星无法一直保持在对GEO目标顺光观测位置,因此需要多星组网观测,观测卫星数量根据观测GEO带范围的需求确定。
4 探测轨道设计及效能
本文提出一种观测我国国土上空GEO带的观测系统轨道部署策略,由两颗卫星组成,双星采用周期为47 h44 min18 s的圆轨道,半长轴66 809.6 km,偏心率0,卫星对于相同地理经度的星下点回归周期为48 h,回归地方时均相同,即双星隔天在UTC时间05:40:00(95°E地方时12:00)星下点地理经度为95°E,目标为探测我国国土上空GEO带。
探测效能分析的目的,是分析出双星探测系统能够进行近实时探测的地球同步轨道带经度范围。仿真时两颗卫星倾角19.5°、升交点赤经0°、近地点幅角0°、真近点角10.8°和190.8°。以边长为1 m的立方体作为分析目标,目标始终保持一个面对日,即同等条件下的隐蔽最低视星等姿态。选取目标的定点经度由10°E~180°E之间变化,分析两颗探测卫星在48 h内观测目标的视星等,二者视星等取较小值即为对探测卫星相机的视星等性能要求。
图8给出了95°E、120°E、16°E和174°E等典型轨位目标的视星等分析结果。结果表明:
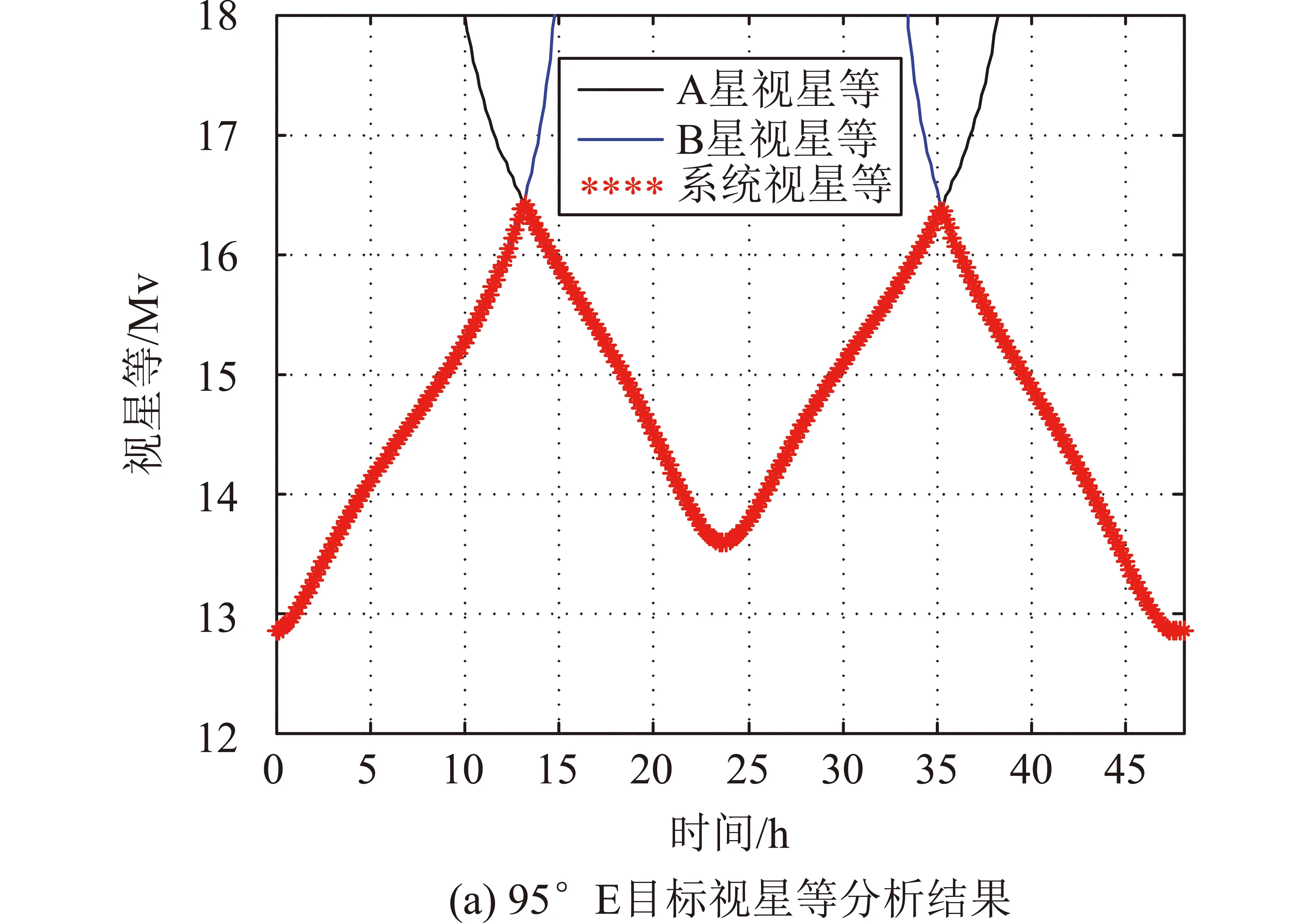
图8 典型轨位目标的视星等分析结果
(1)当目标位于95°E附近时,目标对探测卫星的视星等不超过16 Mv;
(2)目标轨位距离95°E越远,目标对探测卫星的视星等逐渐增大;
(3)可以实现158°(16°E~174°E)范围内边长1 m方体目标的全天近实时探测,即95°E±79°,基本可以覆盖我国国土上空地球同步轨道带。
5 工程可行性分析
5.1 轨道稳定性分析
利用STK软件建立仿真场景,如图9所示,仿真起始时间为UTC 2021年4月10日05:40:00,两颗卫星星下点地理经度分别为95°E和85°W,星下点地方时分别为12:00和0:00。即两颗卫星星下点经过95°E时,其星下点地方时均为12:00,95°E为可近实时探测区域的中心。
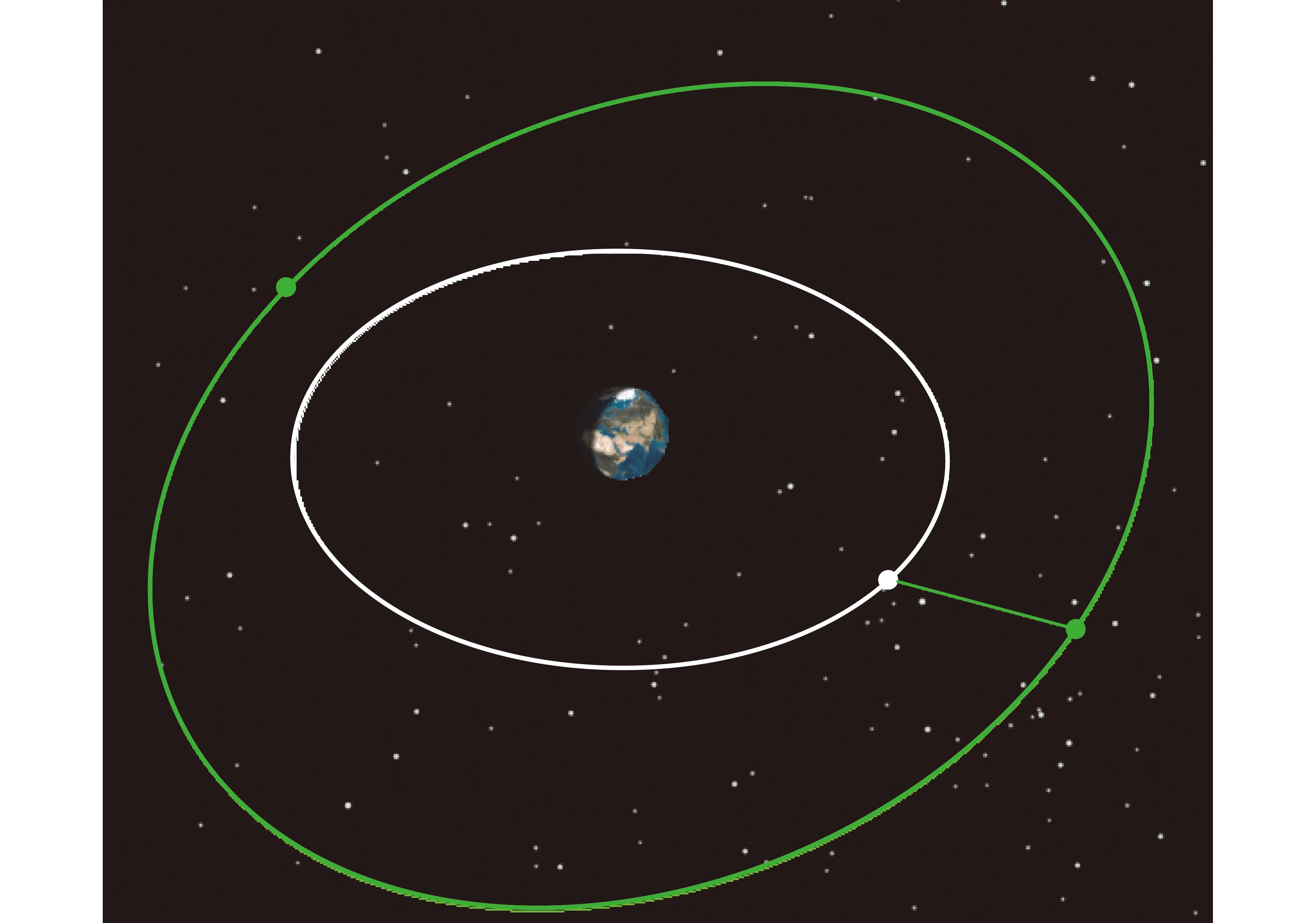
图9 轨道部署策略
图10为两颗卫星在1年中每隔1天UTC时间05:40:00(95°E地方时12:00)星下点地理经度变化情况,变化范围不大且呈现明显周期性变化,进行少量相位调整后可以使95°E星下点回归周期稳定在48 h左右,可以保持轨道稳定。
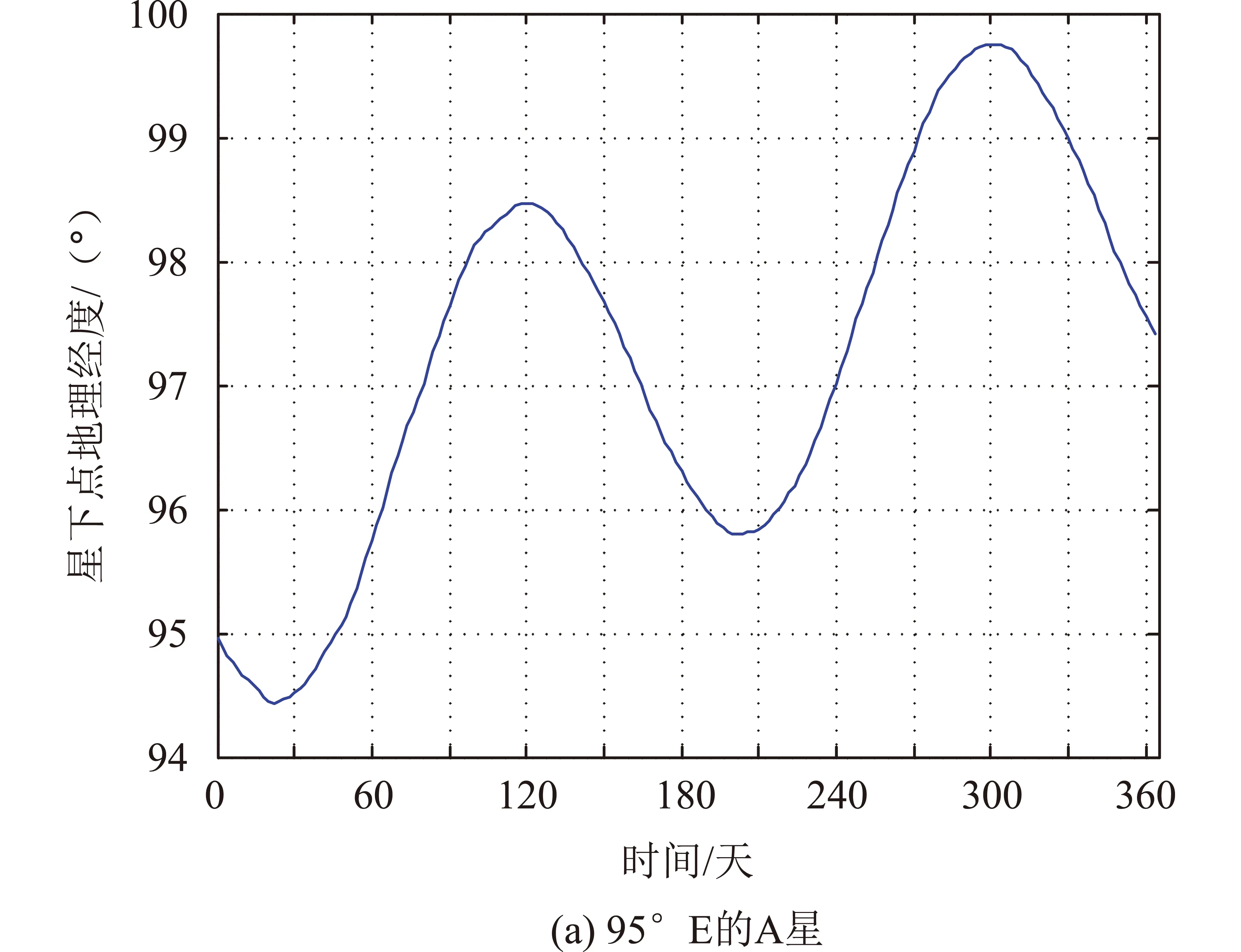
图10 两颗探测卫星间隔48 h星下点地理经度变化情况
5.2 地球干扰影响分析
天基探测卫星观测地球同步轨道带目标时,存在地球进入相机视场的情况,将引起相机饱和无法成像,需要进行地球干扰的影响分析。天基探测卫星所处轨道高度对于地球的半张角为±5.5°,本文将目标至探测卫星、地球至探测卫星两个矢量组成的夹角定义为干扰角,如干扰角≤5.5°,则地球产生干扰。
因天基探测卫星存在轨道倾角,当卫星经过升降交点时,地球干扰范围最大、持续时间最长。经分析,受扰范围星下点经度差最大为7°,仅占全部可观测范围的4.4%,如图11所示;受扰目标最长不可见时间仅为43 min,如图12所示,对于高轨目标异动和空间事件观测和分析可接受。
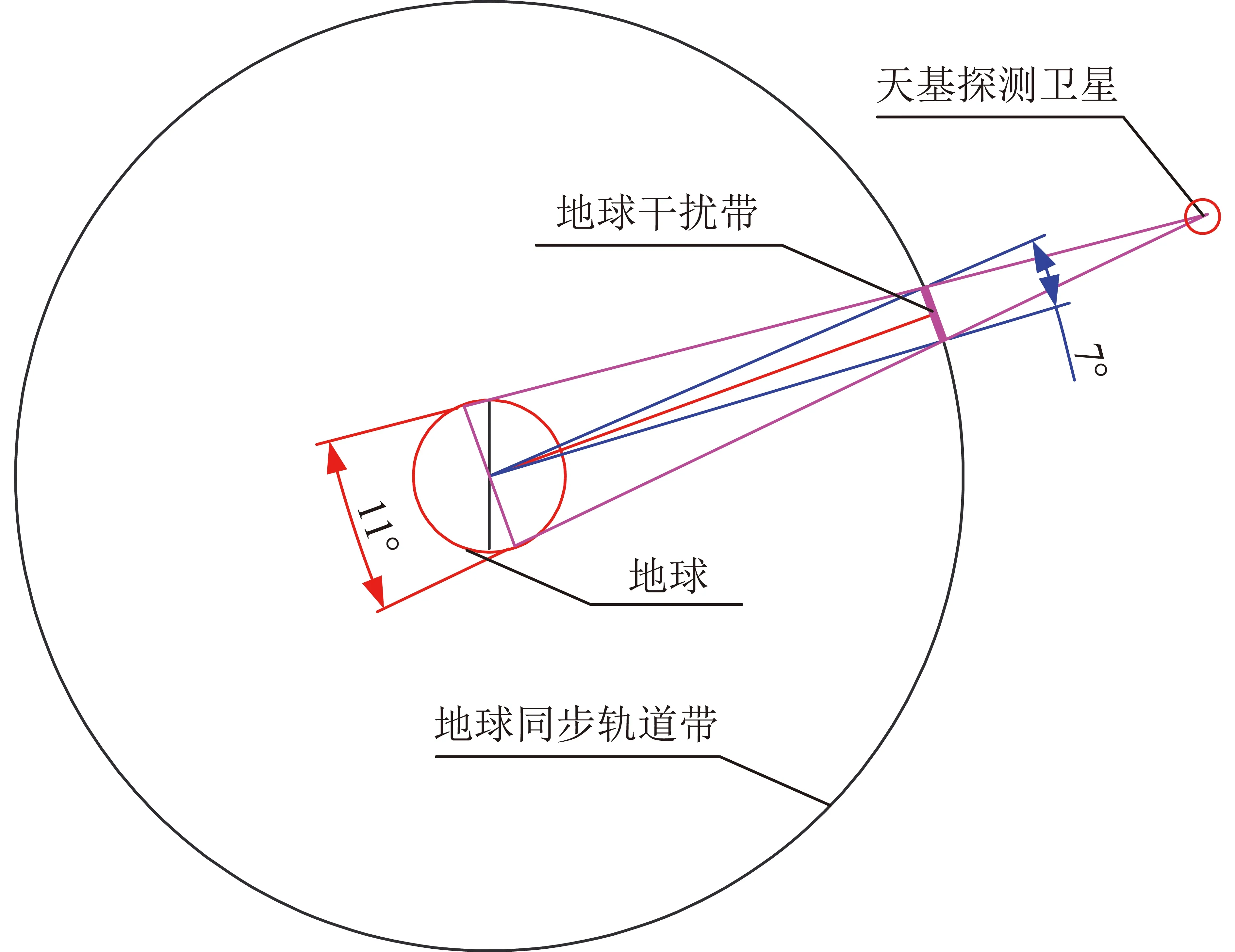
图11 地球干扰影响分析

图12 典型工况地球干扰影响时长分析
6 结束语
随着地球同步轨道带空间活动的日趋增加,对其高重访探测需求越来越大。本文通过对球体和方体目标视星等分析方法的研究,总结出光照角对视星等影响,提出并分析了方体目标隐蔽姿态,针对方体目标隐身场景,提出了基于超同步轨道的GEO目标天基近实时探测方法,双星组网即可对我国国土上空实现近实时探测,卫星轨道稳定性好,探测受地球干扰影响小,具备较好的工程可行性,对未来我国天基空间目标探测领域发展具有一定的参考意义。
