三角图的原理、快速绘制以及在砂岩分类中的应用

单云鹏，王红军，张良杰，白振华，苏朋辉，赫英旭，孟维康，刘航宇，程木伟

1.中国石油勘探开发研究院，北京 100083

2.中海石油（中国）有限公司天津分公司渤海石油研究院，天津 300459

3.中海油能源发展股份有限公司工程技术分公司，天津 300452

4.北京大学地球与空间科学学院，北京 100871

0 引言

三角图的散点分类效果显著，三角图中某一点三个组分含量之和为1 或100%，一般某个点距离最近的角，其所对应的组分所占权重较大，可以快速直观表述受三个影响因素事物的相似程度及分类结果。三角图在各学科中已有普遍应用[1-7]，如地理科学中工厂选址的三个影响因素比重：市场需求、交通运输以及矿产资源；有机地球化学中判断沉积环境的三环萜烷指标[8]：C19+20TT、C21TT 与C23TT，判断油气来源的C27-C28-C29规则甾烷[9-12]；无机地球化学中判断玄武岩成因的指标[13]：MnO、TiO2与P2O5；地质学中判别岩石的各种矿物组分[14-18]，砂岩类型的三端元组成：石英、长石与岩屑[19-22]等。但由于各专业特点不同，三角图内部的区域划分以及投点读值方法不尽相同，本研究仅关注三角图最广泛的用法以及在砂岩分类中的应用。

砂岩的分类方案众多，Krynine[23]在1948 年提出第一个普遍应用的砂岩三端元分类体系，三端元分别为：石英+硅质岩（代表成分成熟度）；长石+高岭石（代表母岩性质）；云母+绿泥石（代表构造变动强度），这个分类体系仅注重沉积岩中的矿物组分，而没有考虑沉积岩中不可忽略的岩屑组分，不管是从科学角度，还是油气田实际应用出发，今天都不再适用。随后Gilbert[24]在1954 年引入“杂砂岩”与“净砂岩”的概念，形成了“三端元四组分”划分方案的理论雏形，在进行砂与砂岩分类之前，先依据杂基含量将其划分开，杂基小于15%的为“净砂岩”，杂基大于15%的为“杂砂岩”。同年，Folk[25]提出一个三角图砂岩分类方案，三端元分别为：石英+燧石（代表沉积来源）；长石+岩浆岩屑（代表火成来源）；云母+变质岩屑（代表变质来源）。1964 年Dott[26]根据Gilbert 引入的概念，以棱柱图的方式进行表示，兼顾了成分成熟度与结构成熟度的表达，三端元分别为石英+“燧石类”；长石；不稳定碎屑。其中，燧石类包括如去玻化的酸性玻璃等硅质火山物质，显然，这种并非稳定的硅质火山碎屑与稳定石英划分为一组是有失妥当的。1968 年，Folk[27]对自己提出的三角图进行了修改，将燧石归入到岩屑单元，以石英作为三角形单独的一个端元，另外两个单元为长石+火成岩屑+片麻岩屑以及其它岩屑+燧石。Folk 的砂岩分类强调结构成熟度概念，需要依据砂岩中黏土含量、颗粒磨圆以及分选性等，将砂岩结构成熟度划分为若干等级。曾允孚、夏文杰在1986 年的主编的《沉积岩石学》教材中，在总结了前人研究以及1978 年成都地质学院（现成都理工大学）岩石教研室编制的砂岩分类方案的基础上提出一种三端元四组分分类方案，与Dott相同，使用棱柱图的方式进行表达，杂基含量作为棱柱，反映细砂级以上砂岩的水动力作用，三端元分别为：石英（代表成分成熟度）；长石（代表深层来源）；岩屑（代表表层来源），其中岩屑包括燧石、石英岩以及其它硅质岩屑。因为燧石和石英岩的耐磨性与化学稳定性与石英相比，还是弱一些，并且成分成熟度高的海滩相中，燧石与硅质碎屑少见，故燧石等成分归于岩屑比较合理。其中三端元的三角图，为目前国内各大油气田常用的砂岩分类三角图，即是本文探讨制作的重点。这种分类方案分区数目适中，且属于脆性矿物的石英、长石含量分别作为单独的端元，在致密砂岩这类非常规储层评价中[28-29]依然适用，体现了该分类方案的优势。本文在阐述了前人的疏漏以及三角图的基本原理后，以同一组数据分别利用Excel、Origin 以及Grapher 绘制三角图进行相互验证与对比。并采用对计算机运行环境要求相对较低的VBA 编程分别提供国内油气田常用的，以及划分更加详细的砂岩分类图版。

1 两种形态划分与读值规则

一般来讲，三角图最常呈现的形状为等边三角形；在国内，各大油气田与高校最常用的砂岩分类三角图则是底边与底边上的高长度相等的等腰三角形[30-40]，而这种特殊的等腰三角形在形态上与等边三角形十分相似，在尺度较小的时候难以分辨其形态，加上分类图版中会添加一些辅助线，导致科研人员忽略了这两者的区别，造成了三角图概念与使用不清晰的情况。

等边三角形有三个坐标轴，读值是以三角形的每条边作为一个做坐标轴，如图1a，每一个坐标轴代表一个组分的含量由0～100%，常以逆时针方向增大。判断其中某一点A的数值，通过A点分别做三角图三条边的平行线，取三条平行线增大的方向与三角图边的交点为A点该组分的含量。

等腰三角形读值以底边上的高为Y 轴，含量为0～100%；以与平行于底边的三角图内部的某一条线段为X 轴，含量为0～100%。判断其中某一点B 的数值，如图1b，首先读取其Y值，这个Y值为B点的石英（Q）组分在石英+长石+岩屑中的含量；再通过B点做与底边平行的线段，分别交两条边于B1和B2点，B1与B2两点分别代表0 与100%，而这条边上的数值代表岩屑（R）组分在长石+岩屑中的百分含量。而理论上不同的砂岩样品中石英的含量有无数个数值，所以线段B1B2的位置就有无数个可能，即等腰三角形中有无数个X轴。

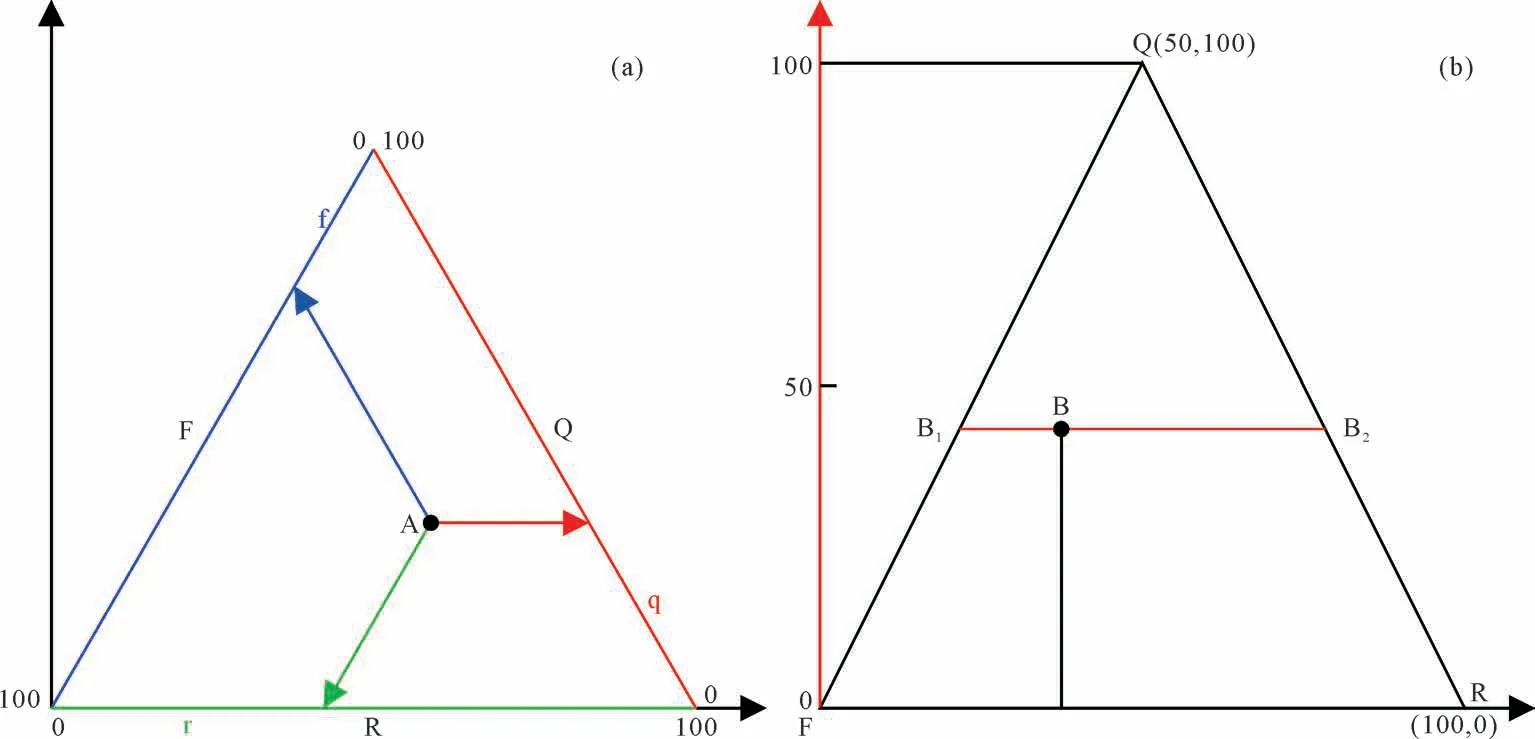
图1 两种三角形态与读值规则图Fig.1 Two types of triangle shape plots and reading rules

2 投点规则

由于两种三角形的读值规则不同，必然其相应的投点规则也就不同。实际上就是将三组数据（X，Y，Z）相加等于100%的数据经过不同的公式变换，形成在直角坐标系中的两组数据（X，Y）进行投点。前人有过高引用率的探索和推导[41-42]，但遗憾的是，文献[42]中等边三角形与等腰三角形的推导都具有逻辑性错误，下面将对前人的错误进行论证。

2.1 前人错误的证明

为方便读者进行考证对比，图2中关键的交点命名、直线命名以及各矿物含量的取值符号将与文献[42]中的图2保持完全一致，进行推导和证明，并在表1 中将推导过程中的错误点进行总结。图2 中两种三角形的F点与坐标系的原点重合，底边与坐标系的横坐标重合，即取点F（0，0）、R（100，0），在等边三角形 中 取Q（50，50），在等腰三角形中取Q（50，100）。

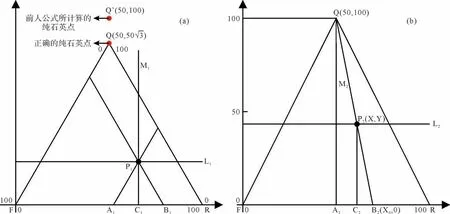
图2 前人使用的推导图（据文献[42]修改）Fig.2 Derivation plots used by predecessors (modified from reference [42])

2.1.1 等边三角形的错误

文中虽然在等边三角形推导的开始的描述阶段，规定了三条边长度相等，即QF=FR=RQ=100，见图2a，但是在其“直线方程推导原理”以及“相似三角形推导原理”的推导过程中，第一步就将P1点的纵坐标推导为Y=P1C1=Q，出发点就出现错误。假设极端情况下，某砂岩样品长石F 与岩屑R 的含量为0，石英Q 的含量为100%，这一点在三角图中应该是三角形的石英顶点Q；而按照文中的投点公式，这一点横坐标值为50，坐标值为Y=100，见图2a点Q’，三边长度均为100 的等边三角形，底边上的高仅仅为()/2×100，该点在三角图中的投点已经溢出三角形的范围。也就是说，这种推导仍然是按照底边=底边上的高=100的等腰三角形进行的，已经不是等边三角形，而造成这种推导错误的原因是没有正确认识两种三角形图版读值的本质区别。

2.1.2 等腰三角形的错误

首先是直线方程的推导，如图2b，直线L2为经过等腰三角形中任意一点P2（X，Y）的平行于底边的直线，直线L2的解析方程为Y=Q，即P2点纵坐标为这一点的石英含量QP2；经过P2点与Q点的直线M2与底边相交于B2，B2的坐标值为（X0，0），作者根据投点规则，推导：

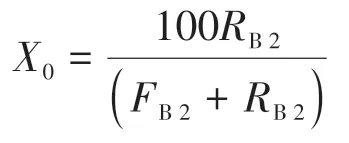
再通过B2（X0，0）与Q（50，100）以两点式的方式列出来M2的直线方程：

表1 前人推导过程中的错误总结Table 1 Summary of errors in previous derivations

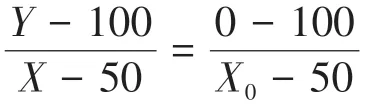
由于要求取的是直线M2上P2点的横坐标值，则代入Y=QP2可得

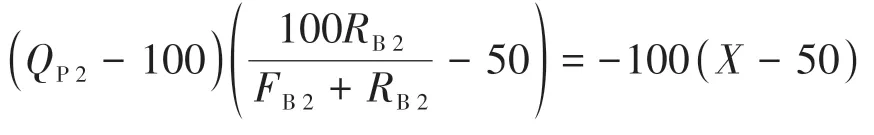
又由于各个点的三端元组分相加均为100，所以QP2-100=-（FP2+RP2），即X的取值方程化简为：

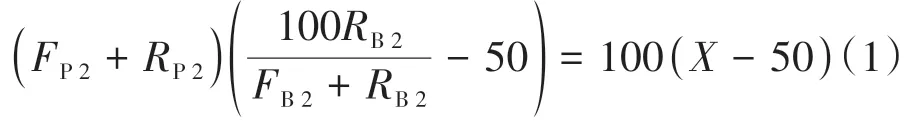
由于P2点与B2点石英含量是不同的，所以两点的长石与岩屑的含量之和一定是不相等的，即

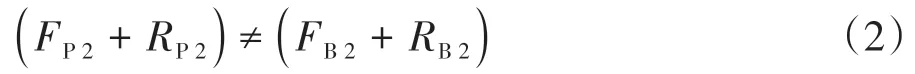
求取P2点横坐标的方程无法继续进行化简。但在文中，作者忽略了P2点与B2点的差别，当隐去（1）式中两点的下标，继续推导，就可以得到

接下来是相似三角形的推导，如图2（b），C2点为过等腰三角形中任意一点P2（X，Y）做底边的垂线，与底边的交点。可知P2点的横纵坐标值为

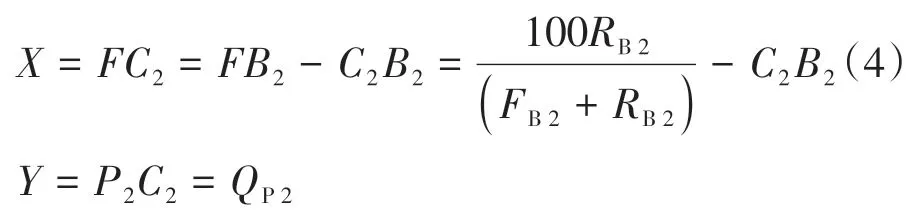
由于△P2C2B2∽△QA2B2，则

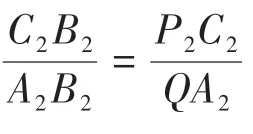
可得

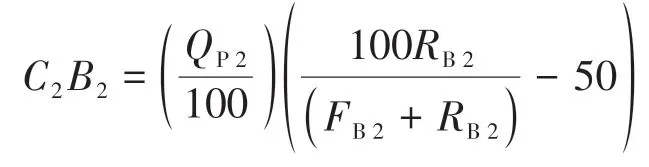
即

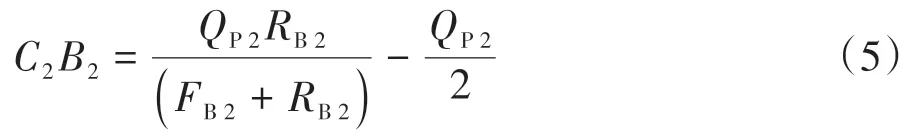
将方程（5）代入到方程（4）中得

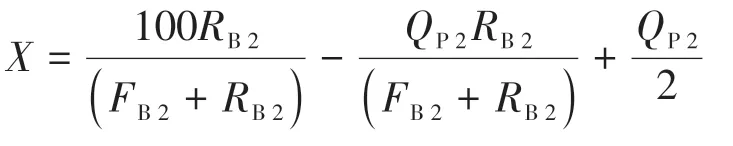
即

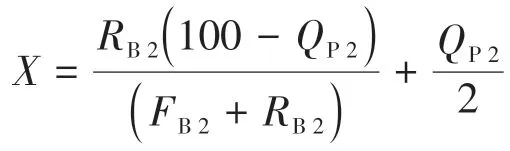
由于任意一点的三端元组分之和为100，则

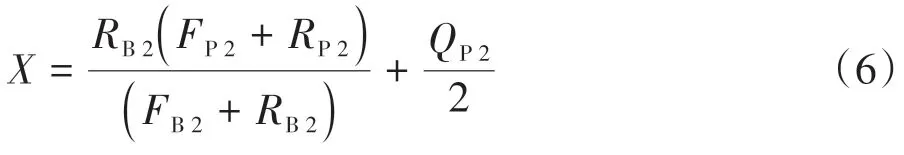
由于方程（2）的存在，方程（6）无法再继续进行化简。而在文中，作者仍然忽略两点石英含量不同的差别，可以看到，在隐去两点下标，方程（6）即可化简为方程（3）。

在等腰三角形中的推导中，由于其坐标转换的结论是“正确”的，很多读者会忽略这看似正确的推导过程，而没有注意到其中的逻辑性错误。

2.2 等边三角形投点规则

首先规定三条边的顶点分别为QFR，使F点做为直角坐标系的原点，如图3a所示，等边△QFR的三条边长度分别为100，按照逆时针方向增大，底边代表岩屑（R）含量，右侧边代表石英（Q）含量，左侧边代表长石（F）含量。经过三角形中任意一点A，分别做三条边的平行线，且经过A 点做X 轴的垂线，交点分别标在图中，三个组分的数值分别为石英（Q）：RG=q；长石（F）：EQ=f；岩屑（R）：FB=r。

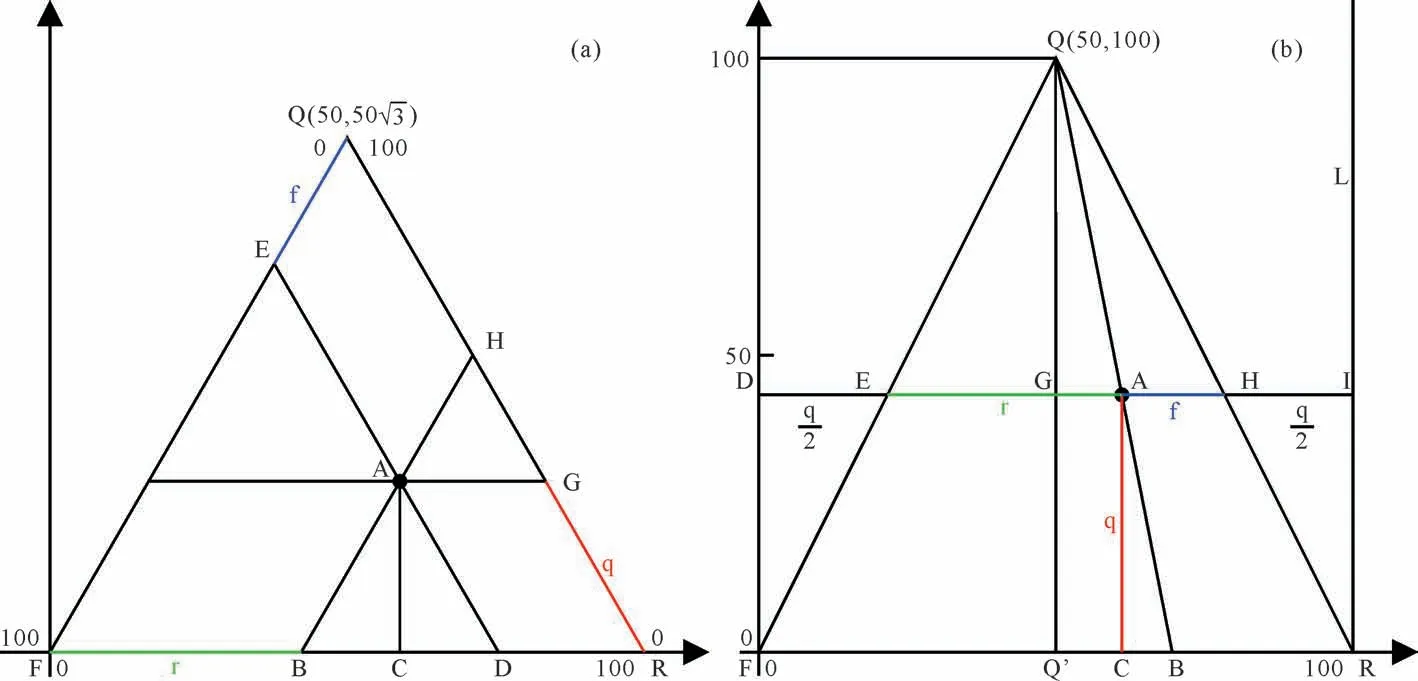
图3 两种三角形投点原理图Fig.3 Projection principle plots for two triangles

推导X 值：由平面几何关系，易知AD=GR=q，又△ABD为等边三角形，则

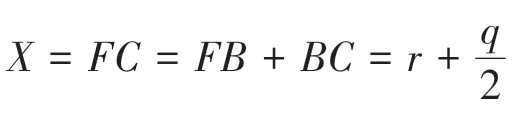
推导Y值：△ABD是边长为q的等边三角形，则

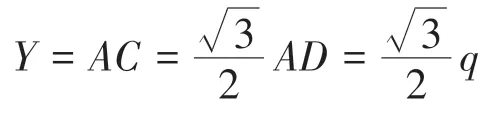
2.3 等腰三角形投点规则

建立直角坐标系，定点F（0，0），Q（50，100），R（100，0），规定等腰三角形三条边的顶点分别为QFR，QF=QR 为腰，过Q 点做底边FR 的垂线，交于Q’，如图3b所示，可知FR=QQ’=100。经过三角形中任意一点A，连接QA，并延长至FR 边，与FR 边交于B点；经过A点做FR边的垂线，与FR边交于C点；过R 点做Y 轴的平行线L，经过A 点做FR 边的平行线，与Y 轴、两条侧边、QQ’以及L 分别交于D、E、G、H、I点；三个组分的数值分别为石英（Q）∶q；长石（F）∶f；岩屑（R）∶r。

对于A点，坐标系的Y轴即为其Y轴，直线EH即为其X 轴，EA 在EH 上的长度占比代表岩屑组分在岩屑+长石组分中的百分比。

推导Y值：由投点规则易知，A点的纵坐标值Y=AC=q；

推导X值：

GQ’=AC=q，则QG=100-q；又△QFR∽△QEH，且QFR 为底边与底边上的高相等的等腰三角形，所以EH=QG=100-q；

又DE+EH+HI=DI，且DI=FR=100，则DE+HI=100-EH=q；

且△DEF≌△IHR，DE=IH，则

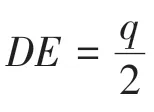
由读值规则知

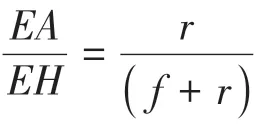
又由于EH=100-q，且q+f+r=100，即EH=f+r；则

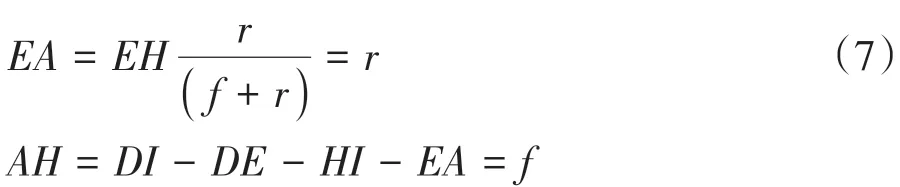
最终可得

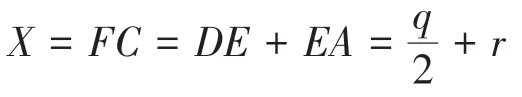
至此，可以证明，等边三角形与等腰三角形在坐标转换时的横坐标转换公式相同，均为X=r+q/2，但这其中却反应着不同的读值思维，有质的差别。且可以发现，线段EA、AH、AC的绝对长度，分别为A点岩屑、长石、石英的含量，可以使用三条线段的绝对长度快速读值判断三端元的含量。

3 图版建立

等边三角形的三角图没有特别的图版，一般为方便读值，作图者会在三角形内部画出分别与三条边平行的辅助线，如图4a。

对于等腰三角形，国内油气田常用的图版会划分出r/（f+r）=25%，r/（f+r）=50%，r/（f+r）=75%三条辅助线，分别对应r/f=1∶3，r/f=1∶1，r/f=3∶1，这几条辅助线不都呈特殊的角度，下面证明划分出来的区域符合砂岩分类的区间要求：

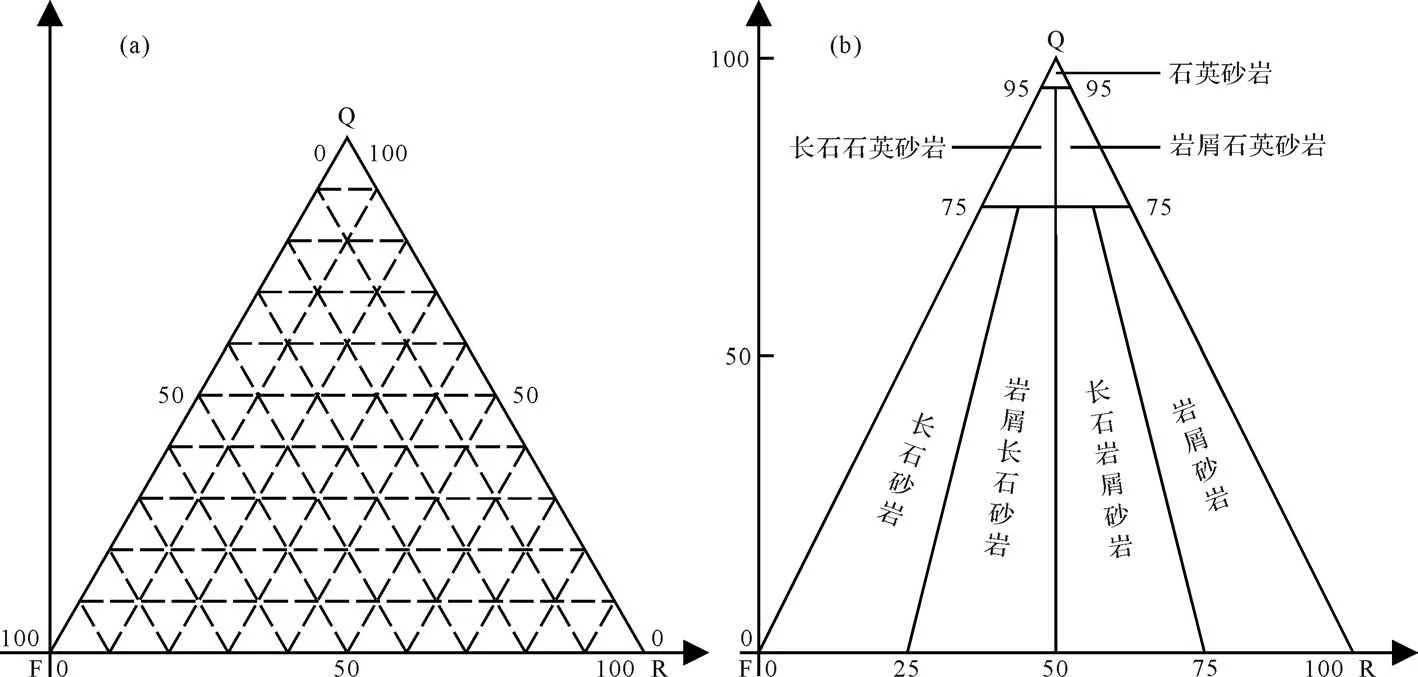
图4 等边三角形及国内油田常用三角图版Fig.4 Equilateral triangle plot and plot commonly applied in domestic oilfields

在图3b中，△QEA∽△QFB；△QAH∽△QBR；则

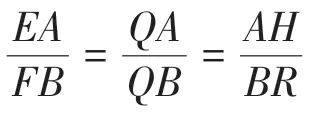
设EA=m，AH=n，FB=M，BR=N，EA/FB=QA/QB=AH/BR=α；可知

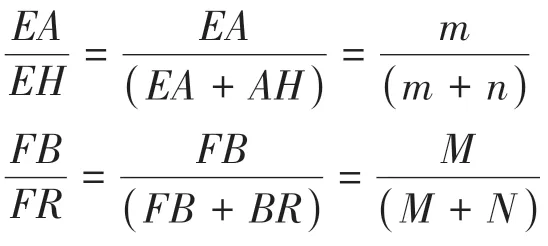
又m=αM且n=αN，则可以推出：

公式（8）说明等腰三角形内经过顶点Q 的与底边FR相交的任意一条直线上的点的岩屑在其长石+岩屑的组分中的含量百分比是相等的，即这条直线上的所有点，其r/（f+r）或r/f都是相等的。

在等腰三角形中，连接Q点与FR边上的25%与75%两点，并截去石英含量q＞75%以上的部分；通过Q 点做FR 边上的垂线，并截去石英含量q＞95%以上的部分，即是国内油气田最常用的砂岩分类图版，如图4b。

4 等边三角形的进阶拓展应用

4.1 “两边一高”砂岩分类图版

在明确两种三角形的读值与投点规则后，可以将两种三角形的思维结合起来使用。朱筱敏主编的《沉积岩石学》教材（2008）中，倡导了一种在华东石油学院（现中国石油大学（华东））于1975年编制的砂岩分类方案基础上改进的分类方案，如图5a，虽然使用广泛程度不如等腰三角形，但近年来也有学者在使用[43-44]，这种三角图使用了3个坐标轴，可将其形象地称为“两边一高”砂岩分类三角图。其投点与读值规则仍为等边三角形的相应规则，但进行了一些等价变换。在图5b中，梯形QFBH为等腰梯形，即QH=FB=r，以QF边作为判断长石含量的坐标轴，以QR边作为判断岩屑含量的坐标轴，将底边FR上的高QQ’作为判断石英含量的坐标轴，AD=GR=q，由于△ADC∽△QRQ’，则AD/QR=AC/QQ’，可知AC 在QQ’中的所占百分比即为石英的含量，即

为读值方便，可以把将QQ’看做100%，AC 相对于QQ’的长度为石英的含量q。等边三角形的投点是按照绝对长度进行的，而石英的读值则是取的AC边在QQ’边上的相对占比，这也是前人推导出现错误的原因。

4.2 “三边一高”砂岩分类图版

另外，文献[45-47]使用了文献[48]提出的砂岩分类方案，如图6a，这种分类方式相对来讲是最复杂的一种，一共使用了4 个坐标轴，可以称为“三边一高”砂岩分类三角图，投点与读值规则仍为等边三角形的规则。与图5b 的变换规则相似，见图6b，以QF 边作为判断长石含量的坐标轴，以QR边作为判断岩屑含量的坐标轴，将底边FR上的高QQ’作为判断石英含量的坐标轴；对于三角形内任意一点A，连接QA并延长至FR 边与FR 边交于B 点；通过A 点做FR 边的垂线，交于C点；通过A点做三条边的平行线，与三边的交点如图6b 所示，由等边三角形的平面几何关系，易知EA=r，AH=f，与等腰三角形的公式（7）相同；继续借鉴公式（8）的证明过程，可以说明直线QB 上的点，其r/（f+r）的值或者r 与f 的相对比例关系是相同的。在图6a中，连接Q在FR边上的25%与75%两点，分别截去f＜25%与r＜25%的部分；通过Q点做FR边上的垂线，截去q＞90%的部分以及50%＜q＜75%的部分，即是“三边一高”砂岩分类图版。

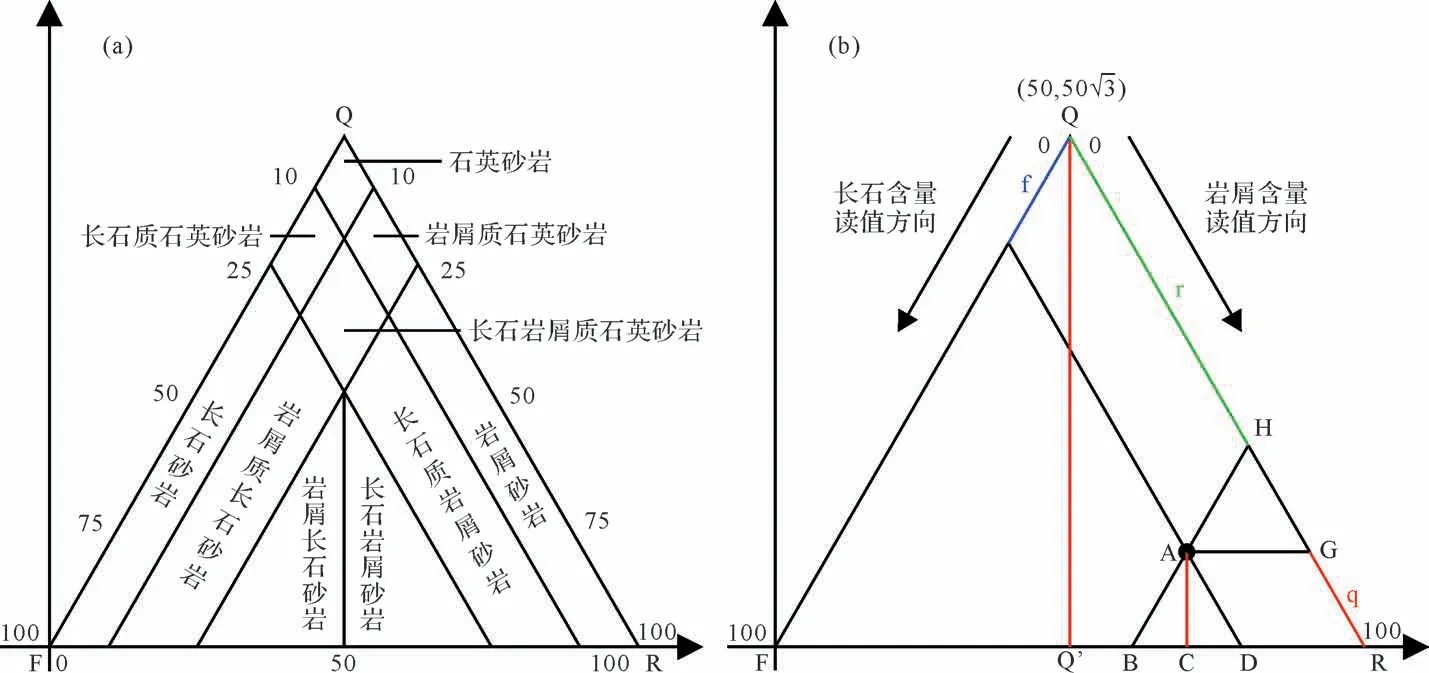
图5 “两边一高”砂岩分类三角图Fig.5 Ternary plots for sandstone classification with two side axes and one high axis

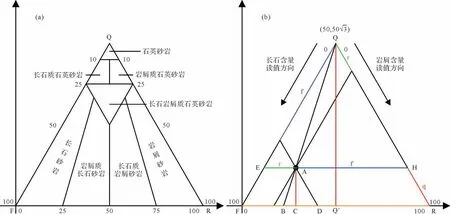
图6 “三边一高”砂岩分类三角图Fig.6 Ternary plots of sandstone classification with three side axes and one high axis

5 实例验证与作图对比

5.1 Excel作图

当将图7a 中的纵向坐标系重新分配，以Q 点的纵坐标高度为100，即为图7b。这里需要注意的是，图7b中是按照等腰三角形的投点经过拉伸压缩变换成等边三角形的，成为等边三角形后，其三条边的绝对长度代表三端元组分的含量；某一点纵向的绝对长度并不是石英的含量，而其在纵向坐标轴上的占比才是石英的含量，即公式（9）所表达的含义。

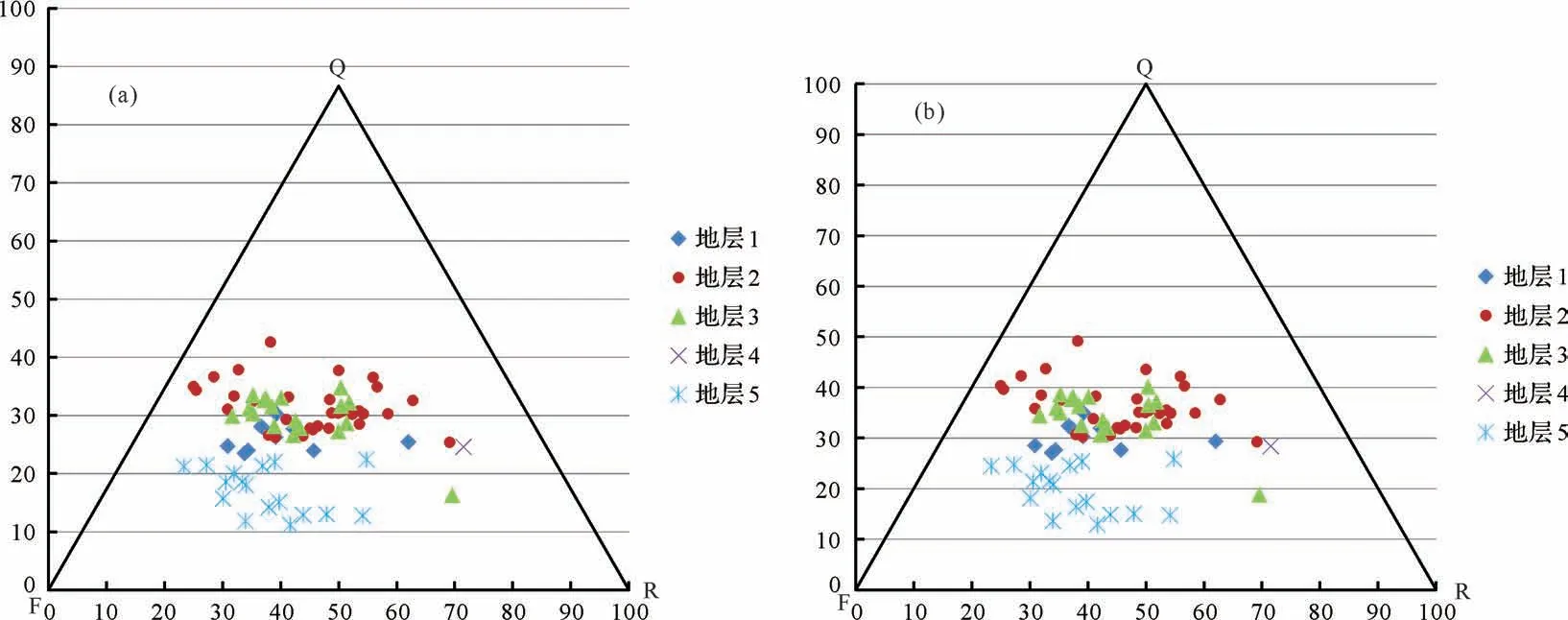
图7 Excel 绘制等边三角形Fig.7 Mapping equilateral triangles using Excel

在两类三角形图版中分别添加表2 中的国内油田常用砂岩分类图版中的辅助线，经过拉伸压缩变换，可以分别形成等边三角形砂岩分类图版以及等腰三角形砂岩分类图版。由图7可知，不管采用哪种投点方式，三角形形态均可以相互转化。为方便对比，直接取等腰三角形的投点方式进行调整成图（图8）。可以看到，两个图版的投点分类结果是一致的，在图4b划分出来的各个区域中，图8a与图8b完全相同，而不同的是它们的读值规则与相应的坐标轴，图8a 的读值规则遵循传统等边三角形的规则，三条边即为坐标轴，通过某一点分别作三条边的平行线进行读值；图8b 遵循等腰三角形的规则，并且经过2.3节的推导，某一点的高值为石英含量，通过这点与x轴平行且与三角形侧边相交的线段，以该点为分界点，左右两条线段分别为岩屑、长石的含量。而使用者在应用的过程中，有时没有明确区分两类三角形的形状，需要读者们自行注意两类三角形的读值区别。并且，笔者提倡在使用国内油田常用的砂岩分类图版时，采用等腰三角形的方式，因为等腰三角形的读值规则为水平或垂直的方式，更符合传统直角坐标系的使用习惯；而等边三角形的读值规则中，石英、长石、岩屑的读值分别需要采用0°、120°、60°的线段进行辅助，在实际使用中，不够直观。

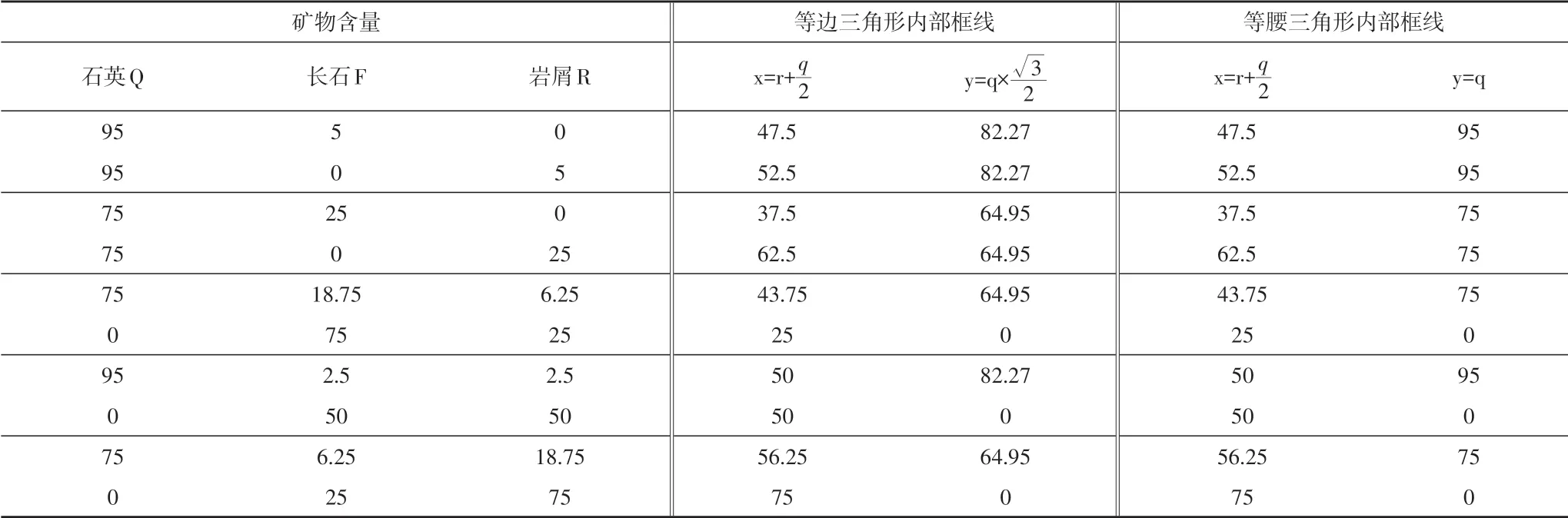
表2 国内油田常用的砂岩分类图版中辅助线节点坐标Table 2 Coordinates of auxiliary line nodes in sandstone classification charts commonly used in domestic oilfields

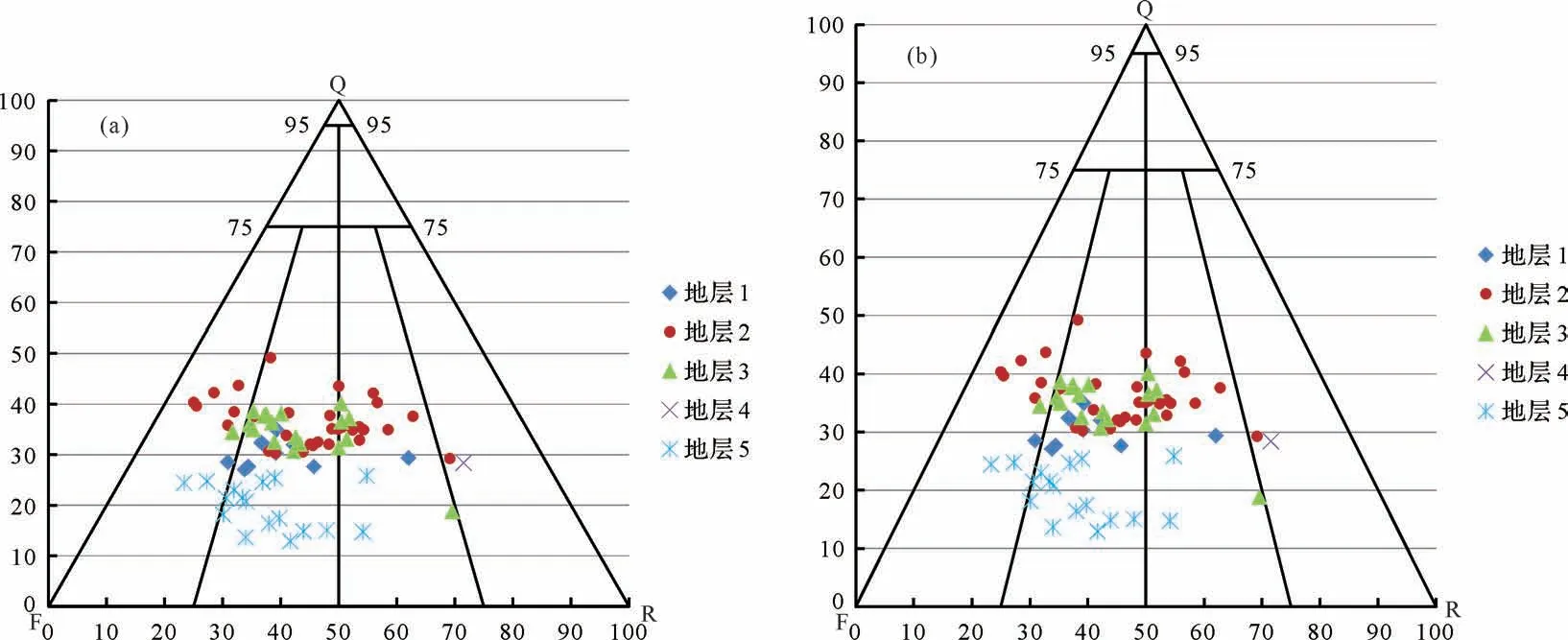
图8 Excel 绘制国内油田常用的等边三角形和等腰三角形两类图版Fig.8 Mapping equilateral and isosceles ternary plots using Excel, commonly used in domestic oilfields

5.2 Origin与Grapher作图

使用同一组数据，分别使用Origin 与Grapher 软件进行三角图绘制，如图9 所示。可以看到，绘制出的三角图与Excel的成图完全一致，虽然无法知晓这两种软件的后台程序代码，但可以确定其投点方式与理论推导出来的方程一致，无论是用等边三角形的方程还是等腰三角形的方程投点，三条边的坐标轴都是要经过均一化的处理，保持三条边的绝对长度相等。

两款软件的成图优点就是快速便捷。描述碎屑岩的矿物顺序一般为“石英—长石—岩屑”，这种排序会出图错误。需要注意的操作问题是Origin 在成图前，先要设置好三条轴，即岩屑为x 轴、石英为y轴、长石为z 轴；而Grapher 是在成图后，重新设置并对应坐标轴。

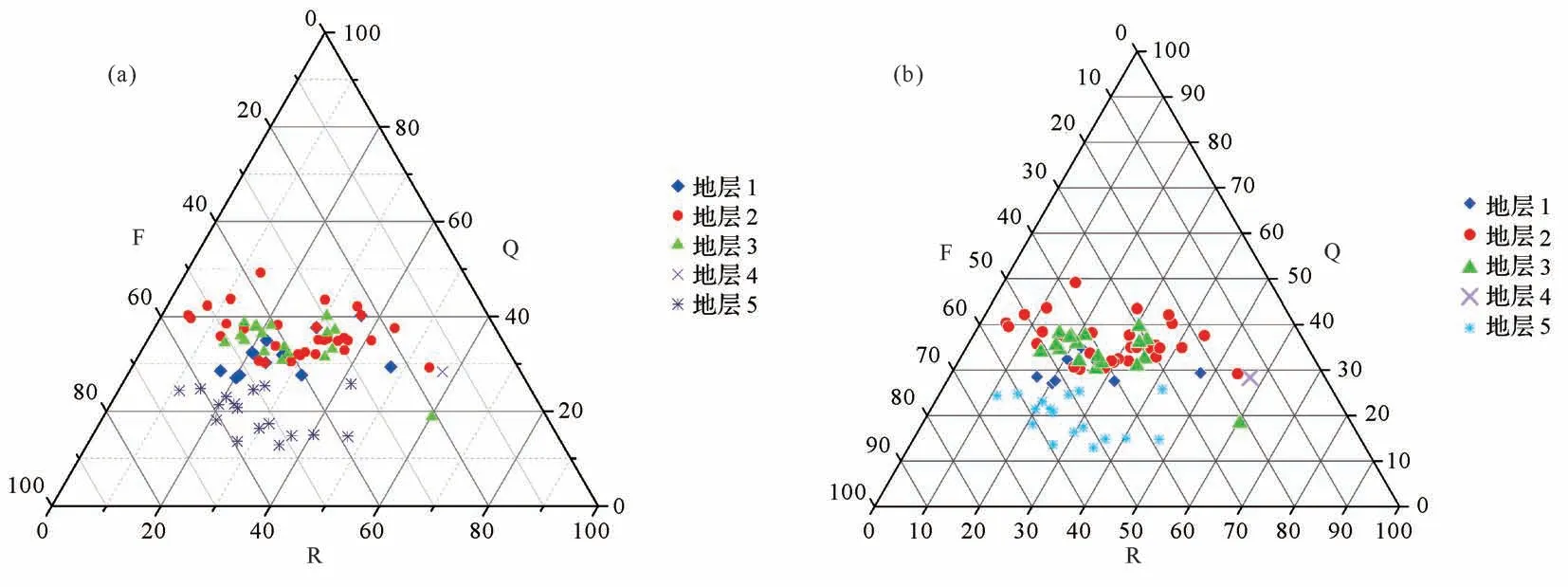
图9 Origin（a）与Grapher（b）三角图对比Fig.9 Comparison of (a) Origin, and (b) Grapher ternary plots

软件成图的缺点是只能按照设定好的模板对三角图内部平行于三条边的辅助线进行调整，各种地质图所需要的内部框线无法在软件中直接绘制出来；两款软件中的三角图不能实现不等比例的拉伸变换，其三角图只能保持等边三角形的状态，无法根据实际需要自定义三角形的形态。

6 分类图版及操作过程

6.1 手动生成图版

为计算方便，采用等腰三角形的计算投点方式，对每个点的x 与y 值进行计算。按照（100，0）、（0，0）、（50，100）、（100，0）的顺序在Excel 中插入“带直线的散点图”，即可生成三角形边框。分别以两点为一组的方式添加表2 中等腰三角形的内部框线或表3 中“三边一高”三角图的内部框线，可形成“国内常用”或“三边一高”砂岩分类图版。在图版中按照地层顺序添加矿物含量数据点，拉伸调整好三角形的形态，复制矢量图，在CorelDraw 中进行辅助信息的添加，即可完成砂岩的分类投点。

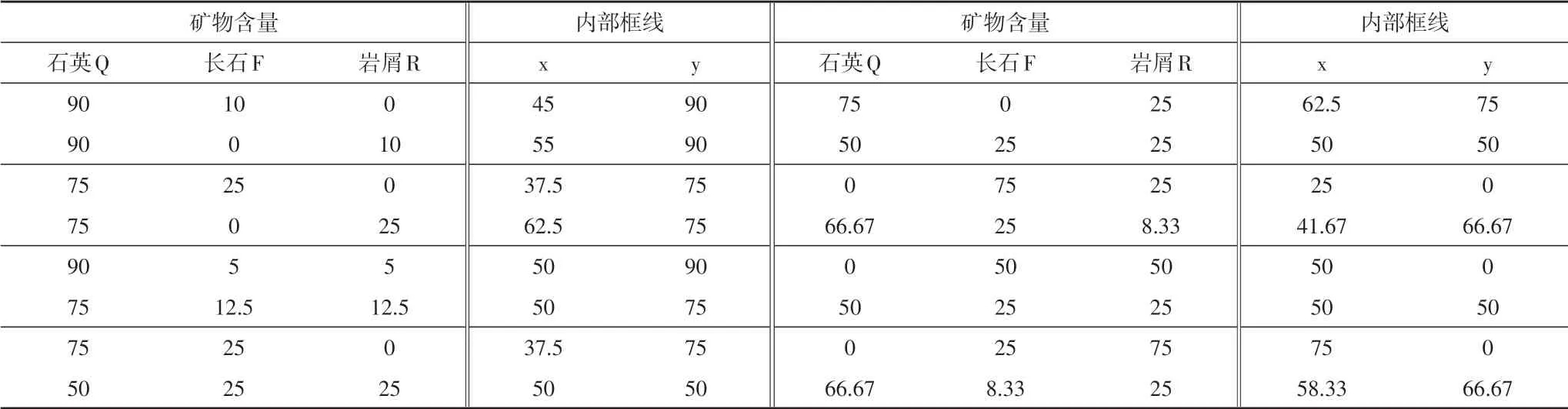
表3 “三边一高”砂岩图版中内部框线Table 3 Node coordinates of the inner frame lines in the“three sides and one height”sandstone plot

如前所述，“国内常用”图版既可以是等腰，也可以是等边的形态，读值规则会有差别，但“三边一高”图版应保持等边三角形的形态，因为其两条侧边在读值时起到坐标轴的作用。

6.2 自动生成图版

当需要反复多次进行三角图绘制，手动绘制工作量较大，为方便作图者快速完成砂岩分类工作，笔者对“国内常用”以及划分更为详细的“三边一高”砂岩分类图版进行了VBA 编程，两类图版代码将在国家冰川冻土沙漠科学数据中心发表，读者下载后可以直接复制运行，快速绘制。

本代码适用于准备采用“国内常用”或“三边一高”图版进行分类的砂岩地层，且各个散点已经按照石英+长石+岩屑=100%的规则将砂岩的三端元组分数据进行归一化处理，分类目的既可以是通过砂岩类型的变化来表征某一体系域内水动力的变化，也可以是常规的砂岩储层性质描述，还可以是不同含油气盆地砂岩储层类型的对比等。代码需要在Excel 2016及以上的版本中运行，否则可能会出现无法编译的情况。操作过程如下：

（1）创建Excel文档，一般情况下，直接创建的文档为不开启宏的状态。点击文件—选项—自定义功能区—在主选项卡中勾选开发工具，Excel 工具栏中出现开发工具选项；再点击信任中心—信任中心设置—宏设置—启用所有宏，点击确定。将文件另存为启用宏的工作簿（即xlsm格式）。

（2）以图10中的表格结构对石英、长石、岩屑数据进行整理，程序中给出了10套地层的自动投点，每一套地层可以容纳4 997 个点，如需增加，可以修改代码。这里需要注意的是，表格的结构框架务必要与图10中完全一致，即从第四行开始是数据，投点列依次为DE、IJ、NO、ST、XY……第十套地层的投点列应为AW与AX。

（3）点击开发工具—Visual Basic—插入—模块—插入—模块，在模块1中粘贴“国内常用”代码，在模块2中粘贴“三边一高”代码，关闭Visual Basic 界面。

（4）点击开发工具—插入按钮（窗体控件）—在Excel表格区域创建两个按钮—分别指定宏指令。

（5）分别点击按钮，即可自动投点生成两类三角图（图10）。本程序给定的诸如框线粗细、坐标轴显示以及各分组中散点的形状与颜色等各种属性的默认值可能不符合作图者的需求，作图者可以在成图后对三角图的这些属性进行修改。

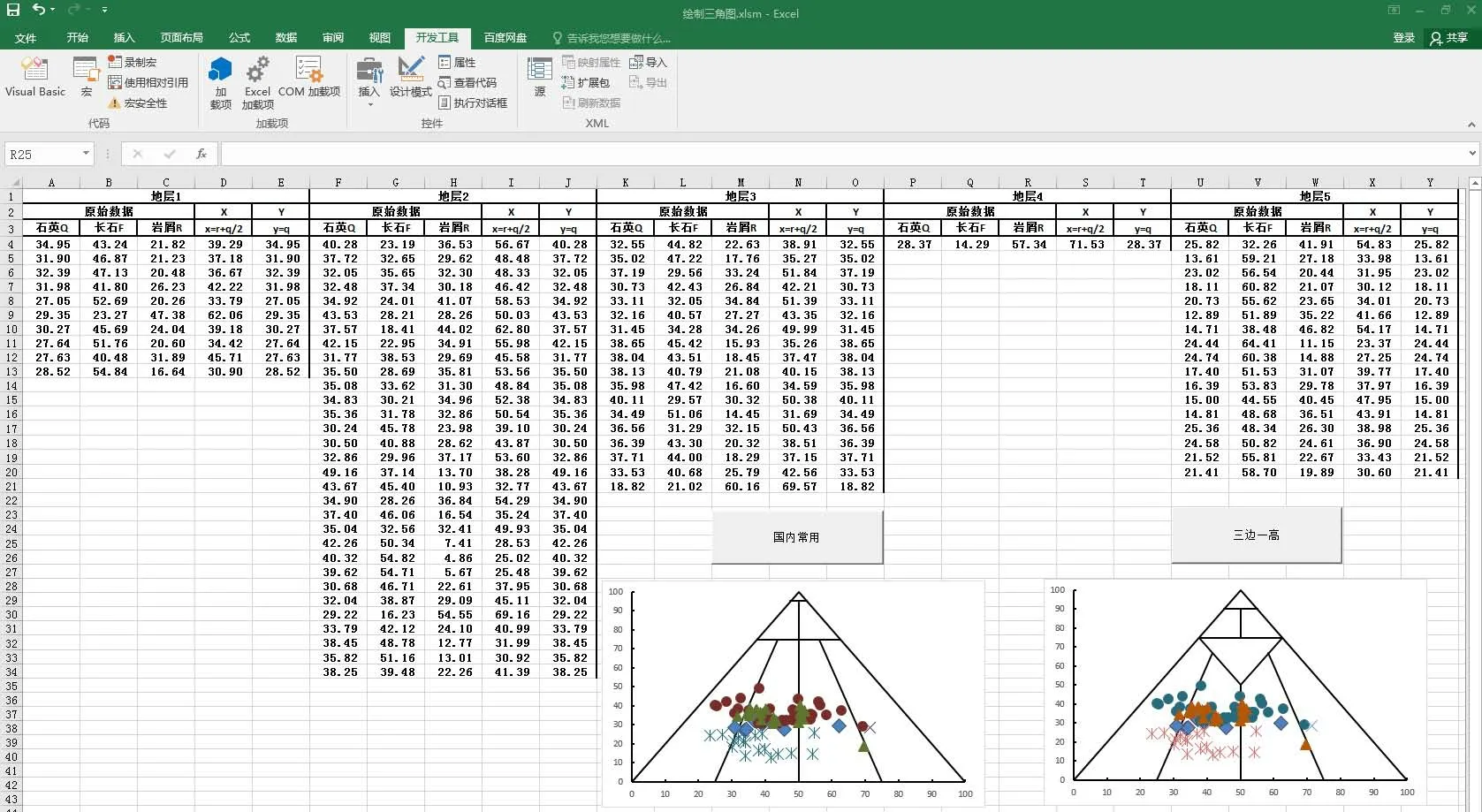
图10 Excel 结构框架与VBA 程序运行效果图Fig.10 Excel structure frame and VBA program running effect chart

7 结论

三角图版对于相加等于1 或100 的三组分的划分十分合理，在地质专业中应用最广泛的当属砂岩分类三角图，种类繁多，各种辅助线纵横交错，但基本的读值投点规则是一致的。如果是三边绝对长度相等的等边三角形，其三条边就可以作为读取数值的坐标轴，经过推导变换，可以将两条侧边作为长石与岩屑的坐标轴，可以将底边上的高作为石英的坐标轴，但“高”的绝对长度并不是石英的含量，某点高值在底边上的高的占比才是石英的含量；如果是底边与高值相等（100）的等腰三角形，其两条侧边则不能作为坐标轴，某点的高值的绝对长度即为石英的含量，通过这一点的平行于X 轴的与三角形相交的内部线段可以作为判断岩屑与长石含量的坐标轴，这条线段上以这一点为分界点，两段长度分别为两种矿物的含量。

前人对于两种三角形的推导的逻辑性错误是由于没有明确分清两种三角图的读值规则区别，投点方式也并非完全一样。此外，按照等边三角形的投点方式拉伸调整成等腰三角形=等腰三角形投点方式的等腰三角形，或者按照等腰三角形的投点方式拉伸调整成等边三角形=等边三角形投点方式的等边三角形这两种容易混淆的转化，使得前人得出“无论是哪种三角形形态，投点规则都是一致的”结论。

Origin 与Grapher 软件可以快速绘制三角图，在没有特别需求的情况下，推荐使用。但涉及到三角形内部的特殊分隔线段、不规则分区、坐标轴标题位置转变以及添加文本描述等情况时，则需要使用Excel 结合地质绘图软件如CorelDraw 等进行绘图。如果需要进行多次绘制三角图版，可以采用本文所附录的VBA程序代码，简化制图过程。

致谢 感谢审稿专家及编辑部工作人员提出的宝贵意见，使论文质量进一步提高。本文所涉及的VBA编程代码可通过国家冰川冻土沙漠科学数据中心获取http://www.ncdc.ac.cn/portal/magazine。