Matlab求解库埃特流在计算流体力学课程中的应用1)

刘 益 付小莉

(同济大学土木工程学院，上海 200092)

课程内容设计应该注重开放性、改变学生的知识观和学习观，并构建以教师为主导、以学生为中心的教学模式[1]。计算流体力学作为机械、航天、车辆乃至土木工程等专业的必修课，兼具有流体力学和工程数学的特点。但对于计算流体力学在内的相关课程，公式多、符号抽象、计算复杂是影响学生学习的绊脚石。另外，由于对以往理论力学等课程的基础概念已经生疏，学生在学习理论基础时常常感到困难[2]。为了摆脱传统教学模式，让学生更好地参与进课程教学中，锻炼学生的编程求解能力，同时拓宽流体力学的教学范围，开展了不可压缩库埃特流的数值解实验，并对不同方法的求解精度与求解效率等方面进行讨论。库埃特流动是一种存在理论解析解的经典流动，非常适合刚刚入门计算流体力学的同学上手实践。

1 问题的提出

库埃特流动是最简单的由剪切力驱动的黏性流动，与复杂的边界层流动具有很多相同的物理特征。其具体问题描述为：设有两个平行的平板，距离为D，上平板以恒定的速度ue运动，下平板则保持静止，试考虑这两个平板之间的黏性流动[3-6]。

1.1 解析解

由纳维−斯托克斯方程进行简化，得到不可压恒温库埃特流动的控制方程

求解该微分方程较为简单，得到解析解如式（2），速度分布为图1所示。

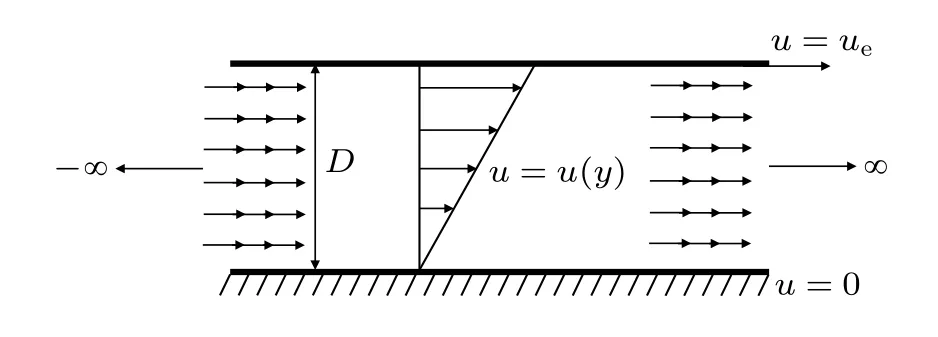
图1 库埃特流动

1.2 数值解

在数值求解时，传统方法采用显式和隐式方法，为了加深学生对数值方法的理解，拟增加第三种迭代算法，即压力修正法进行计算。为了方便后续的讨论，将参数进行无量纲化，定义为

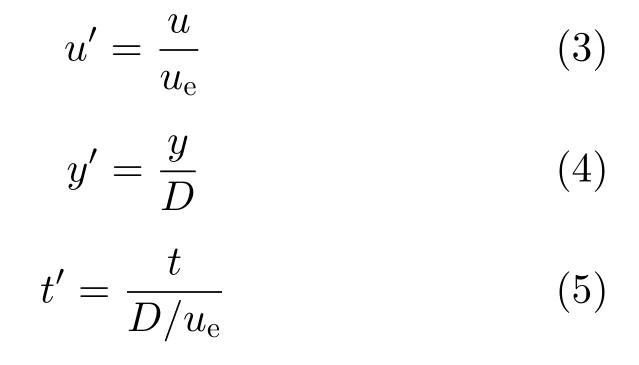
经过化简，得到数值求解的控制方程为

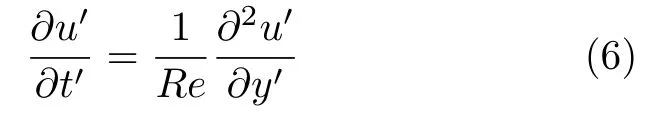
式中，Re为两平板之间距离计算得到的雷诺数。

为了简化记号，本文之后所有讨论的变量上带有的“′”号都将省略。在计算之前，设定初始边界条件为

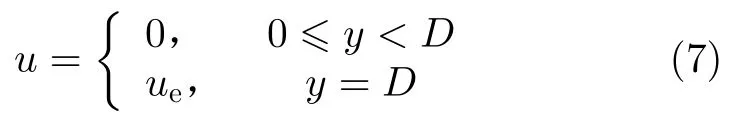
（1）利用显式方法计算时，对时间进行一阶向前差分，对坐标进行二阶中心差分，得到数值求解控制方程为

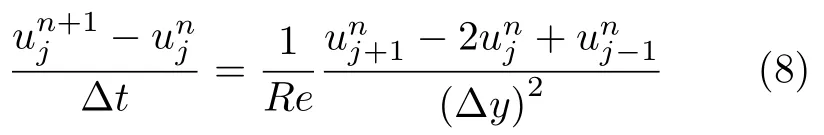
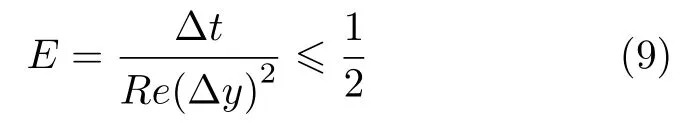
（2）利用隐式方法计算时，采用克兰克−尼克尔森方法求解，该格式无条件稳定，控制方程为

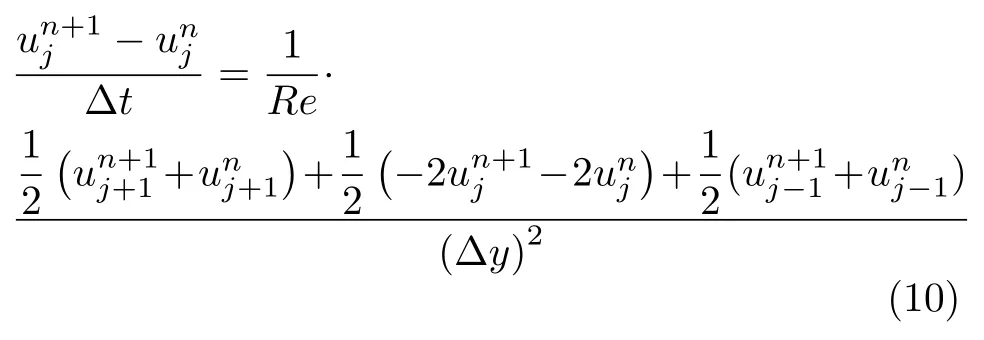
（3）压力修正法的求解基本思路

先假定一个初始条件，在计算区内形成二维流动，然后在迭代过程中观察流场是否收敛到精确解，具体求解流程见图2。

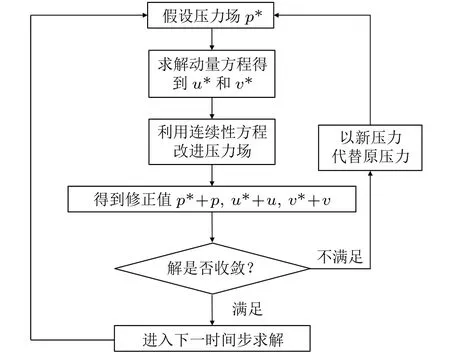
图2 压力修正法求解流程图

2 Matlab求解控制方程

第1节通过差分法得到了显式方法与隐式方法的控制方程，并提出了基于压力修正的第三种方法。本节将采用Matlab编程进行问题求解。

对于显式方法与隐式方法，需要设定边界条件与第一迭代步的初始条件，即为式（7），通过前一迭代步与本迭代步的关系进行求解，显式方法直接将参数代入即可，但是隐式方法需要求解方程组。而压力修正法则与上述二者不同，在给定边界条件时，需要施加一个实际扰动以形成流场，而并非直接进行迭代计算。这里采用两种方式，一种是在中心网格点插入竖直脉冲速度，另一种是在中心网格点插入水平脉冲速度，虽然二者的方向不同，但是在计算收敛性和精确度上是相近的。

图3分别为显式方法、隐式方法、压力修正法（引入竖直脉冲）和压力修正法（引入水平脉冲）的迭代求解收敛图，可以看到，每个关键网格点的速度由一开始设定的初值逐渐向理论解析解靠近。

图3 不同算法收敛图

3 数值计算误差与求解效率分析

计算流体力学乃至整个数值计算的研究领域内，最关心的就是求解精度与效率。为了探究以上问题，本节将集中讨论四个自变量：推进步数、等分数、时间间隔、雷诺数对四种求解方法的误差影响。由于所有网格点中最上方和最下方点的速度已由给定初始条件确定，拟采用中点的速度值作误差对比，其解析解的值为0.5。

3.1 推进步数的影响

控制等分数为10，时间间隔为0.001 s，雷诺数为63.6，而推进步数在50～10 000中变动，其中点速度结果值如表1。

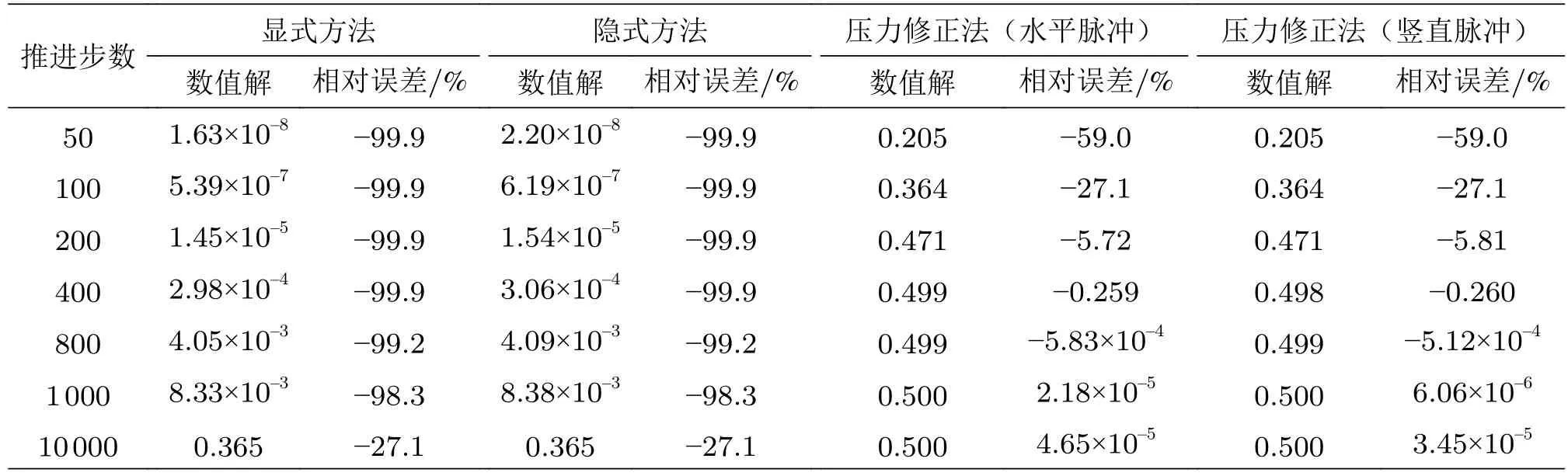
表1 不同推进步数下中点速度值

经过计算可以发现，压力修正法的收敛速度较快，在很少的步数内达到求解收敛，而显式方法与隐式方法求解速度相近，相同情况下需要迭代的步数较多。

3.2 等分数的影响

控制推进步数为10 000，时间间隔为0.001 s，雷诺数为63.6，而等分数在4～16中变动，其中点速度结果值如表2。

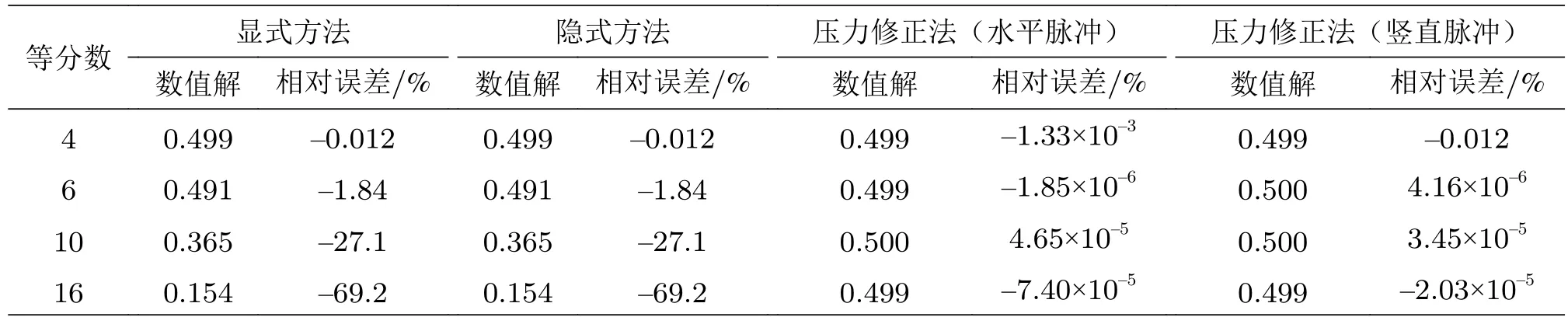
表2 不同等分数下中点速度值

表2表明，随着等分数增大，网格变密，计算速度显著变慢。而压力修正法在不同等分数下仍有很高的精度。尤其在等分数较多时，10 000步内仍然可以达到收敛，也体现其算法的高效。

3.3 时间间隔的影响

控制推进步数为10 000，等分数为10，雷诺数为63.6，而时间间隔在0.001～0.636 s中变动，其中点速度结果值如表3。

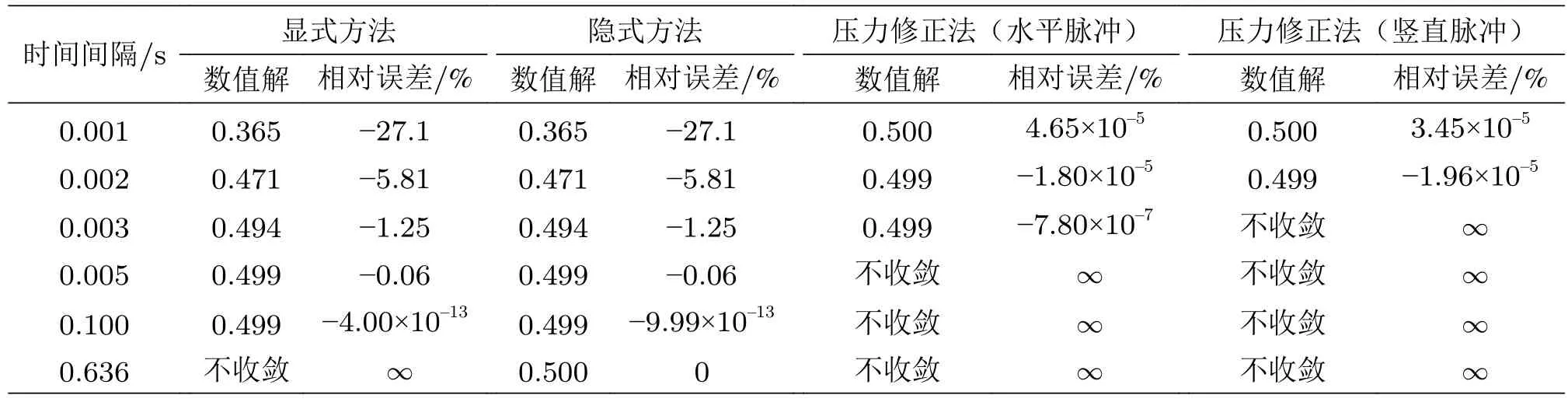
表3 不同时间间隔下中点速度值

计算后，伴随着时间间隔变大，算法开始不收敛，而只有隐式算法是无条件稳定的，但有可能失去时间精度，事实上，存在一个最优的时间间隔使得隐式方法效率最高。而另外三个算法的要求则较高，显式方法一定需要保证稳定参数E≤0.5才能保证收敛，而压力修正法需要在一定限度的时间间隔内才能得到正确答案。

3.4 雷诺数的影响

控制等分数为10，时间间隔为0.001 s，推进步数为10 000，而雷诺数在10～2000中变动，其中点速度结果值如表4。

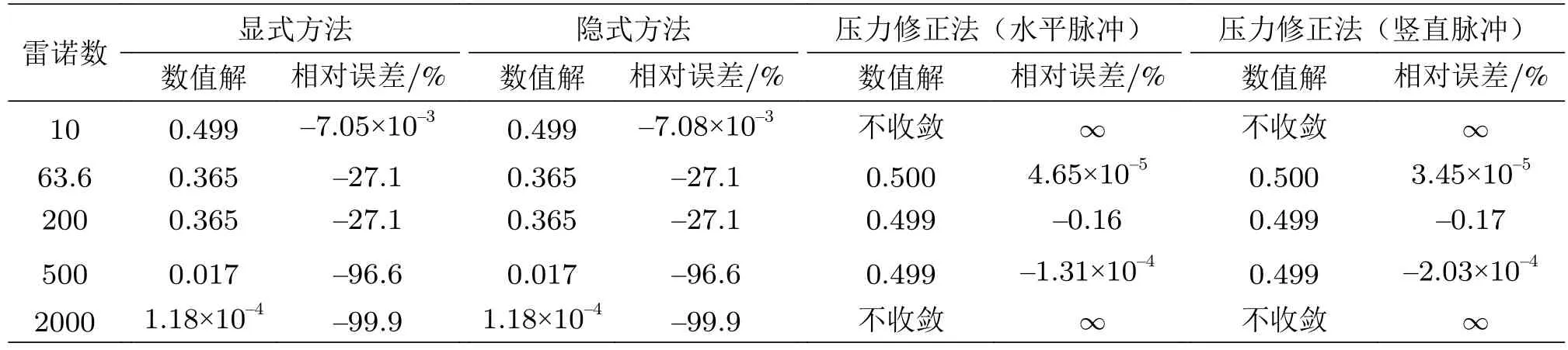
表4 不同雷诺数下中点速度值

从表4可以看出，雷诺数对压力修正法影响较大，由于压力修正法是经过连续性方程和动量方程耦合联立推导得到的，在数值解的情况下更具有实际意义，即需保证存在真实的流场满足参数设定，否则有可能在极端条件下不收敛。另一方面，雷诺数变大也会影响显式与隐式方法的收敛速度，但是对于收敛性的影响不大，隐式方法在不同雷诺数情况下均能收敛。

从以上四个变量的计算中得到结论，显式算法与隐式算法对时间间隔的大小与等分数比较敏感，即编程者需要确定一个合适的网格划分尺寸与计算精度；而压力修正法对雷诺数等较为敏感，在雷诺数较高或不符合实际的情况下，有可能导致数值振荡，影响求解的精度与效率。

4 结语

大学教师往往更重视对学生专门知识与多项技能的培养[7]，而大学课堂上的教学除了最基本的教授知识外，更重要的是教给学生获取知识的方法和激发学生的学习兴趣，由此才能让学生主动去学习对自己有帮助的课程与知识[8]。本文通过一个非常经典的流动模型，来启发学生通过多种方式进行数值求解，并探究基本参数与误差之间的影响关系。经过练习，学生能很好地入门计算流体力学领域，了解求解的一般方式与步骤，锻炼编程能力和作图能力，为后续的学习科研打下基础。