梯度蜂窝加筋板的弯曲变形及优化设计1)

2022-08-19张晨帆邓庆田李新波宋学力

力学与实践 2022年4期

张晨帆邓庆田李新波宋学力

(长安大学理学院，西安 710064)

多孔结构设计方法与成形性能的研究[1-4]主要集中于均质多孔结构，而均质多孔结构往往无法满足实际应用中复杂非均质的应力应变状态的需求，且均质多孔结构并非是最优化的结构分布状态。因此可以通过模仿自然界中多梯度多孔结构的分布模式，根据结构的局部特性合理地分布多孔材料，深入研究梯度多孔结构的力学性能和失效行为，从而对结构加以优化。

梯度多孔结构[5-11]在骨骼、树干和竹子等生物结构中为常见的一种生物梯度微结构，具有优秀的吸能、减震和抗弯等力学性能，被广泛应用于航空航天、建筑工业、生物医疗等领域。有关梯度蜂窝结构的研究已有很多，卫禹辰等[12]通过改变内凹蜂窝型梯度结构胞元尺寸与胞元凹角，分析了梯度结构在爆炸冲击环境下冲击波衰减效率和力学响应规律。Shao等[13]研究了不同压缩速率对梯度木制素蜂窝变形行为和压碎应力的影响。

本文基于三点弯曲实验的加载位置及支承方式，将梯度蜂窝型胞元引入加筋板加筋层设计当中，通过控制质量参数，分别设计制备壁厚梯度形式和孔隙率梯度形式两种梯度多孔结构加筋板，研究梯度多孔蜂窝结构对加筋板弯曲性能的影响。

1 模型设计及参数

1.1 设计思路

由文献[14]可知三点弯曲实验下蜂窝加筋板的破坏模式总是在承载位置处的加筋肋壁上开裂失效，因此试件中心位置是主要受力位置，容易因应力集中现象而破坏。在加筋板结构中，多胞壁蜂窝较单胞壁蜂窝具有可设计性、承弯能力强等优势，因此将多胞壁蜂窝引入加筋层设计中。本文基于三点弯曲实验的加载方式，在蜂窝胞元均匀排列的加筋板加筋层上，合理改变壁厚和孔隙率使其由承载处到两侧呈梯度形式排列，同时控制试件质量为常量，通过在压头位置处增大壁厚和减小孔隙率来增强加筋板的承载能力。

1.2 梯度形式设计

以内凹形蜂窝胞元的试件为例，如图1所示。加筋板长为L，宽为b，加筋层胞元布局均左右对称，取一半进行分析并将其等分为3个区域。梯度形式的设计是严格遵循结构等质量原则，壁厚梯度形式设计时孔隙率不变，试件A-0-t蓝色区域的壁厚与试件A-0一致，由于加筋层等厚度，因此需控制试件A-0-t红色与黑色区域的胞壁面积之和等于蓝色区域胞壁面积的两倍。令胞元面积为A，三个区域胞元数目分别为n1,n2,n3，则壁厚梯度形式的控制函数为

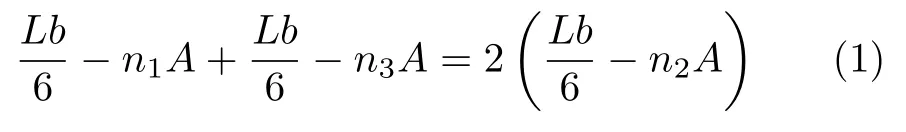
图1 内凹构型三种胞元布局形式下的平面图Fig.1 Plan view of three cell layout forms of reentrant configuration

化简可得

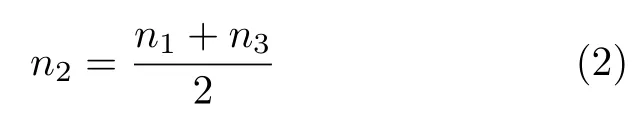
同理，在孔隙率梯度形式的设计中，需使试件A-0-n红色与黑色区域的胞壁面积之和等于蓝色区域的两倍，三种孔隙率下的胞元面积分别为A1,A2,A3，三个区域胞元数目分别为n1,n2,n3，则孔隙率梯度形式的控制函数为

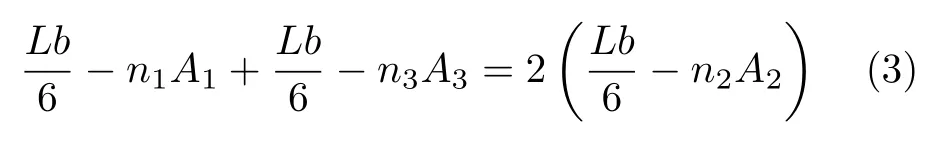
化简可得

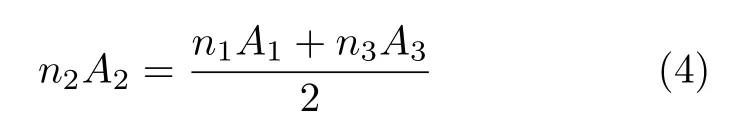
因此通过控制胞元数目来确定孔隙率，从而保证同类型的结构总质量一致。对正六边形胞元梯度形式的设计思路也是如此。设计出的各种试件的加筋层平面如表1所示。

表1 各种试件的加筋层平面Table 1 Plane of stiffened layer of various specimens

1.3 模型参数

加筋板由蒙皮层与加筋层组成，如图2所示。蒙皮层为实心板，加筋层为蜂窝胞元，蒙皮层与加筋层厚度分别为h1和h2，本文中所设计的加筋板L= 120 mm，b= 70 mm，h1=h2=4 mm。

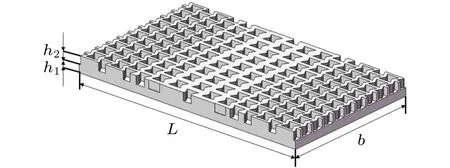
图2 加筋板示意图Fig.2 Schematic diagram of stiffened plate

图3为加筋层单个蜂窝胞元的几何参数示意图，其中，a表示孔隙边长，h为孔高，θ表示孔隙夹角，t表示壁厚，n表示孔隙率。本文中所设计的不同孔隙率下蜂窝胞元几何尺寸如表2所示，各结构的壁厚与孔隙率如表3所示。为便于描述，用A代表内凹形蜂窝胞元，B表示正六边形蜂窝胞元，0和90分别表示水平方向与竖直方向，例如A-90-t就表示为内凹形蜂窝胞元竖直方向且壁厚呈梯度形式分布，而 A-90则表示内凹形蜂窝胞元竖直方向均匀分布。

表3 不同分布形式下的壁厚及孔隙率Table 3 Wall thickness and porosity under different distribution forms

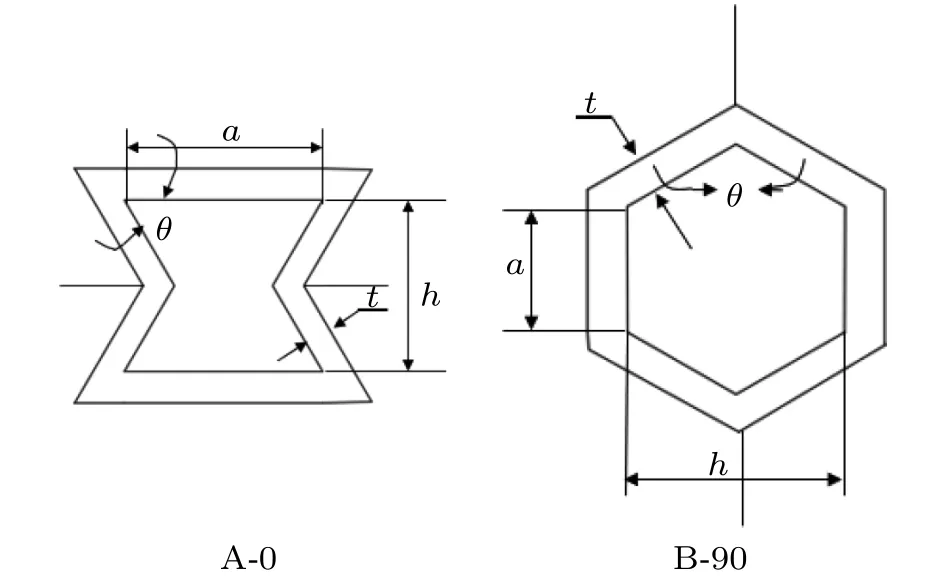
图3 单个蜂窝胞元几何参数示意图Fig.3 Schematic diagram of geometric parameters of a single honeycomb cell

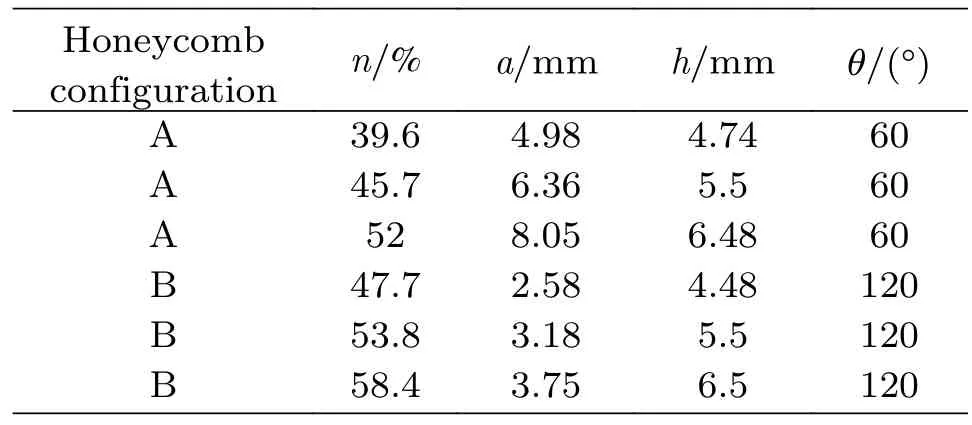
表2 蜂窝胞元几何参数Table 2 Geometric parameters of honeycomb cells

2 研究方法

2.1 材料参数

用3D打印机制备实验试件，基材选用聚乳酸(polylactic acid, PLA)，其材料参数依据单轴压缩实验（GBT 1041−1992）测试得到[15]。首先制备出标准压缩试件，试件几何尺寸如图4(a)所示，使用万能试验机对标准试件进行准静态压缩实验，加载速率为1 mm/min，压缩应变至0.14，测得材料应力–应变曲线如图4(b)所示。由本构曲线测得基材弹性模量E= 2 200 MPa，屈服应力σ =45.7 MPa，泊松比μ= 0.35。

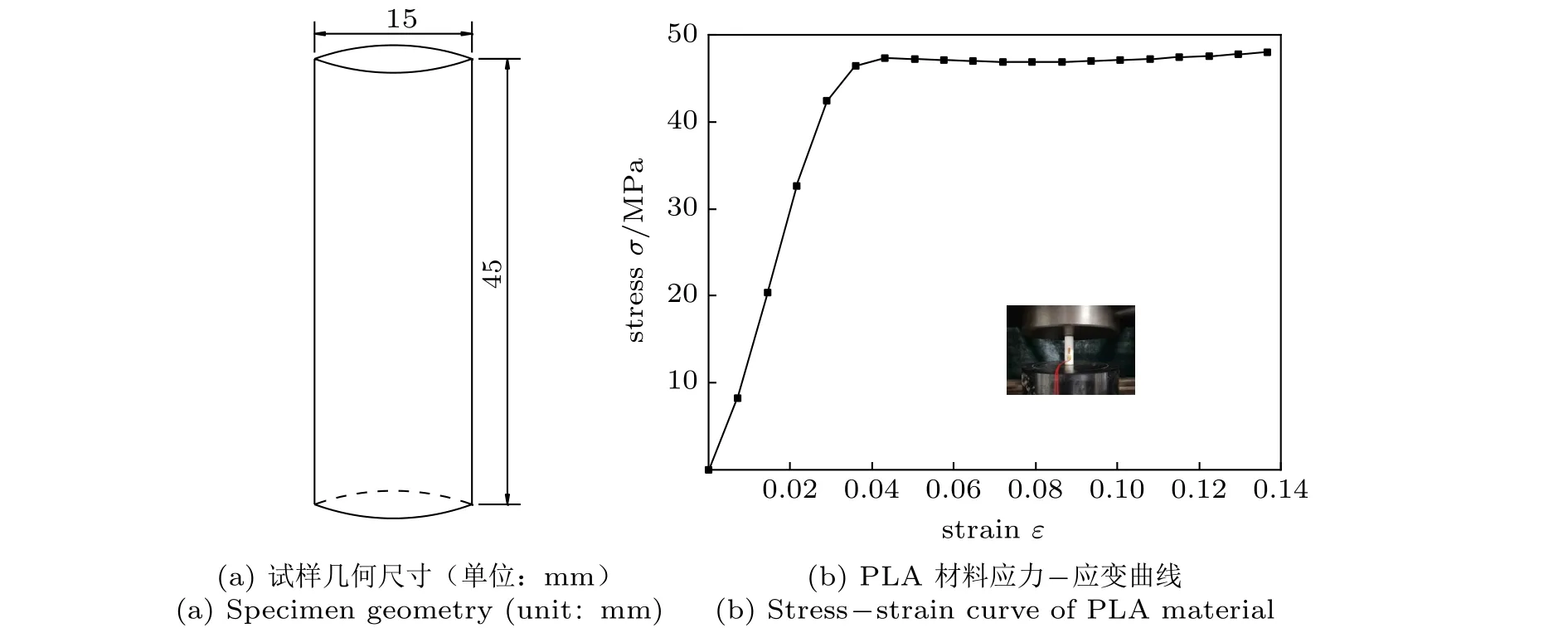
图4 试样尺寸及基材本构曲线Fig.4 Specimen size and substrate constitutive curve

2.2 有限元模型

采用ANSYS Workbench/Static structural模块模拟加筋板准静态三点弯曲实验，按照所测材料PLA本构参数进行自定义，压头及两支座与实验试件之间为摩擦接触，摩擦系数为0.15，采用四面体SOLID 187单元对结构进行网格划分，网格单元尺寸为3 mm，两支座底面施加固定约束，在压头处分步施加位移载荷至40 mm，载荷步分5步，后处理分析加筋板的弯曲变形模式以及应力分布情况。有限元模型如图5所示。

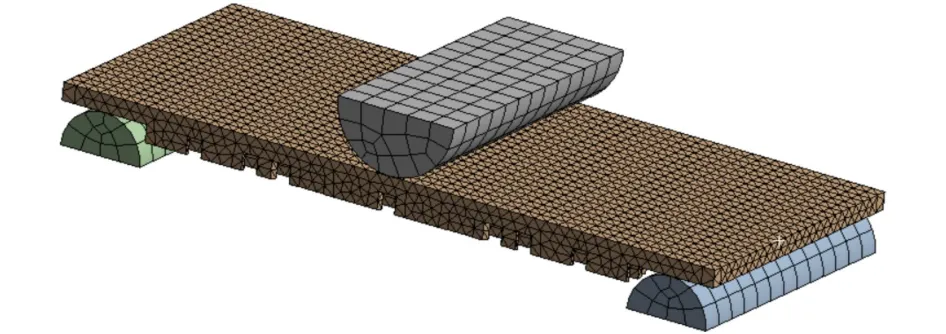
图5 加筋板有限元模型Fig.5 Finite element model of stiffened plate

2.3 实验测试

实验在室温条件下进行，使用万能试验机（图6(a)）逐一对试件进行准静态加载，支座跨距为140 mm，试验入口力为15 N，以1 mm/min的速率匀速加载至40 mm后结束返车，采用位移传感器连接电脑采集装置实时记录并保存实验数据，同时用摄像机记录试件压缩方向的变形过程。实验加载装置如图6(b)所示。实验试件采用增材制造熔融沉积成型工艺制备，图6(c)为制备出来的试件。

图6 实验设备及试件制备Fig.6 Experimental equipment and specimen preparation

2.4 验证有限元模型

通过对每个试件进行仿真分析与实验测试，几种试件在压缩方向上变形过程如图7所示，可以看出各试件弯曲变形形貌有限元结果与实验结果吻合较好，值得注意的是，蜂窝胞元壁厚呈梯度形式排列（试件A-0-t与B-0-t）的实验结果并不在承载位置处破坏失效，这是因为这两种试件最中心位置处加筋层壁厚最大，抵抗开裂的能力较强，所以在同等压缩位移载荷下，试件从加筋层中心位置附近壁厚相对较小的位置率先开裂失效。图8给出了其中两个试件压缩载荷位移曲线与不同阶段加筋层变形形貌的有限元结果与实验结果，引起较大误差的原因是有限元结果没有模拟出试件加筋层的开裂现象，而实验测试时，试件加筋层由于承受极限压应力会在肋壁处发生断裂破坏。但两种结果在小变形阶段基本吻合，且实验结果中加筋层开裂的位置与有限元应力云图中峰值应力的位置相对应，这两点均可验证有限元模型的可靠性。为了准确描述实际结果，后面基于实验结果进行分析与讨论。

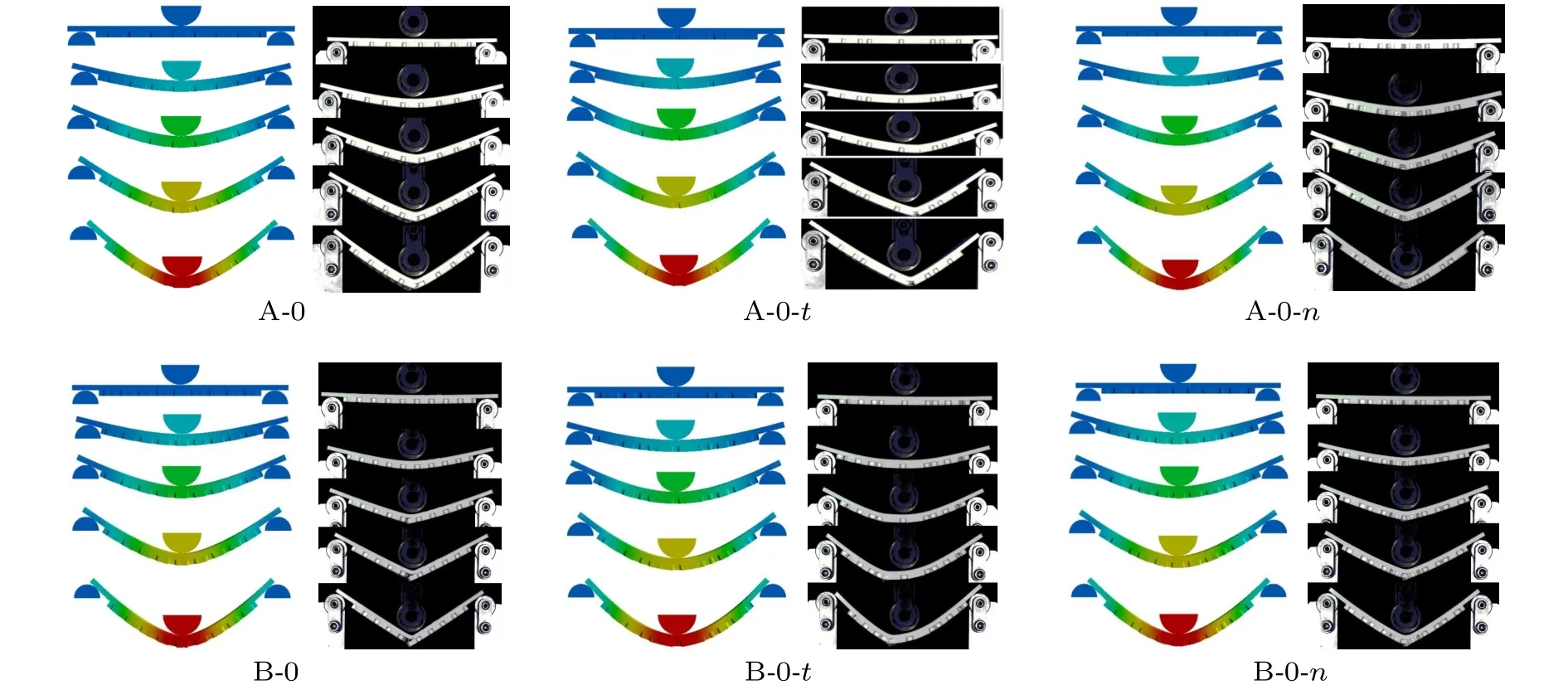
图7 压缩变形过程有限元与实验结果Fig.7 Finite element and experimental results of compression deformation process

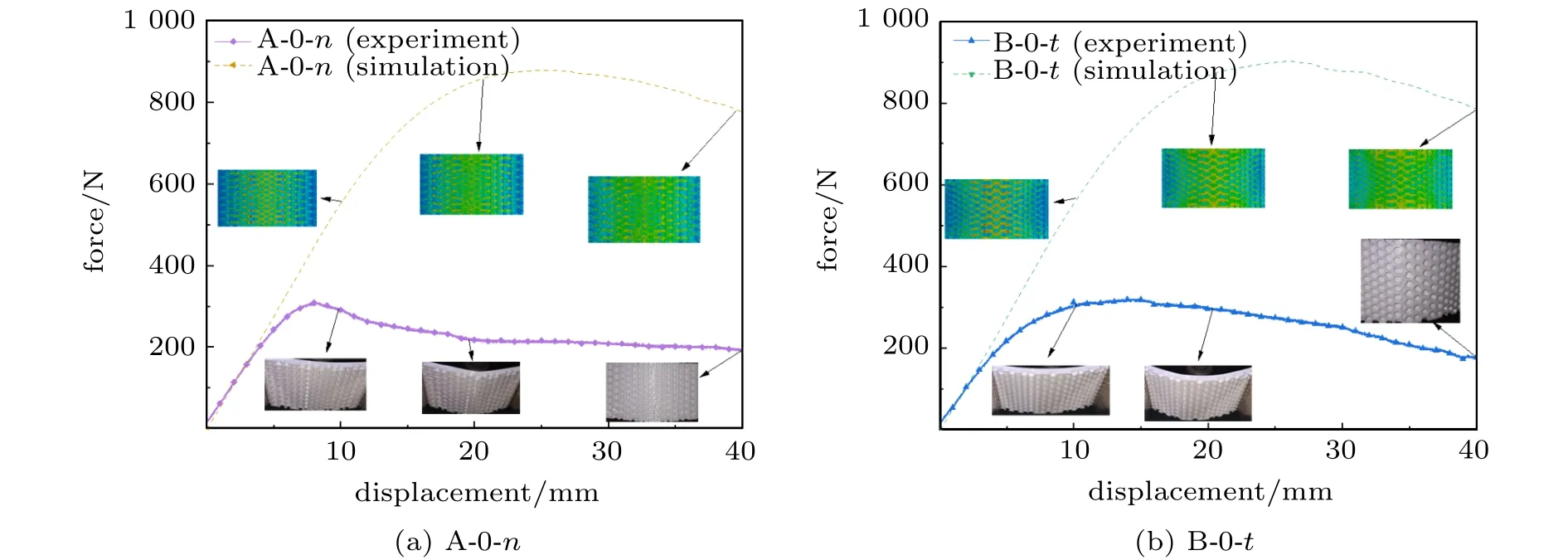
图8 载荷位移曲线及加筋层变形形貌的有限元与实验结果Fig.8 The load-displacement curve and the finite element and experimental results of the deformation morphology of the reinforcement layer

3 结果与讨论

3.1 梯度形式对加筋板弯曲变形的影响规律

图9给出在不同排列形式下各类试件的载荷位移曲线，在等质量条件下，加筋层为内凹六边形蜂窝胞元且水平方向排列时，壁厚梯度形式下结构承载性能最强，峰值承载力较孔隙率呈梯度形式分布提升了21%，且后者最先开裂破坏。竖直方向时，孔隙率梯度形式下结构承载性能最强，峰值承载力较壁厚梯度形式分布提升了14%；加筋层为正六边形蜂窝胞元且水平方向排列时，均匀形式下在弹性阶段达到峰值载荷后，加筋层迅速开裂导致承载力迅速下降，而壁厚梯度形式下加筋层缓慢开裂，开裂完全后载荷缓慢下降，孔隙率梯度形式下结构承载力最低，加筋层开裂后载荷保持不变，竖直方向时，加筋层在三种排列形式下结构承载力相差不大，但开裂时刻位移表现出不同规律，其中壁厚梯度形式最先开裂，均匀分布次之，而孔隙率梯度形式最后开裂。综合上述结果可知，试件A-0-t，A-90-n在同类别中均对结构承载力表现出正效应，而梯度形式对正六边形蜂窝胞元结构的正效应并不显著。表4给出各试件的峰值承载力与初始断裂时刻位移，可以看出，所有试件均在压缩位移20 mm之前出现断裂，孔隙率梯度形式且竖直方向分布时结构出现断裂时刻相对较晚，表明这种形式下结构韧性较强。

表4 各试件的峰值承载力与初始断裂时刻位移Table 4 Peak bearing capacity and initial fracture displacement of each specimen

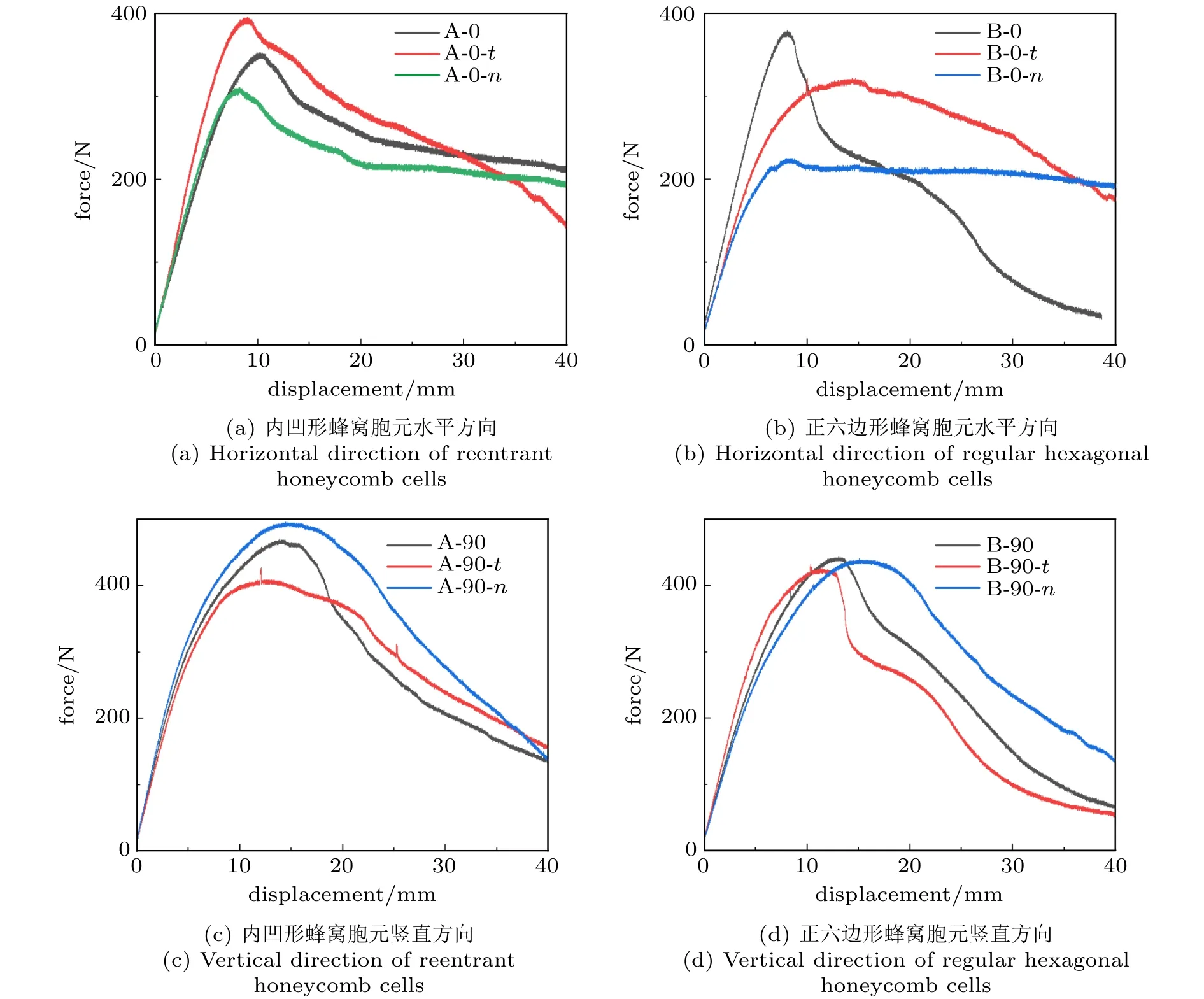
图9 不同分布形式下各种试件的载荷-位移曲线Fig.9 Load–displacement curves of various specimens under different arrangements

3.2 胞元方向对加筋板弯曲变形的影响规律

由上述结果可知，蜂窝胞元的分布方向对结构弯曲变形也有一定影响。图10给出了各试件不同胞元方向下的载荷–位移曲线，可以看出，不论是内凹六边形蜂窝还是正六边形蜂窝，当胞元竖直方向排列时结构承载性能较水平方向有明显提升。结合表4可得，试件A-90峰值力较试件A-0提升了25%，试件A-90-t峰值力较试件A-0-t提升了8%，试件A-90-n峰值力较试件A-0-n提升了37%；试件B-90峰值力较试件B-0提升了14%，试件B-90-t峰值力较试件B-0-t提升了26%，试件B-90-n峰值力较试件B-0-n提升了49%。

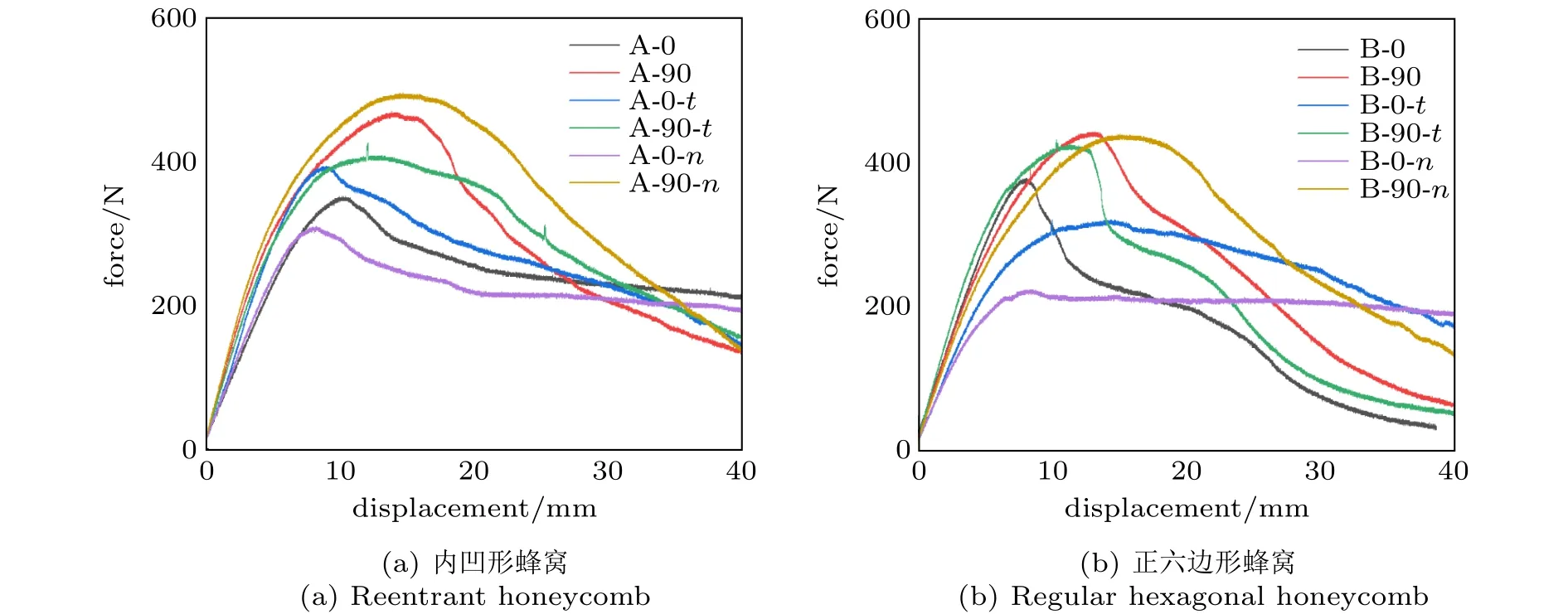
图10 不同胞元方向下各类试件载荷–位移曲线Fig.10 Load-displacement curves of various specimens in different cell directions

3.3 加筋层优化分析

复合材料板的质量优化设计可以减少纤维用量，降低成本[16]。基于加筋板实验结果的破坏模式可知加筋板的主要承载位置是与压头接触的中心位置，加筋层两侧并没有开裂且应力较小。因此，为提升材料利用率，基于有限元分析中的应力分布图进行的曲线拟合设计，将加筋层优化为曲面形式，如图11所示，加筋层中心位置处厚度保持不变，加筋板长和宽两个方向的厚度均由中心向两侧呈曲线形式递减至0。对经优化后的试件进行了相同实验，得到载荷–位移曲线如图12所示。

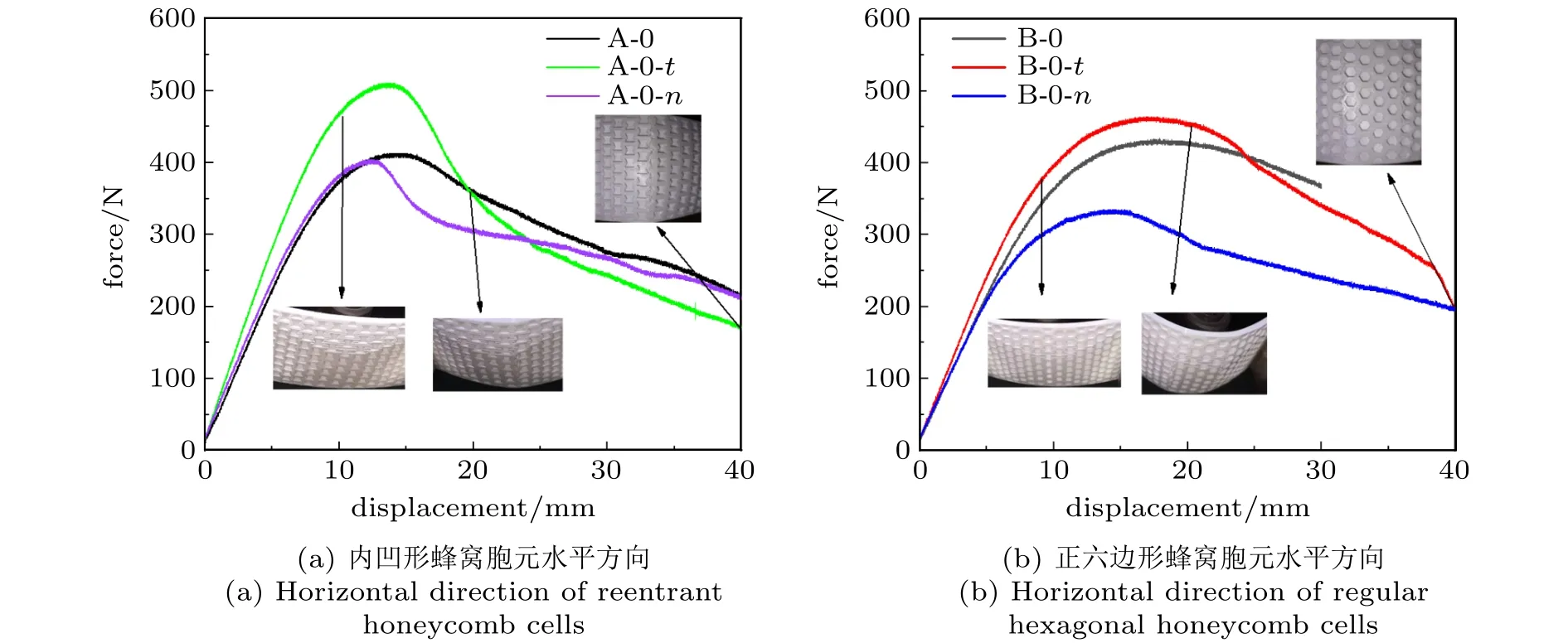
图12 加筋层为曲面形式的载荷–位移曲线Fig.12 Load–displacement curve of the reinforced layer in the form of a curved surface

从图11可以看出，将加筋层优化为曲面后依然体现出蜂窝胞元梯度形式在提升加筋板承载性能方面的优越性。从提升材料的利用率出发，由于优化后的试件质量变小，因此将比吸能[17-18]作为指标进行判断。吸能量EA代表准静态压缩过程中，结构在一定压缩位移下的吸能量，其数学表达式为

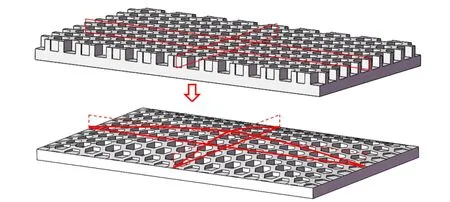
图11 加筋层优化示意图Fig.11 Schematic diagram of reinforcement layer optimization

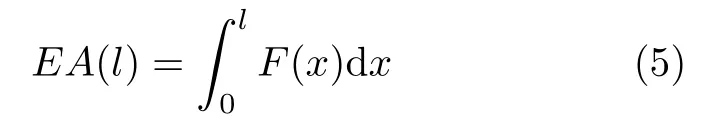
式中，l为压缩位移，F(x) 为瞬时承载力。比吸能SEA为结构单位质量的吸能量，其数学表达式为

式中M为结构总质量。由于加筋层形式不同，各种类型的试件总质量存在差异。其中，内凹六边形蜂窝胞元在平面形式下结构总质量为0.081 kg，在曲面形式下结构总质量为0.062 kg；正六边形蜂窝胞元在平面形式下结构总质量为0.077 kg，在曲面形式下结构总质量为0.06 kg，由式（6）计算可得各种试件在两种加筋层形式下的吸能量与比吸能如表5所示。

表5 各种试件的吸能量与比吸能Table 5 Energy absorption and specific energy absorption of various specimens

从表5可知，加筋层为曲面形式时结构比吸能显著高于平面形式，这表明将加筋层改进为曲面形式后，能显著提升材料的利用率，使结构在质量较小的条件下达到较好的吸能特性，从而减少经济损耗。此外，加筋层壁厚梯度形式下结构的吸能量相对其他两种形式更高，而孔隙率梯度形式下由于蜂窝胞元以及胞元方向的不同而表现出不一致现象，加筋层为正六边形蜂窝胞元时，不论哪种胞元方向，孔隙率梯度形式下结构吸能量高于均匀分布；加筋层为内凹六边形蜂窝胞元且竖直方向分布时，孔隙率梯度形式下的吸能量同样高于均匀分布，而当蜂窝胞元水平方向分布时，孔隙率梯度形式下的吸能量则低于均匀分布。

3.4 压头位置对加筋板弯曲变形的影响规律

通过对实验结果分析可知三点弯曲实验压头位置的偏差对结果有很大影响。为了研究压头位置对加筋板弯曲变形的影响规律，将压头轴线与水平方向之间的夹角记为θ，如图13所示，依次取 θ为 30°，45°，60°，90°。对试件 A-0，B-0，A-0-t，A-0-n进行实验测试，图14为θ取不同值时各试件的载荷–位移曲线，几种试件的结果均表明加筋板承载力随θ角增大而减小，即压头越倾斜，加筋板的承载能力越强。实验过程伴随着加筋层丝裂的声音，θ取30°时试件A-0由于变形过大在压缩位移27 mm时刻就完全破坏。图15为压缩方向的弯曲变形过程，相较于实验过程的变形形貌，有限元结果较为理想，而实验结果表现出的加筋层破坏模式更具实际意义。图16为不同压头位置下试件A-0的有限元应力云图，可见加筋板的峰值应力随θ角增大而减小，θ为30°时峰值应力较90°提升了64%。

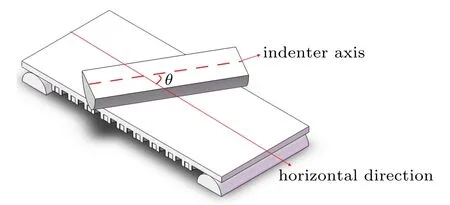
图13 压头位置示意图Fig.13 Schematic diagram of the position of the indenter

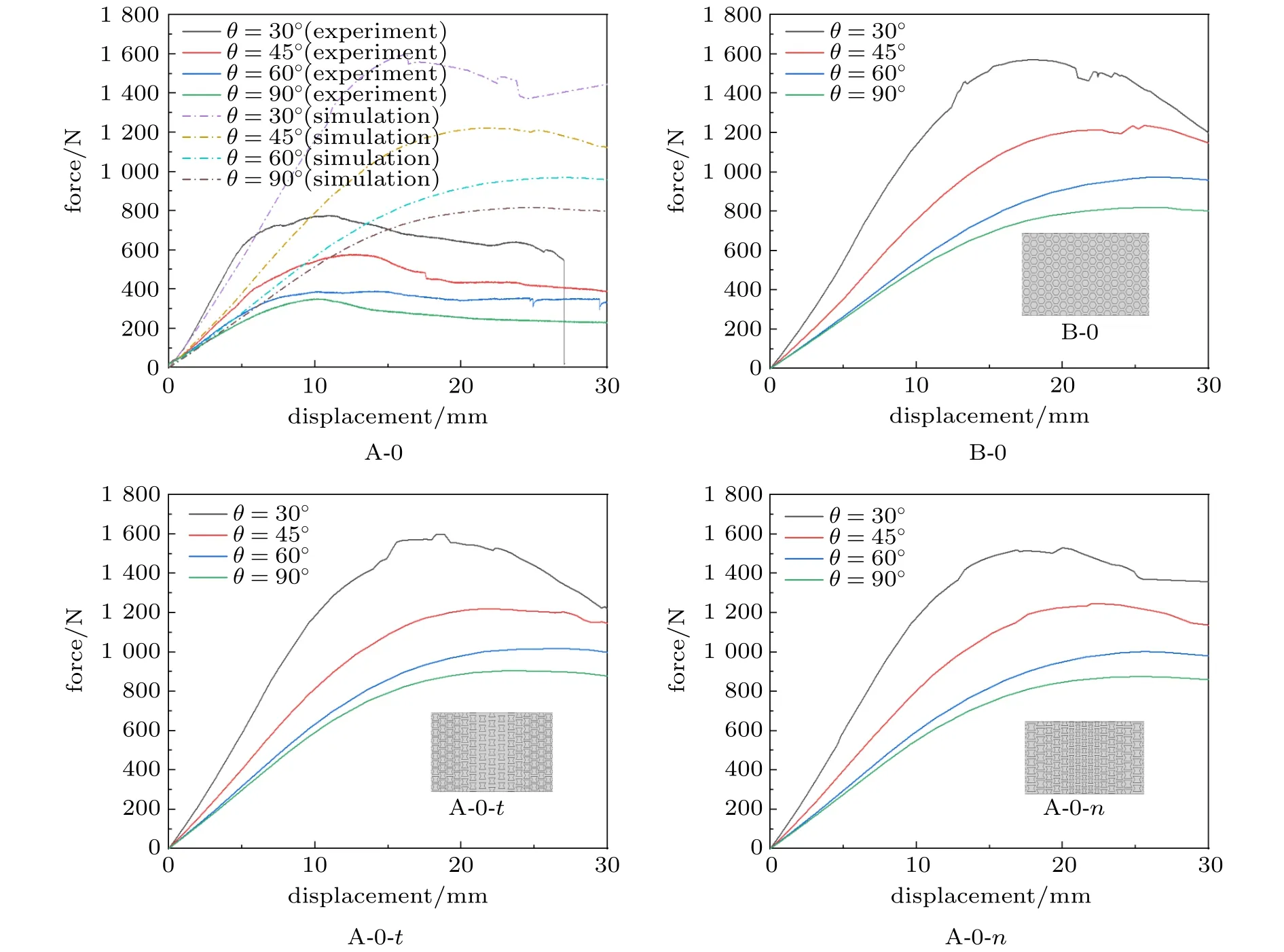
图14 不同压头位置下各试件的载荷–位移曲线Fig.14 Load–displacement curve of each specimen under different indenter positions

图15 不同压头位置下试件A-0的弯曲变形过程Fig.15 Bending deformation process of specimen A-0 under different indenter positions

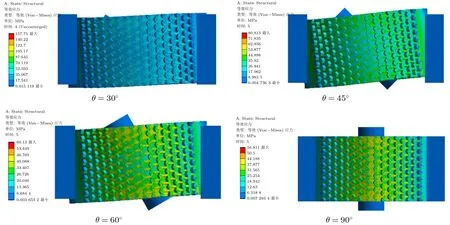
图16 不同压头位置下试件A-0的有限元应力云图Fig.16 Finite element stress cloud diagram of specimen A-0 under different indenter positions

3.5 加筋层开裂位置分析

由于在压缩方向上摄像机并未捕捉到加筋层蜂窝胞元的变形形貌，结合实验结果可知压头位置对加筋层破坏形式有一定影响。图17给出了不同压头位置下加筋层的破坏模式，由图可知，在不改变压头位置，即压头轴线垂直于水平方向（θ = 90°）时，加筋层是从蜂窝胞元肋壁处开始开裂破坏，而将压头位置改变不同角度后，加筋层是从与蒙皮层交界处开始脱裂破坏。