融合节点重要性的无监督链路预测算法

傅馨玉，顾益军

中国人民公安大学 信息网络安全学院，北京 102600

链路预测是研究复杂网络[1]的核心内容之一，在生物研究[2]、电子商务[3]、合作推荐[4]、社会安全[5]等众多领域得到广泛的实际应用。在复杂网络中，将个体称为节点，节点间的关系称为连接。链路预测，即根据网络中的已知节点以及节点间的连接情况等信息，预测该网络中任意两个未连接节点之间可能会产生新连接的概率[6]。近年来，随着机器学习、深度学习的不断发展，一些有监督式链路预测方法[7]成为研究热点，通过定义损失函数训练模型或者利用先验知识来进行链路预测，学习训练的过程通常需要大量的时间成本。现实世界中网络数据集多为“小世界”[8]模型下的加权复杂网络，对于一些小规模、需要快速预测的网络，往往不需要采用有监督式链路预测方法，消耗大量的训练时间，并且小规模数据集下训练的效果较差。反而一些无监督式链路预测方法，在保证预测精确度的同时，可以高效快速输出预测结果，更适用于解决此类加权网络链路预测问题。无监督式链路预测方法可以分为基于似然分析的预测方法[9]和基于相似性[10]的预测方法。基于似然分析的预测方法需要不断更新样本，时间复杂度较高，不具备普遍适用性。常用的基于相似性的预测方法，计算信息容易获取，算法复杂度低，并根据网络结构信息量的多少，可以划分为基于局部网络结构和基于全局网络结构的预测指标。在真实加权网络数据集中，存储、计算权重信息和路径信息会增加算法的时间复杂度，因此在一些小规模、需要及时解决的事件预测问题上，基于局部网络结构的无监督预测方法更为适用。

然而，这类方法通常仅考虑节点度[11]、共同邻居[12]、边权值[13]、路径[14]等信息，忽略了节点自身重要性对新连接产生的影响。“中心性”常用来刻画网络中节点的重要程度，应用到无权网络的相关研究上[15-16]。在真实加权网络上，受到亲近关系、传播阻塞等现实因素影响，会出现低中心性节点同样具有高重要性的情况，对链路预测结果产生一定影响。

针对上述问题，将无权网络上节点重要性的研究更多地延展到加权网络上，分析节点重要性影响连接产生的方式以及不同中心性下的影响差异，并应用到加权网络链路预测方法中。本文的主要贡献包括：（1）证明了在现实加权网络中，中心性小的节点反而越重要，产生新连接的可能性越大，节点重要性在链路预测问题研究中起到重要作用；（2）提出一种融合节点重要性的无监督链路预测算法FNI（unsupervised link prediction algorithm fusing node importance），相比同类基于局部网络结构的无监督预测方法提高了精确度；（3）对比图嵌入等有监督式链路预测方法，无监督的FNI算法能够更加准确地解决现实里小规模加权数据集上的快速预测问题。

1 加权网络链路预测相关研究

当前加权网络链路预测相关研究方法相比无权网络较少，可以分为有监督式和无监督式链路预测方法。

1.1 有监督式链路预测方法

机器学习、深度学习领域不断提出各种有监督式方法用于解决链路预测问题，最为常用的就是图嵌入方法，主要包括基于矩阵分解、随机游走和深度学习的图嵌入方法。Ou 等人[17]针对有向图中的非对称传递性，将嵌入分为源嵌入和目标嵌入，提出基于矩阵分解的HOPE（high-order proximity preserved embedding）算法；Grover等人[18]通过调整深度优先搜索和广度优先搜索策略的参数，用Skip-Gram模型对生成的游走序列进行嵌入，提出基于随机游走的Node2vec 方法；Wang 等人[19]提出基于深度学习的SDNE（structural deep network embedding）方法，保持一阶和二阶相似性，利用高度的非线性函数和优化目标函数生成嵌入向量。这些方法通过大量的迭代轮数，最小化各自定义的损失函数，得到最佳的嵌入向量表示，计算节点向量间的相似性输出预测结果。然而，监督训练过程往往需要大量的时间，且存在训练结果较差的可能，在小规模加权网络上并不具备训练的必要性，时间成本投入和预测结果收益不成正比。

1.2 无监督式链路预测方法

基于似然分析的预测方法通常适用于规模庞大的网络，在加权网络上边的存在性可以用泊松的似然程度来表示。具有代表性的是泊松随机分块模型、度修正的泊松随机分块模型以及非负矩阵因子分解模型。这类算法的时间复杂度较高，且不适用于小规模网络的连边预测。

基于局部网络结构的预测方法主要可以分为基于局部信息、路径信息以及局部与路径相结合的三类指标。在基于局部信息的预测指标中，Lv等人[20]将经典相似性指标拓展到加权网络上，提出了WCN（weighted common neighbors）、WAA（weighted Adamic-Adar）、WRA（weighted resource allocation）三种经典指标。在共同邻居的基础上考虑两端节点度的影响，WCN 指标从不同角度衍生出WSalton、WSØrensen、WHPI（weighted hub promoted index）、WHDI（weighted hub depressed index）、WLHN-I 五种加权指标。这一类指标很好地结合了节点强度和权重值，计算复杂度低，但计算方式仅限于存在共同邻居的两阶路径下，高阶相似性并没有得到充分计算。

基于路径的预测指标可以写成统一的形式：

其中，Sxy表示节点相似性，α表示可调参数，A为含权邻接矩阵。区别在于路径的步长限制不同，最为常用的是加权局部路径指标WLP（weighted local path），其将路径步长限制在三步之内。这一类指标从路径的角度出发，全面考虑多路径、高阶路径对节点相似性的贡献，反而忽略了节点自身属性在链路预测问题中的重要作用。

综合上述两类指标各自的优缺点，学者们不断提出局部与路径信息相结合的指标。Zhao 等人[21]通过路径权重的乘积衡量该路径对节点间相似性的贡献程度，定义可信路径加权指标rWCN（reliable-route WCN）、rWAA（reliable-route WAA）和rWRA（reliable-route WRA）。Bai等人[22]提出了节点与路径相结合的半局部预测指标WRALP（weighted resource allocation along local path）。刘苗苗等人[23]定义边权强度、路径相似性贡献，并限制路径长度来计算相似性得分，提出了基于多路径节点相似性的预测指标STNMP（similarity based on transmission nodes of multi-path）。白杨等人[24]提出了将可靠路径与WRALP相结合的预测指标PWRALP（product-WRALP）。虽然这一类预测指标，相比前两类指标具有更高的预测精确度，但仅凭相似程度来判断节点间建立新连接的可能性，忽略了节点重要性作为节点的重要属性之一，同样会影响新连接产生的可能性。

2 FNI算法

2.1 节点重要性对连接产生的影响

真实网络中，新连接的产生具有一定的随机性，并非任意产生。链路预测是在遵循概率分布的基础上，区分不同连接产生的可能性，从而给出预测结果。节点重要性则会在一定程度上影响到这种可能性，原因在于一些亲密关系强、传播信息快的重要节点，往往更容易与其他节点建立通话接触、信息传递、合作互利等不同现实意义上的关系，增强了该节点产生新连接的可能性，促使网络结构发生变化。尤其是在当尚未连接的节点对间根据相似性计算的连接可能性相同时，重要性高的节点更有可能产生新连接。根据节点的度数大小、对网络连通性的贡献作用、在网络结构中的位置以及邻居节点的重要程度等定义的中心性，均可以用来评估该节点的重要性。在一些传播网络中普遍认为，一个新加入的节点更容易选择网络中已有的大度节点建立单向行为的新连接，例如微博新用户在注册后会单方面关注明星博主。然而在现实网络中，更多的是在已有网络结构信息下，解决现存节点间产生新连接的预测问题，这种连接主要表示合作、沟通等双向行为，会受到亲密关系、传播阻塞等因素的影响。因此，一些中心性高的节点由于连接关系较为固定，不易产生新连接，反而是中心性低的节点间更容易拓展新的双向行为关系，在判断新连接产生时其节点重要性更高。

例如图1所示，A、B节点和A、C节点在相似性指标计算下的连接可能性相同，然而在现实情境下，节点重要性会从不同角度改变两个节点对间产生新连接的可能性。图1（a）表示微博关注关系网络时，C节点的度中心性小于B节点，由于A更容易去关注朋友的亲密朋友C，而不是朋友所关注的流量明星B，因此C节点对于A节点而言更重要，产生新连接可能性更大。图1（b）表示科学合作网络时，核心成员B的合作关系较为固定，产生新连接的可能性较小，反而是C节点的介数中心性更低，对同为外层成员的A而言，是建立新合作的重要伙伴，使得网络进一步扩大其连通范围。图1（c）表示机场航班网络时，B节点属于中转枢纽，当负载量达到一定程度时，与小机场A开通新航班的可能性不高，而C节点接近中心性较低，即使处于网络边缘，在新航线的备选名单中地位也格外重要。图1（d）表示涉密信息传播网络时，实心节点表示影响力较大的信息传播点，当A节点传播私密信息时，更可能会选择特征向量中心性小的C节点，认可其在信息传递过程中的重要性。

图1 4个简单加权网络示例图Fig.1 4 simple weighted network sample diagrams

综上所述，新连接的产生没有遵循可限定概率分布，利用结构相似性计算新连接可能性这一方式并不严谨，节点重要性正是通过改变这种可能性来影响连接的产生，且中心性小的节点可能更为重要。因此，FNI 算法从结构相似性和节点重要性两个角度出发，更加准确地计算新连接产生的可能性，按照可能性从高到低排序作为预测结果。

2.2 不同中心性对连接产生的影响差异

节点重要性可以影响连接产生的可能性，但是从不同角度衡量节点重要性时，影响程度也会有差异。以常用的度中心性（degree centrality，DC）、介数中心性（betweenness centrality，BC）、接近中心性（closeness centrality，CC）、特征向量中心性（eigenvector centrality，EC）为代表，在10 个经过无向加权处理后的数据集上，综合分析不同中心性对连接产生的影响差异。分别计算平均节点中心性值cˉ和平均连接中心性值-cl，二者的差值Δc可以量化表示出中心性对连接的影响程度，Δc ＞0 则说明中心性对新连接的产生具有一定影响，具体计算方式为：

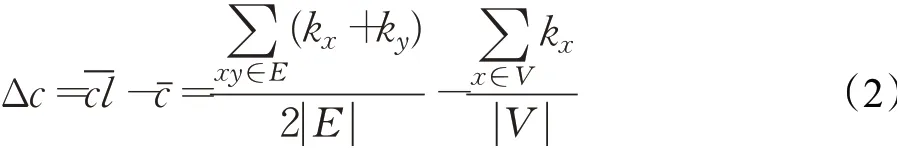
其中，kx表示节点度，E为边集合，| |E为连边数，V为节点集合，| |V为节点数。Δc越大说明该中心性对连接产生的影响越大，Δc值较小即表示对连接产生的影响不够明显。表1 展示了各数据集在不同中心性下的Δc值，括号内序号表示同一数据集上Δc值由大到小的排序。

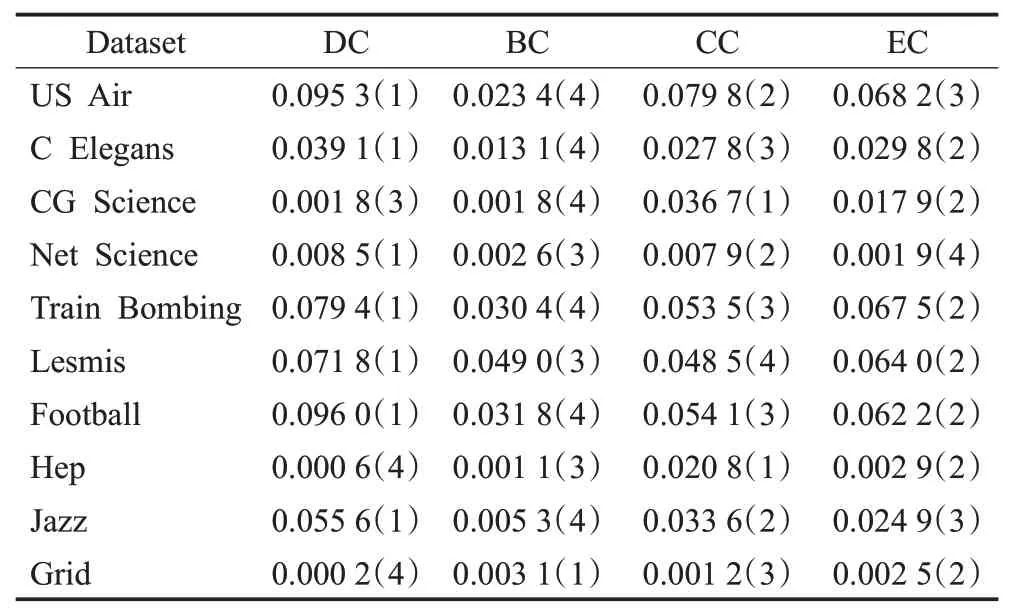
表1 各数据集上不同中心性的Δc 值Table 1 Δc values of different centrality on datasets

分析表1 可知，由于网络数据集的拓扑结构差异，不同中心性对连接产生的影响差异较大。具体表现为DC在70%的数据集上Δc值同比最高，对连接产生的影响最为明显。根据度中心性的大小来衡量节点重要性，可以有效区分各连接产生的可能性，对链路预测结果产生影响。根据表中排序顺序可知，CC 和EC 相比DC 而言总体表现相对较差，BC对连接产生的影响最小，在相似性得分相同的情况下，难以区分连接产生的可能性。因此，FNI 算法选取度中心性值来衡量节点重要性，最大程度地区分不同节点对间连接产生的可能性，充分发挥节点重要性对链路预测结果的影响作用。

2.3 FNI算法描述

通过分析节点重要性对连接产生的影响，总结出在加权网络中重要性越高的节点与其他节点建立新连接的可能性越大；通过分析不同中心性对连接产生的影响差异，总结出度中心性对连接产生的影响最大，因此提出一种融合节点重要性的无监督链路预测算法FNI。首先，通过计算边权强度simxy和路径贡献Sxy_path来计算节点对的相似性得分Sxy，并且计算节点对的中心性得分Cxy以衡量节点重要性。

其次，由于相似性得分与中心性得分的数量级存在差异，如果直接用原始数值进行分析，就会突出数值较高的一方得分在综合分析中的作用，相对削弱数值水平较低得分的作用。为了保证结果的可靠性，结合MinMaxScaler 函数对Sxy和Cxy进行归一化处理，映射到[0，1]区间，分别表示为New_Sxy和New_Cxy。

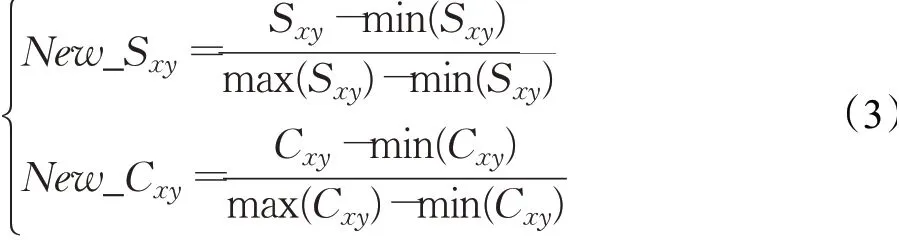
最后，由于相似性得分和中心性得分均是从衡量建立新连接可能性的角度出发，通过调节系数的方式将二者相加，实现双方共同作用的最大效益，使算法达到预测效果的最优化。对相似性得分分配系数α，对中心性得分分配系数β，计算节点对建立新连接的可能性Pxy。若系数β为负值，则表明该数据集上中心性小的节点更为重要，增加新连接产生的可能性，而中心性高的节点反而会抑制新连接的产生；若系数β为正值，则表明该数据集上节点的中心性越高，其重要性越高。如算法1所示。

算法1 FNI算法

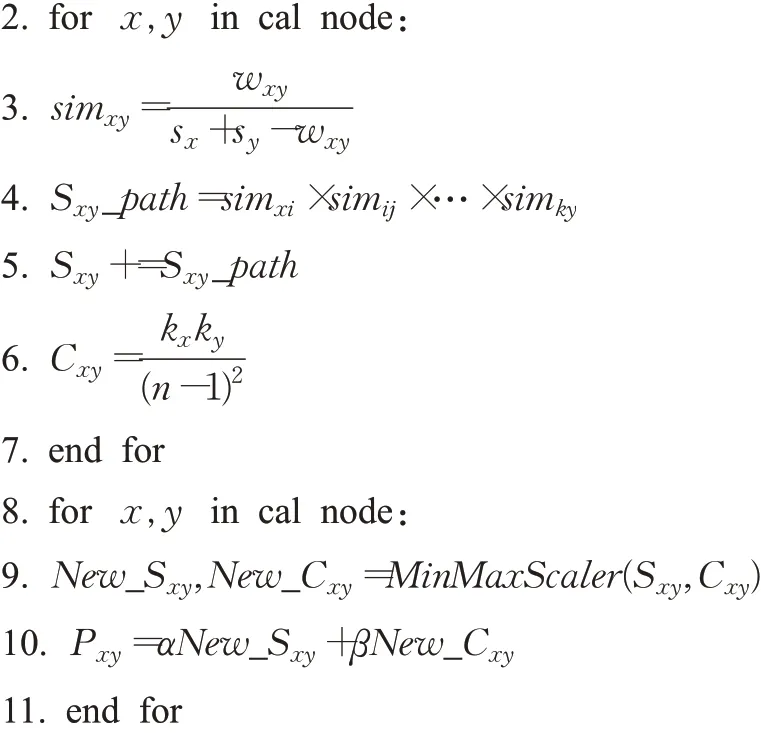
节点数量为n的网络数据集中，总节点对数量为n(n-1)/2 个。现有的基于局部结构信息的无监督预测方法均需要计算每对节点之间的相似度，时间复杂度为O(n2)。FNI算法首先计算每个节点对的相似性得分和中心性得分，时间复杂度为O(n2)；随后利用归一化函数在自定义参数下，计算节点间的连接可能性，时间复杂度仍为O(n2)。因此FNI算法的总时间复杂度为O(n2)，在保证算法运行效率的同时，综合节点重要性和结构相似性对连接产生可能性的影响，在解决小规模加权网络数据集的快速预测问题上，相比同类方法考虑更为全面。

3 实验验证与结果分析

3.1 实验设置

实验选取5个不同领域的典型真实数据集，均为小规模加权网络。将每一个数据集对应到各自需要做出快速预测结果的真实情景中，解决实际问题。美国航空公司网络US Air（US）：受天气等突发情况影响需要临时增设新航班；神经网络C Elegans（CE）：生物实验需要不断预测下一突触的产生；科学家合作网络Net Science（NS）：科学家快速锁定下一次学术合作中的预选对象；爆炸案恐怖分子联系网络Train Bombing（TB）：第一时间掌握恐怖分子间的联系倾向以便采取行动；小说人物关系网络Lesmis（LE）：即时预测小说人物间关系走向。将实验数据集预处理后按照csv 格式存储，借助可视化网络分析工具Gephi，呈现出相应数据集的网络拓扑结构图，每个网络的结构信息如表2所示。

表2 各数据集的拓扑结构Table 2 Datasets topology

采用随机抽样的方式对每个数据集进行100 次随机划分，抽取其中90%为训练集，10%为测试集，计算AUC值来表示预测结果的精确度。实验共分为以下三部分：（1）验证不同中心性对连接产生的影响差异，确保FNI 算法以度中心性衡量节点重要性的合理性；（2）横向对比其他基于局部网络结构的无监督预测方法，验证FNI 算法提高预测结果精确度的有效性；（3）纵向对比三种基于图嵌入的有监督式链路预测方法，针对小规模加权网络快速预测问题，分析FNI算法的必要性。

3.2 验证不同中心性的影响差异

不同中心性从多角度衡量节点重要性，对连接产生的影响差异很大，势必也会体现在对链路预测结果精确度的影响上。参考FNI算法的核心思想：Pxy=αNew_Sxy+βNew_Cxy，实验利用WCN、WAA、WRA 以及WLP 四种经典相似性指标计算Sxy，利用DC、BC、CC、EC四种中心性指标计算Cxy，并按照WCN 对应的新指标分别WCN_DC、WCN_BC、WCN_CC、WCN_EC 的方式，以此类推进行命名。

在实验过程中，为快速找到相应α、β值，结合梯度下降更新参数，得到最终的预测AUC 值。本次实验的重点在于证实相比其他中心性指标，度中心性度量节点重要性时，对链路预测结果具有最大程度上的积极影响。表3 总结了每一种新指标在不同数据集上的预测精确度，括号内数字代表同一数据集、不同中心性下，新指标AUC 值的排名情况，下划线标注代表预测效果不如原指标。

表3 不同中心性对预测结果AUC值的影响Table 3 Influence of different centrality on AUC values of predicted results

分析表3 可知，DC 在5 个数据集上均表现良好，能够提高原有指标1%～2%的预测精确度，在其相应20 组实验中，达到同比最高精确度12次，对连接产生的影响最大，新指标的预测结果更为精准；BC 在应用到WLP指标上时，使两个数据集下的精确度与原指标持平，除此之外其他新指标的精确度均明显下降；CC在其20组实验数据中，有3 组实验的精确度略低于原有指标，并在2 组实验上实现了预测结果最优化，总体表现相比DC 较差；EC 在TB 和LE 数据集上表现较为优异，在其20 组实验中，6 次实现最优预测结果，但在7 组实验中，大幅降低了原有指标精确度，不具有相对稳定性和普适性。

综上所述，节点重要性对连接产生具有一定的影响，其度量方式对预测结果的作用差异较大，实验结果基本符合上文理论分析。即DC相比其他三种度量方式整体对连接产生的影响最大，能够体现在链路预测的结果中，以度中心性度量节点重要性，并以此计算新连接产生的可能性，能够稳定有效地提高预测精确度。CC和EC 的影响效果波动较大，适用性弱于DC，无法解决不同结构类型数据集的链路预测问题，而BC 完全不适用。因此，在四种经典相似性指标上的大量实验，结果足以证明度中心性对新连接产生的影响最大，对链路预测结果准确性的提高效果最为明显，确保了FNI算法以度中心性大小衡量节点重要性，具有理论正确性和实践可行性。

3.3 FNI算法预测结果

针对小规模加权网络的快速预测问题，将FNI算法与同类基于局部网络结构的无监督预测方法进行横向对比实验，预测精确度结果如表4所示。

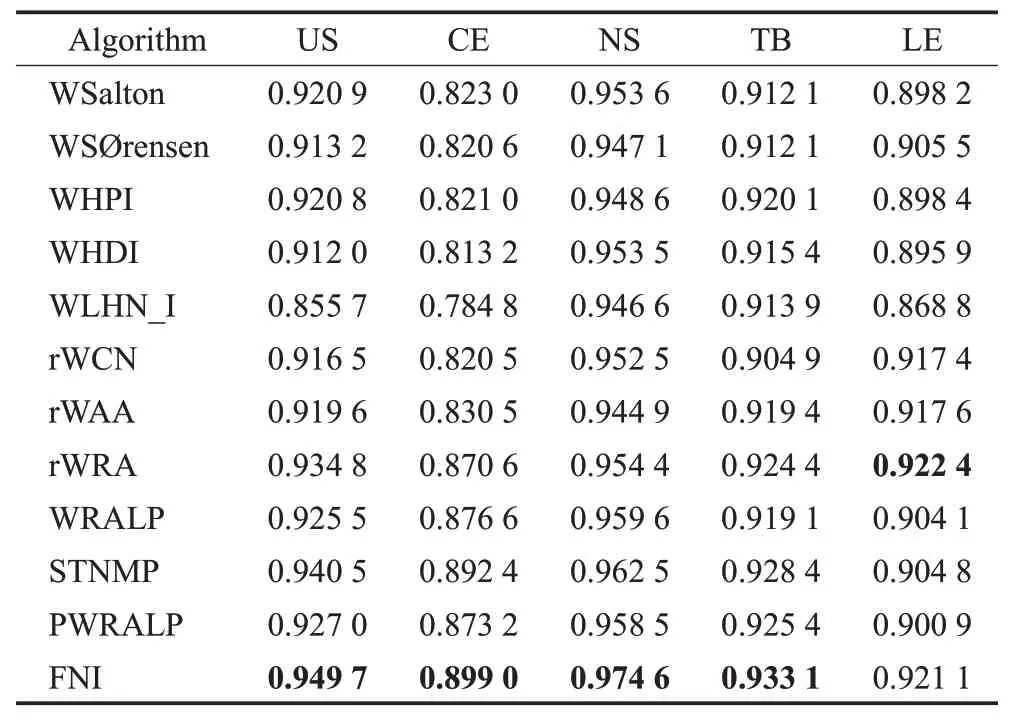
表4 FNI算法横向对比实验AUC值Table 4 AUC values of transverse contrast experiment of FNI algorithm

分析表4 可知，4 个数据集上FNI 算法预测精确度AUC 值，明显高于同类其他11 种基于局部网络结构的无监督预测方法。只有在Lesmis（LE）数据集上由于数据集特性，局部信息相比路径信息更有效，FNI 算法的精确度与rWRA指标近乎持平，但仍明显高于其他预测指标。分析其具体原因，FNI算法首先合理考虑了节点重要性对连接产生的影响；其次，利用度中心性来计算中心性得分，更加精准地计算了不同节点对间产生新连接的可能性；最后，通过自定义系数最优化结构相似性和节点重要性对预测结果的影响程度。因此，实验结果证实了在小规模加权网络数据集上，FNI算法相比现有其他同类方法整体提高了预测结果AUC 值，可以达到最佳预测效果。

在证实FNI算法预测结果的有效性后，进一步分析FNI 算法中的参数选取。在计算产生新连接可能性Pxy=αNew_Sxy+βNew_Cxy这一步骤里，参数α和参数β均为自定义参数。实验中为快速找到相应α和β值，选取α初始值为1，β初始值为-1，采用梯度下降思想来更新参数取值，将预测精确度与期望精确度差值定义为损失函数并使其最小化。图2 表示随着参数的迭代更新，各数据集上的损失Loss值不断下降，AUC值保持上升趋势，逐步趋于稳定，最终得到所需参数α、β。

图2 各数据集上Loss值和AUC值变化情况Fig.2 Loss value and AUC value changes on datasets

表5展示出FNI 算法在不同数据集上的相应参数α、β值。β在5个数据集上最终取值全部为负值，验证了中心性小的节点，在其局部网络结构中地位更加重要，与其他节点产生新连接的可能性更高。对应到5个数据的具体情境中可以理解为，航空网络里中心性大的中转枢纽可能行程较满，班次较少的小机场间更容易新建航班；神经网络里一些高中心性的神经元接受传递信息通常具有重复性，一些传递作用较少的神经元更容易传递出新信息；科学家合作网络里两个团队的权威人物间的合作概率要小于其各自同自己团队伙伴合作的概率；恐怖分子联系网络里主谋的联系关系较为隐秘固定，远离核心的帮凶间更容易彼此联系；小说人物关系网络里主要角色关系已经充分介绍，小人物间会发生更多关系碰撞的故事。

表5 FNI算法的参数取值Table 5 Parameter values of FNI algorithm

综合5个数据集上的取值表现，α稳定在区间（1.0，1.5]，β稳定在区间(-0.4,0)，说明在小规模加权网络上，结构相似性同比节点重要性对产生连接可能性的影响程度更大，但节点重要性的影响程度同样不可忽略。

FNI算法预测结果的对比实验，证实了本文的两个贡献：一是中心性小的节点反而更重要，节点重要性在链路预测问题中具有重要研究意义；二是本文提出的FNI 算法相比同类基于局部网络结构的无监督式链路预测方法，预测结果AUC值整体更高。

3.4 FNI算法的必要性评估

近年来，一些基于机器学习和深度学习的图嵌入方法在链路预测问题研究中较为常用。纵向对比无监督式FNI 算法与三种不同类型的有监督式图嵌入方法的整体性能，确保FNI 算法在当前加权网络链路预测的相关研究中具有必要性和特定优越性，实验结果如表6所示。

表6 FNI算法纵向对比实验AUC值Table 6 AUC values of longitudinal contrast experiment of FNI algorithm

由表6 可知，FNI 算法在US 数据集上相较于Node2vec 方法AUC 值提升最多，约提升27 个百分点；在NS数据集上相较于HOPE方法AUC值提升最少，约提升3 个百分点。因此，综合FNI 算法在5 个数据集上的表现，其AUC 值总体比有监督式的图嵌入方法高3～27个百分点。分析其具体原因：首先，在规模较小的数据集上监督训练的效果往往较差，稀疏网络所对应的可用特征有限，学习生成的网络表示存在较大偏差。其次，在短路径网络中，存在连接和不存在连接的嵌入向量不易区分其距离分布[25]，嵌入模型的训练效果并不理想。实验数据集除NS外，均为平均距离小于3的“小世界”网络，实验结果也表明NS数据集上图嵌入方法整体的精确度更接近于FNI算法。

针对小规模加权网络的快速预测，有监督式图嵌入方法存在一定的弊端，不仅需要额外的监督训练时间，最为主要的是其预测精确度普遍较低。FNI 算法的整体性能明显优于有监督式的图嵌入方法，故FNI算法的提出和运用具备解决实际问题的必要性。

4 结束语

节点重要性对连接产生的影响并未在现有基于局部网络结构的无监督预测方法中得到体现，并且在真实网络里中心性越小节点往往更加重要。本文从结构相似性和节点重要性两个角度计算连接可能性，提出一种融合节点重要性的无监督链路预测算法FNI。大量实验结果证明，在解决小规模加权网络的快速预测问题上，FNI 算法在同类预测方法中的预测精确度更高，且相比有监督式的链路预测方法更具研究必要性。

本文所提算法在后续研究过程中，仍有需要不断优化的方面：一是该算法虽然很好地利用中心性度量节点重要性，但是针对加权网络节点重要性的研究仍需不断探索；二是该算法在寻找路径信息时较为复杂，后续会结合降维方法，降低算法的时间复杂度，实现算法性能的进一步优化。