基于一致性原理和梯度下降法的微电网完全分布式优化调度
2022-08-19彭建伟陈博洋王晓敏刘子旭王育飞
米 阳,彭建伟,陈博洋,王晓敏,刘子旭,王育飞
基于一致性原理和梯度下降法的微电网完全分布式优化调度
米 阳,彭建伟,陈博洋,王晓敏,刘子旭,王育飞
(上海电力大学电气工程学院,上海 200090)
针对基于经典一致性算法的微电网优化调度中存在需要集中处理器对可控单元进行信息采集并做求和处理等问题,提出一种基于一致性原理和梯度下降法的完全分布式优化调度策略。该算法的一致性原理由一致项和调整项两部分组成。其中,一致项选择增量成本作为一致性算法的状态变量进行迭代计算,调整项根据功率偏差进行修正,使其满足约束条件。通过将梯度下降法和一致性原理相结合,实现微电网发电成本的优化并提高收敛速度。并且通过可控单元与相邻可控单元之间局部信息交互更新参数,应对拓扑结构的灵活变化。最后基于IEEE-14节点系统和IEEE-39节点系统仿真验证所提方法的有效性和可行性。
微电网;一致性原理;梯度下降法;完全分布式调度
0 引言
化石能源的日益枯竭,环境污染问题的日益恶化,使得国内外学者不得不研究低碳发电技术和更高效的设备,导致了分布式发电(Distributed Generation, DG)的多样化发展,包括可再生发电(Renewable Generation, RG)和分布式储能系统(Energy Storage System, ESS)[1-2]。同时由于电力系统中负荷种类的增多,柔性负荷在保持功率平衡方面也起着重要作用。因此“微电网”这一概念应运而生,其可以应对将各种DG、ESS和柔性负荷集成到电力系统中的挑战[3]。微电网有并网和孤岛两种运行模式,在孤岛模式下,为了保证微电网的安全、经济运行,需要有效协调各种发电机、储能单元以及负荷的功率平衡关系[4-6]。
微电网内部融合了大量的分布式发电单元,各种发电单元的发电特性具有多样性,且控制特性和发电成本特性也各不相同。而微电网运行调度的目标是在保证微电网整体实时功率平衡以及满足各个安全约束的同时,降低整个微电网的经济成本[7-8],根据等耗量微增率准则,经济调度的问题转化为功率分配过程中增量成本一致性的问题[9-10]。因此本文研究微电网运行调度中的实时功率分配问题,对提高微网经济性具有重要的意义。
微电网对可控单元的调控方式分为集中式和分布式两种[11-12]。集中式调控方式需要中央控制器与可控单元进行通信来获取全局信息才能对可控单元进行控制,缺乏灵活性和鲁棒性,且无法适应灵活的拓扑结构。分布式调控方式利用局部信息实现协调控制,具有计算量小、可靠性高、满足“即插即用”特性等优点[13]。
然而目前主流的基于一致性原理的分布式优化算法都需要集中处理器对可控单元进行信息采集并做求和处理以满足功率平衡。文献[14]提出了基于多智能系统的一致性模型,使得分布式算法有了理论依据。文献[15]针对面向能源互联网的多能源局域网运行调度中的实时功率分配问题,提出一种基于多智能体两层一致性理论的多能源局域网实时动态功率分配策略,但是需要1个“领导者”承担功率偏差以保持功率平衡,并不属于完全分布式计算求解。文献[16]基于一致性理论,提出一种针对自治区域的优化调度算法,通过相邻节点信息交换,更新本地参数,收敛条件为总的功率偏差,而求取功率偏差不可避免地需要对可控单元的输出功率进行求和。为了运用完全分布式算法获取全局功率不平衡信息,文献[17]将一致性理论和调频控制相结合,用一种完全分布式方法解决主动配电网功率平衡约束问题。文献[18]提出了一种基于“一致性+创新项”的分布式能源管理方法,用于协调微电网内部的可控单元,取消了集中处理器和“领导者”。
基于上述研究,本文将一致性原理与梯度下降法相结合,提出了一种改进的一致性算法实现快速收敛,减小系统功率偏差。该算法属于完全分布式算法,不依赖于集中处理器或“领导者”,各可控单元能够利用局部信息实现优化调度。通过IEEE-14节点和IEEE-39节点系统模拟微电网的运行过程,证明了算法的有效性和鲁棒性。
1 微电网调度模型
1.1 目标函数
经济调度问题是指在维持发电机、储能单元、柔性负荷和不可调节负荷有功功率平衡条件下,使系统实现经济效益的最大化。目标函数如下:
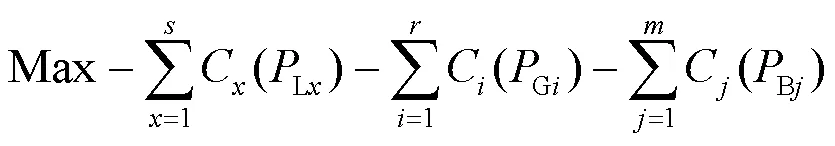
目标函数可转化为求最小值:
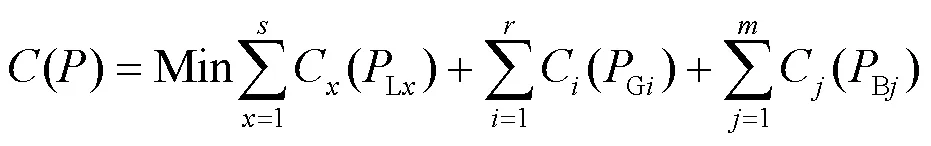
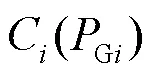

1.2 约束条件
1) 功率平衡约束

式中,为不可调度负荷。
2) 出力上、下限约束
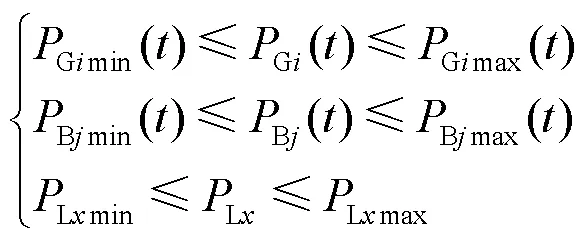
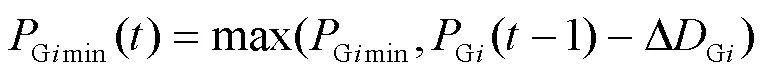
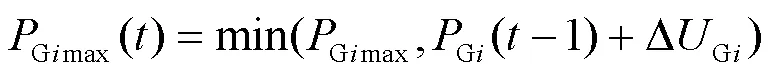


2 图论基础
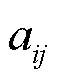
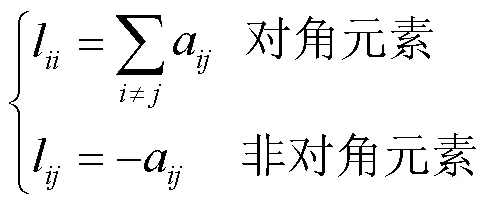
3 完全分布式优化调度
为求解上述微电网调度模型,本文提出一种基于一致性原理和梯度下降法的完全分布式算法,使其在经济上达到最优。
3.1 一致性原理
一致性算法的本质是在分布式系统中本地节点与邻接节点进行信息交互,更新本地节点的一致性变量,使得通信网络中各节点的一致性变量收敛于稳定的共同值[21]。
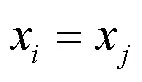
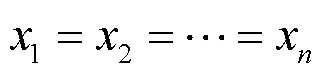
用一阶连续一致性算法可表述为
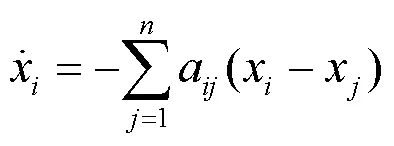
考虑到分布式电源之间的通信传输需要一定的时间,本文使用离散一致性算法来描述微电网的动态特性。离散一致性算法可表述为
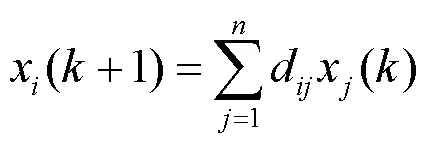

3.2 增量成本一致性计算
耗量特性曲线上某点切线的斜率为该点的耗量微增率(增量成本),本文选取增量成本作为一致性变量,增量成本的表达式为
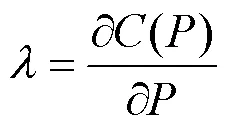
由式(3)可得

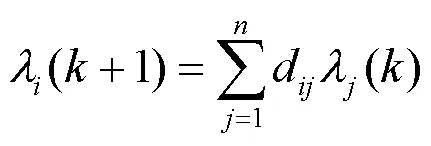
经过足够次数的迭代,系统中所有可控单元的增量成本都会收敛到一个固定值:
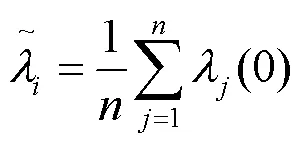

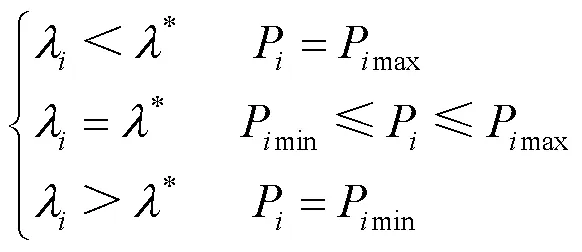
3.3 调整项的更新


在迭代计算过程中,功率调整项利用式(21)决定一致性变量的收敛方向,使得各单元的有功出力满足等式约束条件,取得最优解,证明如下。
简便起见,将式(21)写成向量形式为
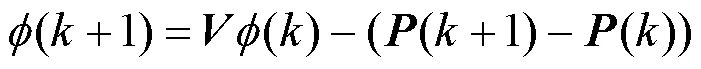
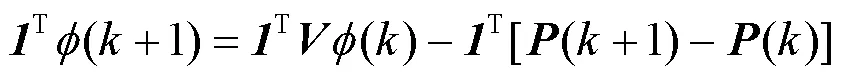
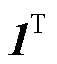

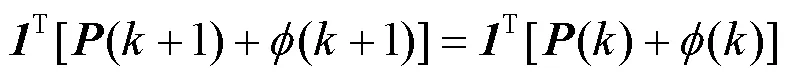
将式(25)还原成变量形式,即为
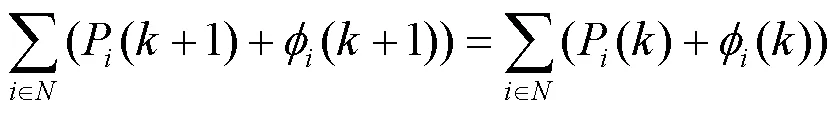
式中,为发电机、储能单元和柔性负荷总的集合。
3.4 梯度下降法
梯度下降法是一种基于函数一阶性质的优化算法,具有储存量小、结构简单、易于实现的优点。梯度的方向是函数在给定点上升最快的方向,那么梯度的反方向就是函数在给定点下降最快的方向。在最小化目标函数时,可以通过梯度下降法来一步步地迭代求解。对于目标函数为凸函数时,梯度下降法得到的结果一定是全局最优解[25]。
本文运用梯度下降优化算法—— RMSprop (Root Mean Square prop)算法,为了优化目标函数在迭代过程中存在摆动幅度过大的问题,该算法结合了经过衰减系数控制的历史梯度平方和的平方根,使得每个参数的学习率不同。效果是在参数空间更为平缓的方向,取得更大的进步,并且使得陡峭的方向变得平缓,从而加快迭代速度[26]。
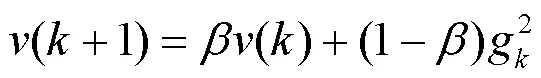
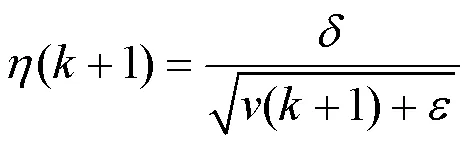

由于式(29)是集中式的可控单元功率更新原则,不属于完全分布式算法,所以需要对式(29)进行分布式改进,如式(30)—式(31)。


通过式(30)—式(31)实现了RMSprop算法的完全分布式形式。同时将RMSprop算法的梯度下降原理融入到一致性原理中,提高了算法的收敛速度,减少了算法的计算时间。
3.5 改进的完全分布式算法总流程
基于一致性原理和RMSprop算法的完全分布式优化调度算法流程如图1所示。

图1 改进的完全分布式算法流程图
具体步骤如下:
(2) 根据拓扑网络图形成Laplace矩阵,并获取状态转移矩阵和矩阵;
(3) 使用RMSprop算法更新可控单元的出力和增量成本;
(4) 根据式(20),利用一致性算法更新各可控单元的一致性状态变量即增量成本;若满足收敛条件,则得出最优解;反之则再次更新各变量。
4 仿真算例分析
为了验证所提基于一致性原理和梯度下降法的微电网完全分布式算法的有效性,本文通过Matlab软件搭建了调整后的IEEE-14节点系统和IEEE-39节点系统模拟微电网实时功率分配。由于篇幅限制,IEEE-39节点结构图略,IEEE-14节点结构图如图2所示。
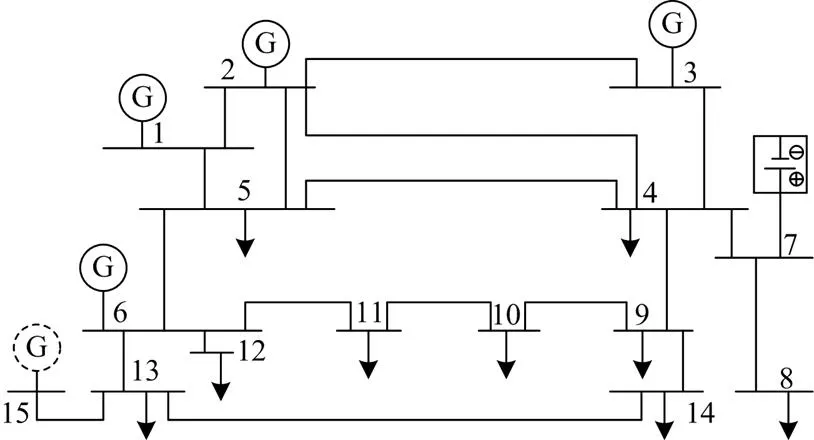
图2 IEEE-14节点系统
其中,虚线表示G15仅在4.3节中使用,节点1、2、3和6为发电机,节点7为储能单元,其余节点为柔性负荷。图2中各发电机、储能单元和柔性负荷的参数如表1所示。表中,G表示发电机,B表示储能单元,L表示柔性负荷。

表1 各类型发电机、储能单元和柔性负荷参数
4.1 增量成本一致性仿真
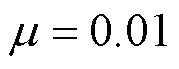
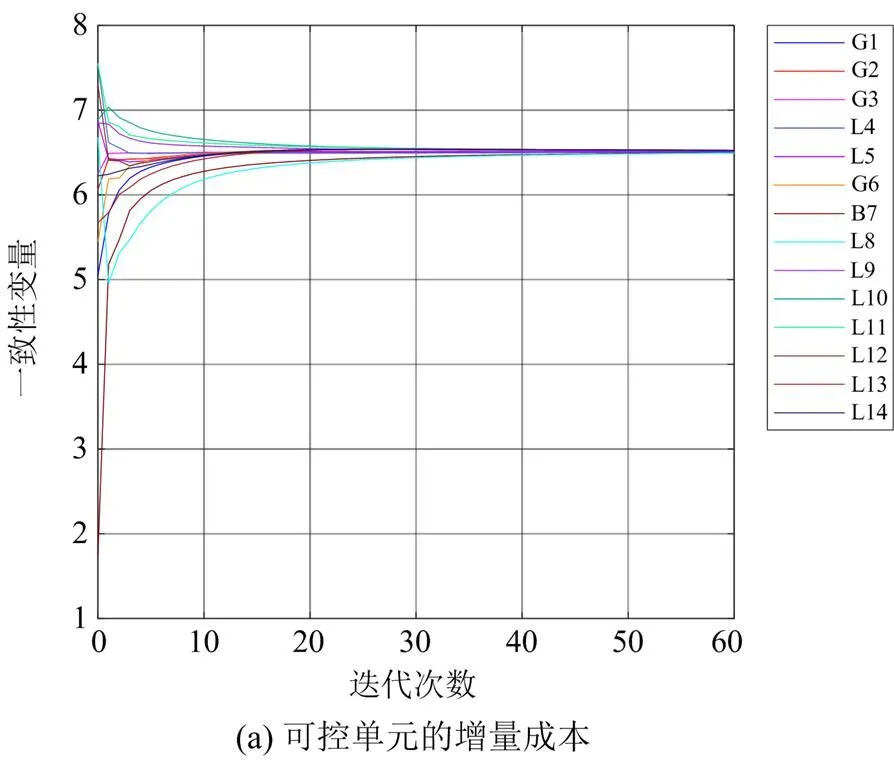
由图3(a)可知,经过60次迭代之后,算法达到收敛,系统中可控单元的一致性变量:增量成本收敛于一个共同值,且根据“等耗量微增率准则”,所得的解为最优解。由图3(b)、图3(c)可知,算法收敛时可控单元的功率输出趋于稳定,系统的不平衡功率收敛于0,满足功率平衡要求,且可控单元的功率输出均满足功率上下限要求。综上,本文提出的改进的完全分布式算法能够实现在降低可控单元发电成本条件下的功率分配。
4.2 可控单元功率越限时的增量成本一致性仿真
G3的输出功率最大值为50 kW,假设初始不平衡功率为115 kW,则可控单元的增量成本一致性收敛过程如图4所示。验证了所提算法在系统中可控单元的功率输出达到极限时的有效性。
由图4(a)、图4(b)可知,随着迭代次数的增加,柔性负荷的输出功率随之变化,发电机、储能单元的输出功率随之增加,当迭代至第4次时G3的输出功率达到上限50 kW,由式(16)可知,增量成本也达到最大值。相比于不考虑功率上、下限约束时,为了保持功率平衡,其他发电机、储能单元将承担更多的功率输出。由图4(c)可知,当算法收敛时,系统不平衡功率趋于0,所提算法在系统中可控单元的功率输出达到极限时的有效性得到证明。
4.3 可控单元即插即用时的增量成本一致性仿真
设置如下情景:仿真实验初始环境条件与4.1节相同,在算法迭代至100次时,发电机G15接入IEEE-14节点系统中,接入的位置如图2所示,算法的收敛过程如图5所示。验证了所提算法在系统中可控单元即插即用时的有效性。

由图5(a)、图5(b)可知,发电机G15接入系统后,由于其初始输出功率为0,在算法迭代的过程中其将有一定的功率输出。与未接入之前比较,其他可控单元的输出功率有所降低,可控单元的增量成本也有所降低。由图5(c)可知,虽然在迭代过程中存在一定的不平衡功率,但当算法收敛时,不平衡功率趋于0,系统功率达到平衡。因此,所提算法可以在可控单元即插即用时达到增量成本一致。
4.4 可控单元故障时的增量成本一致性仿真
微电网的运行需在可控单元发生故障退出后继续平稳运行,能够具有一定的稳定性。为了验证所提算法在可控单元故障时的有效性,设置如下情景:初始条件与上节一致,在算法迭代至100次时,发电机G1发生故障退出运行,收敛过程如图6所示。
由图6(a)、图6(b)可知,发电机G1发生故障退出运行后,输出功率由53.28 kW降为0,其承担的53.28 kW的输出功率由剩余的可控单元来承担。导致剩余的可控单元的输出功率有所提高,各可控单元的增量成本的收敛值较正常运行时也有所提高。图6(c)表明系统有功功率最终达到平衡,不平衡功率为0,验证了所提算法在可控单元故障时的有效性。
4.5 多次调度指令增量成本一致性仿真
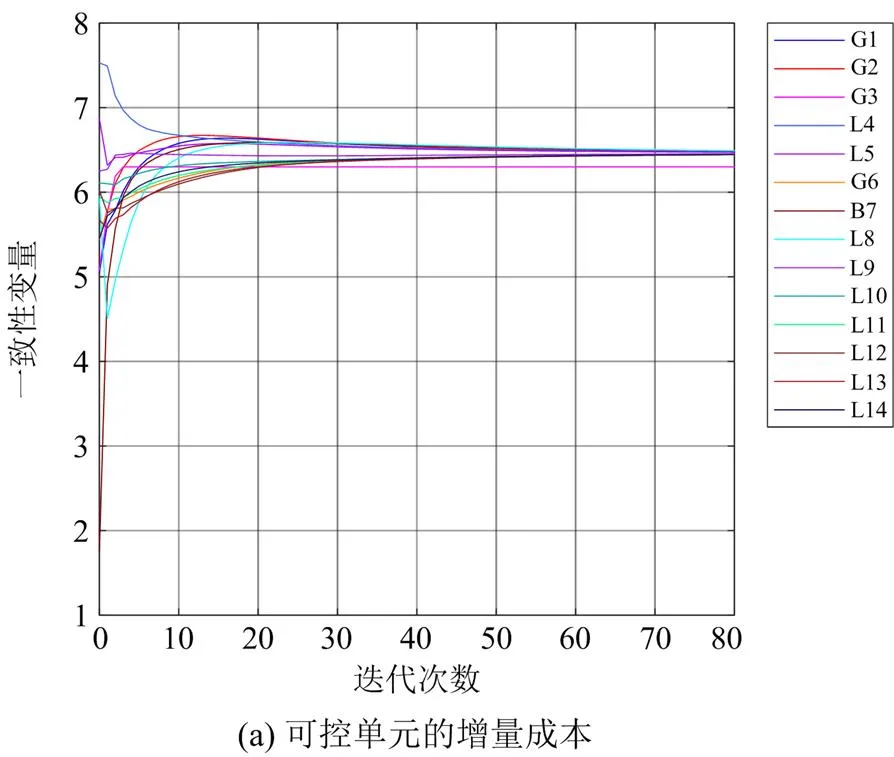
实际上,不平衡功率是实时变化的,导致调度指令也随之发生变化。因此,为了验证所提算法的实时性,将不平衡功率依次设置为20 kW、36.8 kW、64.2 kW,算法的收敛过程如图7所示。

由图7(a)、图7(b)可以看出,当不平衡功率变化时,所有可控单元的增量成本最终均能趋于一致,且随着不平衡功率的增加,各可控单元的增量成本也逐渐增加,各发电机的出力均能趋于稳定;由图7(c)可以看出,不平衡功率最终收敛到0,所提算法可以满足基本的多次调度指令要求。
4.6 与传统算法的对比仿真
为了验证所提算法在迭代效率上比传统算法更高,该小节使用两种较为常见的传统算法来解决4.1节的问题,即初始不平衡功率为20 kW,算法的收敛条件均不变。通过比较不平衡功率在迭代过程中的变化,来反映各个算法的迭代效率,对比结果如图8所示。

图8 三种算法的不平衡功率
曲线1表示使用传统集中式算法求解的不平衡功率的收敛过程;曲线2表示使用经典一致性算法求解的不平衡功率的收敛过程;曲线3表示使用本文所提出的基于一致性原理和梯度下降法的完全分布式算法求解的不平衡功率的收敛过程。
由图8可知,曲线1迭代100次后收敛,计算时间为0.732 s;曲线2迭代86次后收敛,计算时间为0.623 s;曲线3迭代60次后收敛,计算时间为0.417 s。由此可得,本文所提出的基于一致性原理和梯度下降法的完全分布式算法相比于其他算法减少了计算时间,效率也更高。
4.7 IEEE-39节点增量成本一致性仿真
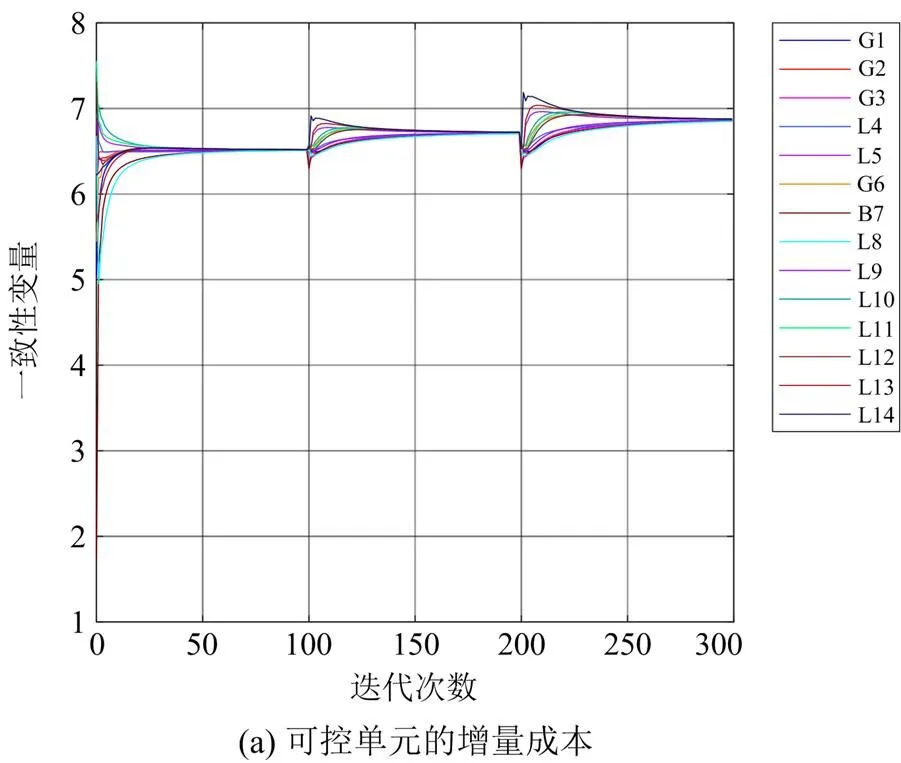
建立IEEE-39节点仿真系统的目的是验证所提算法在含有大量可控单元的微电网中的有效性。假设初始不平衡功率为170 kW,算法的收敛过程如图9所示。
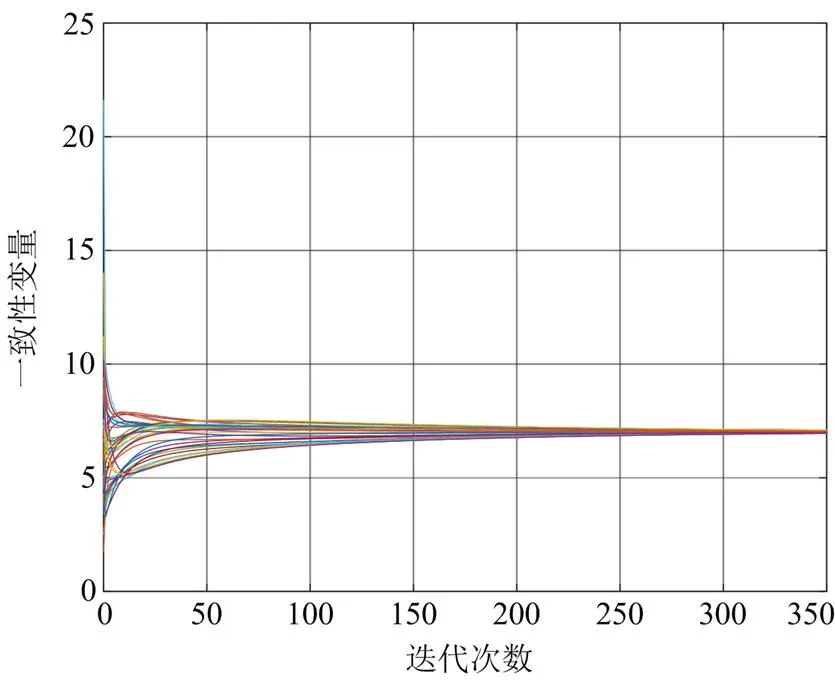
图9 IEEE-39节点的增量成本一致性收敛过程
由图9可知,算法在迭代350次时达到收敛,系统中各可控单元的增量成本收敛于一个共同值,且根据“等耗量微增率准则”,共同值为最优解。因此,所提算法在含有大量可控单元的微电网中的有效性得到证明。
5 结论
本文提出了一种基于一致性原理和梯度下降法的完全分布式算法,用于研究微电网的功率分配问题。该方法主要有以下优势:
(1) 相比于集中调控方式,完全分布式调控方式中的可控单元仅需其本地和相邻可控单元的信息,利用局部信息实现优化调度,并且能够应对拓扑结构的灵活变化。
(2) 通过将梯度下降法与一致性原理相结合,有效地减少了迭代次数,提高了算法的收敛效率。
(3) 以可控单元的增量成本作为一致性变量设计完全分布式算法,在保证功率平衡的基础上对可控单元的输出功率进行合理分配,优化微电网的运行成本。
在微电网优化调度的后续研究工作中,将继续考虑非凸目标函数(考虑阀点效应)、潮流约束、信息安全等因素。
[1] 伍也凡, 刘浩田, 肖振锋, 等. 考虑源-网-荷不确定性的增量配电网规划研究综述[J]. 电力系统保护与控制, 2021, 49(8): 177-187.
WU Yefan, LIU Haotian, XIAO Zhenfeng, et al. Review of incremental distribution network planning considering the uncertainty of source-network-load[J]. Power System Protection and Control, 2021, 49(8): 177-187.
[2] 张立辉, 戴谷禹, 聂青云, 等. 碳交易机制下计及用电行为的虚拟电厂经济调度模型[J]. 电力系统保护与控制, 2020, 48(24): 154-163.
ZHANG Lihui, DAI Guyu, NIE Qingyun, et al. Economic dispatch model of virtual power plant considering electricity consumption under a carbon trading mechanism[J]. Power System Protection and Control, 2020, 48(24): 154-163.
[3] LIU Guodong, JIANG Tao. Resilient distribution system leveraging distributed generation and microgrids: a review[J]. IET Energy Systems Integration, 2020, 2(4): 289-304.
[4] 李咸善, 董鑫, 程杉, 等. 微电网群频率调整的分层协调控制策略[J]. 电力系统保护与控制, 2020, 48(21): 1-14.
LI Xianshan, DONG Xin, CHENG Shan, et al. Hierarchical coordinated control strategy for frequency adjustment of microgrid groups[J]. Power System Protection and Control, 2020, 48(21): 1-14.
[5] MURTY V, ASHWANI K. Multi-objective energy management in microgrids with hybrid energy sources and battery energy storage systems[J]. Protection and Control of Modern Power Systems, 2020, 5(1): 1-20.
[6] 王植, 马振, 胡鹏涛, 等. 孤岛交直流混合微电网功率互助策略[J]. 电力建设, 2021, 42(1): 76-84.
WANG Zhi, MA Zhen, HU Pengtao, et al. Mutual power support strategy for isolated hybrid AC/DC microgrid[J]. Electric Power Construction, 2021, 42(1): 76-84.
[7] 周烨, 汪可友, 李国杰, 等. 基于多智能体一致性算法的微电网分布式分层控制策略[J]. 电力系统自动化, 2017, 41(11): 142-149.
ZHOU Ye, WANG Keyou, LI Guojie, et al. Distributed hierarchical control for microgrid based on multi-agent consensus algorithm[J]. Automation of Electric Power Systems, 2017, 41(11): 142-149.
[8] 杨毅, 雷霞, 叶涛, 等. 考虑安全性与可靠性的微电网电能优化调度[J]. 中国电机工程学报, 2014, 34(19): 3080-3088.
YANG Yi, LEI Xia, YE Tao, et al. Microgrid energy optimal dispatch considering the security and reliability[J]. Proceedings of the CSEE, 2014, 34(19): 3080-3088.
[9] 谢俊, 陈凯旋, 岳东, 等. 基于多智能体系统一致性算法的电力系统分布式经济调度策略[J]. 电力自动化设备, 2016, 36(2): 112-117.
XIE Jun, CHEN Kaixuan, YUE Dong, et al. Distributed economic dispatch based on consensus algorithm of multi agent system for power system[J]. Electric Power Automation Equipment, 2016, 36(2): 112-117.
[10] 杨家豪. 基于一致性算法的孤岛型微电网群实时协同功率分配[J]. 电力系统自动化, 2017, 41(5): 8-15, 38.
YANG Jiahao. Consensus algorithm based real-time collaborative power dispatch for island multi- microgrid[J]. Automation of Electric Power Systems, 2017, 41(5): 8-15, 38.
[11] 张孝顺, 余涛. 互联电网AGC功率动态分配的虚拟发电部落协同一致性算法[J]. 中国电机工程学报, 2015, 35(15): 3750-3759.
ZHANG Xiaoshun, YU Tao. Virtual generation tribe based collaborative consensus algorithm for dynamic generation dispatch of AGC in interconnected power grids[J]. Proceedings of the CSEE, 2015, 35(15): 3750-3759.
[12] 李方圆. 基于多智能体协同算法的智能电网分布式调度与优化[D]. 合肥: 中国科学技术大学, 2019.
LI Fangyuan. On distributed operation and optimization in smart grid: an MAS coordination algorithm-based approach[D]. Hefei: University of Science and Technology of China, 2019.
[13] 乐健, 周谦, 赵联港, 等. 基于一致性算法的电力系统分布式经济调度方法综述[J]. 电力自动化设备, 2020, 40(3): 44-54.
LE Jian, ZHOU Qian, ZHAO Liangang, et al. Overview of distributed economic dispatch methods for power system based on consensus algorithm[J]. Electric Power Automation Equipment, 2020, 40(3): 44-54.
[14] OLFATI S, Fax A, MURRAY R. Consensus and cooperation in networked multi-agent systems[J]. Proceedings of the IEEE, 2007, 95(1): 215-233.
[15] 米阳, 刘红业, 宋根新, 等. 面向能源互联网的多能源局域网两层功率优化分配[J]. 电力自动化设备, 2018, 38(7): 1-10.
MI Yang, LIU Hongye, SONG Genxin, et al. Two-layer power optimization allocation of multi-energy local networks oriented to energy internet[J]. Electric Power Automation Equipment, 2018, 38(7): 1-10.
[16] 蒲天骄, 刘威, 陈乃仕, 等. 基于一致性算法的主动配电网分布式优化调度[J]. 中国电机工程学报, 2017, 37(6): 1579-1590.
PU Tianjiao, LIU Wei, CHEN Naishi, et al. Distributed optimal dispatching of active distribution network based on consensus algorithm[J]. Proceedings of the CSEE, 2017, 37(6): 1579-1590.
[17] 边晓燕, 孙明琦, 赵健, 等. 基于一致性算法的源-荷协同分布式优化调控策略[J]. 中国电机工程学报, 2021, 41(4): 1334-1347, 1540.
BIAN Xiaoyan, SUN Mingqi, ZHAO Jian, et al. Distributed coordinative optimal dispatch and control of source and load based on consensus algorithm[J]. Proceedings of the CSEE, 2021, 41(4): 1334-1347, 1540.
[18] HUG G, KAR S, WU C. Consensus + innovations approach for distributed multiagent coordination in a microgrid[J]. IEEE Transactions on Smart Grid, 2015, 6(4): 1893-1903.
[19] 李坚, 吴亮红, 张红强, 等. 基于排序交叉优化算法的冷热电联供微电网经济调度[J]. 电力系统保护与控制, 2021, 49(18): 137-145.
LI Jian, WU Lianghong, ZHANG Hongqiang, et al. Microgrid economic dispatch of combined cooling, heating and power based on a rank pair learning crisscross optimization algorithm[J]. Power System Protection and Control, 2021, 49(18): 137-145.
[20] 张靠社, 冯培基, 张刚, 等. 考虑源荷不确定性的CCHP型微网多目标优化调度[J]. 电力系统保护与控制, 2021, 49(17): 18-27.
ZHANG Kaoshe, FENG Peiji, ZHANG Gang, et al. Multi-objective optimization scheduling of CCHP-type microgrids considering source-load uncertainty[J]. Power System Protection and Control, 2021, 49(17): 18-27.
[21] 刘青, 赵洋, 李宁, 等. 基于分布式神经动力学算法的微电网多目标优化方法[J]. 电力系统保护与控制, 2021, 49(11): 105-114.
LIU Qing, ZHAO Yang, LI Ning, et al. Multiple objective optimization of a microgrid based on a distributed neural dynamics algorithm[J]. Power System Protection and Control, 2021, 49(11): 105-114.
[22] YANG Shiping, TAN Sicong, XU Jianxin. Consensus based approach for economic dispatch problem in a smart grid[J]. IEEE Transactions on Power Systems, 2013, 28(4): 4416-4426.
[23] XU Yinliang, ZHANG Wei, HUG G, et al. Cooperative control of distributed energy storage systems in a microgrid[J]. IEEE Transactions on Smart Grid, 2015, 6(1): 238-248.
[24] XU Yinliang, LI Zhicheng. Distributed optimal resource management based on the consensus algorithm in a microgrid[J]. IEEE Transactions on Industrial Electronics, 2015, 62(4): 2584-2592.
[25] 杨珺, 侯俊浩, 刘亚威, 等. 分布式协同控制方法及在电力系统中的应用综述[J]. 电工技术学报, 2021, 36(19): 4035-4049.
YANG Jun, HOU Junhao, LIU Yawei, et al. Distributed cooperative control method and application in power system[J]. Transactions of China Electrotechnical Society, 2021, 36(19): 4035-4049.
[26] 马锴, 于洋庆, 朱善迎, 等. 基于梯度下降和一致性的电网分布式经济调度算法[J]. 中国科学: 信息科学, 2018, 48(10): 1364-1380.
MA Kai, YU Yangqing, ZHU Shanying, et al. Distributed algorithm for economic dispatch based on gradient descent and consensus in power grid[J]. Scientia Sinica: Informationis, 2018, 48(10): 1364-1380.
Fully distributed optimal dispatch of a microgrid based on consensus principle and gradient descent
MI Yang, PENG Jianwei, CHEN Boyang, WANG Xiaomin, LIU Zixu, WANG Yufei
(College of Electrical Engineering, Shanghai University of Electric Power, Shanghai 200090, China)
There are problems with the classical consensus algorithm in microgrid optimal dispatching in that it requires a centralized processor to collect and sum the information of the controllable units. Thus a completely distributed optimal scheduling strategy based on a consensus algorithm and gradient descent is proposed. The consensus principle of the algorithm consists of two parts: a consensus term and an adjustment term. The consensus term selects incremental cost as the state variable for iterative calculation. The adjustment term is corrected according to the power deviation to meet the constraints. This paper combines the gradient descent with the consensus principle to optimize the power generation cost of the microgrid and improve the convergence speed. In addition, the parameters can be updated through local information interaction between the controllable unit and the adjacent controllable unit to flexibly cope with a change of topology. Finally, the effectiveness and feasibility of the proposed method are verified by system simulation results of IEEE-14 nodes and IEEE-39 nodes.
microgrid; consensus principle;gradient descent; fully distributed dispatch
10.19783/j.cnki.pspc.211371
国家自然科学基金面上项目资助(61873159);上海市自然科学基金(22ZR1425500)
2021-10-11;
2021-11-22
米 阳(1976—),女,通信作者,博士,教授,研究方向为微网控制、电力系统稳定运行与控制等;E-mail: miyangmi@163.com
彭建伟(1998—),男,硕士研究生,研究方向为电力系统优化调度;E-mail: 1774669400@qq.com
陈博洋(1997—),男,硕士研究生,研究方向为综合能源微网群运行优化。E-mail: 646621959@qq.com
This work is supported by the General Program of National Natural Science Foundation of China (No. 61873159).
(编辑 魏小丽)
