基于GAM的鞍山气象条件对PM2.5和SO2的影响研究

刘 朋，马海搏，陈正元

(河南省地质局生态环境地质服务中心，河南 郑州 450053)

0 引 言

鞍山市(40°27′～41°34′，122°10′～123°41′)位于中国东北地区，是中国重要的钢铁工业基地。由于铁矿、岫岩、玉石矿等矿产资源的开发，大量大气污染物进入空气，对城市空气质量造成了影响。疫情期间，虽然人类生产生活活动大幅减少，但当不利气象条件发生之际依然会引发空气质量预警。因此，气象因子也是影响城市空气质量的关键因素[1]。而城市空气质量也成为政府相关部门、国内外学者关住的焦点问题[2-3]。在以往的研究中，多通过对数据进行回归分析或构建对应模型，根据数据变化趋势定性分析气象因子对城市大气污染物的影响[4-5]。为定量分析气象因子对大气污染物浓度变化的影响，本研究通过收集2019年全年鞍山市大气污染物数据、气象数据，在考虑城市大气污染物浓度本底值、季节变化等混杂因素的同时，以PM2.5、SO2两类大气污染物为例，利用广义可加模型(GAM)构建鞍山市城市气象因子对大气污染物影响效应的模型，并引入相对危险度(RR)的概念，计算定量关系，最终为城市发展规划、大气污染管理等提供理论依据。

1 数据与方法

1.1 数据来源

本文通过GAM构建了鞍山市气象因子与大气污染物间的响应关系，其中气象数据采用国家气候信息中心(http://data.cma.cn/)54339号气象站点的2019年全年数据，包括逐时风速、温度、相对湿度等多项数据，大气污染物浓度数据采用1753A号站点监测到的2019年全年逐时PM2.5及SO2浓度数据。

1.2 方法

1.2.1 广义可加模型

广义可加模型(Generalized Additive Model，GAM)是广义线性模型(Generalized Linear Model，GLM)的半参数拓展[6-7]，适用于各种不同类型分布的函数分析，可直接拟合响应变量和多个解释变量间的非线性关系，在控制混杂因素、对不同函数进行加和的同时也降低了线性设定带来的模型风险[8-9]。GAM的一般形式如下：

(1)

式(1)中:g(μi)为连接函数，且二次可导；fj(Xj)则代表各种非参数平滑函数，即解释变量；p为解释变量个数；a为截距。

1.2.2 模型构建

在构建模型之初，需首先确定响应变量的分布方式。本研究采用频次直方图的形式分析大气污染物数据，得出响应变量的分布特征，以大致确定其连接函数(表1)。其次，为更全面地分析气象因子对大气污染物的影响，本研究选取多种气象因子作为解释变量带入模型，考虑到过多的解释变量可能导致模型的多重共线性问题，本研究采用方差膨胀因子(variance inflation factor，VIF)来评价解释变量之间的相关关系，通过VIF值筛选气象因子。当VIF值越接近于1，多重共线性越轻，反之越重；当VIF值大于10时，回归模型则存在严重的多重共线性。综合前人研究成果，最终选择VIF检验的临界值为3，VIF大于3的解释变量将被移除[10-11]。

表1 响应变量分布和连接函数

同时，城市大气污染物浓度本底值是影响城市大气污染物含量变动的重要原因，也是影响模型结果可靠性的重要混杂因素。考虑到大气污染可能存在滞后性，为获取合适的城市尺度大气污染本底值代替数据，本研究通过拉长污染物数据时间步长，并分别将污染物小时数据对应的当日污染物日平均浓度数据、提前1～7 d的日均数据、本周及提前一周的污染物浓度平均数据分别带入模型，选择模型AIC值最小时所对应的数据，确定最佳的代替城市大气污染本底值数据[12-14]。除此之外，本研究也将季节、月份变化作为混杂因素带入模型，以增加模型结果的可靠性。

1.2.3 定量关系计算

以PM2.5与SO2两类大气污染物浓度变化为响应变量，筛选出的气象因子为解释变量，探索鞍山市两类大气污染物浓度与气象因子之间的响应关系。同时引入流行病学中常用的相对危险度(relative risk,RR)的概念，结合GAM模型构建出气象因子与大气污染物间的响应关系，计算各气象因子每发生单位变化时所对应大气污染物浓度的相对改变量[15-16]。由此得到RR及其95%的置信区间(95%CI)详见式(2)和式(3)：

RR=exp(β×ΔX)

(2)

RR(95%CI)=exp[(β±1.96SE)×ΔX]

(3)

式中，β为回归系数，ΔX为气象因子的单位变化量，SE为标准误差。

在其他混杂因子保持不变的条件下，结合RR进一步计算出大气污染物浓度改变的百分率。当气象因子在阈值范围内变化ΔX单位时，大气污染物改变的百分率(ER%)及其95%的置信区间(95%CI)详见式(4)和式(5)：

ER%=(RR-1)×100%

(4)

ER%(95%CI)=(exp[(β±1.96SE)
×ΔX]-1)×100%

(5)

2 结果与讨论

本研究通过SPSS工具计算三类气象因子间的VIF值。由表2计算结果可知，当响应变量分别为PM2.5、SO2时，对应三类气象因子VIF(方差膨胀因子)值均小于设定阈值。因此当响应变量为PM2.5或SO2时，温度、风速、相对湿度三类气象因子可作为解释变量同时带入模型。

表2 气象因子间VIF值

将PM2.5与SO2不同滞后天数、不同时间步长的数据分别带入模型后，得出模型的AIC值(表3)。由模型AIC值可知，随着滞后天数的增加模型AIC值增加，且日均数据明显优于周均数据。因此，本研究最终选取当天的PM2.5、SO2日均数据作为城市污染本底值，并作为混杂因素带入模型。同时，将季节、月份等变化也作为混杂因素带入模型，分别构建PM2.5和SO2对温度、风速、相对湿度的响应关系，详见图1。

表3 大气污染物浓度滞后数据对应模型AIC值

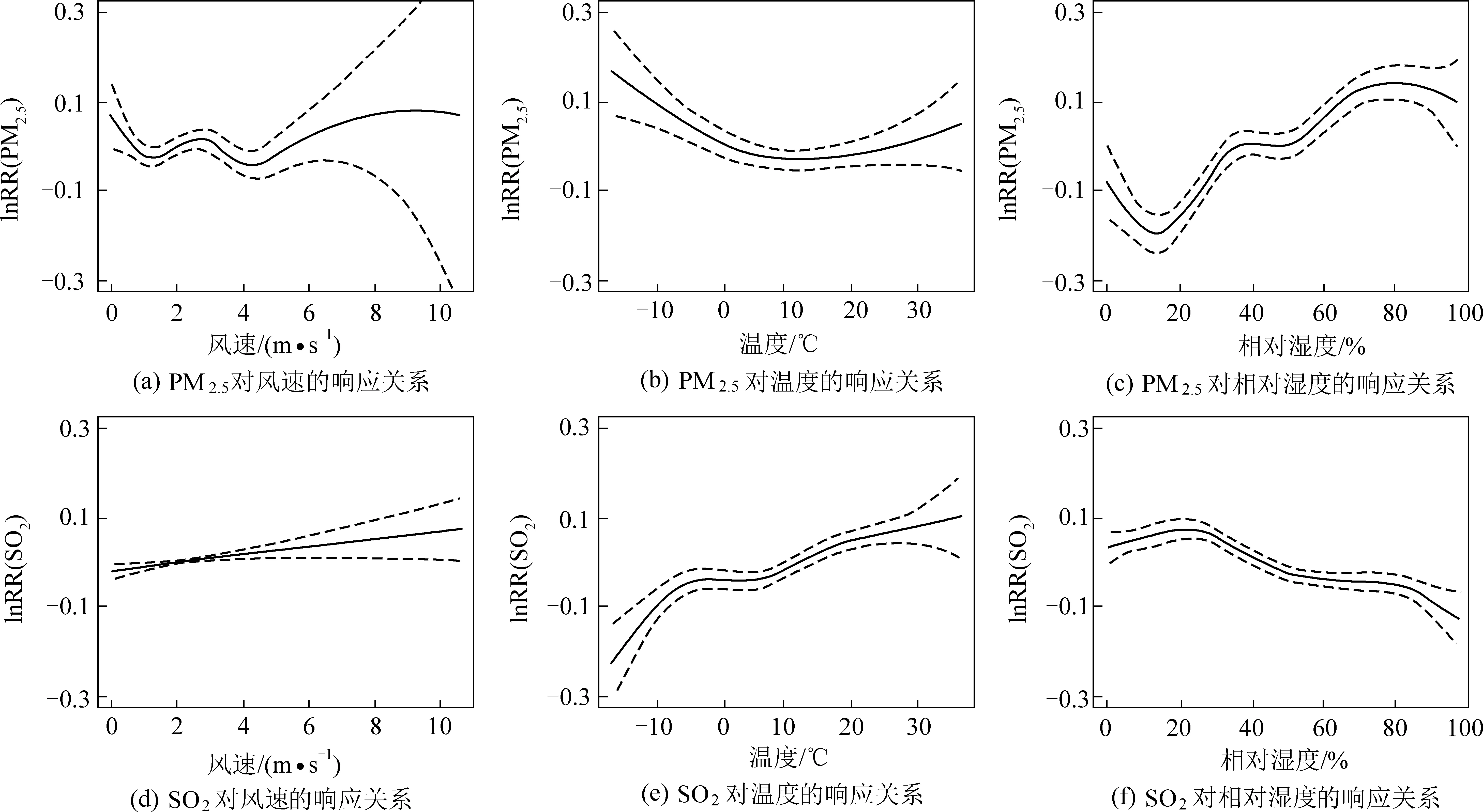
图1 两类大气污染物浓度对三类气象因子的响应关系图Fig.1 Response relationship between the concentrations of two types of air pollutants and three types of meteorological factors

根据图1所构建的气象因子与大气污染物浓度间的响应关系，通过哑变量对数据进行分类，计算各类气象因子在不同阈值区间内变化时所引起的大气污染物浓度的改变百分率(表4)。

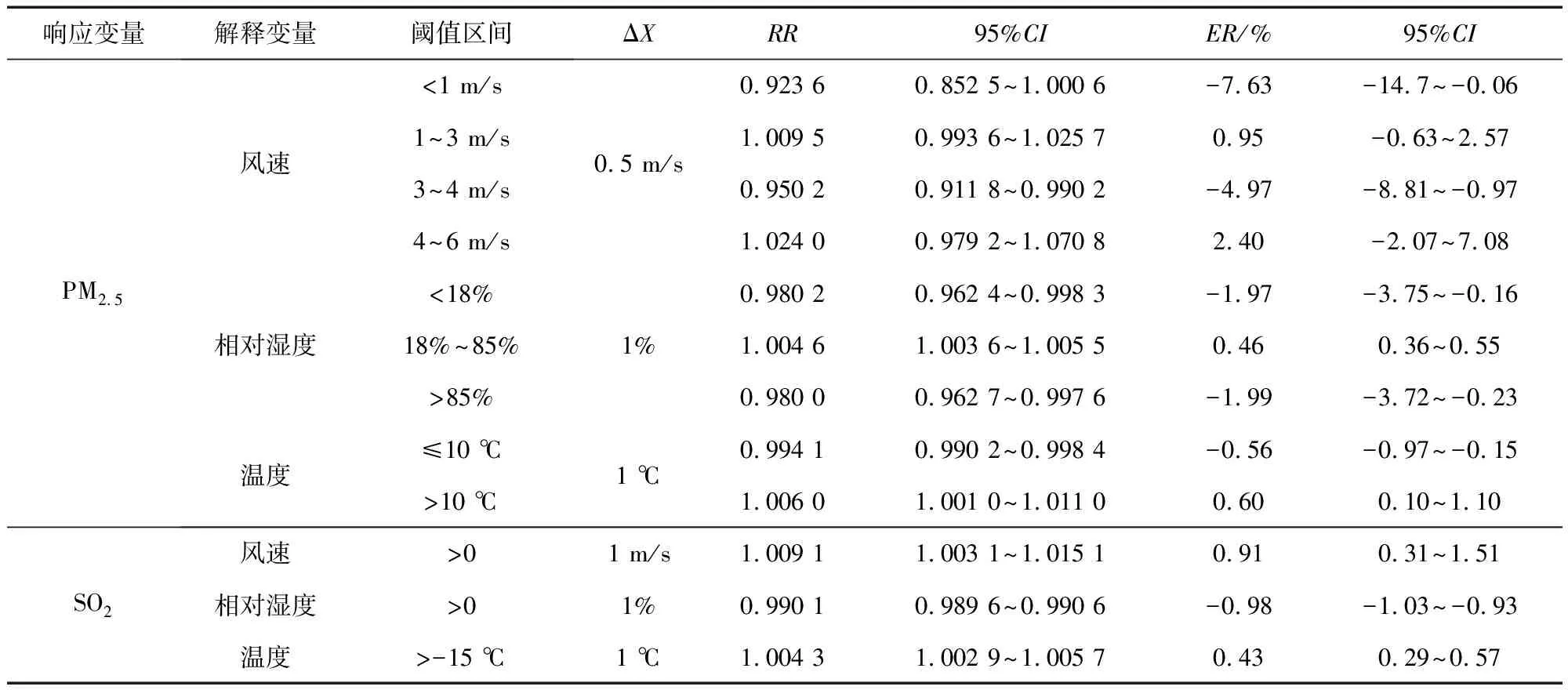
表4 气象因子对大气污染物浓度的定量影响

结合图1与表4所计算的定量关系可知，当响应变量为PM2.5时，随风速的增加PM2.5浓度整体呈波浪式变化，并非简单的风速大PM2.5浓度低、风速低PM2.5浓度高。当风速在小于1 m/s和3～4 m/s区间变化时，风速的增加对PM2.5呈净化作用，且风速每增加0.5 m/s，PM2.5浓度最大改变量为减小7.36%。当风速在2～3 m/s或3～6 m/s之间变化时，风速越高，PM2.5浓度越高，相对改变量最高为2.49%。风速在4～6 m/s区间内升高导致PM2.5浓度升高的原因可能为过高的风速将地表浮沉吹起，从而导致PM2.5浓度升高。当风速大于6 m/s时，对应置信区间过大，其模型结果可信度较低，故不做定量计算。

温度对PM2.5的影响也存在明显的阈值效应，阈值在10 ℃左右，使PM2.5浓度随温度的增加先减小后增加。在温度低于约10 ℃时，PM2.5浓度随温度每升高一个单位变化量的相对改变量为-0.56%，当温度高于10 ℃时，PM2.5浓度随温度每升高一个单位变化量的相对改变量为0.6%。其中在小于10 ℃阈值范围内温度越低PM2.5浓度越高的原因可能是冬季取暖造成的。

在相对干燥的天气条件下(相对湿度<18%)或降雨时(相对湿度>85%)，相对湿度的增加多对PM2.5的净化起到积极作用，且相对湿度每增加一个单位的变化量PM2.5浓度的相对改变量为-1.97% 与-1.99%。而在18%～85%区间内，相对湿度的增加多引起PM2.5浓度的升高，对应改变量为0.46%。

当响应变量为SO2时，三类气象因子的影响效应相对简单，当解释变量为风速或温度时，SO2浓度随解释变量的增加而增加，呈正相关关系。风速与温度增加一个ΔX，SO2浓度相对改变量分别为0.91%与0.43%。当解释变量为相对湿度时，SO2随相对湿度的增加而降低，呈负相关关系，对应改变量为-0.98%。

3 结 论

本研究通过广义可加模型，在考虑城市大气污染排放、月份变化等混杂因素的情况下，对大气污染物与气象因子建立响应关系。在引入RR值的概念后，通过定量计算，定量分析了鞍山市气象因子(风速、温度、相对湿度)对PM2.5与SO2两种大气污染物的影响。最终得出以下结论：

(1)风速、温度、相对湿度三类气象因子对PM2.5的影响均存在阈值效应。解释变量为风速时，随着风速的增加PM2.5浓度呈先减小—再增加—再减小—再增加的波浪式变化，阈值分布在1、3、4、6 m/s；解释变量为温度时，使PM2.5浓度随温度的升高先增加后减小，阈值在10 ℃左右；解释变量为相对湿度时，在干燥条件下或降雨时，PM2.5随相对湿度的增加而降低，阈值分布在18%、85%。

(2)风速在0～1 m/s与3～4 m/s区间时对PM2.5的净化起到积极作用，且风速在0～1 m/s区间内对PM2.5的净化效果最强，风速每升高0.5 m/s，PM2.5浓度的相对改变量为-7.63%。相对湿度则在大于85%时对PM2.5的净化效果最强，相对湿度每增加1%对应PM2.5浓度的相对改变量为-1.99%。当温度低于10 ℃时，温度的增加对PM2.5的净化起到积极作用，温度每增加1 ℃，PM2.5浓度的相对改变量为-0.56%。

(3)三类气象因子的变化对SO2浓度的影响没有明显的阈值效应，SO2浓度与温度、风速呈正相关，与相对湿度呈负相关。即在高温大风天气条件下，城市越易发生SO2类型污染，或在干燥条件下，城市越易发生SO2类型污染。相对来说，低风低温及高湿天气条件对SO2的净化起到积极作用。风速、温度、相对湿度三类气象因子每发生单位减小量对应SO2浓度的相对改变量分别为-0.91%、-0.43%和0.98%。