地震作用下混凝土水池结构动力响应研究

2022-08-19张文斌朱正瑜

西安科技大学学报 2022年4期

张文斌，朱正瑜

(西北工业大学基建处，陕西西安 710072)

0 引言

中国是地震多发性国家。在京津冀、长三角和珠三角城市群人口、财富高度集中地区，都曾多次发生6级以上强震。随着时代的发展，钢筋混凝土水池结构越来越广泛的应用于实际工程中，特别是重大工程中，像泳池、实验水池、渡槽等水池结构以及类似的储液装置越来越常见。大多数混凝土水池密集兴建于近20年，尚未经历过强震的考验，大量混凝土水池或多或少都面临一定程度的地震威胁[1]。福岛核电站由于地震后引发海啸致使二次供水系统失效，从而间接引发了核泄露，薛志成等人提出为了不重蹈日本福岛核事故之覆辙，将储存核电厂海水淡化区域大量淡水的工业水池系统作为核电厂应急水源，并将储水池进行抗震设计的构想[2-5]。

钢筋混凝土水池在地震力作用下，周围土体与池内的液体会对池壁产生液固耦合(FSI)现象以及土与结构相互作用(SSI)[6-8]。FSI问题是研究液体与固体两相介质之间的交互作用的问题。刘洁平等人研究地震力对混凝土水池的作用时，发现在地震作用下，高而柔的大型水池中的水产生晃动，由于池壁相对较柔，水的质量相对池身较大，甚至超过了水池本身重量，产生的动水压力和冲击压力对水池动力特性和地震响应有很大影响[9-10]。在设计时若不考虑这种液固耦合相互作用，直接计算水池动力特性和结构反应，可能会得到过低的计算结果，对水池的抗震性能做出错误估计，在结构设计上存在隐患，致使在地震时可能会造成严重破坏和损失，甚至会引发次生灾害[11-13]。

由于土压力的存在，对结构的受力形式也有很大的影响。SSI对结构的动力特性以及地震响应有着很大的影响[14]。所以深入系统的研究不同条件下混凝土水池在地震下的受力特征，一方面可以保证混凝土水池的结构安全，另一方面对混凝土水池的设计也具有十分重要的参考意义。

1 模型建立

1.1 FSI作用的模拟

建立水池模型时采用以下假定：液体的密度不随时间和空间变化；水池中的液体是无旋、不可压缩和不可传热的；不考虑液体的净流速，但考虑液体与池壁之间动力响应的相互作用；结构受水平方向单向的地震激励。[15-16]

为了准确的实现液体和结构之间相互作用行为的模拟，必须建立正确的液体与结构池壁接触界面处的边界条件[17-18]。在建立FSI的边界条件时，文中液体单元和结构单元分别建模，不共用节点，而是在相同坐标处分别建立液体单元节点和结构单元节点。假定水池底部为固定端，即节点所有自由度均被约束。液体与池壁接触边界处，对液体单元节点和结构单元节点耦合其法向自由度，使其在法线方向具有相同的运动，在切线方向可产生相对运动[19-20]。即液体与结构在池壁平面内可以产生相对位移，平面外相对位移为零。液体的暴露部分为自由液面。

为实现耦合界面处2种单元能准确耦合，应保证在耦合界面处液体单元与结构单元具有坐标相同的节点，即耦合界面处的液体单元节点和结构单元节点是一一对应的。这就需要在建模的过程中，耦合界面处的液体单元的面单元和结构单元的面单元完全重合且两者具有相同的网格划分尺寸。

在建立有限元模型的时候，由于水池池壁相对池壁的平面尺寸较薄，水池池壁可视为薄板，采用Shell 181单元实现模拟[21]。该单元是三维四节点单元，每个节点都具有3个平动自由度和3个转动自由度，该单元适合分析薄板和中等厚度的板壳结构，不但具有分析板壳结构与薄膜力学行为的功能，也可考虑板壳结构的剪切变形，该单元能较好的模拟水池结构的地震响应。

液体采用Fluid 80单元模拟，在三维结构实体单元Solid 45的基础上改进得到的一种三维容器液体单元，该液体单元是三维8节点单元，每个节点都只有3个方向的平动自由度。该单元是基于Housner模型简化的三维液体单元。Housner模型将液体单元简化成弹簧——质点体系，假定体系在激励荷载下做线性响应，用线性的方法研究液体的响应行为。该单元适用于容器液体、无净流速的液体的模型分析，以及有关静水压力的计算、液固耦合的计算和加速度效应等。该单元不允许退化为零体积，也不允许扭转。

1.2 SSI作用的模拟

在地震作用下，池壁前后剧烈晃动产生较大位移，时而被土体推动，时而挤压土体，土体对池壁的作用就类似于水平弹簧，侧向土体对池壁就像弹性支承。随着地震作用的变大，土体也表现出一种非线性行为[22-23]。

当池壁挤压土体时，土体所提供的土压力不能超过最大被动土压力Pp当土压力达到Pp之后，即便水池池壁位移继续增大，土体所提供的土压力也不会增大，而是继续保持为Pp；当土体推动池壁时，土体所提供的土压力不能超过最大主动土压力Pa。土压力达到Pa之后，即便水池池壁位移继续增大，土体所提供的土压力也不会增大，而是保持在Pa不变。

对于某些类型的土，特别是粘土，当结构往复晃动的时候，土体和结构可能会产生脱离或者不紧密接触的现象。这时，土体提供的土压力为零[24]。文中中假定土体是无粘性的，且不会产生裂缝。对于砂土和粘性土，我们采用Briaud和Kim推荐使用一种静态的p-y曲线来进行挡土墙设计。土压力和池壁位移关系如图1所示。

图1 土压力——池壁位移曲线Fig.1 Curve of the soil pressure-deflection of the wall

为便于在建模中实现该曲线，可将该曲线近似等效为图2中2部分组合。

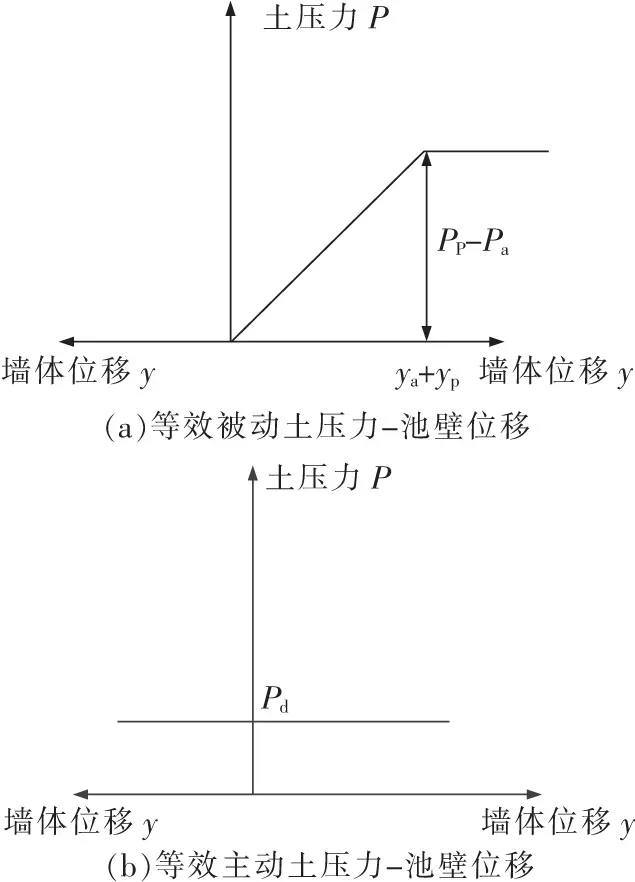
图2 等效土压力——池壁位移曲线Fig.2 Approximate representation of the soil pressure-deflection of the wall

从图2中可以看出，土体作用在池壁上的土压力可以分成2部分，第1部分随水池池壁位移变化而变化，第2部分则不随水池池壁位移变化而变化。

在建模的过程中，以节点集中力的形式来实现对面荷载的模拟。需将每个节点附近区域内的分布力等效为集中力，然后作用在节点上[25]。

土体作用在池壁上的土压力依据图2可以用水平非线性弹簧以及作用在池壁上的分布力分别来模拟。第1部分在建模中，采用Combine 39单元模拟水平非线性弹簧。因土压力——位移曲线落在第1象限，因此可以设置关键字KEYOPT(2)=1使该单元只能受拉。在每个网格划分的接点处都布置一个弹簧单元，每个弹簧单元的力——位移曲线都采用其所在深度的计算值。近似把该节点附近区域的土压力视为该处的弹簧单元集中作用在池壁上。在池壁上直接施加梯度荷载来模拟第2部分的土压力。

对于砂土，其最大主动土压力Pa、最大被动土压力Pp，以及对应的池壁变形ya和yp，将土体参数代入公式，即可得出对应土体对应的p-y曲线。

模拟第1部分的土压力时，可在每个网格划分的节点处都布置一个弹簧单元，近似把该节点附近区域该部分的土压力视为集中力，通过该处的弹簧单元集中作用在水池池壁上。

在池壁上直接施加梯度荷载来模拟第2部分土压力。通过计算，可以得出每个节点所承担的该部分的土压力。

选用2种不同性质的土体进行研究。其中坚硬土对应较硬的土体，软弱土对应较柔的土体(表1)。

表1 土体参数

图3为无水时的水池结构有限元模型。为方便下文叙述，现将4片池壁编号：y=0处池壁为池壁A；x=l处池壁为池壁B；y=w处池壁为池壁C；x=0处池壁为池壁D。如图4所示。

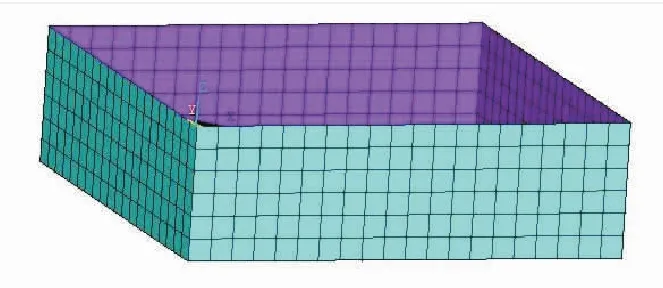
图3 无水时的水池结构有限元模型Fig.3 Finite element model of pool structure without water

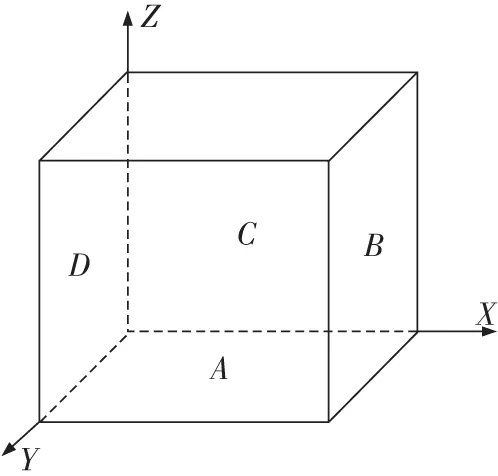
图4 池壁编号示意图Fig.4 Indication of the pool wall number

2 水池结构模态分析

在结构动力学中，系统的固有振动特性是由模态来描述的。在地震作用下结构的地震响应是表示结构体系自身特性的各阶振型的组合。因此要分析结构的地震响应，必须先对结构进行模态分析[26]。

由于文中使用的液体单元是FLUID 80单元，选用缩减法进行模态分析。因此对于研究水池结构的动力特性，选取主自由度是非常重要的一个步骤[27]。缩减质量矩阵以及最后结果的精度取决于所选取的主自由度的数目以及位置。由于所采用的模型均只受到水平方向的地震波作用，因此选择主自由度的位置在液面处的Z方向和池壁和液体相接处的法线方向。另外由于使用ANSYS在进行模态分析时会忽略材料的非线性，所以只考虑材料的初始切线模量[28]。

由于只有系统的前几阶振型对结构的动力响应的贡献最大，所以不必求出结构所有的固有频率及其所对应的振型，因此只需要求解出足够多的前几阶模态即可，这将使得求解计算量大大减少。对模型进行模态分析，采用之前所述方法分别依据表2不同工况建立了4个模型：其中，水池尺寸均为30 m×30 m×9 m。得到不同工况下结构的固有频率。

表2 不同工况下结构的固有频率

从表2中可以看出，满水工况下的水池结构固有频率比无水工况下的固有频率小。这是因为由于FSI作用的存在，液体单元的存在相当于对水池结构施加了一个附加质量，因此导致水池结构固有频率的下降。

同时，坚硬土对应的结构固有频率比软弱土对应的结构固有频率较大。因为坚硬土土质较硬，对结构的约束作用较为明显，故其所对应的结构固有频率较大。

3 水池结构地震响应

为了进一步研究考虑FSI作用和SSI作用的钢筋混凝土水池结构在地震作用下的动力响应规律，对所建立的水池结构模型施加地震波，分析其动力响应。选取El-Centro加速度时程为输入的地震波，地震波的输入方向为模型的x向，并将加速度时程的峰值调至4.0 m/s2。

3.1 池壁厚度

为研究池壁厚度对水池结构动力响应的影响，建立5组不同池壁厚度的水池结构有限元模型。各模型的尺寸均为30 m×30 m×9 m(x×y×z向)。各模型的池壁厚度分别为：0.3，0.4，0.5，0.6，0.7 m。所选取的地震波为EL-Centro加速度时程，地震波的输入方向为模型的x向，并将加速度时程的峰值调至4.0 m/s2。

底部环向等效应力峰值，指的是在水池结构的底面，从坐标x=0,y=0开始，逆时针旋转，记录每个节点在时程中的等效应力峰值以及其环向坐标。各个模型的底部环向等效应力峰值图5所示。

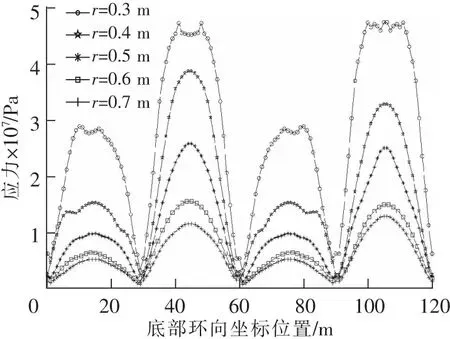
图5 不同壁厚时底部环向等效应力峰值Fig.5 Peak equivalent stress of structure bottom with different thickness

x方向位移峰值，选取B面中部一系列节点，从水池底面到最高点处，记录每个节点在时程中的沿x方向的位移峰值以及其坐标。各个模型的B面内x方向位移峰值如图6所示。

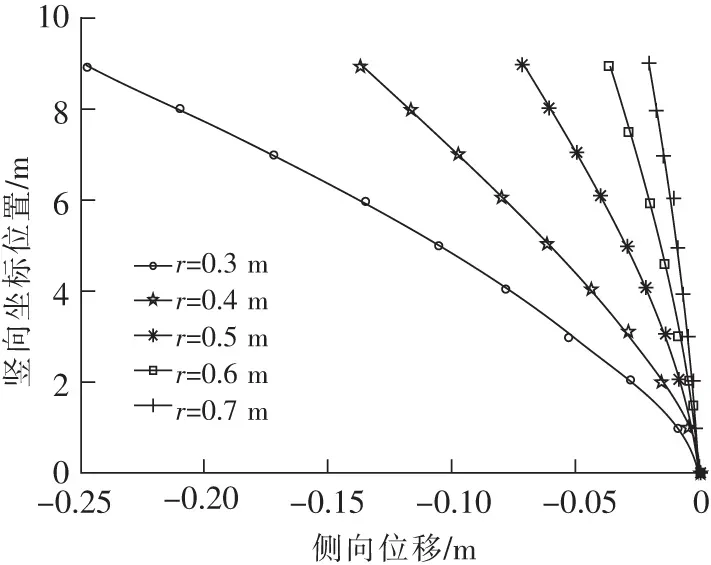
图6 不同壁厚时x方向位移峰值Fig.6 Peak delta of structure with different thickness in the direction of axis x

通过计算，可以发现。各个侧面底部的等效应力峰值整体上表现出一种对称性，一般在池壁两端较小，在中部达到最大值。各组模型的等效应力峰值均在B、D面中部达到最大，4个角点处时程内应力峰值最小。当池壁厚度较小时，应力峰值在靠近中部的位置达到最大，然后在中部有小幅降低，但是整体上还是符合中部最大、两端最小的规律，并满足对称性。从水池底面到最高点，节点的位移峰值是逐渐增大的，在最高点处达到最大。

随着水池池壁厚度的增大，水池池壁的应力及位移逐渐减小。一开始减小幅度比较大，但是当水池池壁增加到一定程度时，减小幅度开始趋于缓慢甚至停滞。实际工程中，应综合考虑应力及位移随壁厚的变化规律，选择合适的池壁厚度，使得应力和位移不至于过大，同时造价相对经济。

3.2 平面尺寸

为研究水池结构的不同尺寸对水池结构动力响应的影响，建立有不同尺寸的水池结构有限元模型，并分析对比其在地震作用下的动力响应。地震波为EL-Centro输入方向为x向，将加速度时程曲线峰值调至4.0 m/s2。

为分别对比不同的长、宽对水池结构的影响，分别改变水池在长、宽2个方向的尺寸，即平行地震波输入方向(x向)及垂直地震波输入方向(y向)。

3.2.1 长度l对水池结构的影响

所建立模型的长、宽、高，分别为18 m×30 m×9 m，24 m×30 m×9 m，30 m×30 m×9 m，36 m×30 m×9 m，42 m×30 m×9 m。

通过模拟计算，可以发现。随着l逐渐增大，A面的底部应力峰值最大值与B面的底部应力峰值最大值的比值增大并逐渐稳定，其值依次为0.184，0.299，0.315，0.431，0.440。A，C面的底部应力峰值随着l增大而增大。如图7所示。

图7 不同长度l时底部环向应力峰值Fig.7 Peak equivalent stress of structure bottom with different length

对于B面内x方向位移峰值而言，可以看出，随着l的增大，其位移峰值基本不变。如图8所示。

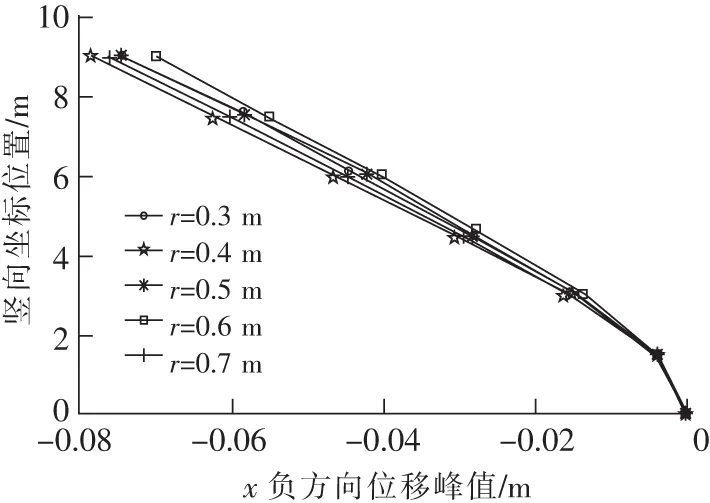
图8 不同长度l时x方9位移峰值Fig.8 Peak delta of structure with different length in the direction of axis x

3.2.2 宽度(平行y向)对水池结构的影响

建立模型的长、宽、高，分别为30 m×18 m×18 m,30 m×24 m×9 m,30 m×30 m×9 m,30 m×36 m×18 m,30 m×42 m×9 m这5种尺寸。

通过模拟计算得出，随着w逐渐增大，A，C面的底部应力峰值变化不大，B，D面的底部应力峰值逐渐增大。B面与A面的应力峰值的比值也随着w的增大而逐渐增大且逐渐稳定，其值依次为1.212，2.138，3.171，3.21，3.365，如图9所示。

图9 不同宽度w时底部环向应力峰值Fig.9 Peak equivalent stress of structure bottom with different width

从图10各个模型的B面内x方向位移峰值可以看出，随着w的增大，其数值均有明显增大，呈现正相关现象。

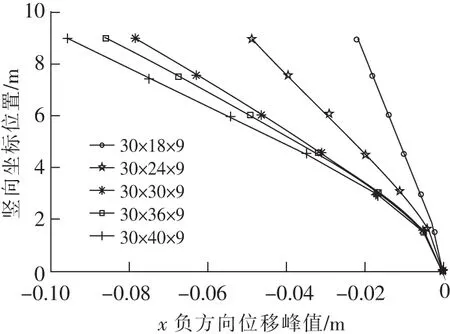
图10 不同宽度w时x方向位移峰值Fig.10 Peak delta of structure with different width in the direction of axis x

结合l,w2个变量的变化，可以看出。当l,w其中一个变量不变，另外一个变化时，随着l/w逐渐减小，A，C面的底部应力峰值与B，D面的底部应力峰值的比值减小，并逐渐趋于稳定。同时，该比值对w的变化更敏感。与地震波输入方向(文中是x方向)相垂直的池壁平面(即B，D面)的尺寸增大时，位移峰值也随之有明显增大。而另一方向尺寸的变化对位移峰值没有明显影响。

3.3 不同土质

为研究不同土质对水池结构动力响应的影响，建立不同侧向土的水池结构有限元模型，并分析对比其在不同地震波下的动力响应。所选择的地震波为El地震波、VICT地震波、人工波。地震波输入方向为x向，将加速度时程曲线峰值调至4.0 m/s2。

3.3.1 El地震波作用时结构动力响应

坚硬土所对应水池结构模型各个侧面底部的等效应力峰值均表现出对称性，并在中部达到最大值。在B，D面中部达到最大，4个角点处时程内等效应力峰值最小，如图11所示。

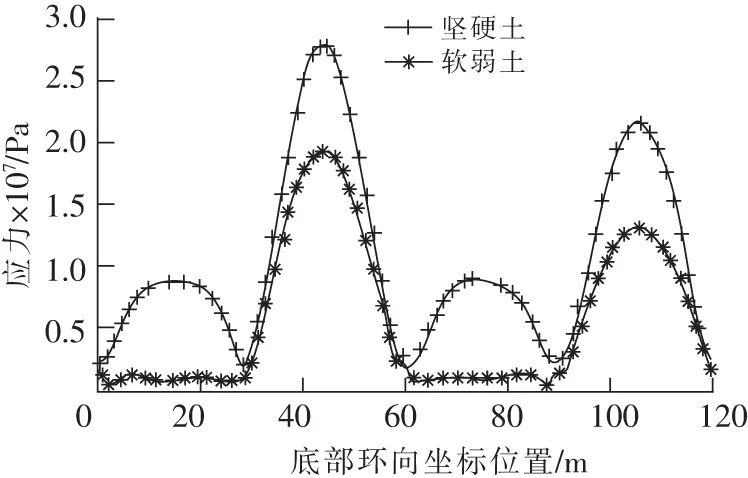
图11 El地震波时底部环向应力峰值Fig.11 Peak equivalent stress of structure bottom

从水池底面到最高点，每个模型的节点位移峰值整体上都是逐渐增大的，在最高点处达到最大。同时坚硬土所对应模型的池壁时程位移峰值与软弱土所对应模型的池壁时程位移峰值相比较大。也就是说土体主动推动水池池壁时，坚硬土造成的位移较大，软弱土造成的位移较小，如图12所示。

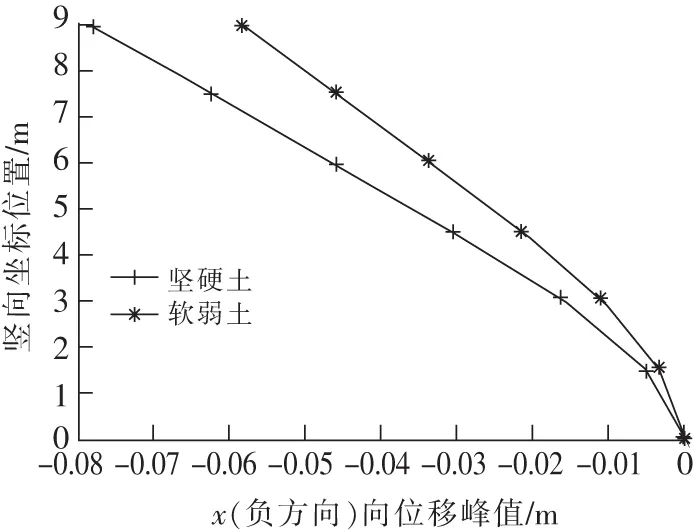
图12 El地震波时x方向位移峰值Fig.12 Peak delta of structure in the direction of axis x

3.3.2 VICT地震波作用时结构动力响应

B，D面底部等效应力峰值分布表现出很明显的对称性，在中部达到最大，两端应力较小。同时A，C面底部等效应力与B，D面相比小得多，如图13所示。

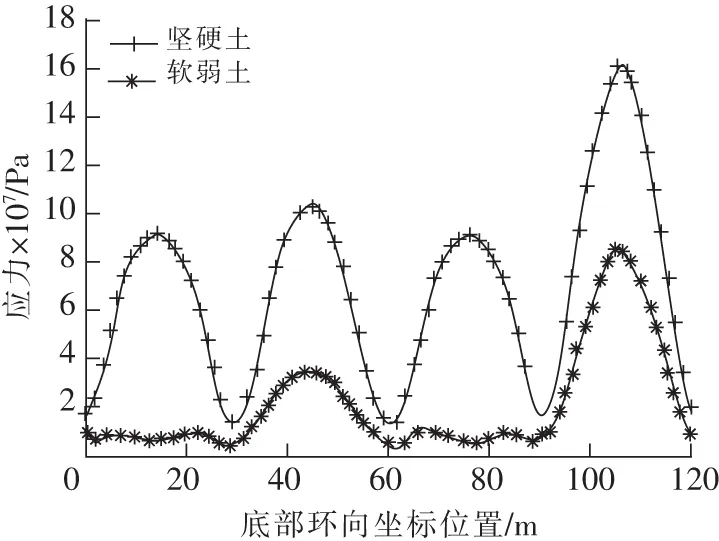
图13 VICT地震波时底部环向应力峰值Fig.13 Peak equivalent stress of structure bottom

图14是各个模型的B面内x方向位移峰值。此时水池池壁受到土体的主动推动，承受土体的主动压力。

图14 VICT地震波时x方向位移峰值Fig.14 Peak delta of structure in the direction of axis x

3.3.3 人工波作用时结构动力响应

图15为地震作用下的各模型底部环向等效应力峰值，体现了坚硬土所对应模型的底部环向等效应力峰值与软弱土所对应模型的等效应力峰值相比较大。特别是A，C面，坚硬土对应模型的等效应力峰值比软弱土对应模型的等效应力峰值大得多。

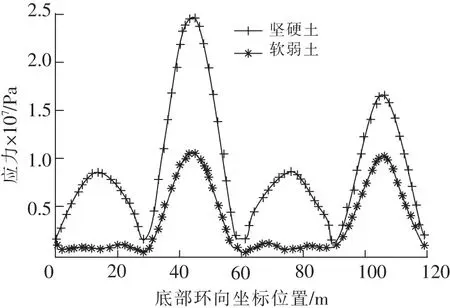
图15 人工波时底部环向应力峰值Fig.15 Peak equivalent stress of structure bottom

图16是各个模型的B面内x方向位移峰值，人工地震波所对应的数据图表所表现的规律和El-Centro地震波所对应图表所表现的规律一致。

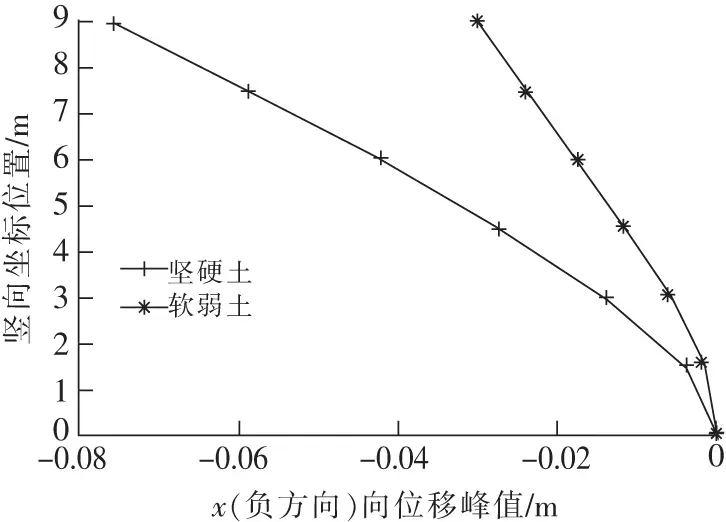
图16 人工波时x方向位移峰值Fig.16 Peak delta of structure in the direction of axis x

软弱土所对应结构，A，C面底部等效应力分布不均匀，曲线相对平缓，没有呈现出对称性，其最大值也并未出现在中部。而其B，D面底部等效应力分布则表现出很明显的对称性，最大值出现在中部，两端应力较小。同时坚硬土所对应结构的底部环向等效应力峰值较大，特别是B，D面。

同时，当土体主动推动池壁时，坚硬土所对应模型的时程位移峰值与软弱土所对应模型的位移峰值相比较大。

3.4 蓄水深度

为研究充水深度对水池结构动力响应的影响，建立5组不同蓄水深度的水池结构模型。各模型的尺寸均为l=30 m，y=30 m，z=9 m，池壁厚度均为0.6 m。各模型的充水深度分别为：0(即无水情况)、h/3,h/2,2h/3,h(即满水情况)。

单条曲线即某一充水深度下的模型对应的底部环向应力峰值都服从相似的规律。各个侧面底部的等效应力峰值表现出对称性，并在中部达到最大值，4个角点处时程内等效应力峰值最小。各组模型的等效应力峰值最大值均出现在B，D面中部(图17)。

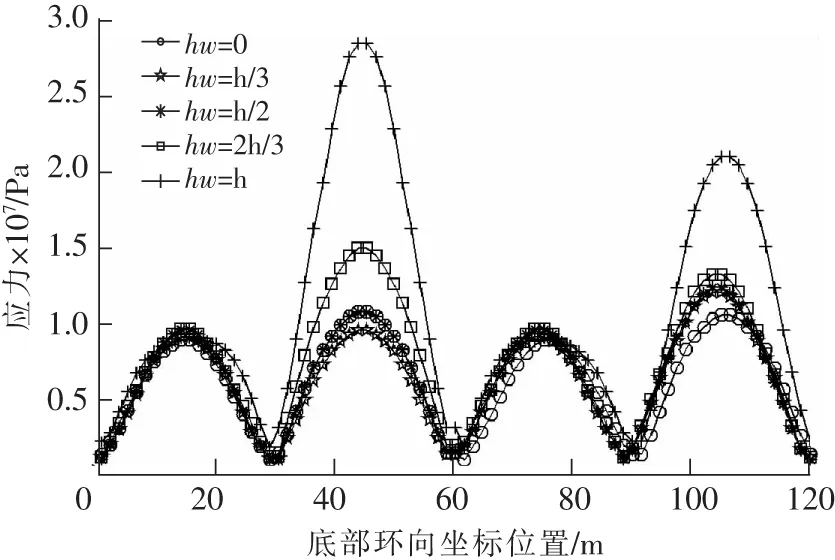
图17 不同充水深度时底部环向应力峰值Fig.17 Peak equivalent stress of structure bottom with different depth

图18是各个模型的B面内x方向位移峰值。可以看出，每条模型的位移峰值曲线对应的位移峰值都随节点坐标的增大而增大，并且每条曲线依旧表现为弯曲型。明显可以看到，随着充水深度的增加，各节点位移峰值整体逐渐变大。当充水深度从0(即无水)增加到h/2时，位移峰值基本无变化。当充水深度超过为h/2时，位移峰值有明显增大。

图18 不同充水深度时x方向位移峰值Fig.18 Peak delta of structure with different depth in the direction of axis x

通过计算，可以看出，随着充水深度的增大，水池池壁的等效应力峰值及位移峰值逐渐增大。一开始增大幅度比较小，但是当充水深度超过h/2时，等效应力峰值及位移峰值随着充水深度的增加开始显著增大，直至充水深度达到(即满水情况)，等效应力峰值及位移峰值达到最大，且增大幅度较大。同时，A，C面的等效应力峰值随充水深度增大只有略微增大，其增大幅度并不明显，而B，D面等效应力峰值随充水深度增加而有明显的增幅。