钢桁架结构平推过程稳定性能研究

张心纯，陆泽磊，周 历，任文辉，马彦阳

(1.中铁建陕西高速公路有限公司，陕西 西安 710064；2.长安大学 公路学院，陕西 西安 710064)

0 引 言

钢桁架广泛用于组合结构工程建造中，例如煤矿运输专线、大空间结构等。钢桁架-混凝土组合结构是将钢桁架与混凝土桥面板通过剪力钉连接形成整体结构，能够充分利用钢桁架的空间稳定性能和混凝土的高品质抗压性能，使其共同受力，变形协调，实现了优质组合，具有自重轻、跨越能力强、施工速度快、施工质量高等优点[1-2]。钢桁架的应用不仅减少用钢量，提升经济效益，更积极响应国家结构工程建设绿色发展的时代号召，在工程结构产业转型升级中具有较强的竞争力。

工程结构平推施工体系与施工工艺的不断完善与创新，推动了平推施工建造技术的应用。对于大跨度钢桁架结构体系，轻盈纤细的特点使得结构稳定问题成为平推施工过程中无法忽略的重要问题。结构失稳破坏具有突发性、破坏性大等特点，常造成桥梁结构垮塌等严重的安全事故，带来重大的生命财产损失和恶劣的社会影响。

目前，有许多学者对结构的稳定性能及失稳破坏机理进行研究。YU等以新黄河大桥为案例对简支钢桁梁桥的受力性能进行了研究，对轨道-桥梁相互作用引起的地震反应进行了分析[3]。赵曼等建立了128 m跨径的铁路应急钢桁梁非线性数值模型，系统分析不同荷载组合与非线性因素对结构稳定性能的影响，研究不同损伤状态下的极限荷载[4-5]。施洲等基于钢桁梁柔性拱桥有限元模型，考虑几何和材料双重非线性因素的影响，探究桥梁结构的稳定性能，系统分析钢桁梁柔性拱桥的极限承载力[6-7]。夏正春等对钢桁梁在恒载和活载作用下的稳定性能进行研究，指出加载方式对结构的稳定性能影响较大，隔跨布置活载对结构受力最不利[8]。赵雷等基于静力试验和数值模拟，探究初始几何缺陷对桁架稳定性能的影响[9]。邓海等基于车桥耦合振动理论，结合荷载试验模拟分析钢桁架在车辆荷载作用下杆件的轴力时程曲线[10]。张明等考虑多种关键因素影响确定桁架结构的最不利杆件，提出结构弹塑性屈曲承载力的计算方法[11]。ZHANG等通过风洞试验和有限元模拟，研究了大跨径板桁组合梁的颤振稳定性[12]。

在工程结构平推施工技术方面，赵人达等总结国内外桥梁顶推施工技术的发展概况，对顶推施工中导梁参数、施工控制等关键技术进行分析，探讨未来发展趋势[13]。CHACN等对钢桥顶推施工过程进行试验研究，并通过数值模拟对比分析结构的力学响应[14]。梁崇双、王盛铭等分别提出不同钢桁-混凝土组合梁施工及控制方案，探讨顶推系统的设计方案[15-16]。DING等总结某连续钢桁梁桥的悬索加劲弦杆顶推施工技术，并采用数值分析进行施工控制[17]。冀伟等研究在顶推施工过程在主梁内力的变化规律，提出导梁参数优化计算方法[18]。王金良等深入探究多跨钢桁梁顶推施工中的偏移问题，通过数值仿真计算揭示轴线偏移对钢桁梁杆件内力的影响规律[19]。时晓晔等计算分析钢箱梁顶推施工过程中导梁屈曲变形特性，探究不同加固方案对导梁稳定性能的影响程度[20]。闫纾梅等对某钢桁梁斜拉桥在施工最大单悬臂、双悬臂及成桥等关键阶段中的稳定性能进行研究，指出非线性因素对结构稳定性能影响明显[21]。

文中选取某三跨钢桁架-混凝土组合结构并建立精细化数值模型，针对钢桁架结构平推施工过程的稳定问题进行深入研究，探究了导梁长度对结构受力与稳定性能的影响，提出了导跨比的合理范围，对钢桁架-混凝土组合结构的设计与施工提供了理论参考。

1 工程背景

选取煤矿运输专线上某三跨钢桁架-混凝土组合结构为研究对象，跨径布置为3 m×80 m，单幅桥面宽12.5 m，双幅桥面宽26 m，设计荷载等级公路-Ⅰ级。钢桁架高度为8.3 m，其中桁高为7.8 m，混凝土桥面板板厚为0.4 m。钢桁架一般构造图如图1所示。钢桁架由箱型弦杆、箱型腹杆和工字型平联组成，采用Q345qDNH高强度耐候钢，在现场先焊接拼接后进行平推施工。钢主桁的两榀桁架之间通过工字型平联进行横向加强，在支点处截面采用斜向支撑加强横向联系，桁架间标准间距为6.7 m，各杆件关键截面构造参数见表1。桥面板采用预制C55高强度混凝土和1860级低松弛钢绞线，行车道板宽12.5 m，承托处板厚0.4 m，悬臂处板厚0.24 m，钢桁架之间处板厚0.3 m，通过与预留在钢梁上翼缘的集束式焊钉联结形成整体受力结构。

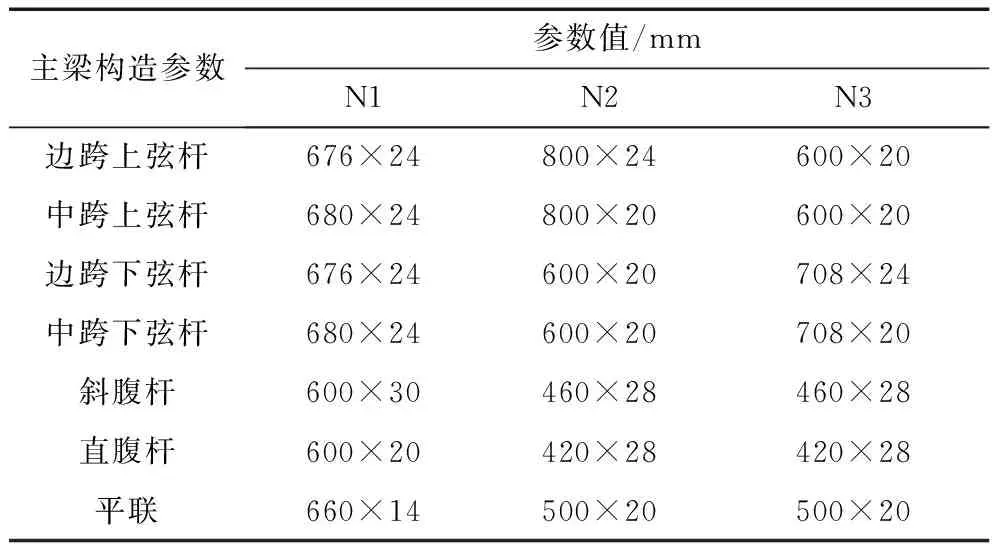
表1 杆件关键截面参数

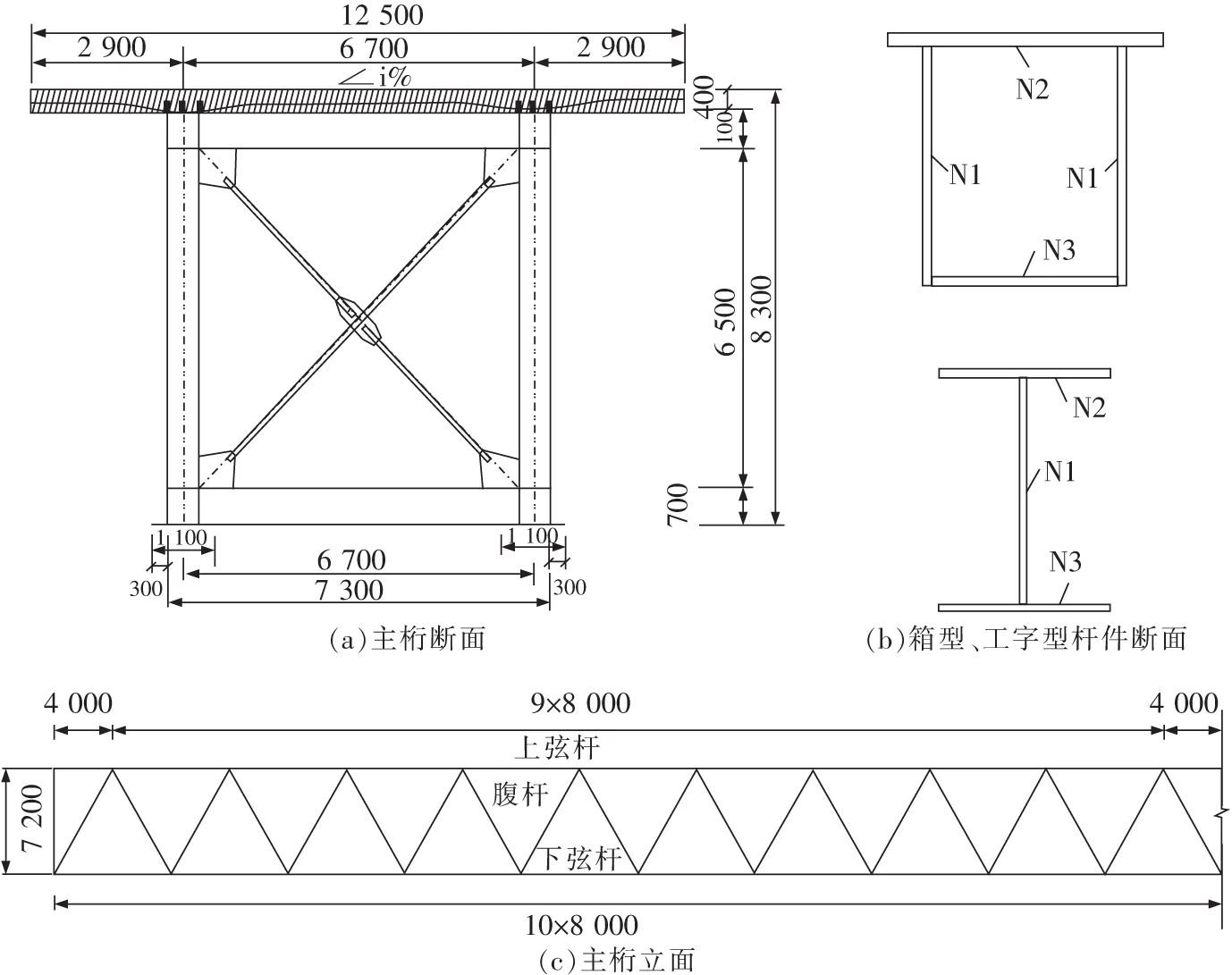
图1 钢桁架一般构造图Fig.1 General layout of steel-truss

2 模型建立

为研究钢桁架结构平推过程的稳定性能，选取与导梁连接的部分钢桁架梁段作为研究对象，通过空间有限元软件ANSYS建立钢桁架模型，对端部支点处桁杆进行分析，钢桁架-混凝土组合结构模型如图2所示[22-27]。钢桁架梁段模型通过杆件组装的方式建立，钢桁采用BEAM 188单元模拟，混凝土桥面板采用SOLID 65单元模拟，采用COMBIN 39非线性弹簧单元模拟杆件连接处的转动刚度变化，在杆件之间建立传力路径使之共同受力。在模型建立时，不考虑桥面板与钢桁架之间的剪力钉滑移效应，在桥面板与钢桁架弦杆之间采用共节点连接，并忽略实际拼接过程中造成的杆件初始变位与焊接初始缺陷。

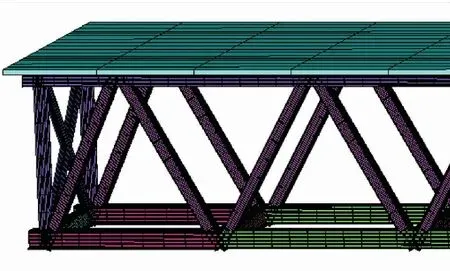
图2 钢桁架-混凝土组合结构模型Fig.2 Model of steel truss-concrete composite structure

3 平推过程梁段屈曲分析

在钢桁架平推施工时，钢桁各节段在聚四氟乙烯板和不锈钢板滑道上现场拼接，采用步履式平推设备多点同步平推，每个梁段平推结束都均进行临时约束。在平推过程中，钢桁架的结构体系随着节段前进不断变化，桁架支点与导梁连接处杆件受力复杂多变。导梁作为平推施工体系中重要的施工辅助结构，不仅大幅减小了钢桁架悬臂长度，有效降低了悬臂负弯矩峰值，对结构稳定性能的影响不容忽视。

选取导梁长度为0.6倍钢桁结构主跨径时，钢桁架最大悬臂为32 m，结合钢桁架实际平推过程，对钢桁架结构采用特征值屈曲分析，得到其作为理想弹性结构的屈曲荷载，计算了结构在平推过程中的临界荷载系数φ和临界活载系数ω，并与钢桁架成桥状态时进行对比。

临界荷载系数φ的含义为结构在荷载乘以此系数后的作用下可能出现失稳问题(屈曲)，假定结构全过程都处于线弹性工作状态，采用特征值屈曲分析的方法求出结构发生第1类失稳时的临界荷载系数。此时结构的屈曲荷载=临界荷载系数φ×(恒载+活载)。临界活载系数ω的含义为结构活载乘以此系数后的作用下可能出现失稳问题(屈曲)，采用临界活载系数ω是因为结构恒载在全寿命期间基本不发生改变，需要进一步分析活载作用下的屈曲荷载，通过不断迭代计算的方法使得临界荷载系数φ等于1，此时屈曲荷载=1.0×(恒载+临界活载系数ω×活载)。

临界荷载系数φ和临界活载系数ω计算公式见式(1)。

(1)

式中Fcr为结构屈曲荷载；FG为恒载；FQ为活载；φ为临界荷载系数；ω为临界活载系数。

图3为平推过程中最大悬臂状态与成桥状态梁段临界系数值与模态关系图，由图3可知，当钢桁架处于平推施工阶段的最大悬臂状态时，更容易出现失稳破坏，平推过程中钢桁架节段最大悬臂状态时的前三阶临界荷载系数相比成桥状态时，分别降低了13.14%，10.41%，10.85%，结构稳定性能下降明显。成桥状态下的各阶临界荷载系数波动较小，保持在4.8左右，而平推施工过程的节段最大悬臂状态的临界荷载系数随着阶数的增大呈现增加趋势。组合结构的临界活载系数随各阶模态的波动较大，平推施工过程中钢桁架节段最大悬臂状态时的前三阶临界活载系数相比成桥状态时，分别降低了10.49%，8.72%，11.19%，对结构的稳定性能影响显著。随着模态阶数的增大，降低幅度在减小，平推过程最大悬臂状态第六阶模态的临界活载系数较成桥状态减小了3.06%。

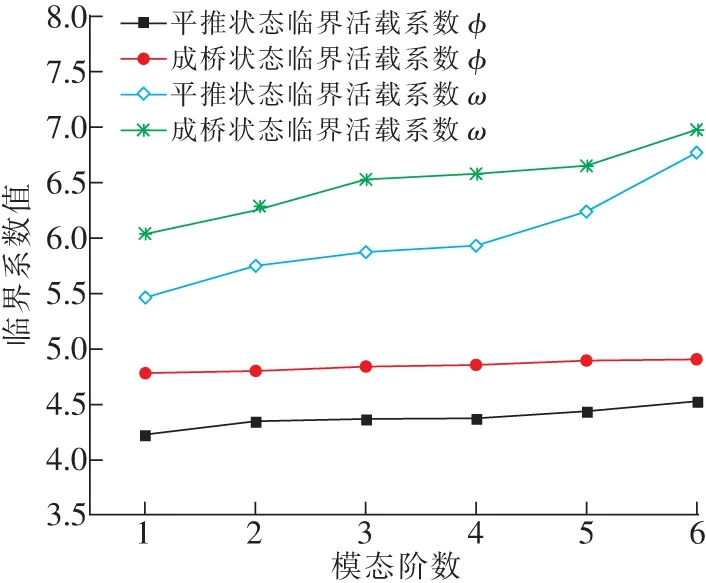
图3 临界系数值-模态阶数关系Fig.3 Relationship between critical coefficient value and modal order

4 导梁长度影响分析

在钢桁架平推施工过程中，导梁长度对钢桁架悬臂梁段的杆件内力和结构的稳定性能均有较大影响，对平推施工顺利进行起控制作用。为探究钢桁架杆件和稳定性能在导梁长度影响下的变化规律，明确导梁长度的合理范围，选取不同导梁长度与钢桁架计算跨径的比值α(导跨比)对杆件内力和梁段的稳定性能进行分析，杆件的选取如图4所示。

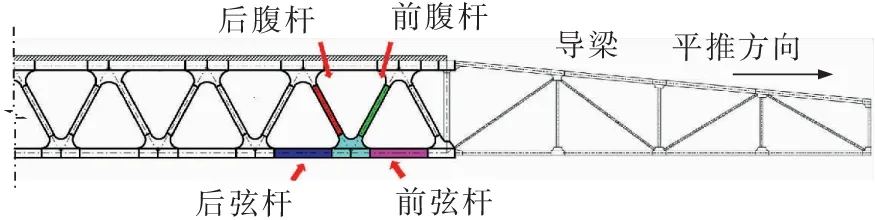
图4 平推施工示意Fig.4 Schematic diagram of incremental launching construction

4.1 导跨比对杆件内力的影响

为研究导跨比对杆件内力的影响，分别取导跨比为0.600，0.625，0.650，0.675，0.700，0.725，0.750，建立钢桁架精细化模型对平推过程最大悬臂状态进行数值分析，计算分析各导跨比下钢桁梁平推到最大悬臂阶段时端支点处梁段各弦杆、腹杆和平联内力值。图5为不同导跨比钢桁梁各杆件内力值。

图5 不同导跨比钢桁梁各杆件内力Fig.5 Internal force of steel-truss members with different launching nose-span radio

由图5可知，在钢桁架平推施工过程中，最大悬臂状态下的弦杆以受轴力为主，压力最高可达到9 528.9 kN，腹杆以受剪力为主，剪力最高可达到6 133 kN，各杆件均受到一定程度的弯矩，平联仅受极少弯矩影响。导跨比从0.600增大到0.750时，前弦杆所受轴向压力从9 528.9 kN降低到4 387.8 kN，后弦杆受轴向压力从7 509.4 kN降低到3 571 kN，降低幅度分别达到53.95%，52.44%；腹杆所受剪力从2 097.5 kN降低到1 508.7 kN，后腹杆所受剪力从6 133.1 kN降低到3 206.6 kN，降低幅度分别达到28.07%，47.72%。这是由于导跨比的增大，最大悬臂状态下导梁的长度增长，而钢桁架的长度减小，结构自重的变化导致悬臂状态的弯矩减小，杆件内力得到优化。后弦杆所受轴力相比前弦杆减小幅度超过20%，前腹杆所受剪力相比后腹杆减小幅度超过50%，说明杆件间节点刚度对内力的分配有一定影响。

前弦杆和前腹杆的弯矩数值大小和变化趋势相近，都随着导跨比的增加而减小，且导跨比越大，减小幅度越多，导跨比从0.600增大到0.750时，前弦杆所受弯矩从389.3 kN·m降低到120.9 kN·m，前腹杆受弯矩从424.7 kN·m降低到149.7 kN·m，降低幅度分别达到68.94%，64.75%。后弦杆和后腹杆的弯矩变化较大，随着导跨比的增加也呈现减小的趋势，但是在导跨比较小时，弯矩变化幅度较大，在导跨比α=0.700时出现峰值，之后弯矩呈现随着导跨比的增加而增大的趋势。

4.2 导跨比对稳定性能的影响

钢桁架作为桥梁结构的主体，在关注结构设计强度和刚度的同时，其稳定性能的重要性不容忽视，在荷载满足材料设计强度的情况下，失稳破坏是结构主要破坏模式。钢桁架稳定性能的影响因素，包括设计参数、结构尺寸、施工技术水平等。为研究平推过程中导跨比对钢桁架结构稳定性能的影响，仍选取导跨比为0.600，0.625，0.650，0.675，0.700，0.725，0.750，对钢桁架模型进行特征值屈曲分析，对比分析不同导跨比工况下钢桁架的屈曲特征值。图6为不同导跨比屈曲特征值-模态关系图。

图6 不同导跨比屈曲特征值-模态阶数关系Fig.6 Relationship between buckling eigenvalue and modal order with different launching nose-span radio

由图6可知，在同一导跨比下，结构的屈曲特征值均随模态阶数的增大而增大，且随着导跨比的增大，结构屈曲特征值有不同程度的增大趋势。从结构各阶失稳模态发现，钢桁架的破坏形态均是由杆件的局部屈曲造成的结构失稳破坏，导跨比的选取对结构屈曲破坏模式的影响较小，但对钢桁架的稳定承载能力有较大的影响。

钢桁架的屈曲特征值随着导跨比的增大而增加，当导跨比从0.600增加到0.750时，结构的一阶屈曲特征值分别提高了6.82%，20.44%，33.48%，68.08%，77.20%，87.43%，表明提高导跨比能够有效提高结构平推时的稳定性能，且当导跨比从0.675增加到0.700时，结构临界荷载系数增加幅度超过25%。结合计算结果与实际工程中导梁长度对其自身稳定性能的影响，建议在钢桁架平推施工时导跨比的取值范围在0.650～0.700之间。当导跨比因实际问题受限而小于0.600时，应采取设置临时支架等措施提高结构稳定性能。

5 结 论

1)在平推施工阶段的最大悬臂状态时，钢桁架结构的临界荷载系数和临界活载系数相比成桥状态均较小，结构稳定性能下降明显，结构更容易出现失稳破坏。随着失稳模态阶数的增加，平推施工状态的临界荷载系数和临界活载系数逐渐增大，较成桥状态的降低幅度不断减小，结构稳定性能有所提升。

2)钢桁架在平推施工的最大悬臂状态时，端支点处弦杆以受轴向压力为主，腹杆以受剪力为主，平联基本不承担轴力和剪力，仅受弯矩影响。

3)当导跨比从0.600增大到0.750时，结构自重的变化导致弦杆所受轴力和腹杆所受剪力均出现下降，前弦杆、后弦杆和前腹杆、后腹杆的降低幅度分别达到53.95%，52.44%，28.07%，47.72%。弦杆和腹杆的弯矩都随着导跨比的增加而减小，其中后弦杆和后腹杆的弯矩导跨比α=0.700时出现峰值，之后弯矩呈现增大趋势。

4)平推施工阶段不同导跨比对结构屈曲破坏模式的影响较小，但对钢桁架的稳定承载能力有较大的影响。当导跨比从0.600增加到0.750时，结构临界荷载系数提高了87.43%，且当导跨比从0.675增加到0.700时，结构稳定承载能力提升幅度较大。

5)仅通过特征值屈曲分析方法研究钢桁架结构平推过程的稳定性能，未考虑材料非线性和几何非线性对结构稳定计算的影响，下一步将采用考虑结构初始缺陷的非线性屈曲分析方法研究钢桁架结构的稳定性能。