基于3D打印技术的陶瓷工艺品包装优化设计方法
2022-08-18王书琴
苗 蕾,王书琴
(安徽文达信息工程学院 信息工程学院,合肥 230000)
陶瓷是中国十分伟大的发明,中国陶瓷源远流长,许多陶瓷工艺品受到了国内外收藏专家的青睐[1].中国陶瓷有两千多年的历史,由于陶瓷属于艺术品,在储运的过程中十分容易受到破坏,所以包装就成了陶瓷工艺品储运过程中一个十分重要的环节[2].由于大中型陶瓷艺术品的体积较大而数量较少,出于成本考虑,一般的大中型陶瓷艺术品主要采用传统的简易方法进行包装,并没有选用高档的泡沫定模工艺进行包装,而后者的运输成本十分高昂.所以,如何提升陶瓷工艺品包装效果,降低包装成本是当前研究热点的话题.
本文设计并提出基于3D打印技术的陶瓷工艺品包装优化设计方法,通过具体的仿真实验数据,全面验证了所提方法的有效性以及实用性.
1 方法
1.1 陶瓷工艺品以及包装的力学性能分析
陶瓷在冲击以及压缩加载的情况下,陶瓷材料在细观层次上的微裂纹面导致不连续的变形或者位移间断,同时还会导致气孔坍塌[3].设定εv代表破坏阵面上的状态变量,则其控制方程能够表现为以下的形式:
(1)
式中,t代表运输时间,设定CF代表破坏波传播速度,X代表微裂纹面面积,则气孔坍塌面积函数ξ(X,t)的取值范围为:
(2)
式中,C0代表材料参数,H代表Heaviside函数;τTHD代表陶瓷在冲击压缩作用下微裂纹系统所形成的剪应力阈值;τHEL代表材料在达到极限状态时的宏观剪应力[4-5],它和陶瓷材料中微裂纹系统的过渡相对应.针对脆弱性材料而言,由于静水压力和剪切应力共同影响材料的非弹性变形以及破坏响应,则陶瓷材料的脆弱性函数τ(X,t)的取值范围为:
(3)
其中,静水压力I1与剪切应力J2分别为:
I1=γij
(4)
J2=0.5γij2
(5)
式中,Φ表示破坏波参数,γij代表材料参数,参数γij的取值主要取决于材料的细观结构.针对于玻璃材料,当冲击压缩强度达到设定的范围时,则能够观察到破坏波的形成.如果设定Φ=0.5,在一维的应变条件下,以上公式能够退化为:
(6)
式中,σ1代表纵向应力;σ2代表横向应力.
针对于破坏波的传播,设定t时刻破坏波阵面位于位置A,在经过dt时间段后达到位置B.以下给出机械能守恒方程的具体表现形式:
(7)
机械能流密度能够表示为以下的形式:
W=-[σ*v]*n
(8)
机械能耗散率为:
(9)
针对脆弱性材料主要是由微裂纹拓展引发的非弹性膨胀体积应变EcV,结合相关理论,能够获取一维应变压缩,则有:
(10)
当冲击压缩下材料中的应力状态需要满足对应的破坏准则,材料内部微裂纹的成核扩展主要沿着微晶裂纹向穿晶裂纹进行过渡,其中材料的孔隙率以及静力水压之间的关系能够表示为以下的形式:
(11)
式中,nHEL代表静力水压为pHEL时所对应的材料孔隙率;Cc代表压缩系数.以下给出冲击压缩应力、破坏体积以及初始孔隙率三者之间的关系,则有:
(12)
为了准确描述一维应变条件下横向压力的变化规律,则经过破坏滤波后材料的破坏因子能够表示为以下的形式:
(13)
结合以上公式可知,材料的破坏因子会随着加载强度的增加更加趋向于极限值1,则破坏层材料的泊松比K和破坏因子p之间的关系能够表示为以下的形式:
(14)
其中,一维应变条件下的横向应力能够表示为以下的形式:
(15)
在陶瓷工艺品运输或者实验的过程中,主要包含产品以及缓冲包装材料在内的整个包装件,它是一个十分复杂的动力学系统.首先需要将包装件进行简化,通过单自由度模型,其中动力学方程能够通过公式(16)进行表示:
(16)
式中,m代表包装容器以及内装物质量;c代表缓冲包装材料的线性阻尼;l代表刚度系数.
如果令l=c,结合后退欧拉公式,则公式(16)能够表示为以下的形式:

(17)
1.2 3D打印的包装优化设计
为了进一步优化陶瓷工艺品的包装,需要结合3D打印技术对其进行包装,进一步提升打印效率.
以下给出包装件的具体动力响应过程,如图1所示.
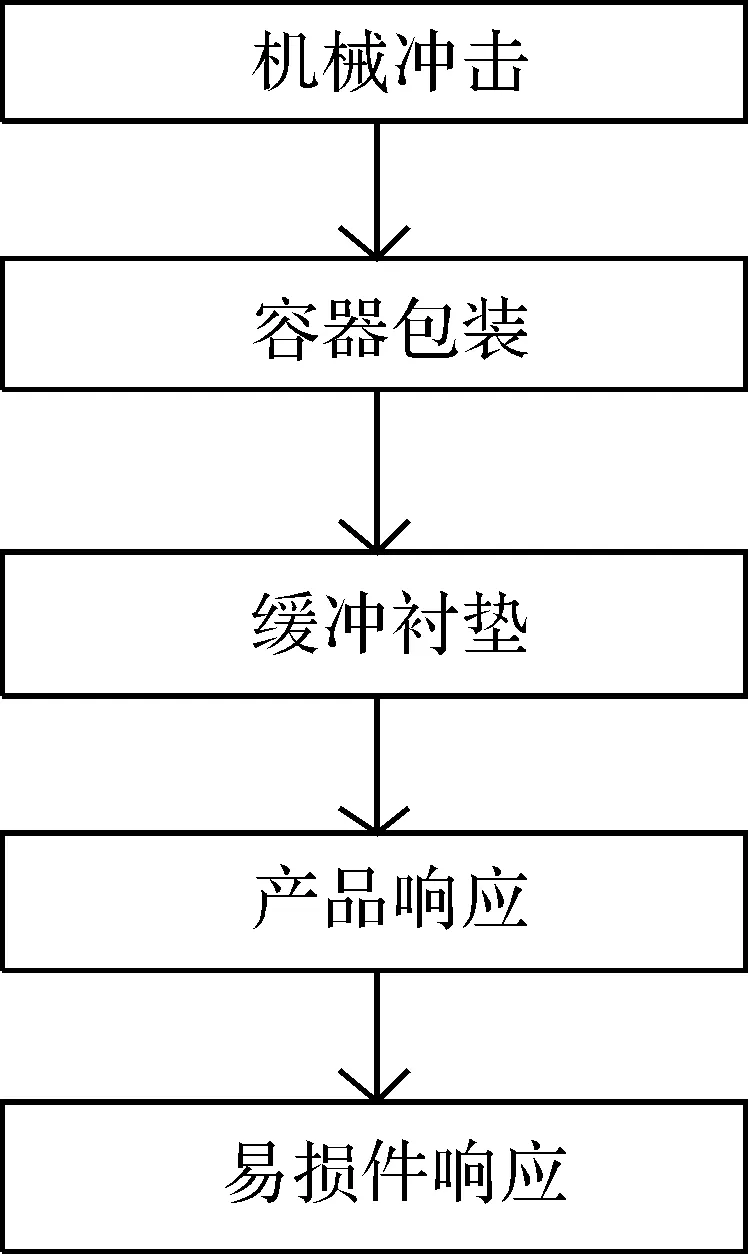
图1 包装件的具体动力响应过程
其中陶瓷工艺品的包装材料尺寸计算公式为:
(18)
(19)
式中,L代表缓冲衬垫面积;δ代表产品的重量;Sv代表产品脆值以及冲击加速度;μ代表缓冲材料最大的应力;T代表缓冲衬垫厚度.
结合以上公式,能够获取缓冲垫的厚度面积,具体的计算式如下:
(20)
(21)
在上述操作的基础上,在衬垫的基础上进行审计,需要引用一系列的试验特性曲线以及数据,它们全部都是以假定的理想姿态为前提进行设计的,但是衬垫的实际工况并不是标准姿态.在实际流通的过程中,主要包含包装件跌落姿态变化,由于受力情况不同,以下需要对基础设计尺寸进行对应的调整.其中承载面积能够通过以下公式进行计算:
(22)
式中,Ae代表承载面积;E代表产品的长度;b代表产品的宽;q代表次数,它的取值通常情况下为1.
其中静应力的计算式能够表示为以下的形式:
(23)
在上述分析的基础上,结合3D打印技术,对陶瓷工艺品包装进行优化设计.以下给出具体的操作流程图,如图2所示.

图2 陶瓷工艺品包装优化设计流程图
采用Runge-kutta方法对线性系统和非线性系统进行数值模拟,得到不同参数对关键部件的影响,其中主要包含陶瓷工艺品包装的材料选择以及结构设计.为了提升包装效率,需要在整个方法中加入3D打印技术,获取最佳可行包装设计方案.具体的计算式如下:
Fqu=L+η
(24)
综上所述,完成了基于3D打印技术的陶瓷工艺品包装优化设计.
2 仿真实验
为了验证所提基于3D打印技术的陶瓷工艺品包装优化设计方法的综合有效性,需要进行仿真实验.实验环境为:Windows XP操作系统,Matlab7.0软件,Dual Core Intel Pentium D CPU2.10GHz PC,2GB内存.
2.1 生产效率
为了验证所提方法的有效性,以下需要对比不同陶瓷工艺品包装优化设计方法的生产效率.三种方法的具体对比结果如图3所示.

图3 不同方法的生产效率
分析图3可知,随着抗压强度的不断变化,各种方法的生产效率也在不断变化.当压强增大到100 MPa时,平面设计理念的包装设计方法的生产效率为73%,不同防护材料的包装结构设计方法的生产效率为68%,3D打印的包装优化设计方法的生产效率为89%.由以上结果可知,3D打印的包装优化设计方法的抗压能力较好,生产效率较高.
2.2 生产效益
为了更进一步验证所提方法的生产效益,以下需要对比三种方法的生产效益.具体的对比结果如表1所示.

表1 所提方法的生产效益变化情况
分析表1可知,三种不同方法下生产效益不同.当陶瓷个数增加到500个时,面设计理念的设计方法的生产效益为6.97万元,不同防护材料的设计方法的生产效益为7.89万元,3D打印的设计方法的生产效益为16.87万元.可以看出本文方法的生产效益较高,同时随着产量的增加,3D打印的设计方法的生产效益与其他两种方法差距增大.说明相比传统方法,所提方法能够有效提升生产效益.
3 结束语
针对传统的陶瓷工艺品包装优化设计方法存在的一系列问题,设计并提出基于3D打印技术的陶瓷工艺品包装优化设计方法.实验结果表明,当压强增大到100 MPa时,3D打印的包装优化设计方法的生产效率为89%.当陶瓷个数增加到500个时,3D打印的设计方法的生产效益为16.87万元.现阶段所提方法虽然已经取得了十分显著的研究成果,但在节约生产成本上仍需要进一步优化,未来阶段将针对这点不足进行进一步完善.
