橡胶弹热效应的研究现状与展望

2022-08-18王玉梅

制冷学报 2022年4期

王玉梅杨萌刘斌

(天津商业大学天津市制冷技术重点实验室天津 300134)

制冷技术在我们的生活中起到至关重要的作用，如食品冷冻冷藏、空调、电子设备的冷却等。随着人们对节约能源和保护环境的重视，为满足可持续发展的理念，传统蒸气压缩式制冷面临着严峻挑战。为缓解制冷应用对环境的影响，一方面，制冷剂的替代问题亟待解决[1-3]；另一方面，基于固体材料热效应的新型制冷技术也是一种替代方案。其中，固体材料的热效应主要包括磁热效应(magnetocaloric effect, MCE)、电热效应(electrocaloric effect, ECE)、压热效应(barocaloric effect, BCE)和弹热效应(elastocaloric effect, eCE)。据统计，制冷行业消耗电力占全球总电力的比例已超过15%[4]。近年来，利用磁热和电热效应制冷的固体材料受到人们的重点关注，但磁热效应所需的磁体和MC材料主要基于稀土元素[5-6]，其生产对环境有害[7]。砷基MC材料[8]和铅基EC材料[9-10]具有高热性能，但有毒。有一些具有高热效应的材料对环境友好，但成本较高，如广泛研究的PVDF基聚合物[11-12]，因此基于磁热效应和电热效应的固态制冷技术没有投入实际应用。

弹热制冷是由应力场驱动弹热材料相变产生制冷效应的固态制冷技术[13]。根据美国能源部的报告[14]，弹热制冷技术因其潜在的高效率成为替代蒸气压缩制冷技术中最具潜力的新型制冷技术。目前研究最多的具有弹热效应的材料是形状记忆合金，可实现20 K的绝热温度变化[15]，但超过500 MPa的应力才能实现5%的应变[16]，需要的驱动装置有待开发研究，对于紧凑的制冷装置，形状记忆合金具有显著优势[8-14]。

天然橡胶(natural rubber，NR)是一种以异戊二烯为主要成分的天然高分子化合物，自补强性，具有较高的强度和抗裂纹扩展性，应变幅度为3的非结晶应变下的疲劳寿命为2 000个循环，而应变诱导结晶的应变在1.7×105个循环后仍未裂化[17-18]，但温度变化降低12%，应力减少46%[19]。天然橡胶在双向拉伸时，当应变幅度约为2时疲劳寿命可达到107次[20]。

天然橡胶也具有环境友好、可回收、成本低、无毒等优点[15]。最显著的物理性质是弹性模量非常小，仅为钢铁的1/30 000，但伸长量却是钢铁的300倍[21]。具有很好的弹性，伸长率最高可达1 000%[22]，小应力可以产生大形变，与形状记忆合金相比，驱动装置更容易实现，耐疲劳且疲劳损伤可以高温修复。因此，天然橡胶在弹热效应领域具有巨大的潜力。本文围绕橡胶的弹热效应展开分析与研究，重点对天然橡胶的弹热效应进行分析。

1 橡胶弹热效应的原理及热力学基础

1.1 橡胶弹热效应的原理

英国物理学家J.Gough[23]最早在19世纪初期发现天然橡胶具有弹热效应并提出了相关理论概念。Gough理论在50年后被J.P.Joule[24]证实，Joule当时采用的是已经存在的更具可逆性的硫化橡胶，这两个效应即目前为人所知的Gough-Joule效应。

H.M.James等[25]提出一种包括分子链间相互作用在内的块状橡胶动力学行为的严格理论。橡胶弹性被描述为热弹性，称为熵弹性[26]。当弹性材料被拉伸时，弹性分子段的两端在拉伸方向上分子链越来越有序，温度升高，熵减小。当拉伸应力释放时，随着材料向其初始无序状态恢复，温度降低，熵增加。熵弹性主要表现在交联弹性体聚合物(弹性体)、形状记忆合金和铁电材料上[27]。

1.2 橡胶弹热效应热力学

D.Guyomar等[28]通过理论分析给出了机械应力作用下天然橡胶温度微分方程的整体描述。通过建立温度变化函数的分析模型，确定一个弹热常数γ：

(1)

假设橡胶材料与环境之间的热传递是由对流和辐射产生，则天然橡胶与环境之间的温度热交换与伸长量的关系为：

(2)

由于熵变与应变和温度变化是成比例的，则天然橡胶的制冷能力表示为：

(3)

Xie Zhongjian等[29]对NR的eCE直接测量(绝热温变ΔT)和以推导出的式(4)为计算依据的间接测量方法进行对比。采用的NR初始长度为10 mm，横截面积为20 mm×100 μm。间接测量方法分为两种：1)测量不同静态温度下的应力应变特性；2)测量恒定应变下的应力与温度。方法1)得出应力非状态变量，且橡胶复杂的相变导致该方法推导出的eCE较低；方法2)推导出的eCE与直接测量的ΔT基本吻合，这也验证了推导出的麦克斯韦方程是有效的，在绝热条件不易实现时可采用第二种间接测量方法来研究NR的 eCE。

(4)

1.3 橡胶弹热制冷循环及动力学理论

理想情况下，弹热制冷最简单的循环包括4个过程，如图1所示。与理想气体卡诺循环相似：两个可逆绝热过程用来描述物质温度变化导致材料的热能变化过程；两个可逆等温过程用来描述热能变化的热传导过程。理想橡胶的制冷效率与卡诺循环制冷效率的计算方法相同，热泵和制冷循环的性能系数(coefficient of performance, COP)如式(5)和式(6)所示，具体推导过程参考文献[30]。

图1 理想的弹性体制冷循环原理[30]

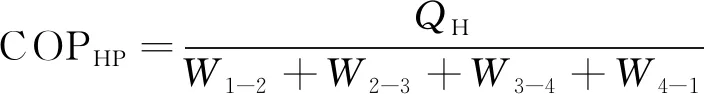
(5)

(6)

式中：QH为过程2-3所需制冷量，W;QL为过程4-1所需制冷量，W；W1-2、W2-3、W3-4、W4-1分别为各过程所需轴功率，W。

动力学理论以其最简单的形式把橡胶的弹性归因于一个长链分子系统从无应变状态过渡到应变状态时构象的变化。对于橡胶材料的高弹性本构方程，主要有两种：一种是基于连续介质力学的唯象理论，包括多用于中等变形条件的Mooney-Rivilin模型[31]、拥有更大应变适用范围的Yeoh模型[32]以及以拉伸比λ为研究基础的ogden模型[33]和Valanis-Landel模型[34]等；另一种是基于分子结构的统计理论，包括高斯链与非高斯链两种假设，其中非高斯网链模型适用于大变形阶段的模拟和预测，在小应变阶段的误差较大，为减少这种误差，很多学者也提出了混合模型[35-37]。

2 橡胶的弹热效应研究

目前，对橡胶弹热效应的研究主要围绕天然橡胶进行，只有少数学者对不同橡胶的弹热效应进行了对比。王孟[38]对天然橡胶和丁腈橡胶的拉伸-回复热效应进行了研究，采用红外热像仪记录橡胶的温度变化，观测到了弹热效应，并通过计算分析验证了内能在拉伸过程中对应力的贡献。李天颖[21]以天然橡胶、硅橡胶、顺丁橡胶、丁苯橡胶和氯磺化聚乙烯为研究对象，对不同橡胶材料的弹热效应进行研究，在 500 mm/min 的速率下对消除了 Mullins 效应的实验试件进行拉伸-回复实验，得出对橡胶弹热效应影响较大的因素分别为交联度、结晶度、弹性以及不可逆度。天然橡胶在这5种材料中的表现最佳，最具应用潜力，硅橡胶、顺丁橡胶和丁苯橡胶作为弹热制冷材料仍有较大潜力，前提是要调配好分子之间的交联度。此外，硅橡胶本身拉伸强度仅约为0.3 MPa[39]，在实际应用中需要使用补强剂来增大拉伸强度。加入芳纶纤维、碳纤维和聚酰胺纤维后可使顺丁橡胶复合材料的硬度和撕裂强度提高22.5%[40]。

乳胶橡胶属于橡胶类的热塑性合成树脂，聚合物的结构由单元组成，这些单元连接在一条普通的链中，不能独立在空间中运动，该结构导致橡胶的熵异常低，乳胶橡胶具有负热膨胀系数[41]，适用于动态下部件的粘接和不同热膨胀系数材料之间的粘接。E.V.Morozov等[42]以宽5 mm、厚0.6 mm、长7.3～44 mm的乳胶橡胶作为实验材料，研究了胶乳橡胶在周期性拉伸力作用下的弹热效应，揭示了三种不同热力学过程的循环频率，低频率(0.1～0.3 Hz)，eCE稳定且高，在应变为7时，最大温变为14 K；中频率(0.3～1 Hz), eCE有所降低；高频率(1～4 Hz)，eCE显著降低。实验结果表明，乳胶橡胶的温度变化与伸长率呈非线性关系，如图2所示。乳胶橡胶的比制冷功率与频率呈非线性关系，随着频率的增加而增加，当频率f=4 Hz时，比制冷功率达到最大值(q= 10 W/g)，如图3所示，比制冷功率定义为频率的函数：

图2 不同拉伸频率下乳胶橡胶的温度变化与伸长率的关系[42]

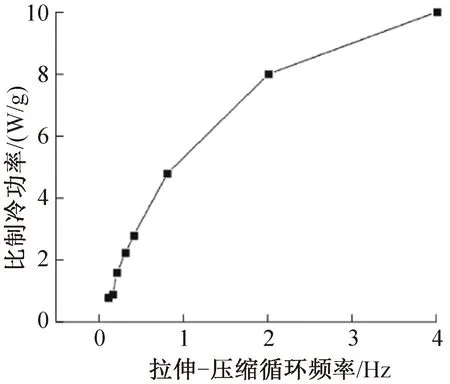
图3 应变为5时弹性体的比制冷功率与拉伸-压缩循环频率的关系[42]

q=cΔTf

(7)

Wang Run等[43]研究发现对NR纤维进行加捻-解捻过程可以产生制冷效应，利用3 cm长的NR纤维，拉伸速率和旋钮速率分别为42 cm/s和50 r/s。通过实验得到，等轴应变为3时，高捻度、螺旋和部分超螺旋纤维的NR表面平均温度变化分别为3.3、6.5、7.7 ℃，而未加捻纤维的表面平均温度波动为2.4 ℃，部分超螺旋结构的表面最大温度变化为12.9 ℃，是未加捻NR纤维的5.4倍。将7股直径为2.2 mm的NR扭在一起产生了更高的平均表面温度变化(12.2 ℃)。文中展示了一种利用扭热来冷却流动水的冷却装置，获得相同降温效果的情况下，扭热制冷的体积仅为弹热制冷的2/7，NR纤维在应变为1、中捻度密度下，获得的最大扭热比冷却量为19.4 J/g,是弹热制冷的24倍。

乳胶橡胶强自加热及之后的失效发生在较高的频率，f>1 Hz时的寿命约为1 000个循环，仅能运行5～10 min，不能满足实际应用需要的107～108个循环[34]。

橡胶的温度变化可用来研究应变诱导结晶(strain induced crystallization, SIC)的动力学，SIC的研究也可以指导橡胶弹热效应的研究。J.R.Samaca Martinez等[44]用红外热像仪在环境温度下，在循环单轴力学试验中测量天然橡胶的温度变化，结果表明聚合物链在张力下结晶，导致温度升高，并经过应力松弛试验表明，结晶热特征与结晶熔融热特征不同，橡胶的结晶过程在应力松弛过程中发生。Y.Miyamoto等[45]通过应力-应变-温度的测量，研究了硫化天然橡胶在单轴变形下的结晶和熔化。在一定的温度和应力条件下，结晶橡胶的熔化温度随名义应力近似线性增加，熔化温度随应力升高的主要原因是熔化时的收缩功，而不是熔化态变形熵的减小。在一定温度下，当名义应力高于熔化应力时，结晶速率单调增大，在一定应力下，结晶速率在温度范围内达到最大值，结晶度随交联度的增加而减小。A.N.Gent等[46]采用膨胀剂法，利用天然橡胶的体积变化研究了天然橡胶低温结晶的动力学，发现未拉伸天然橡胶的最大结晶速率发生在约-25 ℃，再进一步降低温度时，天然橡胶的结晶速率连续降低。

1925年，J.R.Katz[47]在天然橡胶中用X射线衍射法发现应变诱导结晶现象，至今一直被广泛研究。J.M.Chenal等[48]在弱硫化和高硫化天然橡胶样品拉伸过程中，进行了一系列新的原位同步X射线衍射实验。从晶粒尺寸和结晶速率两方面对实验数据进行了分析,发现天然橡胶中物理纠缠态之间的分子量是SIC的关键参数。B.Huneau[49]综述了近年来有关天然橡胶结晶相结构的研究进展。该结构具有很强的各向异性，可能与该材料异常良好的强度和疲劳性能有关。在张力收缩实验中，SIC材料可以通过同步辐射进行实时研究。这些研究的主要结果是，未填充NR的力学滞后主要是由SIC引起，更准确的说是结晶开始时拉伸比与结晶熔化时拉伸比的差异。P.A.Albouy等[50]描述了一种频闪X射线衍射机，可以研究天然橡胶中SIC的动力学方面，确定了非晶态组分的晶含量、晶态取向和段序参数。在低变形速率下的常规机械循环过程中，由于SIC，保持熔融状态链存在一个应变调节过程；在中等振幅和低于一定平均延伸率的周期循环条件下，熔炼延迟可导致结晶含量的均衡。另一方面，结晶是一个快速的过程，可达到最大循环频率对应于17 ms的拉伸时间。

S.Toki等[51]利用同步辐射X射线，研究了NR未硫化态和硫化态的应力-应变关系和SIC，温度范围为-50～75 ℃。未硫化NR在25 ℃表现出SIC与应力呈上升关系；当应变小于3.0时，硫化NR的应力与红外应力基本一致，但当应变超过3.0时，硫化NR的应力明显高于红外应力。在较高的应变下，碳化硅材料成为大的网状点，捆绑了许多链条，降低了延伸极限。碳化硅对应力的影响和有限的延伸性是不可区分的。

N.Candau等[52]利用原位广角X射线散射测量，在室温和低应变速率(10-3s-1)下，对天然橡胶的应变诱导结晶进行了表征。在加载和卸载过程中测定了三个主要方向的结晶度指数和晶粒的平均尺寸。他们认为，在涉及结晶的链中存在记忆效应，这减缓了晶体的成核过程。

Xie Zhongjian等[53]研究了预拉伸对NR弹热效应的影响。与无预拉伸变形相比，预拉伸可以跳过低弹热系数区，直接进入SIC引起的高弹热系数区。特别是当预拉伸作用于SIC之前时，弹性热系数达到最大值，当预拉伸作用于进入SIC区域时，弹性热系数再次下降。此外，当在SIC开始施加预拉伸时，应力输入是最大的。在实际应用中，因不可逆过程会导致样品整体温度升高且可能会接近韧性极限，所以要尽量避免不可逆过程。

橡胶的力学行为主要归因于SIC，因为SIC对温度敏感[45,54-55],因此，橡胶的力学行为与温度有关，会随温度的变化而变化。

在极低的应变下，拉伸的速度足够快，SIC主要发生在保持拉伸的状态。SIC链比非晶体链长，部分结晶链能够松弛剩余链并松弛应力(SIC的应力松弛效应)[19，56]。因此，当拉伸状态保持松弛应力时，即拉伸应力和收缩应力的差异，可以用于演示SIC行为。具体而言，它的温度依赖性是指SIC的温度依赖性。

郑兴邦[57]通过将天然橡胶拉伸不同的长度，研究发现天然橡胶在拉伸作用下，会发生SIC。天然橡胶在100%拉伸状态下便会产生SIC，且随着拉伸长度的增加，结晶度增大；未硫化的天然橡胶在拉伸400%时产生了新的结晶结构，结晶度为59.4%；天然橡胶在500%拉伸长度时可以看到新的晶体结构，结晶度为32.3%。J.R.Katz[47]提出未拉伸的NR也可通过冷却结晶,该现象被称为热诱导结晶(temperature induced crystallization，TIC)。

Xie Zhongjian等[58]研究了温度与应变对NR弹热效应的影响，结果表明：天然橡胶的最高弹热能力出现在约0 ℃、应变为6时，最大温变为12 K。从10 ℃至0 ℃，温变出现急剧下降，温变从12 K至4 K，但松弛应力随温度降低而增加，这与绝热温变的变化趋势相反，因为在接近0 ℃时，NR中的TIC现象显著。在低温时TIC是不可逆的，这也说明绝应力松弛是SIC和TIC共同作用的结果，并且在较低的温度下拉伸和收缩过程均会导致较高的结晶度，导致在较低温度下会有更大的应力滞后区域。

图4所示为不同应变和不同温度下的松弛应力对比。由图4可知，在不同应变下，松弛应力均随温度的降低而增加，即结晶度会随温度的降低而增加。此外，仅在较低温度(0、10 ℃)下，松弛应力从应变为5起变为饱和。这可能是因为在温度下降时SIC的早期应变所致[53]。图5所示为在不同温度和不同应变下的绝热温变ΔT对比，插图为应变为6时绝热温变ΔT随温度的变化。

图4 不同应变和温度下的松弛应力[58]

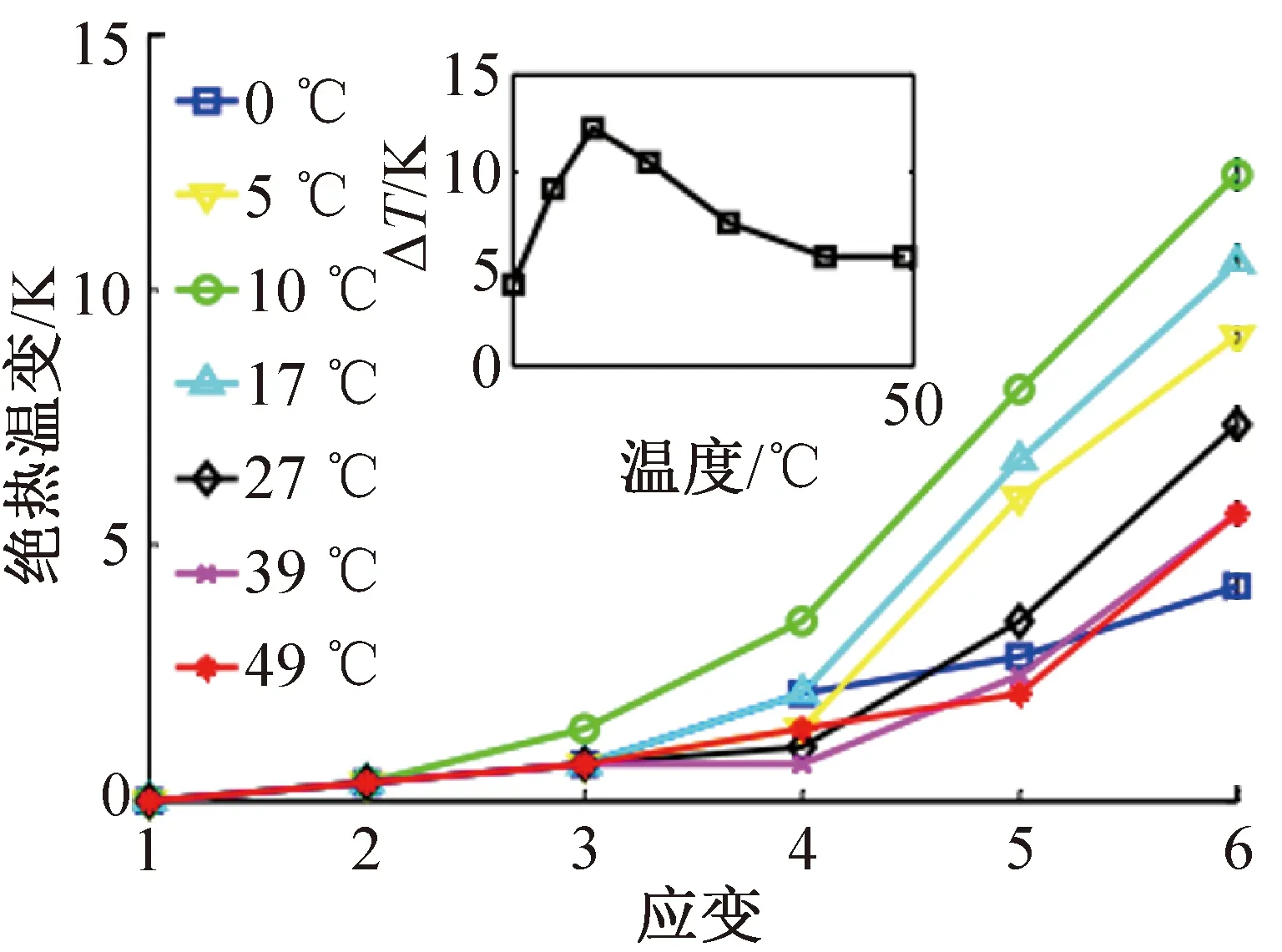
图5 不同应变和温度下的绝热温变[58]

G.Sebald等[19]研究了疲劳对NR弹热效应的影响。实验研究了不同振幅下的工程应变循环，观察到实验中天然橡胶断裂的循环次数是有限的(约800个循环)，显示出非常短的疲劳寿命。实验主要研究了应变分别为0～3、2～5、4～7三种应变振幅为3的小振幅应变状态下弹热效应的疲劳依赖性。其中，应变0～3为非晶体应变区，应变2～5和4～7为SIC应变区。实验结果表明：与SIC高应变(应变为4～7)下工作相比，在SIC工作开始时(应变为2～5)可获得更好的疲劳寿命和更小的应力退化，且在熔化开始时(应变为2～5)获得了最高的性能。

3 天然橡胶弹热效应的循环分析

早期对橡胶弹性体热力学的研究主要用于课堂教学[59]。W.B.Wiegand[60]在1925年提出了两种弹性体循环热机的设计。

1)由橡皮筋辐条的车轮组成，辐条连接到围绕偏心轴旋转的环上，当大轮子旋转时，辐条的长度会发生变化，轮辐在旋转的一个区域被加热，在另一个区域被冷却，这推动了车轮的扩张和收缩，并产生了扭矩。对该模型进行分析，曲柄的曲轴也可以围绕圆周的同一中心旋转，如图6所示，考虑两个橡胶曲柄臂，它们连接在曲柄臂的端部和轮辋上相距180°的两个位置。若轮辋半径为R，曲柄位置角为α，则橡胶可以拉伸到的最大长度为R+d，而最小长度为R-d。假设原始未拉伸长度为l0，则最大和最小拉伸比为：

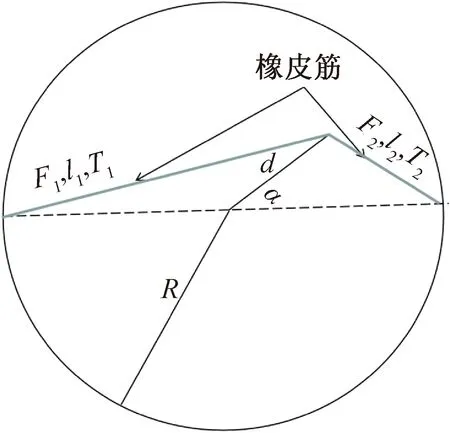
图6 带有一对元件的Wiegand发动机示意图

(8)

(9)

对于这种发动机配置，有两种简单的方法重复拉伸橡胶:(a)固定曲柄并旋转轮圈；(b)保持轮圈固定并转动曲柄。对于后一种情况，若两个橡胶曲柄臂的温度相同，则它们施加在曲柄臂上的力的大小与曲柄位置角α无关，且力总是指向曲柄。因此，这些力不会导致力矩耦合，且曲柄臂将保持在其放置的任何位置角度或等效地转动曲柄不需要扭矩。

2)另一种设计由一个由橡皮筋收缩驱动的慢周期钟摆组成，当钟摆摆动时，橡皮筋交替暴露在加热灯下或隐藏在阴影下，从而依次吸收和放出热量。

W.B.Wiegand建造并操作了这两种设计的原型，并提议使用巨大的太阳能驱动橡胶发动机来发电。这两种设计原型也为其他学者提供了灵感。

C.L.Strong[61]讨论了几种转子式发动机，其中大多数采用偏心轮设计，也有一部分采用水平轴设计，橡皮筋的收缩会打破转轮的平衡，使其发生转动。这些设计本质上受到加速度的限制。R.Farris[62]通过设计一个小型橡胶纤维发动机，证实这些发动机在使用现代弹性纤维设计时具有高功率潜力，当热源与散热器间的温差为30 ℃时，比制冷功率达到1 W/g，说明使用弹性纤维的发动机具有高功率潜力。R.E.Lyon等[63]对两种聚氨酯弹性体在不同的应变和温差下进行了热机循环实验，使用的两种弹性纤维为市售的聚结复丝纱线，实验结果表明：在小应变扰动下，弹性材料接近力学平衡时，其功率和热效率达到最佳。证实了实验规模的热机中橡胶的准理想性能的结论。J.G.Mullen等[64]提出真正的橡皮筋有一个复杂的状态方程，如果以理想化的方式来限制这些参数的范围，则可给出状态方程的近似描述。同时开发了一个发动机最大允许摩擦的标准，并指出了如何获得最小摩擦扭矩[65]。

F.Greibich等[66]基于天然橡胶的柔软、廉价、可生物降解等特点，设计了橡胶基全软热泵，该热泵将天然橡胶的不稳定性与应变诱导结晶结合，实现了最大循环频率对于拉伸时间低于100 ms的精准绝热循环，热泵的制冷功率为20.9 W/g，热流密度为256 mW/cm2，COP为4.7，橡胶膜的完全绝热温度变化超过23 K。Zhang Shixian等[67]研究证明具有均匀分子链长的聚合物弹性体通过可逆的构象变化表现出巨大的弹性热效应，因此针对橡胶的高应变特性设计了一种旋转冷却装置，有效释放了聚合物弹性体的冷却能量。D.W.Gerlach等[30]提出以橡胶为弹热工质的热泵或制冷系统运行时，分为4个路径：绝热拉伸、等温拉伸、绝热收缩、等温收缩。搭建了一个概念原型机，如图7所示，在呈 180°角的曲轴两端，连上几根长橡皮筋，橡胶的另一端接在固定杆上。运行过程中当曲轴旋转时，这些橡皮筋交替拉伸-回缩，再分别与两个铝板接触进行等温拉伸放热和等温回缩吸热。橡皮筋在运行过程中的最短长度是当其完全松弛时的长度(即拉伸比为 1)，最长距离为拉伸比 2～3 时。两个铝板由铰链连接，平衡锤及上部铝板的重量压在底部铝板上来保持板与橡胶的连续接触。橡皮筋通过曲轴从一个铝板上换到另一个铝板的短暂过程可视为理想循环中的绝热过程，这些铝板用泡沫隔热并连接热电偶用于测温。

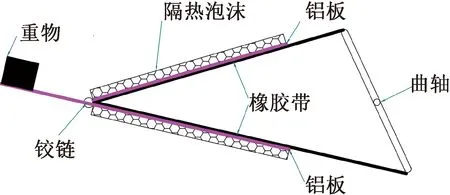
图7 弹热制冷概念机示意图[30]

实验结果证明，以弹性体为工质，热可沿着温度梯度的反方向进行传递，在该原型机设计中，铝板与橡胶之间的润滑是较难解决的题，以石油为基础的润滑油会引起橡胶的退化；皂水可以改善性能，但干燥速度很快；石墨粉、甘油及石墨甘油混合物对性能也无明显改善作用。

李天颖[21]自主搭建了循环拉伸实验台，如图 8所示，为研究不同橡胶材料的弹热效应，实验中的橡胶材料已经消除了mullins效应。实验台主要由两部分组成：1)FLS40 系列丝杆直线模组，配有一台控制器，一台驱动和一个直流电源；2)自行设计的固定在模组上的夹具，主要材质为铝板，通过螺母加紧固定橡胶。设定速度为10 mm/s，拉伸长度为 200 mm，即应变为8。开始拉伸的同时记录温度的变化，当达到拉伸长度时，在该状态保持不变，使橡胶与环境进行自然对流和辐射换热。当温度记录仪 GP10 显示橡胶已降为环境温度时，点击归零，使橡胶按原速度返回，归零后继续记录橡胶的温度变化，直至其升温至与环境温度一致。以此循环对天然橡胶进行循环分析，得到系统温升为 5.2 ℃，理想制冷系数约为蒸气压缩制冷系统的20倍。

图8 循环拉伸实验台

C.Aprea等[68]研究了热效应在热泵中的应用，将乙酰氧基硅橡胶和硫化天然橡胶应用于活性蓄热式热泵系统，与电热材料、压热材料和磁热材料进行对比。所建立的系统如图9所示，包括：冷端换热器(与室外环境接触)、热端换热器(与室内环境接触)、由热物性材料构成的平行板蓄热器、辅助流体(水)。实验步骤包括：1)释放场，使材料回到最初状态，材料温度降低；2)辅助流体经蓄热器从热端换热器流向较冷的冷端换热器并加热蓄热器；3)施加场，材料由于热效应温度升高；4)辅助流体经蓄热器从冷端换热器流向热端换热器，水从蓄热器中吸热通过热端换热器对房间散热。

图9 活性蓄热式热泵系统

实验结果显示，乙酰氧基硅橡胶能产生的温差范围为27.3～28.8 K，硫化天然橡胶产生的温差范围为20.7～25.0 K，表明橡胶材料在固体制冷技术领域有很大的应用潜力，但与文献[21]中提到的天然橡胶的弹热效应最佳的结论有所不同。因此在后续研究中，除了开发实际弹热制冷系统，还应继续对橡胶材料本身的弹热效应加以研究，以找出弹热效应最佳的橡胶材料。

目前，以Ni-Ti合金为弹热工质的制冷系统相比以橡胶为弹热工质的制冷系统更为成熟，如下述系统模型也可应用于橡胶弹热制冷系统中。

J.Tušek等[69]发明了一种利用Ni-Ti合金作为制冷剂及蓄热器，水作为辅助流体的弹性热泵系统，通过计算系统温度跨度、比热功率和COP来评价系统性能，系统原理如图10所示。实验得到以下结论：1)在流体质量一定、流速一定、Ni-Ti质量相同的前提下，应变相同，频率越高，产生的温差越大、比热功率越大，但COP越低，因为输入功增加的速度大于比热功增加的速度；2)其他条件相同，频率一定，产生的应变越大，温度跨度越大，比热功率也越大，COP越低。

HHEX热端换热器；CHEX冷端换热器；Qin从环境吸收的热量；Qout向环境放出的热量。

4 总结与展望

4.1 总结

本文主要叙述了以橡胶为工质的弹热制冷，分别从弹热制冷效应的原理与热力学基础、橡胶的弹热效应以及应用进行叙述，并对其相关理论和研究规律进行了整理、分析与总结。

目前，对于橡胶弹热效应的理论研究已经相对成熟，但具体的制冷系统研究甚少，亟需解决的问题有：1)如何将较小拉伸-回复过程产生的制冷应用起来，这就需要研发橡胶制冷系统；2)如何提高系统的效率，这就需要研究如何提高橡胶的弹热效应。可通过向橡胶材料中添加其他材料(有待寻找)来提高弹热效应，或寻找一种方法可以使橡胶在更小的应力下发生更大的应变。

4.2 展望

自英国科学家在2004年提出将形状记忆合金应用于弹热制冷后，弹热制冷技术开始发展。橡胶具有环境友好、可回收、易制造、无毒及成本低的特点，并且与弹热效应高的Ni-Ti合金相比，有小应力产生大应变的优点，未来绿色环保的固态制冷技术必将取代对环境污染严重的蒸气压缩制冷技术，而橡胶是很有潜力的弹热工质之一。但目前为止，有关天然橡胶的研究还处于初始阶段，未来的发展十分光明。有关橡胶弹热制冷未来的发展方向有：优化橡胶制冷体系，探索新的橡胶制冷体系，开发具有高疲劳寿命、高导热系数特性的橡胶材料等。

弹热制冷技术最有望代替传统压缩式制冷技术，因此，弹热制冷技术在今后得到更快、更广泛的发展需要我国能源、材料领域的学者和相关企业能够积极参与到该项技术的研究和开发工作中，为我国制冷、空调行业的节能减排、环保等工作作出贡献。

符号说明

T——温度， K

s——比熵， J/(kg·K)

l——长度， m

γ——弹热系数， J/(K·m)

RC——制冷剂容量， W

h——表面传热系数， W/(m2·K)

A——橡胶传热的表面积， m2

Text——环境温度， K

t——时间， s

c——比热容， J/(kg·K)